Как найти частоту свободных колебаний в контуре

Колебательный контур LC

Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.

Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.

– Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
– Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.

Рассмотрим, как возникают и поддерживаются свободные электрические колебания в параллельном контуре LC.

Основные свойства индуктивности

– Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией .
– Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.

Природа электромагнитных колебаний в контуре

Период свободных колебаний контура LC можно описать следующим образом:

Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток разряда конденсатора, создавая магнитное поле в катушке.

Внешний магнитный поток создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в каждом витке, поэтому конденсатор разрядится не мгновенно, а через время t₁,
которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t₁ = .
По истечении времени t₁, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, E_C будет равна E_L.
Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Далее изменение (уменьшение от максимума) магнитного потока накопленной энергии катушки будет создавать в ней ЭДС,
которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t₂ = t₁, он перезарядит конденсатор от нулевого до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.

Описанные интервалы t₁ и t₂ составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление.
Магнитная энергия вновь будет накапливаться в катушке в течении времени t₃, сменив полярность полюсов.

В течении заключительного этапа колебания (t₄),
накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U
(в случае отсутствия потерь) и процесс колебания повторится.

В реальности, при наличии потерь энергии на активном сопротивлении проводников,
фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t₁ + t₂ + t₃ + t₄ составит период колебаний .
Частота свободных колебаний контура ƒ = 1 / T

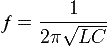
Частота свободных колебаний является частотой резонанса контура,
на которой реактивное сопротивление индуктивности X_L=2πfL равно реактивному сопротивлению ёмкости X_C=1/(2πfC).

---

Расчёт частоты резонанса LC-контура:

Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

---

Похожие страницы с расчётами:

Рассчитать импеданс.

Рассчитать реактивное сопротивление.

Рассчитать реактивную мощность и компенсацию.

---

23.07.2012

АМПЛИТУДА И ЧАСТОТА СВОБОДНЫХ КОЛЕБАНИЙ В КОНТУРЕ

Амплитуды напряжения и тока свободных электрических колебаний в данном контуре зависят от начального запаса энергии. Чем больше напряжение первоначального заряда конденсатора контура, тем больше амплитуда колебаний.

Каждый контур имеет определенную частоту происходящих в нем свободных колебаний. Она называется собственной частотой контура или, просто, частотой контура Fo и зависит от емкости и индуктивности контура. Чем больше индуктивность и емкость, тем больше период свободных колебаний и тем меньше их частота.

Если емкость увеличить, то время заряда и разряда конденсатора станет больше, так как при прежнем напряжении количество электричества в конденсаторе будет больше. Увеличение индуктивности, в свою очередь, вызовет более медленное нарастание и спадание тока при разряде и заряде конденсатора, так как большая индуктивность сильнее препятствует изменениям тока. Значит, колебания будут происходить медленнее, т.е. частота уменьшится. При уменьшении L и С колебания, наоборот, совершаются быстрее и, следовательно, частота увеличивается.

Чтобы уменьшить частоту контура в 2 раза, нужно увеличить в 4 раза емкость или индуктивность контура. Можно, однако, увеличить емкость в 2 раза,, но одновременно увеличить и. индуктивность также в 2 раза. Чтобы изменить частоту в 3 раза, нужно изменить L или С, или их произведение в 9 раз и т.д.
Одну и ту же частоту можно получить при разных значениях емкости и индуктивности; важно только, чтобы их произведение L*C было неизменно.

Длина радиоволн обратно пропорциональна частоте. Поэтому с уменьшением емкости и индуктивности длина волны контура (ламбда) уменьшается, а при увеличении С и L она увеличивается.

На (рис.1) показаны графики зависимости частоты контура Fo и соответствующей длины волны ? от емкости или индуктивности, называемые кривыми, или графиками настройки контура.

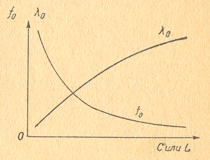
Рис.1 — График настройки контура

Зависимость частоты контура от его емкости и индуктивности выражается формулой Томсона

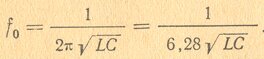
Здесь Fо выражена в герцах, a L и С — в генри и фарадах. Английский ученый Томсон впервые дал эту формулу для периода свободных колебаний в контуре

Но в радиотехнике пользуются величиной частоты, так как период составляет малую долю секунды, что неудобно.

Формула Томсона легко выводится из равенства индуктивного и емкостного сопротивлений при свободных колебаниях

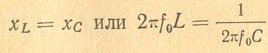
Из этого вытекает, что

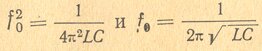
В любой колебательной системе частота свободных колебаний зависит от двух параметров. У колебательного контура эти параметры — индуктивность и емкость — можно легко изменять. Для обычного маятника один параметр — длину его — также можно изменять. Нетрудно показать, что для изменения частоты в 2 раза длину надо изменить в 4 раза, для изменения частоты в 3 раза длина маятника должна быть изменена в 9 раз и т. д. Вторым параметром у маятника является ускорение, создаваемое земным тяготением. Эта величина равна         g = 9,81 м/сек2 и ее нельзя изменить по нашему желанию.

Лучшей механической аналогией колебательного контура является пружинный маятник (рис.2).

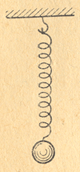
Рис.2 — Пружинный маятник

Частота его свободных колебаний зависит от веса (или массы) грузика и гибкости пружины. Гибкость является величиной, обратной упругости, и характеризует податливость пружины к растяжению или сжатию под влиянием приложенной силы. Величина гибкости зависит от толщины и материала проволоки пружины, диаметра ее витков и их числа. Если увеличить число витков в 4 раза, то во столько же раз увеличится гибкость, а частота колебаний уменьшится в 2 раза. Такое же изменение частоты получится, если увеличить в 4 раза вес грузика. Поэтому с данным маятником легко показать зависимость частоты свободных колебаний от двух параметров.

Поделиться с друзьями:

Твитнуть

Поделиться

Плюсануть

Поделиться

Отправить

Класснуть

Линкануть

Запинить

В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания.

Электромагнитными колебаниями называют периодические взаимосвязанные изменения заряда, силы тока и напряжения.

Свободными колебаниями называют такие, которые совершаются без внешнего воздействия за счет первоначально накопленной энергии.

Вынужденными называются колебания в цепи под действием внешней периодической электродвижущей силы

Свободные электромагнитные колебания – это периодически повторяющиеся изменения электромагнитных величин (q – электрический заряд, I – сила тока, U – разность потенциалов), происходящие без потребления энергии от внешних источников. 

Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур или колебательный контур.

Колебательный контур – это система, состоящая из последовательно соединенных конденсатора емкости C, катушки индуктивности L и проводника с сопротивлением R 

Рассмотрим закрытый колебательный контур, состоящий из индуктивности L и емкости С.

 

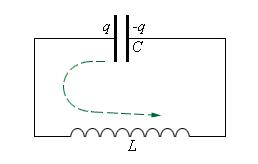
Чтобы возбудить колебания в этом контуре, необходимо сообщить конденсатору некоторый заряд от источника ε. Когда ключ K находится в положении 1, конденсатор заряжается до напряжения . После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер

 

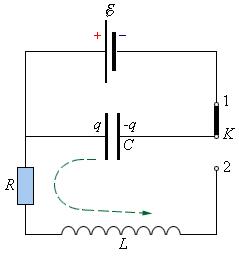
Свободные электромагнитные колебания можно наблюдать на экране осциллографа.

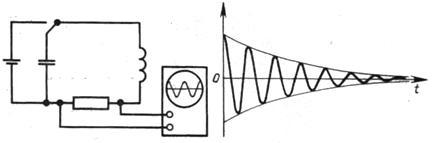
Как видно из графика колебаний, полученного на осцилографе, свободные электромагнитные колебания являются затухающими, т.е.их амплитуда уменьшается с течением времени. Это происходит потому, что часть электрической энергии на активном сопротивлении R превращается во внутреннюю энерги. проводника (проводник нагревается при прохождении по нему электрического тока).

Рассмотрим, как происходят колебания в колебательном контуре и какие изменения энергии при этом происходят. Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0).

Если зарядить конденсатор до напряжения U₀ то в начальный момент времени t₁=0 на обкладках конденсатора установятся амплитудные значения напряжения U₀ и заряда q₀ = CU₀.

Полная энергия W системы равна энергии электрического поля W_эл:

Если цепь замыкают, то начинает течь ток. В контуре возникает э.д.с. самоиндукции

Вследствие самоиндукции в катушке конденсатор разряжается не мгновенно, а постепенно (так как, согламно правилу Ленца, возникающий индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван. Т.е. магнитное поле индукционного тока не дает мгновенно увеличиться магнитному потоку тока в контуре). При этом ток увеличивается постепенно, достигая своего максимального значения I₀ в момент времени t₂=T/4, а заряд на конденсаторе становится равным нулю.

По мере разрядки конденсатора энергия электрического поля уменьшается, но одновременно возрастает энергия магнитного поля. Полная энергия контура после разрядки конденсатора равна энергии магнитного поля W_м:

В следующий момент времени ток течет в том же направлении, уменьшаясь до нуля, что вызывает перезарядку конденсатора. Ток не прекращается мгновенно после разрядки конденсатора вследствии самоиндукции (теперь магнитное поле индукционного тока не дает магнитному потоку тока в контуре мгновенно уменьшиться). В момент времени t₃=T/2 заряд конденсатора опять максимален и равен первоначальному заряду q = q₀, напряжение тоже равно первоначальному U = U₀, а ток в контуре равен нулю I = 0.

Затем конденсатор снова разряжается, ток через индуктивность течёт в обратном направлении. Через промежуток времени Т система приходит в исходное состояние. Завершается полное колебание, процесс повторяется.

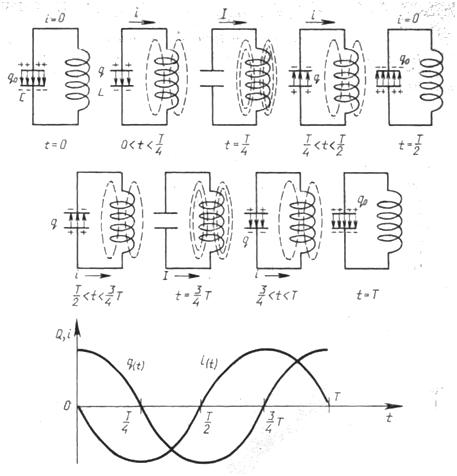
График изменения заряда и силы тока при свободных электромагнитных колебаниях в контуре показывает, что колебания силы тока отстают от колебаний заряда на π/2.

В любой момент времени полная энергия:

При свободных колебаниях происходит периодическое превращение электрической энергии W_э, запасенной в конденсаторе, в магнитную энергию W_м катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается постоянной.

Свободные электрические колебания аналогичны механическим колебаниям. На рисунке приведены графики изменения заряда q(t) конденсатора и смещения x(t) груза от положения равновесия, а также графики тока I(t) и скорости груза υ(t) за один период колебаний.

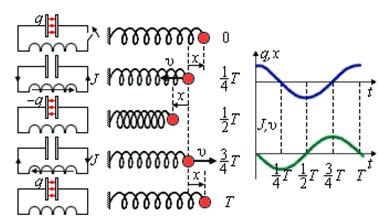
В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону

q(t) = q₀cos(ωt + φ₀)

Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний  и период колебаний  – формула Томпсона

Амплитуда q₀ и начальная фаза φ₀ определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия.

Для колебаний заряда, напряжения и силы тока получаются формулы:

Для конденсатора:

q(t) = q₀cosω₀t

U(t) = U₀cosω₀t

Для катушки индуктивности:

i(t) = I₀cos(ω₀t + π/2)

U(t) = U₀cos(ω₀t + π)

Вспомомним основные характеристики колебательного движения:

q_0, U₀, I₀ – амплитуда – модуль наибольшего значения колеблющейся величины

Т – период – минимальный промежуток времени через который процесс полностью повторяется

ν – Частота – число колебаний в единицу времени

ω – Циклическая частота – число колебаний за 2п секунд

φ – фаза колебаний – величина стоящая под знаком косинуса (синуса) и характеризующая состояние системы в любой момент времени.