Как найти число поворотов

Как найти число поворотов

Студворк — интернет-сервис помощи студентам

В конструкторском бюро проектируют планетоход для исследования поверхности планеты Марс. Исследования должны проводиться на прямоугольной области планеты без препятствий внутри неё. Эта область разделена на единичные квадраты и имеет размеры M и N, где M – длина прямоугольника, а N – его ширина.

Планируется, что планетоход должен работать по следующей программе. Вначале он садится в северо-западном углу заданной области в направлении на восток. После этого планетоход начинает обход и исследование выбранной области, двигаясь по спирали по часовой стрелке. При этом спираль постепенно “Закручивается” вовнутрь, захватывая постепенно все клетки прямоугольника. Исследование заканчивается, когда пройдены все клетки.

Требуется написать программу, которая для заданных M и N определяет кол-во поворотов, которые должен выполнить планетоход в процессе исследования области.

Пример: M = 3, N=4. Кол-во поворотов = 3.

Как можно решить?

Источник

I found my mistake! Posting it as an answer, so future viewers can see what is happening. The issue was not the computation, but misuse of a formula. The thing is that the formula I wanted to use for the turning number, i.e.

$$n_{beta} = frac{1}{2pi} int_{0}^{L} K_{beta}(t)dt$$

may only be used for curves that are parametrized by arclength. Since curvature is invariant under reparametrization I just assumed that it would work the same way. But the reparametrization-invariance actually gives us

$$K_{beta circ varphi}(t) = K_{beta}(varphi(t)),$$

where $beta circ varphi$ is a reparametrization of $beta$ by arclength. So what I ignored was the $varphi(t)$ as the argument of the curvature. If we account for this, by a change of variable we get

$$n_{beta} = frac{1}{2pi} int_{0}^{L} K_{beta}(varphi(t)), dt = frac{1}{2pi} int_{0}^{L} K_{beta}(t)cdot|varphi'(t)|,dt = frac{1}{2pi} int_{0}^{L} K_{beta}(t)cdot||dot{beta}(t)||,dt,$$

where for the last equality we used the fact that the reparametrization is given by $varphi(s) = int_{s_0}^{s} ||dot{beta}(tau)||,dtau$, so $varphi'(s) = ||dot{beta}(s)||$ by the fundamental theorem of calculus. Therefore, in my exercise one must integrate the function

$$K_{beta}(t)cdot||dot{beta}(t)|| = frac{-6cos t-9}{4cos t + 5}$$

which evaluates to $-4pi$, giving the turning number of -2, which is exactly what it should be.

Источник

Число оборотов (также называется числом оборотов или индекса ) является топологическим инвариантом , который играет решающую роль в теории функций .

Предварительный просмотр

Число оборотов кривой по отношению к точке представляет собой количество оборотов против часовой стрелки при следовании по кривой. Поворот по часовой стрелке дает отрицательное число оборотов -1.
гамма z_ {0}z_ {0}

Количество ходов

1 −1 0 1 2
Количество витков = 1 (обвести против часовой стрелки) Количество витков = −1 Количество витков = 0 Количество витков = 1 Количество витков = 2

определение

Если замкнутая кривая находится внутри и если есть точка , на которой не лежит, то число оборотов определяется в зависимости от :
гамма mathbb {C} z_ {0} mathbb C,гамма гамма z_ {0}

{ displaystyle operatorname {ind} _ { gamma} (z_ {0}) = n ( gamma, z_ {0}): = { frac {1} {2 pi mathrm {i}}} int _ { gamma} { frac { mathrm {d} zeta} { zeta -z_ {0}}}}

Номер тиража (согласно английскому индексу ) часто обозначается в литературе как или . Число оборотов замкнутой кривой всегда целое число независимо от контрольной точки.
operatorname {ind}Я. чи

расчет

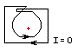
Количество витков можно определить интуитивно с помощью

operatorname {ind} _ gamma (z_0) =Число оборотов от мкм против часовой стрелки – число оборотов от мкм по часовой стрелкегамма z_ {0}гамма z_ {0}

вычислять. Расчет с помощью определения часто бывает нелегко. В качестве примера выберем единичный круг

{ displaystyle gamma двоеточие [0,2 pi] to mathbb {C}, , t mapsto e ^ { mathrm {i} t}}

как кривая. Согласно интуитивному правилу, это для всех точек внутри и для всех точек вне замкнутого кругового диска . Последнее непосредственно следует из интегральной теоремы Коши и определения. Будь сейчас
operatorname {ind} _ gamma (z) = 1г в mathbb E mathbb E operatorname {ind} _ gamma (z) = 0{ displaystyle z in mathbb {C} setminus { bar { mathbb {E}}}}{ displaystyle { bar { mathbb {E}}}}

{ displaystyle f двоеточие mathbb {E} to mathbb {C}, , z mapsto operatorname {ind} _ { gamma} (z).}

Это относится

operatorname {ind} _ gamma (0) = f (0) = frac 1 {2 pi mathrm i} int_ gamma frac { mathrm d zeta} zeta = frac 1 {2 pi mathrm i} int limits_0 ^ {2 pi} frac { mathrm ie ^ { mathrm it}} {e ^ { mathrm it}} mathrm dt = 1.

Замена дифференциации и интеграции приводит к

{ displaystyle f '(z) = { frac {1} {2 pi mathrm {i}}} int _ { gamma} { frac { mathrm {d} zeta} { left ( zeta -z right) ^ {2}}}}

и поскольку примитив подынтегрального выражения есть, потому что когерентно есть, поэтому для всех zeta mapsto - frac 1 { zeta-z}е ' эквив 0. mathbb E f (z) = operatorname {ind} _ gamma (z) = 1z in mathbb E.

Применение в теории функций

Число оборотов в основном используется при вычислении интегралов кривой на плоскости комплексных чисел. Быть

{ Displaystyle е двоеточие mathbb {C} setminus left {a_ {1}, dotsc, a_ {n} right } to mathbb {C}}

мероморфны функция с особенностями , то можно после теоремы вычетов , интеграл от а ( с помощью любого из особенностей , простирающихся) кривой с помощью
{ displaystyle a_ {1}, dotsc, a_ {n},}жгамма

{ displaystyle int _ { gamma} f mathrm {d} z = 2 pi mathrm {i} sum _ {k = 1} ^ {n} operatorname {ind} _ { gamma} (a_ {k}) operatorname {Res} _ {a_ {k}} f}

вычислять.

алгоритм

Количество поворотов поверхностей нетривиального многоугольника: количество поворотов поверхности, на которой расположена точка, равно -1, т. Е. Это означает, что он находится внутри многоугольника (серая область). Каждая поверхность имеет фиксированное количество витков.

В алгоритмической геометрии число оборотов используется для определения, находится ли точка вне или внутри непростого многоугольника (многоугольника, края которого пересекаются). Для простых многоугольников алгоритм четно-нечетного правила упрощен.

Для многоугольников (замкнутых ребер) используется следующий алгоритм для расчета количества оборотов:

  1. Найдите половинную линию (начинающуюся от исследуемой точки снаружи ), которая не содержит угловых точек многоугольника.
  2. Набор ш = 0.
  3. Для всех пересечений полуоси с многоугольником:
  4. ш теперь количество оборотов точки.

Если число вращения равно 0, точка находится вне многоугольника, в противном случае – внутри.

В примере напротив, первая линия, начинающаяся с вертикальной стрелки. Он обрезает три стороны многоугольника. Что касается красного края, то точка находится справа. Что касается следующего края, то точка также находится справа, а в отношении последнего края точка находится слева. Точка находится внутри многоугольника. Область многоугольника имеет серый фон.
{ Displaystyle влево (ш = -1 вправо).}{ Displaystyle влево (ш = -2 вправо)}{ Displaystyle влево (ш = -1 вправо).}

Аналогичный алгоритм также дает количество оборотов вокруг одной точки для непрямых (замкнутых) кривых, но проверить точки пересечения там не так просто.

Обобщение на n -мерные многообразия

Обобщение на n – мерных многообразия приходит от Николая Nikolajewitsch Боголюбов : Используя теорему общего Стокса для одной банки
пz_0 = 0

mathrm {ind} _ { gamma} (0) = frac {1} {n mathrm {Vol (B)}} oint _ { gamma} frac { vec x cdot mathrm d vec S } { | х | ^ {п}}

написать. – единичная сфера; im – рассматриваемое -мерное замкнутое многообразие, на котором нужно интегрировать.
Б. mathbb R ^ n, гамма (п-1)

Смотри тоже

  • Интегральная формула Коши
  • Остаточная теорема
  • Кривая интеграла

литература

  • Эберхард Фрайтаг, Рольф Бусам: Теория функций 1. Springer-Verlag, Berlin, ISBN 3-540-67641-4 .
Источник

Формулировка задачи:

Маршрут движения автомобиля задан в виде координат вершин ломаной. Необходимо определить количество левых поворотов. Осуществить графическое изображение ломаной. Программа должна считывать координаты вершин из файла, который имеет текстовую структуру; координаты записаны в одну строку через запятые и без пропусков.

Код к задаче: «Определить количество левых поворотов автомобиля»

textual

d:=(x3-x1)*(y2-y1)-(y3-y1)*(x2-x1);
if d=0 then write('нет поворота')
else if d<0 then write('налево')
else write('направо')

Полезно ли:

15   голосов , оценка 3.933 из 5

Источник

Добавить комментарий