Как найти дисперсию методом моментов

«Способ
моментов» основан на математических
свойствах дисперсии. Для рядов
распределения с равными интервалами
расчет дисперсии можно произвести по
следующей формуле:

,

где
i – размер интервала;

m₁
– момент первого порядка

(х₁
– упрощенные варианты;
);

m₂
– момент второго порядка
.

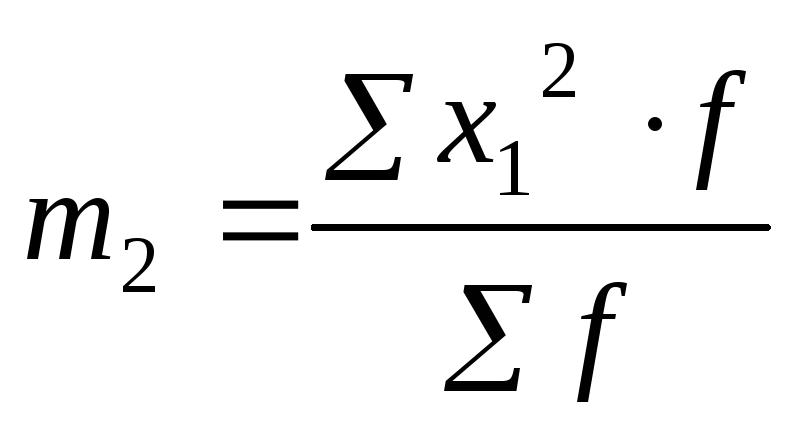Рассмотрим
применение «способа моментов» в расчете
дисперсии и среднеквадратического
отклонения на примере следующих данных.

Пример 2. Расчет
дисперсии и среднего квадратического
отклонения необходимо провести по
данным условия предыдущей задачи.
Расчеты следует оформить в табл. 20.

Таблица 20

Группировка работающих по возрасту, лет (х)	Удельный вес работающих, % ( f )	Середина интервала (х)	х – А
До 20	4	15	–20	–2	–8	4	16
20–30	20	25	–10	–1	–20	1	20
30–40	30	35	0	0	0	0	0
40–50	28	45	10	1	28	1	28
Свыше 50	18	55	20	2	36	4	72
Итого	100	–	–	–	36	–	136

Размер
интервала i
= 10, А
= 35 (варианта с наибольшей частотой):

;

;

;

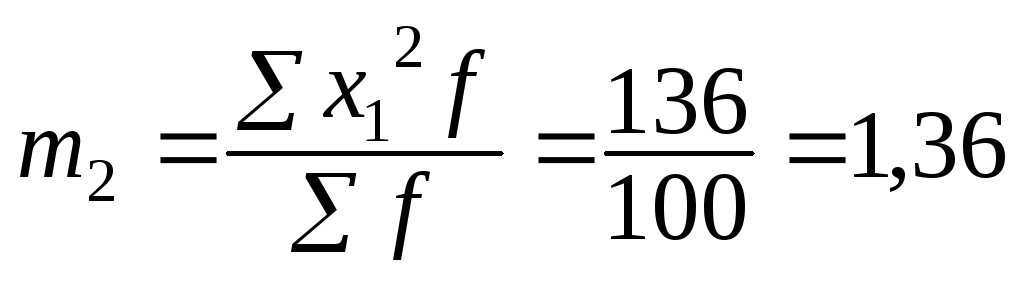лет.

Признаки,
которыми обладают одни единицы
совокупности и не обладают
другие, называются альтернативными.
Вариацию качественных
признаков можно определить, рассчитав
дисперсию альтернативного признака
(дисперсию доли) по формуле

,

где р
– доля единиц, обладающих изучаемым
признаком;

q– доля единиц,
не обладающих этим признаком.

В связи
с тем, что p
+ q
= 1, то q
= 1 – p,
следовательно,
.

Определим вариацию
качественного признака в следующем
примере.

Пример
3.
Имеются следующие данные по Республике
Беларусь (на конец
1998 г.): всего заняты в народном хозяйстве
– 4416,6 тыс. чел., из них имеют высшее
образование – 870,1 тыс. чел.

Необходимо
определить дисперсию и среднее
квадратическое отклонение доли занятых
в народном хозяйстве и имеющих высшее
образование.

Решение

Рассчитаем дисперсию
альтернативного признака по формуле

,

где р
– доля единиц, обладающих интересующим
нас признаком.

Произведем следующие
расчеты:

;

;

.

Исчислим среднее
квадратическое отклонение следующим
образом:

.

6.3. Внутригрупповая и межгрупповая вариации

Вариация признака
определяется различными факторами.

Вариация,
обусловленная влиянием фактора,
положенного в основу группировки,
называется межгрупповой вариацией и
характеризуется межгрупповой дисперсией
(²).

Межгрупповая
дисперсия является мерой колеблемости
частных (групповых) средних

около общей средней

и исчисляется по формуле

,

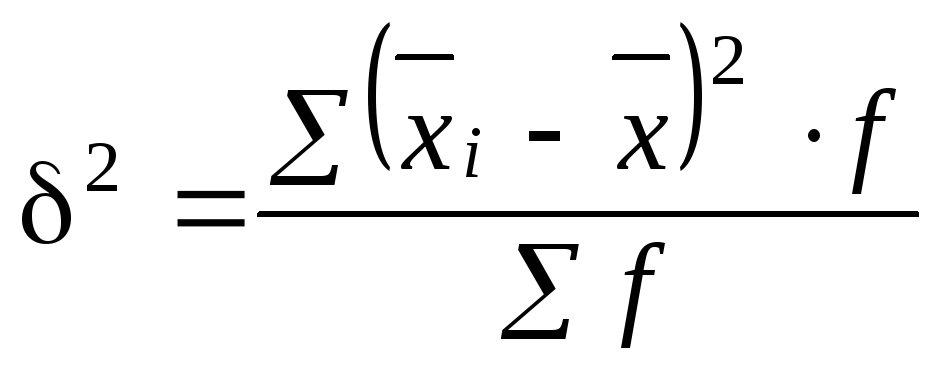где f
– количество единиц совокупности в
каждой i-й
группе.

Вариацию,
обусловленную влиянием прочих факторов,
характеризует в каждой группе
внутригрупповая дисперсия
,
которую определяют по следующей формуле:

.

Средняя
из внутригрупповых, или частных дисперсий
определяется по формуле средней
арифметической взвешенной дисперсий
групп

.

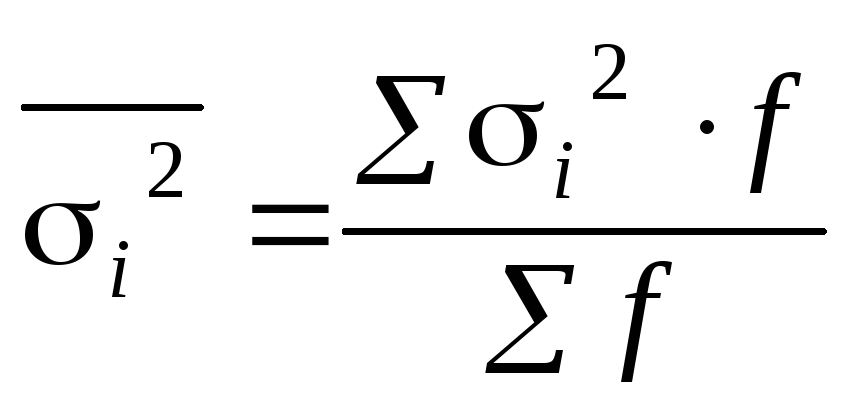Общая дисперсия
признака равна сумме межгрупповой и
средней арифметической внутригрупповых
дисперсий:

.

Отношение
межгрупповой дисперсии к общей дает
коэффициент детерминации (²).
Данный коэффициент характеризует, какая
доля всей вариации признака обусловлена
признаком, положенным в основание
группировки:

.

Корень квадратный
из коэффициента детерминации дает
эмпирическое корреляционное отношение,
которое характеризует тесноту связи
между группировочным и результативным
признаками:

.

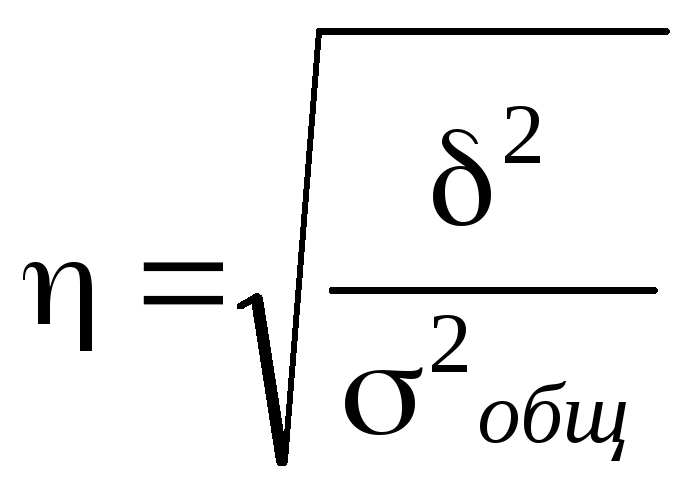Этот показатель
изменяется от 0 до 1.

Определим
перечисленные выше показатели.

Пример
4.
Расчеты σ²_общ
необходимо провести по данным примера
1, рассматриваемого
в теме 3 (см. сводную групповую табл. 3).

Расчет межгрупповой
дисперсии следует произвести по формуле

.

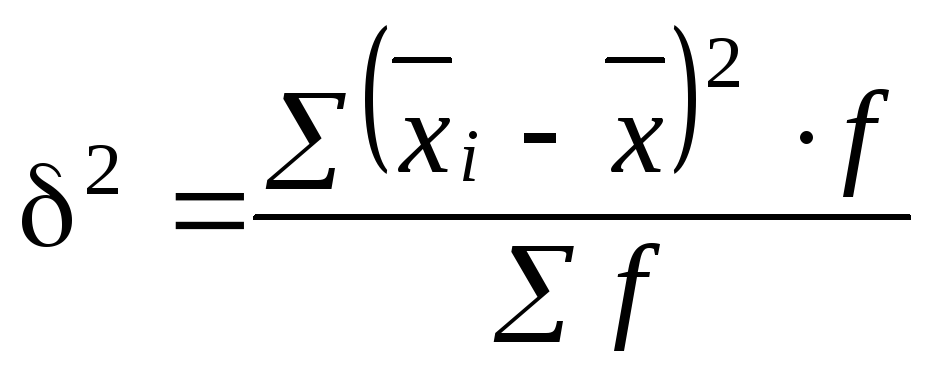Вспомогательные
расчеты необходимо оформить в табл. 21.

Таблица 21

	f
527,5	9	–238,7	56977,69	512799,21
741,3	3	–24,9	620,01	1860,03
969,7	6	203,5	41412,25	248473,5
1266,8	2	500,6	250600,36	501200,72
Итого	20	–	–	1264333,46

= 766,2 млн р.

δ²
= 1264333,46 : 20 = 63216,67.

Среднюю из
внутригрупповых дисперсий рассчитаем
по формуле

,

где
.

Воспользуемся
упрощенным способом расчета:

.

Расчеты по 1-й
группе проводим на основании данных
табл. 2. Результаты расчетов заносим в
табл. 22.

Таблица 22

х	х2
578,8	335009,44
435,4	189573,16
527,6	278361,76
578,0	334084,0
532,0	283024,0
605,6	366751,36
394,0	155236,0
516,0	266256,0
580,0	336400,0
 4747,4	 2544695,72

= 282743,97 – 278256,25 =
4487,72.

Расчеты по 2-й
группе произведем согласно данным табл.
2. Результаты расчетов запишем в табл.
23.

Таблица 23

х	х2
620,8	385392,64
822,4	676341,76
780,8	609648,64
 2224,0	 1671383,04

= 557127,68 – 549525,69 =
7601,99.

Расчеты по 3-й
группе произведем исходя из данных
табл. 2. Результаты расчетов заносим в
табл. 24.

Таблица 24

х	х2
1047,2	1096627,84
930,8	866388,64
980,0	960400,0
944,4	891891,36
894,0	799236,0
1021,6	1043666,56
 5818,0	 5658210,4

= 943035,07 – 940259,91 =
2775,16.

Расчеты по 4-й
группе произведем согласно данным табл.
2. Результаты расчетов заносим в табл.
25.

Таблица 25

х	х2
1279,2	1636352,64
1254,4	1573519,3
 2533,6	 3209872,0

= 1604936,0 – 1604782,24 =
153,76.

Затем
рассчитаем среднюю внутригрупповую
дисперсию по формуле

.

Общая дисперсия
признака равна:

.

Определим коэффициент
детерминации следующим образом:

(94
%).

Следовательно, 94
% всей вариации издержек обращения
обусловлены вариацией товарооборота.

Эмпирическое
корреляционное отношение равняется:

Таким образом,
взаимосвязь между признаками тесная.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

7.2. Свойства дисперсии, расчет дисперсии способом моментов

Дисперсия обладает рядом математических свойств. Приведем основные из них:

1. если x_i = c, где с – постоянная величина, то дисперсия будет равна нулю;
2. если из всех значений признака вычесть постоянную величину с, то дисперсия от этого не изменится:

   

3. если все индивидуальные значения признака уменьшить в d раз, то дисперсия уменьшится в d² раз:

   

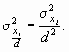
На приведенных свойствах дисперсии основан один из методов ее расчета – способ моментов. Согласно ему, дисперсию можно вычислить по следующей формуле (применяется только в случае вариационных рядов с равными интервалами):

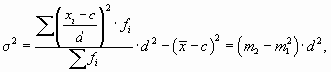
где с – значение середины интервала, находящегося в центре ряда (если количество интервалов четное, то берется середина интервала из центра ряда с наибольшей частотой);

d – величина интервалов;

– момент второго порядка;

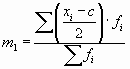– момент первого порядка.

По данным табл. 7.5 определим дисперсию способом моментов.

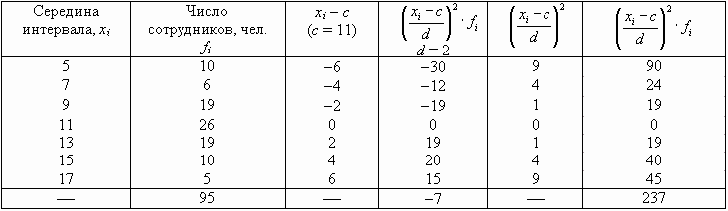
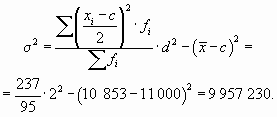
или

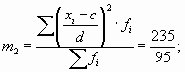
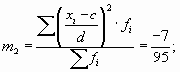
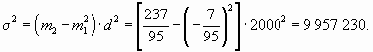
Если при расчете дисперсии способом моментов взять за постоянную величину с нуль, а за d – единицу, то приведенная выше формула примет следующий вид:

Таким образом получаем, что дисперсия равна разности между средней из квадратов индивидуальных значений признака и квадрата средней.

Применим данный способ расчета дисперсии. Пусть известно, что средняя арифметическая величина, рассчитанная для вариационного ряда, равна 56 дол., а средний квадрат его индивидуальных значений – 3322. Определим дисперсию.

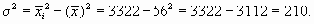
Сегодня поговорим о математической статистике и теории вероятностей. Затронем немного один из типов задач по теме моментов.

О сути метода

Метод моментов — это метод оценки неизвестных параметров распределения случайной величины в математической статистике. Суть метода заключается в следующем. У нас есть некоторые реальные данные распределения. К этим данным мы подбираем теоретическое распределение. Под этим подразумевается некоторая функция плотности вероятностей. Естественно, эта функция имеет какие-то неизвестные (чаще всего от 1 до 3). И чтобы найти эти неизвестные, мы считаем числовые характеристики (моменты) теоретического распределения, то есть математическое ожидание, дисперсию. Затем мы сопоставляем посчитанные параметры по реальным данным с теоретическими параметрами для конкретного распределения. В итоге получаем систему уравнений относительно неизвестных параметров распределения. Решая систему, находим эти параметры.

Что же за характеристики, которые представляются этими моментами?

Моменты случайной величины — это некоторые функции, которые численно описывают характеристики распределения данной случайной величины. Существуют начальные, центральные, абсолютные, центрально абсолютные и факториальные моменты.

На практике чаще всего используются четыре первых момента.
Первый момент соответствует математическому ожиданию случайной величины, он показывает относительное расположение распределения на числовой прямой.
Второй момент соответствует дисперсии распределения, он показывает разброс вокруг среднего значения (то есть вокруг математического ожидания или первого момента).
Третий момент при нормализации (то есть момент, деленный на среднее квадратичное отклонение в кубе) является числовой характеристикой симметрии распределения. Еще называется коэффициентом асимметрии.
Четвертый момент соответствует коэффициенту эксцесса распределения, он показывает меру тяжести краев распределения или же меру остроты пика.

Моменты можно вычислить по общей формуле:

В большинстве задач используются первый и второй моменты. То есть математическое ожидание и дисперсия.

Немного абстрактный пример задачи

Случайная величина ξ равна сумме двух независимых случайных величин, имеющих показательное распределение с параметрами λ₁ и λ₂ соответственно. По наблюдениям случайной величины ξ оценить параметры λ₁ и λ₂ методом моментов в предположении что λ₁ > λ₂

Решение:

Допустим, у нас есть две случайные величины, распределенные по показательному закону:

Найдем закон распределения для их суммы: Z = X + Y.
Пусть f(x, y) – плотность совместного распределения случайных величин X и Y. Функция распределения случайной величины Z определяется соотношением:

Двойной интеграл можно записать в виде:

Так как плотность распределения :

то, дифференцируя внутренний интеграл по z как интеграл с переменным верхним пределом, получим формулу плотности распределения:

Если случайные величины X и Y не зависят друг от друга, то плотность совместного их распределения равна произведению плотностей распределения каждой, поэтому:

Получаем:

По свойствам математического ожидания:

Проверим напрямую:

Дисперсия случайной величины в показательном законе распределения определяется формулой

В случае, если речь идет о сумме двух случайных величин, то получаем:

Зная первый и второй моменты, мы можем найти параметры λ₁ и λ₂ из системы уравнений:

Показательное распределение применяют в теории массового обслуживания и надёжности, для моделирования времени безотказной работы, длительности безаварийной работы приборов и машин, демографии. Различные распределения изучаются на факультетах логистики и транспорта (в том числе и магистры вузов Европы) в контексте надежности распределительных систем.

Задачка для тренировки читателя

Случайная величина X – время работы лампы накаливания.  Случайная величина подчинена показательному распределению. Определить вероятность того, что время работы лампы накаливания будет не меньше 800 часов, если среднее время работы лампы накаливания 400 часов.

Попробуйте решить на черновике и напишите свой ответ в комментарии.

Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK

Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram