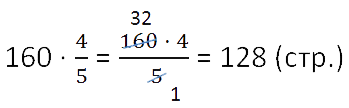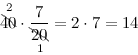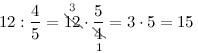Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Нахождение дроби от числа
Поддержать сайт
Дроби используют в математике, чтобы кратко обозначить часть
рассматриваемой величины.
Но если есть часть, то обязательно есть и целое (то, отчего
была взята эта часть).
Зная целое, можно найти его часть, указанную соответствующей дробью.
Запомните!
Чтобы найти дробь (часть) от числа, нужно это число
умножить на данную дробь.
Пример. Рассмотрим задачу.
В книге 160 страниц. Юра прочитал
книги. Сколько страниц
прочитал Юра?
Прежде всего найдём в задаче целое. Это — вся книга и в ней всего
160 страниц.
Посмотрим на дробь (часть) от целого:
.
Знаменатель равен 5, значит, целое разделили
на 5 частей и мы можем найти сколько страниц составляет
часть.
- 160 : 5 = 32 (стр.) — составляет часть страниц.
- Числитель дроби равен 4, значит взято 4 части.
- 32 · 4 = 128 (стр.) — составляют книги.
Оба действия можно записать кратко, в соответствии с правилом нахождения части от целого.
Ответ: Юра прочитал 128 страниц.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
В данной публикации мы рассмотрим, каким образом можно найти дробь от целого числа и наоборот – как найти число, если известно, чему равна определенная дробь от него. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Нахождение дроби от числа
- Нахождение числа по значению дроби
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅
a/b
=
n ⋅ a/b
Пример 1
Решение
5/12
⋅ 24 =
5 ⋅ 24/12
=
120/12
= 10
Пример 2
Решение
4/9
⋅ 7 =
4 ⋅ 7/9
=
28/9
=3
1/9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет
2/5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :
2/5
= 20 ⋅
5/2
=
20 ⋅ 5/2
= 50
Лучший ответ
Елена Кухарева
Профи
(904)
13 лет назад
умножить число (или дробь) на эту дробь. Например 1/3 от 27 это 27*1/3=9 или 1/2 от 2/3, это 2/3*1/2=2/6
Остальные ответы
Кира
Ученик
(151)
13 лет назад
Чтобы найти дробь от числа, надо эту дробь умножить на число. 2.Чтобы найти число по его дроби, надо это число разделить на данную дробь.
Mari
Мастер
(1036)
13 лет назад
Чтобы найти дробь от числа нужно умножить число на эту дробь.
вишня ярмоловна
Ученик
(153)
7 лет назад
Чтобы найти дробь (часть) от числа, нужно это число умножить на данную дробь
Источник: голова и учебник
Алексей Волков
Ученик
(148)
7 лет назад
чтобы найти дробь от числа надо число умножить на верхнее число а на нижние разделить
Макс Миленин
Ученик
(109)
7 лет назад
мда
Иван Пушнаренко
Ученик
(139)
7 лет назад
сколько пятых долей 2целых двух пятых
Ульяна Павлова
Знаток
(403)
6 лет назад
а как найти дробь от дроби?
виталий герасимов
Знаток
(287)
6 лет назад
про батя
Вика Рейн
Ученик
(114)
6 лет назад
как
Существует ряд задач, в которых необходимо найти часть или дробь
некоторого числа. Такие задачи решаются умножением на основании следующего правила:
Чтобы найти дробь от заданного числа, нужно это число умножить на дробь.
Пример
Задание. Найти
$frac{7}{20}$ от 40.
Решение. В рассматриваемом примере 40 – это заданное число, $frac{7}{20}$ – дробь, задающая искомую часть.
Тогда, согласно правилу, имеем:
Итак, получили, что $frac{7}{20}$ от 40 равно 14 – искомая часть данного числа.
Ответ. $frac{7}{20}$ от 40 равно 14.
Иногда требуется по известной части числа и дроби, которая выражает эту часть, определить все число. Подобные задачи решаются делением.
Чтобы найти число, по известной величине его дроби, надо заданную величину поделить на дробь.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В классе 12 мальчиков, что составляет $frac{4}{5}$ части всех учеников класса.
Сколько всего человек учится в классе?
Решение. Искомое количество учеников
Ответ. Всего в классе учится 15 человек.
Читать следующую тему: десятичные дроби.
- Категория: Математика
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби и умножить на числитель. Чтобы найти число по его дроби, нужно число разделить на числитель и умножить на знаменатель.
Разберем на примере задачи нахождение дроби от числа.
От дома до школы 560 м. Саша прошел 2/5 этого пути. Сколько метров прошел Саша?
Весь путь – это 5 частей или одно целое (5/5). Найдем одну часть:
1) 560 : 5 = 112 (м) – составляет одна часть Сашиного пути. А он прошел 2 таких части
2) 112 * 2 = 224 (м) – составляет 2/5 пути.
Ответ: 224 м.
А теперь ту же задачу превратим в нахождение числа по его дроби.
Саша прошел 224 м, что составляет 2/5 всего пути от дома до школы. Найди расстояние от дома до школы?
224 м – это часть пути, значит весь путь будет больше. Эта информация нужна для самопроверки. Найдем сначала 1/5 пути
1) 224 : 2 = 112 (м) – составляет 1/5 пути
2) 112 * 5 = 560 (м) – составляет весь путь
Ответ: 560 м.
Проверим себя. При нахождении дроби от числа результат будет меньше этого числа, если у нас правильная дробь, и больше, если неправильная (то есть целое + еще какая-то часть).
При нахождении числа от дроби – все наоборот, результат будет больше этого числа, если у нас правильная дробь, и меньше, если неправильная.
