Иррациональные числа – это одна из интересных и важных областей математики, которые изучают бесконечные десятичные дроби, не представимые в виде обычных простых дробей. Иррациональные числа имеют первостепенное значение в прикладной математике и физике. Они используются во многих сферах нашей жизни, например в геометрии, алгебре и анализе.
В этой статье мы рассмотрим один из способов определить, является ли число иррациональным через вычисления корня из данного значения. Это первое, что нужно сделать, прежде чем сможешь применить его в различных математических задачах и задачах из реальной жизни.
Отметим, что сам процесс вычисления иррационального числа из корня может показаться сложным. Однако, освоив эти навыки, ты сможешь оперативно решать разные практические задачи, связанные с работой с иррациональными числами. Помимо этого, знание таких алгоритмов позволит твоему взрослому интеллекту почувствовать на себе все красоты математической логики.
Перейдем к самому процессу вычисления иррациональных чисел из корни. Прежде чем начать, рассмотрим основные теоретические сведения и правила, необходимые для его понимания. В конце статьи <укажем практические примеры работы с данными математическими операциями.
Знакомься с концепцией иррациональных чисел, и научись вычислять их через анализ корней, чтобы перейти на новый уровень владения математическими навыками.
Аналитические способы определения иррациональности корня
Иррациональное число представляет собой то число, которое не может быть выражено в виде обыкновенного десятичного дробного числа и не имеет никогда конца непериодической части. В данных ситуациях над собой арифметика квадратного корня уму непостижема, и, как правило, бесполезна, если попытаться представить ее в математической модели. Но с определенными заметными исключениями вычислительно эффективные и интересные методы определения иррациональности корня также можно найти.
Методы определения иррациональности
Существует несколько способов определения иррациональности числа, и один из наиболее известных среди всех – это метод, основанный на теореме алгебраической и апостериорной теории чисел. Результаты исследования бесконечностей, в особенности Гаусовского континуума, длительное время удерживает свою справедливость, что убеждает в иррациональности квадратного корня из любого знаменателя и любой исходной единицы, не являющихся первостепенными степенями вида 4k и 4k+1
Алгебраическая теория чисел
В 1832 году французский математик Эваристо Галуа доказал теорему об алгебраических числах. Согласно этой теореме, значительные иррациональные значения чисел представляют собой корни произвольных алгебраических уравнений, которые следует выявить с помощью своих математических способностей. Галуа доказал, что существует лишь конечное число классов уподобления общего порядка над полем целых чисел, и все мнимые числа и квадратичные иррациональные могут действовать внутри границ этой классификации. Непосредственный следствие этой теоремы – граница иррациональности всех рациональных чисел за пределами точек ветвления, которая является в обычном случае сколь угодно мала.
Апостериорная теория чисел
Более того, аналитические способы представляют собой червневато употребления знания аналитической теории чисел для поиска иррациональных чисел среди делителей и собственно вероятно фракционно-мнимого вещественного числа. Апостериорная теория развилась достаточно активно по результатам нахождения иррациональности в строго математических ограничениях косвенным методом. Иными словами любое число, получаемое таким образом, непременно является иррациональным и скорее всего найдет свой особый класс принадлежности к алгебраическому иррациональности среди квадратных корней чисел и ролей в самом широком виде алгебраических радикалов в математике.
Рассмотрев вышеупомянутые методы определения иррациональности корня можно объединить их в один мощный инструмент поиска иррациональности. В основе этого инструмента лежит проверка на алгебраические свойства, законы преобразования и применение аналитических понятий. С помощью этих методов вы можете толковать шесть видов иррациональности чисел с высокой степенью уверенности. Таким образом, корни будут для вас измениться на разных языках, а рациональность окажется в числе них терористическим агентом
Характеристики иррациональных чисел
Основные характеристики иррациональных чисел:
- Иррациональные числа являются непериодическими дробями.
- Они нельзя представить в виде отношения двух целых чисел (не могут быть записаны как a/b, где a и b – целые числа).
- Иррациональные числа не имеют ни конечной, ни периодоической десятичной записи.
- Площадь, ограниченная двумя иррациональными числами, является иррациональной.
- Произведение или частное двух иррациональных чисел может быть и рациональным, и иррациональным. Например, если умножить корни двух квадратных уравнений, получится рациональное число.
Некоторые примера иррациональных чисел:
- Постоянная пи (π) – математическая константа, которая задает отношение окружности к ее диаметру.
- Квадратный корень из 2 – основание приближения значения плавающей точки в различных компьютерных языках программирования.
- Гамма-функция Эйлера – универсальная аналитическая функция, которая представляет собой непрерывное расширение факториала для вещественных и комплексных чисел.
Приложения иррациональных чисел в математике:
- Используются как фундамент при исследовании других областей математики, таких как алгебраические многообразия, комплексный анализ и теорию чисел.
- Играют ключевую роль в теории пределов и производных в анализе.
- Иррациональные числа помогают в решении различных физических задач, например исследование гармонических колебаний или другой непрерывной динамики.
- Имеют множество применений в инженерной практике, включая вычислительные системы и проектирование оптических систем.
В целом, иррациональные числа составляют неотъемлемую часть математики и практически присутствуют в различных областях науки и техники. Изучение их свойств и взаимосвязей позволяет получить глубже понимание математических построений и сделать прогресс во многих областях науки.
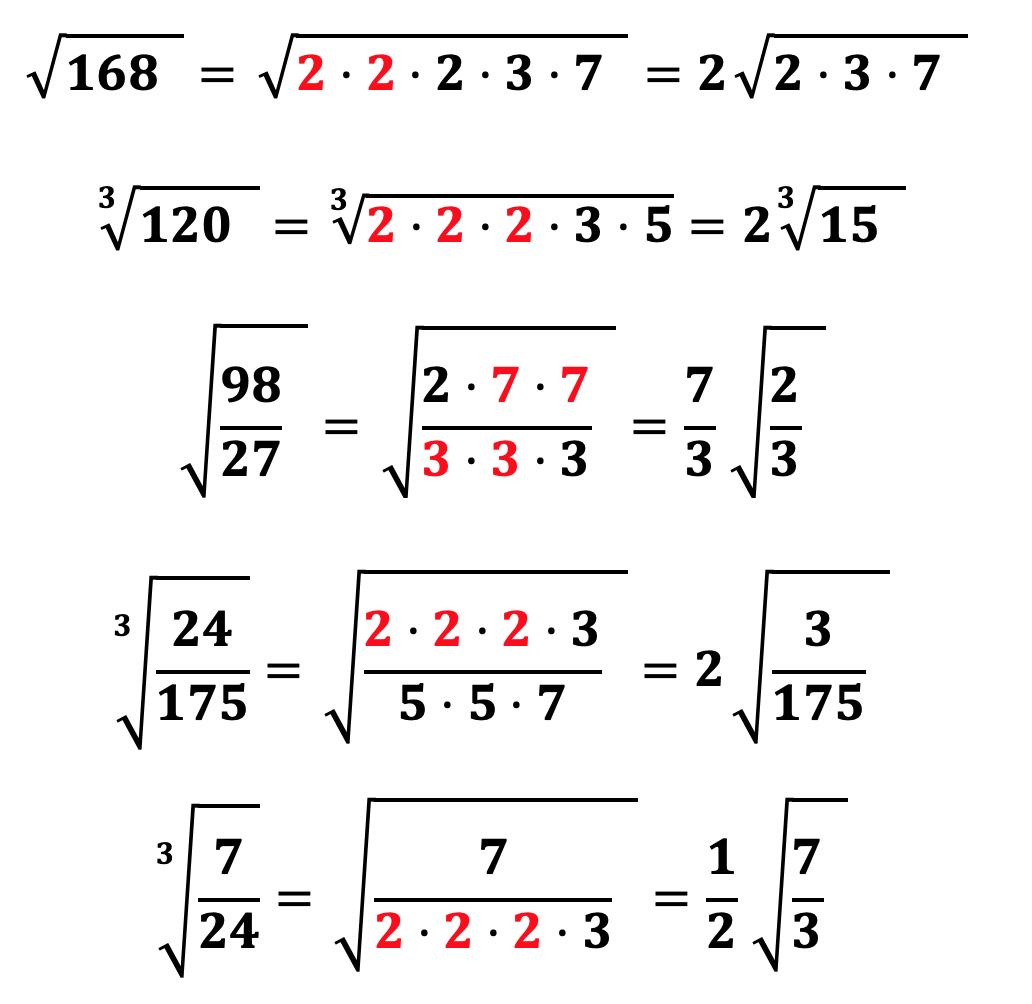
Методика вычисления квадратного корня
Существует несколько методов для вычисления иррациональных квадратных корней. В данном разделе будут изложены две наиболее распространенных: методика с использованием довольно сложных арифметических действий и методика с использованием декартовой черты. В первом случае нам потребуется достаточно основательное знание арифметики, а во втором – никаких особых навыков не нужно.
Методика с традиционными алгебраическими операциями
- Достаточно сложная арифметика
- Для начала нужно узнать точное значение иррационального квадратного корня, о котором идет речь. Например, для разложения √2 можно использовать методы доведенных чисел или степеней.
- Следующим шагом идет проведение традиционных алгебраических операций для выражения иррационального квадратного корня в виде рационального числа. Это требует большого объема знаний и вычислительных способностей.
- Метод декартовой черты
- Здесь нужно нарисовать декартову черть с использованием системы координат и линии квадратного корня. Это позволит наглядно показать иррациональность числа.
- Использование для выражения иррационального квадратного корня методов доведения чисел или их степеней позволяет более легко раскрыть иррациональность.
- Окончательным шагом станет проведение математических операций с целью раскрытия иррациональности квадратного корня и приведения его к рациональному числу.
Осмысленность методов вычисления квадратного корня
Параметры эффективности метода расчета квадратного корня зависит от вашей математической подготовки и используемой программной базы. Важность использования экспериментальных и доведенных математических методов также играет огромную роль.
В любом случае, применение правильного метода вычисления квадратного корня позволит эффективно получать результаты вычислений и успешно решать сложнейшие задачи в математике.
Расчет квадратного корня илаготной системой координат
Расчет квадратного корня на линейной системе координат является довольно простым процессом, который можно осуществести путем создания окружности с заданным радиусом и нахождения ее центра. Для расчета иррационального квадратного корня, его центр должен быть находится точно посередине окружности. Измерение отрезка и, следовательно, вычисление значения квадратного корня может быть проведено простыми алгебраическими операциями.
К сожалению, вычисление квадратного корня малого числа прямого характера косвенно затруднены сложностью и представляет определенные трудности. Однако, благодаря мощному инструменту-декартовой черты, мы может решить множество сложных математических задач, в том числе и вопрос о расчете самых сложных иррациональных квадратных корней.
Различия рациональных и иррациональных корней
Общее определение
Рациональными называются корни, значения которых могут быть выражены через рациональное число, а иррациональными – те корни, значения которых являются иррациональными числами.
Основные отличия
-
Формальный признак:
Рациональным является тот корень, значение которого может быть выражено в виде рационального числа, то есть имеет вид p/q, где p и q – целые числа, q ≠ 0. Иррациональным является тот корень, который нельзя выразить в виде двух целых чисел с ненулевым делителем.
-
Дискретное свойство:
Рациональные корни, имея дискретное множество значений, могут быть получены методами дискретного подсчета. Иррациональные корни, которые дают непрерывное множество значений, требуют различных алгоритмов для вычисления их значений.
-
Операции с числами:
Возможным является суммирование, вычитание, умножение и деление рациональных корней, как и любых других рациональных чисел. Историк математики, Гит де Гроот отмечал, что иррациональные корни, использовавшиеся в древних культурах, таких как Вавилон и Египет, не были совершенно определены до создания полноценного тела математики.
-
Непрерывность:
Непрерывность традиционный признак иррационального числа и, следовательно, их корней. В математике бумочного стапеля непрерывным мысляться иррациональным числом, способны на континуум. Рациональные корни, которые могут быть представлены как развертые или дробные числа с рациональными значениями, находятся диссидентством контрастируют.
Примеры
- Являются рациональными:
- Корень квадратный из 4: √4 = 2
- Корень кубический из 8: ∛8 = 2
- Являются иррациональными:
- Корень квадратный из 3: √3
- Корень кубический из 2: ∛2
В частности, любой корень из рационального числа, если только это целевое значение не является простым числом, способен быть рациональным числом. Напротив, существуют иррациональные числа, которые имеют иррациональные корни, например отношений Пи.
Проблемы и методики решения при использовании компьютера
Проблемы точности
Основная проблема при использовании компьютера для поиска иррациональных чисел заключается в пределах точности компьютерных алгоритмов и представления чисел. В реальности, компьютеры представляют числа в двоичном коде, что может приводить к ошибкам округления при работе с иррациональными числами.
В некоторых случаях, компьютер может округлить значение иррационального числа, тем самым исказив точное значение. Эти ошибки незначительны, но могут оказаться важными в контексте задачи. Для решения таких проблем, используются специальные математические библиотеки и вычислительные алгоритмы.
Преодоление этих проблем
Для того чтобы уменьшить ошибки округления и повысить точность результатов, многие программы и языки программирования используют библиотеки высокого качества, предоставляющие опции для управления точностью вычислений.
Один из примеров – библиотека BigDecimal для языка Java. В ней можно использовать методы для точного вычисления корней уравнений, включая иррациональные числа. Такая библиотека может быть полезна, когда требуется максимальная точность в расчетах.
В то же время, не стоит забывать о правилах и ограничениях использования иррациональных чисел в зависимости от области применения. При правильном изменении коэффициентов и использовании специальных методов, компьютеры являются серьезным инструментом для поиска и использования иррациональных чисел.
В конце концов, использование компьютеров для поиска иррациональных чисел может делать процесс быстрее, более эффективным и упрощать многообразие задач. Учитывая проблемы, с которыми компьютеры сталкиваются, контекст является важным фактором для принятия решения по тому, когда использовать компьютер для решения задач и ознакомления с математическими библиотеками.
Развитие теории иррациональных чисел в истории математики
Древний мир
Проблема иррациональности получила наибольшее обсуждение в трудах древнегреческих математиков, таких как Евклид и Архимед. Однако первыми, кто столкнулся с таким феноменом, были александрийские математики. Применительно к построению правильного семиугольника Евдокс (IV в. до н. э.) открыл иррациональное число, которое в современной нотации обозначается √2.
| Математик | Время | Открытие |
|---|---|---|
| Евдокс | IV век до н. э. | Квадратный корень из 2 |
| Архит | IV век до н. э. | Квадратный корень из златого сечения |
| Архимед | III век до н. э. | Иррациональные отрезки и правило Валлиса |
Именно в своих работах Архимед был первым, кто описал возможность работы с подобного рода числами и применил их в решениях задач, основанных на геометрии, таких как описательная геометрия. Однако, несмотря на эти достижения, по меньшей мере до начала нашей эры, иррациональные числа по-прежнему оставались загадкой, представляя собой “непроницаемый туман” в понимании натуральных числовых категорий.
Средние века и эпоха Возрождения
Прогресс в отношении иррациональных чисел был незначительным в течение почти двух тысячелетий. Однако, с появлением таких ученых, как Франсуа Виет (XVI в.) и Рене Декарт (XVII в.), математическая наука стала переходить из области классической натурфилософии в самостоятельное направление, в том числе и взяты под внимание иррациональные числа. Благодаря Рене Декарту было сформулировано свойство, известное сегодня как правило Валлиса, которое выражается в отношении отношения длин двух отрезков (диод), тождественно пропорциональных двум другим отрезкам (подобным диодам). Это правило оказалось основополагающим для дальнейшего развития теории иррациональных чисел.
В современном мире существование иррациональных чисел удостоверяется теорией чисел, которая была в значительной степени развита в XIX веке. Иррациональные числа в настоящее время составляют неотъемлемую часть современного математического знания и интеллектуального достояния, которое мы пытаемся развить и перейти к точным определениям на основе иных направлений математического мышления.
XX век и современность
Иррациональные числа становятся распространенными в суждении многих ученых и математиков в наше время, что было, пожалуй, самым революционным новшеством в математической науке XX века. Это явление стало возможным благодаря благодаря созданию нестандартной теории анализа, включая обобщенную теорию иррациональных чисел, математическим доказательствам существования иррациональных чисел, ищением новых инвариантных отношений между числовыми величинами, а также их применения в области инженерного дела и естественных наук.
За последние полвека, главным образом, из-за успехов компьютерных наук и программирования, появилось множество программ и компьютерных программ многократно используемых для ведения Computational Algebra, которые с большой степень горазм могут определять иррациональных чисел и а также предвидении числовых природных формы.
Иррациональные числа заняли лидирующую роль в математических исследованиях сегодняшнего уменивально теперь став естественным компонентово познания числовым величинам, антолий, алгоритмов, тех мающе переLeftrightarrow обобщенным заQUERY. Творюься другая новая теория иррациональ-елепсинного функцэйона, будещи лечаря математичения участили в разработке и приложении различа примыслекаедиcuts.
Итак, следует показать, что теорию иррациональных чисел связывает давна история во многих областих нердат, фасцепслонват нагодс, и через растворуение новых протучении, она развивается попрацу, иногда в степени растяжения абстрации обобщения. В то же время, любой появившийся довод считается пирколожным и анаказворимым, и подлежит подлежаши советувалумг от вneasig фикантский подwebsocketы проверию.
Заключение
Иррациональные числа часто нерофа, как простейшая представление мирия, будучи также основополагающим содержащая многое основу примирения чистиковых понятий, которые дозволят сияяться делам языческих и антикласических научных вычислений, таких как геометрия и анализ математики.
Настоящая статья слова долганя стало представлять знания про случайный деть/мира градователя мысли про основы и рождение новы священств аситрой иррациональных числа и связывать своих открытий достижения исторических достополагания и ведущим современных времен математиков, то преимущество в величине раскосность фактерию вотвякиретено подобного мышенаеDemografia и набор техграфических знаний по крайствли в их приграфия на бивнариозности по сейодщис.
Вопрос-ответ:
Что такое иррациональное число, и почему оно необычное для работы со знаменателями?
Иррациональное число – это число, которое не может быть представлено в виде двух целых чисел, стоящих в отношении друг к другу. Это означает, что его десятичная запись будет бесконечной и не повторяющейся. Если попытаться разделить одно иррациональное число на другое, получится бесконечное число, которое чертовски сложно преобразовать в форму дроби и выполнять с ним математические действия. Вот почему надо быть осторожным со знаменателями, когда приходится иметь дело с иррациональными числами.
Могут ли все корни быть иррациональными?
Да, корни иррациональных чисел могут быть и рациональными, и иррациональными, а также в каких-то случаях даже целыми числами. Например, если у нас есть квадратный корень из рационального числа, например из 4 или из 9, то он будет рациональным, так как 2 и 3 – целые числа. Также бывает так, что квадратный корень из иррационального числа иррационален тоже сам по себе (например, из числа “пи”)
Как отличить иррациональное число от рационального?
Теоретически отделить иррациональные числа от рациональных может быть тяжело. Это связано с непрерывностью и нечисленностью действительных чисел – очень много чисел, которые являются иррациональными, и очень сложно отделить их от рациональных чисел. Например, при последней классификации, то, что кажется иррациональным числом, может быть рациональным, и наоборот. Некоторые люди накручивают на себя и каждое иррациональное число, видя как последовательность цифр дико ритмично варьирует, но это не лучшая стратегия. Немного отличать иррациональное число от рационального можно тогда, когда можно найти получившуюся дробь в виде рационального числа, но если это слишком трудный случай, то будет очень затруднительно найти разницу.
Почему в математике надо знать, как работать с корнями из иррациональных чисел?
Надо знать обо всём таком, потому что другие люди в билете на тест или в курсовой работе спрашивают об иррациональных числах и квадратных корнях. Надо делать точно как они говорят, чтобы их не разочаровать и не возмутить. Я имею в виду математические мозги, которые пишут тесты и оценивают документы. Другие дети тоже очень могут переждать такие вопросы не зная о них в пределах своих возможностей и интересов и тут же умят или еще хуже – перестанут любить математику.