Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 августа 2021 года; проверки требуют 9 правок.
Коэффицие́нт упру́гости, иногда также коэффицие́нт Гу́ка, жёсткость пружи́ны, — коэффициент, связывающий в законе Гука удлинение упругого тела и возникающую вследствие этого удлинения силу упругости. Применяется в механике твердого тела в разделе упругости. Обозначается буквой k[1], иногда D[2] или c[3]. Имеет единицу измерения Н/м или кг/с2 (в СИ), дин/см или г/с2 (в СГС).
Коэффициент упругости численно равен силе, которую надо приложить к пружине, чтобы её длина изменилась на единицу расстояния.
Определение и свойства[править | править код]
Коэффициент упругости по определению равен силе упругости, делённой на изменение длины пружины:

Коэффициент упругости зависит как от свойств материала, так и от размеров упругого тела. Так, для упругого стержня можно выделить зависимость от размеров стержня (площади поперечного сечения 



Жёсткость деформируемых тел при их соединении[править | править код]
Параллельное соединение пружин.
Последовательное соединение пружин.
При соединении нескольких упруго деформируемых тел (далее для краткости — пружин) общая жёсткость системы будет меняться. При параллельном соединении жёсткость увеличивается, при последовательном — уменьшается.
Параллельное соединение[править | править код]
При параллельном соединении 


Последовательное соединение[править | править код]
При последовательном соединении 


Жёсткость некоторых деформируемых тел[править | править код]
Стержень постоянного сечения[править | править код]
Однородный стержень постоянного сечения, упруго деформируемый вдоль оси, имеет коэффициент жёсткости
где
- Е — модуль Юнга, зависящий только от материала, из которого выполнен стержень;
- S — площадь поперечного сечения;
- L0 — длина стержня.
Цилиндрическая витая пружина[править | править код]
Витая цилиндрическая пружина сжатия.
Витая цилиндрическая пружина сжатия или растяжения, намотанная из цилиндрической проволоки и упруго деформируемая вдоль оси, имеет коэффициент жёсткости
где
- dD — диаметр проволоки;
- dF — диаметр намотки (измеряемый от оси проволоки);
- n — число витков;
- G — модуль сдвига (для обычной стали G ≈ 80 ГПа, для пружинной стали G ≈ 78.5 ГПа, для меди ~ 45 ГПа).
См. также[править | править код]
- Закон Гука
- Сила упругости
- Роберт Гук
- Модуль Юнга
- Пружина
Источники и примечания[править | править код]
- ↑ Упругая деформация. Архивировано 30 июня 2012 года.
- ↑ Dieter Meschede, Christian Gerthsen. Physik. — Springer, 2004. — P. 181 ..
- ↑
Bruno Assmann. Technische Mechanik: Kinematik und Kinetik. — Oldenbourg, 2004. — P. 11 .. - ↑ Динамика, Сила упругости. Дата обращения: 22 мая 2012. Архивировано из оригинала 13 октября 2012 года.
- ↑ Механические свойства тел. Дата обращения: 22 мая 2012. Архивировано 15 февраля 2013 года.
Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины. Что же это за величина, и как она связана с деформацией тел и законом Гука?
Содержание:
- Сила упругости и закон Гука
- Определение коэффициента жесткости
- Расчет жесткости системы
- Последовательное соединение системы пружин
- Параллельное соединение системы пружин
- Вычисление коэффициента жесткости опытным методом
- Примеры задач на нахождение жесткости
- Видео
Сила упругости и закон Гука
Для начала определим основные термины, которые будут использоваться в данной статье. Известно, если воздействовать на тело извне, оно либо приобретет ускорение, либо деформируется. Деформация — это изменение размеров или формы тела под влиянием внешних сил. Если объект полностью восстанавливается после прекращения нагрузки, то такая деформация считается упругой; если же тело остается в измененном состоянии (например, согнутом, растянутом, сжатым и т. д. ), то деформация пластическая.
Примерами пластических деформаций являются:
- лепка из глины;
- погнутая алюминиевая ложка.
В свою очередь, упругими деформациями будут считаться:
- резинка (можно растянуть ее, после чего она вернется в исходное состояние);
- пружина (после сжатия снова распрямляется).
В результате упругой деформации тела (в частности, пружины) в нем возникает сила упругости, равная по модулю приложенной силе, но направленная в противоположную сторону. Сила упругости для пружины будет пропорциональна ее удлинению. Математически это можно записать таким образом:
F = – k·x;
где F — сила упругости, x — расстояние, на которое изменилась длина тела в результате растяжения, k — необходимый для нас коэффициент жесткости. Указанная выше формула также является частным случаем закона Гука для тонкого растяжимого стержня. В общей форме этот закон формулируется так: «Деформация, возникшая в упругом теле, будет пропорциональна силе, которая приложена к данному телу». Он справедлив только в тех случаях, когда речь идет о малых деформациях (растяжение или сжатие намного меньше длины исходного тела).
Определение коэффициента жесткости
Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:
k = F/x.
Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.
Единица измерения жесткости в СИ — Н/м.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.
Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
k = k1 + k2 + … + ki.
Измерение жесткости пружины опытным путем – в этом видео.
Вычисление коэффициента жесткости опытным методом
С помощью несложного опыта можно самостоятельно рассчитать, чему будет равен коэффициент Гука. Для проведения эксперимента понадобятся:
- линейка;
- пружина;
- груз с известной массой.
Последовательность действий для опыта такова:
- Необходимо закрепить пружину вертикально, подвесив ее к любой удобной опоре. Нижний край должен остаться свободным.
- При помощи линейки измеряется ее длина и записывается как величина x1.
- На свободный конец нужно подвесить груз с известной массой m.
- Длина пружины измеряется в нагруженном состоянии. Обозначается величиной x2.
- Подсчитывается абсолютное удлинение: x = x2-x1. Для того чтобы получить результат в международной системе единиц, лучше сразу перевести его из сантиметров или миллиметров в метры.
- Сила, которая вызвала деформацию, — это сила тяжести тела. Формула для ее расчета — F = mg, где m — это масса используемого в эксперименте груза (переводится в кг), а g — величина свободного ускорения, равная приблизительно 9,8.
- После проведенных расчетов остается найти только сам коэффициент жесткости, формула которого была указана выше: k = F/x.
Примеры задач на нахождение жесткости
Задача 1
На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.
- Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
- По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.
Ответ: жесткость пружины составит 2500 Н/м.
Задача 2
Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.
- Найдем силу тяжести, деформирующей пружину: F = mg = 10 · 9.8 = 98 Н.
- Определим коэффициент упругости: k = F/x = 98 / 0.04 = 2450 Н/м.
- Рассчитаем, с какой силой действует второй груз: F = mg = 25 · 9.8 = 245 Н.
- По закону Гука запишем формулу для абсолютного удлинения: x = F/k.
- Для второго случая подсчитаем длину растяжения: x = 245 / 2450 = 0,1 м.
Ответ: во втором случае пружина растянется на 10 см.
Видео
Из этого видео вы узнаете, как определить жесткость пружины.
Обычно при изучении закон Гука не вызывает особых сложностей. Запомнить, что деформация в упругом теле пропорциональна приложенной к нему силе, совсем не сложно.
Чаще всего, этого знания вполне достаточно для школьного курса, чтобы забыть про Гука навсегда :)… Чтобы он лучше запомнился, глянем на портрет.
Однако, если вы изучаете физику по углубленной программе или если ваш преподаватель хочет добиться демонстрации понимания этого закона на более высоком уровне, то сказанного явно недостаточно. Кроме того, при поступлении в технический институт, знаний этих тоже мало. Ведь на законе Гука держится великий и ужасный сопромат! Да и при изучении механики – это один из самых важных законов.
Давайте изложим основные постулаты Гука в простой и понятной читателю форме, ну а если вопросы останутся – пишем их в комментариях или в личку.
Введение и основные понятия
Наверняка вы в детстве играли с такой штукой, которая называется лук со стрелами. Принцип работы этого устройства очень прост. Есть согнутая палка, чаще всего из ивы, и есть тетива, которая связывает концы палки. Когда мы натягиваем тетиву стрелой, то сила упругости палки заставляет её возвращаться к прежнему состоянию и передавать энергию стреле.
Как вы догадываетесь, ключевое слово тут – сила упругости. Это такая сила, которая возникает в теле при попытке это тело согнуть или изменить его форму, то есть деформировать. Кстати, про силу полезно прочитать вот это. Обусловлена она внутренним взаимодействием частичек.
И тут тоже появилось новое слово – деформация. Думаю, пояснять что это такое, не нужно.
А вот сказать, что деформация бывает обратимая (упругая) и необратимая, важно. Ведь закон Гука работает в случаях существования упругой деформации.
Упругая деформация – это такая деформация, после которой тело возвращается к своим первоначальным геометрическим характеристикам, после снятия внешнего воздействия.
Простейшие виды деформации – это растяжение и сжатие. Сразу вспоминаем пружину. Ну и в учебнике физики вы как раз-таки встретите закон Гука, который раскрывается на примере пружины.
Формулировка закона Гука
Формулируется закон так:
Деформация, возникающая в упругом теле, пропорциональна приложенной к этому телу силе.
Если записывать его в виде формулы, то имеем следующее:
F = -kx ,
где F – сила упругости в теле, k – коэффициент упругости или жесткости, x – линейное изменение размеров тела.
Почему тут минус? Да его можно и не писать, если понимать логику. Вспоминаем, что сила есть вектор. Так как сила, возникающая в теле, противонаправлена силе приложенной, то формула записывается с минусом.
Иногда вместо k или x используют другие обозначения, но смысл от этого не меняется.
Разбираемся с новыми буквами
У нас появилась сила упругости в теле. Именно она в формуле – это F. Вспоминаем, что по третьему закону Ньютона (обязательно читаем), она равна силе или векторной сумме сил, воздействующей на тело. Мы считаем именно эту силу. Поэтому, если, скажем, предстоит решить задачу, где книга лежит на столе, а стол гнется, то мы считаем, что сила упругости в столе, равна нашему любимому m*g, так как книга притягивается к полу и вызывает изгиб стола.
k – это жесткость тела. Зависит она от материала и характеристик тела. Очевидно, что деревянная доска и железная труба будут иметь разные жесткости.
Стоит отметить, что это величина расчётная, но в начале изучения вы будете брать её из табличек и считать константой. А вот дальше нужно будет вспомнить/изучить, такую штуку, как модуль упругости первого рода или модуль Юнга. Это уже основы сопротивления материалов и начнется “О Боже, профессор нинада!”)
х – это линейное удлинение. Считается очень просто. Сколько стало минус сколько было :). В сложных случаях считается тоже посложнее, но нужны просто знания геометрии.
Новые важные понятия и обобщенный закон Гука
Про обобщенный закон Гука следует написать отдельную статью. Здесь же отмечу, что искушенный читатель наверняка заметил – пока речь идёт только об одноосном деформировании. Мы работаем с пружиной, которую можно растянуть вдоль оси икс или сжать вдоль оси икс. А что, если пружина будет растягиваться и сгибаться одновременно…
Реальные тела обычно деформируются во все стороны. В дело вступают сразу три направления.
В этом случае нужно использовать обобщенный закон Гука. Используются так называемые тензоры. Это большая тема, а тут отметим, что если вас вдруг спросили, а какие ограничения есть у стандартного закона Гука, то обязательно не забудьте сказать, что деформация должна происходить вдоль одной оси.
Ещё при разговоре об ограничениях выполнения закона стоит отметить про предел пропорциональности. Это максимальное механическое нагружение, до которого выполняется закон Гука. Смотрим на график. По оси Ыгрик у нас отложено механическое напряжение (читай как сила для упрощения), а по оси Ыкс – изменение размеров. Пока у нас есть линейная зависимость, отмеченная красной прямой линией, закон Гука будет выполняться.
Все тела ведут себя по разному и при достижении точки А одни тела развалятся/сломаются, а другие необратимо удлинятся/сожмутся. В конкретном примере тело расслюнявило, но оно не сломалось. Связь между силой и деформацией стала нелинейной.
Закон Гука выполняется только при малых деформациях и далеко не для всех материалов! Так, для многих полимеров закон Гука не будет выполняться. Выполняется он только, напомним, в линейных системах.
Как же описывать связь силы упругости и деформации в нелинейных системах, т.е. когда деформация не мала. Или что делать, когда закон Гука неприменим. Очень хорошо, что вы об этом задумались! Но это большая и сложная тема. Всё опять сводится к закону Гука в обобщенной форме и условно принимается, что деформация мала. Примерно так :)…
Но вообще, при больших деформациях следует использовать иные способа расчёта.
Как определить коэффициент жесткости
Коэффициент жесткости показывает, какую силу нужно приложить к телу, чтобы упруго деформировать его на единицу длины. Речь идет именно об упругой деформации, когда тело после воздействия на него снова принимает прежнюю форму. Для того чтобы найти эту величину, нужно деформировать тело, приложив к нему силу, или измерить потенциальную энергию его деформации.
Вам понадобится
- – калькулятор;
- – динамометр;
- – линейка.
Инструкция
Присоедините к телу динамометр и потяните за него, деформировав тело. Сила, которую покажет динамометр, будет по модулю равна силе упругости, действующей на тело. Найдите коэффициент жесткости, используя закон Гука, который говорит о том, что сила упругости прямо пропорциональна его удлинению и направлена в сторону, противоположную деформации. Рассчитайте коэффициент жесткости, поделив значение силы F на удлинение тела x, которое измерьте линейкой или рулеткой k=F/x. Чтобы найти удлинение деформированного тела вычтите длину деформированного тела от его первоначальной длины. Коэффициент жесткости измеряется в Н/м.
Если нет динамометра, подвесьте к деформируемому телу груз известной массы. Следите, чтобы тело деформировалось упруго и не разрушилось. В этом случае вес груза будет равен силе упругости, действующей на тело, коэффициент жесткости которого нужно найти, например, пружины. Рассчитайте коэффициент жесткости, поделив произведение массы m и ускорения свободного падения g≈9,81 м/с² на удлинение тела x, k=m•g/x. Удлинение измерьте по методике, предложенной в предыдущем пункте.
Пример. Под грузом 3 кг пружина длиной 20 см стала 26 см, определите ее жесткость. Сначала найдите удлинение пружины в метрах. Для этого от длины удлиненной пружины, вычтите ее длину в нормальном состоянии х=26-20=6 см=0,06 м. Вычислите жесткость, используя соответствующую формулу k=m•g/x=3•9,81/0,06≈500 Н/м.
В том случае, когда известна потенциальная энергия упруго деформированного тела, вычислите его жесткость. Для этого дополнительно измерьте его удлинение. Жесткость будет равна удвоенной потенциальной энергии Ер поделенной на квадрат удлинения тела х, k=2•Ep/x². Например, если мяч деформировался на 2 см и получил потенциальную энергию 4 Дж, то его жесткость k=2•4/0,02²=20000 Н/м.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Формула жесткости пружины в физике
Формула жесткости пружины
Определение и формула жесткости пружины
Определение
Силу, которая возникает в результате деформации тела и пытающаяся вернуть его в исходное состояние, называют силой упругости.
Чаще всего ее обозначают ${overline{F}}_{upr}$. Сила упругости появляется только при деформации тела и исчезает, если пропадает деформация. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.
Современник И. Ньютона Р. Гук установил зависимость силы упругости от величины деформации. Гук долго сомневался в справедливости своих выводов. В одной из своих книг он привел зашифрованную формулировку своего закона. Которая означала: «Ut tensio, sic vis» в переводе с латыни: каково растяжение, такова сила.
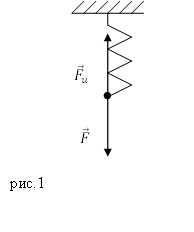
Рассмотрим пружину, на которую действует растягивающая сила ($overline{F}$), которая направлена вертикально вниз (рис.1).
Силу $overline{F }$ назовем деформирующей силой. От воздействия деформирующей силы длина пружины увеличивается. В результате в пружине появляется сила упругости (${overline{F}}_u$), уравновешивающая силу $overline{F }$. Если деформация является небольшой и упругой, то удлинение пружины ($Delta l$) прямо пропорционально деформирующей силе:
[overline{F}=kDelta lleft(1right),]
где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) $k$.
Жесткость (как свойство) – это характеристика упругих свойств тела, которое деформируют. Жесткость считают возможностью тела оказать противодействие внешней силе, способность сохранять свои геометрические параметры. Чем больше жесткость пружины, тем меньше она изменяет свою длину под воздействием заданной силы. Коэффициент жесткости – это основная характеристика жесткости (как свойства тела).
Коэффициент жесткости пружины зависит от материала, из которого сделана пружина и ее геометрических характеристик. Например, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси может быть вычислена как:
[k=frac{Gd^4}{8d^3_pn}left(2right),]
где $G$ – модуль сдвига (величина, зависящая от материала); $d$ – диаметр проволоки; $d_p$ – диаметр витка пружины; $n$ – количество витков пружины.
Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:
[left[kright]=left[frac{F_{upr }}{x}right]=frac{left[F_{upr }right]}{left[xright]}=frac{Н}{м}.]
Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.
Формула жесткости соединений пружин
Пусть $N$ пружин соединены последовательно. Тогда жесткость всего соединения равна:
[frac{1}{k}=frac{1}{k_1}+frac{1}{k_2}+dots =sumlimits^N_{ i=1}{frac{1}{k_i}left(3right),}]
где $k_i$ – жесткость $i-ой$ пружины.
При последовательном соединении пружин жесткость системы определяют как:
[k=k_1+k_2+dots +sumlimits^N_{i=1}{k_i}left(4right).]
Примеры задач с решением
Пример 1
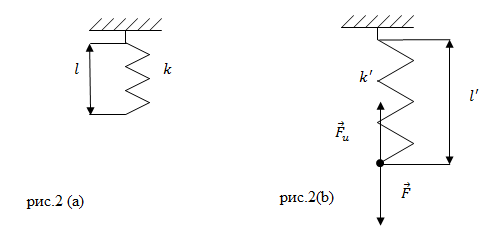
Задание. Пружина в отсутствии нагрузки имеет длину $l=0,01$ м и жесткость равную 10 $frac{Н}{м}. $Чему будет равна жесткость пружины и ее длина, если на пружину действовать силой $F$= 2 Н? Считайте деформацию пружины малой и упругой.
Решение. Жесткость пружины при упругих деформациях является постоянной величиной, значит, в нашей задаче:
[k=k’left(1.1right).]
При упругих деформациях выполняется закон Гука:
[F=kDelta l left(1.2right).]
Из (1.2) найдем удлинение пружины:
[Delta l=frac{F}{k}left(1.3right).]
Длина растянутой пружины равна:
[l’=l+Delta l=l+frac{F}{k}.]
Вычислим новую длину пружины:
[l’=0,01+frac{2}{10}=0,21 left(мright).]
Ответ. 1) $k’=10 frac{Н}{м}$; 2) $l’=0,21$ м
Пример 2
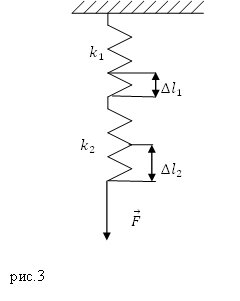
Задание. Две пружины, имеющие жесткости $k_1$ и $k_2$ соединили последовательно. Какой будет удлинение первой пружины (рис.3), если длина второй пружины увеличилась на величину $Delta l_2$?
Решение. Если пружины соединены последовательно, то деформирующая сила ($overline{F}$), действующая на каждую из пружин одинакова, то есть можно записать для первой пружины:
[F=k_1Delta l_1left(2.1right).]
Для второй пружины запишем:
[F=k_2Delta l_2left(2.2right).]
Если равны левые части выражений (2.1) и (2.2), то можно приравнять и правые части:
[k_1Delta l_1=k_2Delta l_2left(2.3right).]
Из равенства (2.3) получим удлинение первой пружины:
[Delta l_1=frac{k_2Delta l_2}{k_1}.]
Ответ. $Delta l_1=frac{k_2Delta l_2}{k_1}$
Читать дальше: формула закона Архимеда.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!