Графы – это разновидность упорядоченных пар вершин, которые служат мощным инструментом в исследованиях многих областей, от комбинаторики и теории графов до управления системами и связей между объектами в практических задачах.
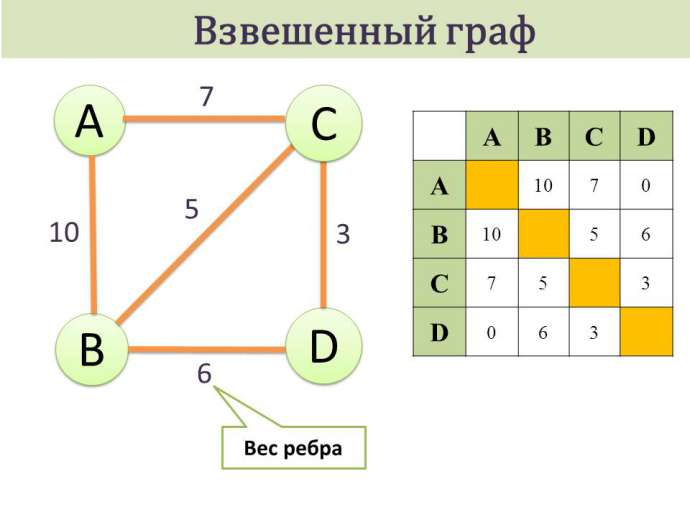
Определение графа: Граф – это математическая структура, состоящая из коллекции вершин (номеров узлов) и ребер (линий, соединяющих пары вершин). Вычисление количества ребер графа имеет важное значение для понимания комбинаторных и геометрических свойств графа.
В этой статье мы рассмотрим различные методы, которые позволят вам легко определить количество ребер в графе. Мы обсудим как теории, так и практические приложения, помогая анализировать и строить графы адекватно.
Нажмите “Продолжить чтение” для получения подробной информации о методах определения количества ребер графа и их применении.
Алгебраические методы вычисления ребер
Определение ребра: Ребро в графе определяется как соединение между двумя вершинами. Оно может быть направленным или без направления, и количество ребер в графе указывает на степень сложности и взаимосвязанности графа.
Алгебраический подход: Вычисление количества ребер в графе может быть осуществлено с использованием алгебраических методов, таких как рекуррентная формула, метода разложения графа на более простые подграфы, и решения систем уравнений.
Рекуррентная формула: Для простых графов используются рекуррентные формулы, которые позволяют находить количество ребер в зависимости от структуры графа. Например, для деревьев справедливо следующее уравнение: если имеется n вершин, то количество ребер равно n-1. Это происходит потому, что между любыми двумя вершинами есть ровно одно ребро, и для того, чтобы соединить все n вершин, нужно n-1 ребер.
Примечание: Рекуррентные формулы наиболее эффективны для простых графов без циклов, таких как деревья или цепочки. Для графов с более сложной структурой используются другие алгебраические методы.
Метод разложения графа: В случае, когда граф имеет более сложную структуру, можно разложить его на простые подграфы и посчитать количество ребер в каждом из них, а затем сложить эти значения. Этот алгоритм очень хорошо подходит для графов с большой вложенностью, таких как мультиграфы и гиперграфы.
Метод решения систем уравнений: Для графов с регулярной структурой можно составить систему линейных уравнений и решить их, чтобы найти количество ребер. Например, для регулярного графа заданной степени может быть составлена система, состоящая из уравнений вида a * d = 2 * e, где a – число вершин, d – степень регулярности графа, e – число ребер.
В заключении следует отметить, что алгебраические методы вычисления ребер являются мощным инструментом для анализа и оценки графов. Они особенно эффективны при работе с простыми и регулярными графами, а также в случае необходимости выполнения разложения графа на подграфы.
Математическая интерпретация графа
Определение графа
В математике граф определяется как пара G(V, E), где V – множество вершин, а E – множество рёбер. Ребро представляет собой пару вершин, соединённых между собой. Если ребро ориентировано, это означает, что он имеет направление, а если нет – речь идёт о неориентированном графе.
Свойства графа
- Степень вершины: Степень вершины обозначает количество рёбер, которые инцидентны данной вершине. В неориентированном графе степень относится к количеству соединений, а в ориентированном – к входящим и исходящим связям.
- Ширина графа: Ширина графа представляет собой минимальное число подграфов, которые могут быть получены путём разбиения графа на отдельные компоненты.
- Расстояние: Расстояние между двумя вершинами в графе – наименьшее число рёбер, которые нужно пройти для достижения одной вершины из другой.
Типы графов
- Нелинейный граф: Граф, в котором нет циклов, то есть любое ребро не инцидентно самому себе или другому ребру.
- Полный граф: Граф, в котором каждая пара вершин соединены ребром. В таком случае существует n(n-1)/2 рёбер для графа с n вершинами.
- Циклический граф: Граф, в котором все вершины образуют единственный или несколько циклов.
Приложения графов
Графы находят широкое применение в различных областях: от изучения социальных сетей и поиска путей в компьютерных сетях до моделирования химических молекул и искусственного интеллекта. Они дают возможность описать сложные системы и моделировать процессы в понятной и логичной форме.
Итог
Графы служат мощным математическим инструментом для описания соединений, связей и структурных свойств. Их использование в разных областях науки и техники позволяет понять и решить множество проблем и обнаружить закономерности, которые в противном случае были бы сложно интерпретировать.
Сравнение степеней вершин
В теории графов степенью вершины называем число рёбер, оканчивающихся на этой вершине. Речь идёт о мере важности вершины в графе, даже называемой её степени подключения или степени. Это позволяет по-разному характеризовать графы и найти интересные характеристики и законы. Например, параметры степеней вершин играют ключевую роль в показателе степенной ассоциации графа. Такое сравнение степеней вершин помогает провести сравнение их степендей в глобальном масштабе.
Число рёбер
Простой способ получить количество рёбер между вершинами находится через использование многогранника (или полногранника) с n вершинами. Многогранник или полногранник – это совокупность точек, рёбер и граней треугольной призмы (глаткая фигура). Вычисление числа рёбер между вершинами для полного графа на основе двух вершин, можно получить следующим образом:
k[n] = kn(k – 1)/2
Здесь k – степень вершины, n – число вершин в графе. То есть, для графа с n – вершинами, квадрат каждой вершины разбивается на n(n-1)/2 рёбер. Если мы по-строгому определим степень вершин как количество рёбер, которые исходят из вершины, то каждая вершина на самом деле имеет энлиту список рёбер не учеты вершин. Эти значения сильно влияют на структуру графа и его поведение.
Сравнение степеней вершин
Между степенями вершин в графе можно сравнивать их согласно их природе, выявляя свойства, такие как степенную ассоциацию и степенную диффуруцию. Например, степенная ассоциацию представлена отношением количества рёбер между вершинами и длины всех рёбер, так как степень вершины определяется суммой длин всех рёбер, которые исходят от вершины. Степенную диффуруцию можно рассматривать как отношение количества рёбер и отрезков между вершинами без учета их степеней:
Уравнение диффуромодуляции:
М[n] = SUM(D[i] ∗ dij)
Здесь M(n) – матрица рёбер графммы с n вершинами, n(i, j) – графмы рёбер между вершинами i и j, широта и сильная противность. Согласно уравнению, эту метрику можно найти путем сложения множителей синаптических датчиков диаметры из вершины к самим вершинам.
Таким образом, при изучении аспектов степеней вершин в графах, можно выявить решения, которые удовлетворяют принципу наименьшей работы и ставят новые подходы к изучению использования и взаимных связей треугольных призм.
Использование формулы Харари
Формула Харари: если у нас есть граф состоящий из n вершин (точек) и из m ребер (линий соединяющих вершины), то количество ребер m пропорционально н-му слагаемому степени 1/2, а именно можно найти его по этой формуле: m = (n*(n-1))/2.
Для четкого понимания как получается такое соотношение, рассмотрим это на примере двух вершин, где n=2. К графику можно добавить одно ребро, как показано ниже:
1 – 2
Отсюда теория:
1 узел will не удалить с его видимостью 1 ребером,
который уже связан с соответствующим рядом.
Выберите следующий из n узлов, который относится к 1-му узлу.
Для каждого из этих n-2 узлов, добавьте 1 ребро.
Таким образом, общая смета составит n-1 слагаемых 1.
Мы можем заключить так:
m ≤ (n∗(n-1))/2
Если граф насчитывает 10 вершин (точек) например, то м-макс = 10*(10-1)/2 = 45
Более просто это может быть обозначено графически:
1 – 2 – 3 – 4 – 5 – 6 – 7 – 8 – 9 – 10
Однако начальные местоположения n и m позволят узнать количество рёбер в графах, поскольку польза данного метода состоит в том, что если знать конечное количество рёбер в графе, то это число n должно быть таким, что n*(n-1) деленное на 2 равно этому количеству. В реальной жизни, как правило, у груза будут только частичные характеристики графа, такие как количество ребер и количество точек (вершин), поскольку во всей системе находитсяся множество исследуемых грузов.
Применение формулы Харари
Формула Харари широко распространена в исследованиях и проведении управленческих решений особенно в компаниях и областях, которые исходят из математического контекста и графических возможностей. Формула может быть применена к другим объектам, а не только к пару связанных вершин. Например, можно воспользоваться формулой для поиска связей между 2 компаниями или группами людей.
Применение формулы Харари позволяет вычислять количество связей и влияния между разными структурами и грузами внутри крупного графа. В определённых случаях, таких как исследования соседства в наблюдениях о социальных сетях, данная формула может быть необходимой для определения влияния каждого узла на соседей близлежащих узлов.
Ограничения формулы Харари
Ограничения формулы Харари обусловлены понятием что формула не применима для графов, которые состоят из валов и не имеют простого объединения. В графах с петлями или несколькими ребрами мы не можем определить степени связанности между разными узлами и мы должны освещать исключительные случаи обработки таких графов. Кроме того, возможности формулы Харари основаны на наборе исходных данных, если кластеры графа основаны на чётко заданных первоначальных элементах работы, то формула может быть принудительно применена, а если данные заполняются арбитрарно без определённых правил, то результаты формулы Харари вида получатся трудными для определения и поддающимися сомнению.
Хотя форма Харари была разработана для графов с определёнными атрибутами рёбер и вершин, существуют некоторые графы, которые могут дать непредвиденные результаты формулы Харари. Например, для валов или неоднородных графов значения степеней рёбер и вершин будут различными и непропорциональными и результат формулы Харари будет ложным.
Использование формулы Харари – это важная способность в структуре математических стратегий и способности анализировать выигрышные моменты в графе для улучшения решений и управления знаниями. Хотя ограничения применении формулы Харари напоминают о том, что все графы не имеют подходимий структуры и связей, в которых кажется выгодным применять эту формулу, манипуляции с формулой Харари остаются полезным методом в арсенале стратегических решений математиков и данных аналитиков.
Метод наивной перестановочной построения
Метод наивной перестановочной построения представляет собой машиностроительный способ определения количества ребер в графе. Этот метод может быть полезен для понимания базовой структуры графа или для анализа сети взаимосвязанных объектов, таких как сайты или социальные сети.
Принцип работы метода
Метод наивной перестановочной построения основывается на пошаговом подсчете связей между узлами графа с их удалением или перестановкой. В этом методе необходимо учесть все возможные пары узлов, чтобы избежать перечисления дублирующихся или неправильных ребер.
Отметим, этот метод влечет за собой значительное увеличение сложности вычислений с ростом количества узлов и ребер в графе.
Стратегия построения
Сначала создаем список всех пар узлов в графе, при этом, если граф ориентирован, анализируем его направление, иначе учитываем только существование связи.
Затем для каждой пары узлов исчёркиваем их ребро из списка уже подсчитанных ребер: если ребро уже не существует в списке, переходим к следующей паре.
При очередной итерации проверяем, есть ли новые пары узлов в списке, которые еще не были раскрыты, и вычисляем их количества ребер, уменьшая количество нового ребра на количество добавленных ранее.
Эту процедуру повторяем до тех пор, пока не получим конечное интегральное значение количества ребер в графе, которое является численной характеристикой его структуры.
Преимущество метода заключается в возможности точного определения количества ребер без привлечения дополнительных инструментов, однако не стоит забывать о потенциально высокой временной затрате при анализе больших графов.
Теория Рамсея и ее применение к графам
Теория Рамсея стремится найти минимальное количество элементов в структуре данных, при котором гарантированно появляются определенные структуры внутри нее. Например, для графов теория Рамсея помогает ответить на вопрос, в каком максимальном количестве вершин можно нарисовать граф, в котором нет красного клики размера р и синего клики размера q. В таком случае говорим о числах Рамсея R(r, q).
Алгоритмы для вычисления чисел Рамсея и анализ их поведения являются сложной проблемой, многие случаи которой остаются нерешенными. Однако теоретические результаты, полученные благодаря теории Рамсея, оказались очень полезными и применяются в разных областях математики, комбинаторике, теории информации и вычислительной сложности.
В частности, в области теории графов теоретические числа Рамсея позволяют строить графы с определенными свойствами, например, убедиться, что искомый граф не содержит требуемых подграфов (таких как циклы или клики), позволяя таким образом уменьшить поиск подходящих решений и повысить эффективность алгоритмов.
Применение теории Рамсея к задачам комбинаторных оптимизаций:
Теория Рамсея оказывает существенное влияние на задачи комбинаторной оптимизации, такие как раскрашивание графов, задача о поездках коммивояжера и графовые кодирования. Например, достаточное количество цветов для раскраски графа без треугольников может быть выведено из числа Рамсея для соответствующей пары. Теория Рамсея также может быть использована для построения графов с известными ограничениями на определённые типы структур внутри графа.
В целом, теория Рамсея представляет собой мощный инструмент для исследования графов и факторизацию матриц, способствуя успешному решению задач в теории графов, комбинаторике и вычислительной сложности.
Вопрос-ответ:
Сколько ребер может иметь граф?
Количество ребер у графа зависит от его количества вершин и степени связанности. Для простого графа без петель и кратных рёбер каждая вершина может быть связана с любыми другими, и количество ребер ограничено числом возможных пар вершин. В общем случае для графа с n вершинами количество ребер может варьироваться от 0 до n * (n – 1) / 2.
Можно ли найти количество рёбер графа, если неизвестны все вершины и связи между ними?
Для того чтобы найти точное количество ребер в графе, необходимо иметь полную информацию об узлах и их связи друг с другом. Если все вершины и связи между ними неизвестны, то угадать количество ребер практически невозможно, так как множество вариантов может быть очень большим. Однако, если имеется хоть какая-то информация о графа или его свойства, то конечно можно сделать предположения о количество ребер и о степени связности в целом.