Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Запомните!
Квадратичная функция — это функция вида
y = ax2 + bx + c,
где a,
b и с — заданные числа.
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».
| Квадратичная функция | Коэффициенты |
|---|---|
| y = 2x2 − 7x + 9 |
|
| y = 3x2 − 1 |
|
| y = −3x2 + 2x |
|
Как построить график квадратичной функции
Запомните!
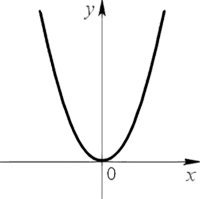
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
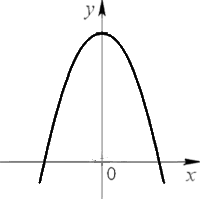
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции «y = x2 −7x + 10».
- Направление ветвей параболы
Запомните!
Если «a > 0», то ветви направлены вверх.
Если «a < 0», то ветви направлены вниз.
В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
- Координаты вершины параболы
Запомните!
Чтобы найти «x0»
(координата вершины по оси «Ox»)
нужно использовать формулу:Найдем «x0» для нашей функции «y = x2 −7x + 10».
Теперь нам нужно найти «y0»
(координату вершины по оси «Oy»).
Для этого нужно подставить найденное значение «x0» в исходную функцию.
Вспомнить, как найти значение функции можно в уроке
«Как решать задачи на функцию» в подразделе
«Как получить значение функции».y0(3,5) =
(3,5)2 − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =−12,25 + 10 = −2,25
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат.
Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
относительно оси «Oy». - Нули функции
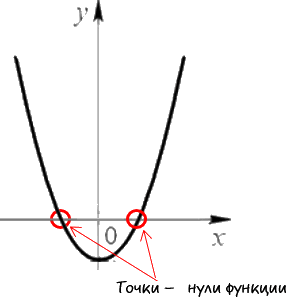
Для начала давайте разберемся, что называют нулями функции.
Запомните!
Нули функции — это точки пересечения графика функции с осью «Ox»
(осью абсцисс).Наглядно нули функции на графике выглядят так:
Свое название нули функции получили из-за того, что у этих точек координата
по оси «Oy» равна нулю.Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Запомните!
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
«y = 0».Подставим в заданную функцию «y = x2 −7x + 10»
вместо «y = 0» и решим полученное
квадратное уравнение
относительно
«x» .0 = x2 −7x + 10
x2 −7x + 10 = 0x1;2 =
7 ±
√49 − 4 · 1 · 102 · 1 x1;2 =
x1;2 =
x1 = x2 =
x1 = x2 =
x1 = 5 x2 = 2
Мы получили два корня в уравнении, значит, у нас две точки пересечения
с осью «Ox».
Назовем эти точки и выпишем их координаты.- (·) B (5; 0)
- (·) C (2; 0)
Отметим полученные точки («нули функции») на системе координат.
- Дополнительные точки для построения графика
Возьмем четыре произвольные числовые значения для «x».
Целесообразно брать целые числовые значения на оси «Ox»,
которые наиболее близки к оси
симметрии. Числа запишем в таблицу в порядке возрастания.x 1 3 4 6 y Для каждого выбранного значения «x»
рассчитаем «y».- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
4 -
y(3) = 32 − 7 · 3 + 10 = 9 − 21 + 10 =
−2 -
y(4) = 42 − 7 · 4 + 10 = 16 − 28 + 10 =
−2 -
y(6) = 62 − 7 · 6 + 10 = 36 − 42 + 10 =
4
Запишем полученные результаты в таблицу.
x 1 3 4 6 y 4 −2 −2 4 Отметим полученные точки графика на системе координат (зеленые точки).
Теперь мы готовы построить график.
На забудьте после построения подписать график функции. - y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.
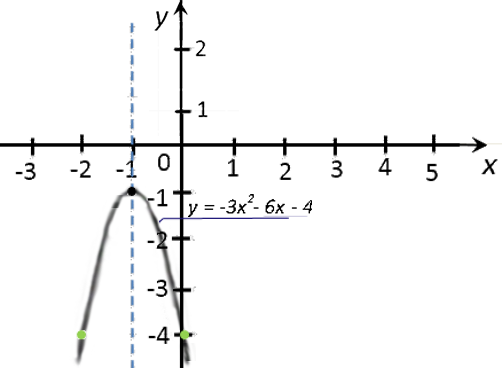
Пусть требуется построить график функции
«y = −3x2 − 6x − 4».
- Направление ветвей параболы
- Координаты вершины параболы
x0 =
x0 = == −1
y0(−1) = (−3) · (−1)2 − 6 · (−1) − 4 =
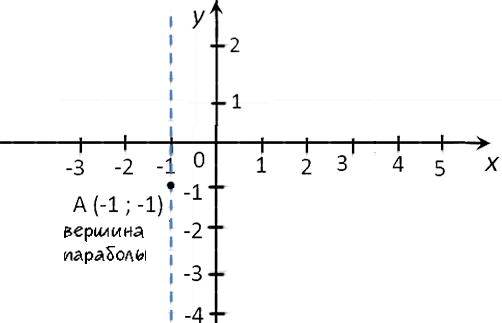
−3 · 1 + 6 − 4 = −1(·) A (−1; −1)
— вершина параболы.
- Нули функции
Точки пересечения с осью «Ox» (y = 0).
0 = −3x2 − 6x − 4
−3x2 − 6x − 4 = 0 |·(−1)
3x2 + 6x + 4 = 0
x1;2 =
−6 ±
√62 − 4 · 3 · 42 · 1 x1;2 =
x1;2 =
Ответ: нет действительных корней.Так как корней нет, значит, график функции не пересекает ось
«Ox». - Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x2 − 6x − 4».- y(−3) = −3 · (−3)2 − 6 · (−3) − 4
= −3 · 9 + 18 − 4 = −27 + 14 = −13 -
y(−2) = −3 · (−2)2 − 6 · (−2) − 4
= −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4 -
y(0) = −3 · 02 − 6 · 0 − 4
= −4 -
y(1) = −3 · 12 − 6 · 1 − 4
= −3 −6 − 4 = −13
x −3 −2 0 1 y −13 −4 −4 −13 - y(−3) = −3 · (−3)2 − 6 · (−3) − 4
«a = −3» — ветви параболы направлены вниз.
Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.
Функция вида 

В уравнении квадратичной функции:
a – старший коэффициент
b – второй коэффициент
с – свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции 
Обратите внимание на точки, обозначенные зелеными кружками – это, так называемые “базовые точки”. Чтобы найти координаты этих точек для функции 
Внимание! Если в уравнении квадратичной функции старший коэффициент 

График функции 
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции 

Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции 

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции 

В случае квадратичной функции 

Теперь внимание!
В процессе решения квадратного уравнения мы находим дискриминант: 
И здесь возможны три случая:
1. Если 



2. Если 



3. Если 



Если 
Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
Следующий важный параметр графика квадратичной функции – координаты вершины параболы:
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции – точка пересечения параболы 
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы 

То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой 
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции
1. Направление ветвей параболы.
Так как 
2. Найдем дискриминант квадратного трехчлена

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение:

3. Координаты вершины параболы:
4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:
Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции
Кррдинаты вершины параболы
Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:
Нанесем эти точки на координатную плоскость и соединим плавной линией:
2. Уравнение квадратичной функции имеет вид 

или в уравнении квадратичной функции 

Построим для примера график функции 
Вспомним линейные преобразования графиков функций. Чтобы построить график функции 
- сначала построить график функции
,
- затем одинаты всех точек графика умножить на 2,
- затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- а затем вдоль оси OY на 4 единицы вверх:
Теперь рассмотрим построение графика функции 

Выделим в уравнении функции полный квадрат:
Следовательно, координаты вершины параболы: 
3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции – точки пересечения графика функции с осью ОХ:
(х-2)(х+1)=0, отсюда
2. Координаты вершины параболы:
3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:
График квадратичной функции.
Перед вами график квадратичной функции вида .
Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
– ширины графика функции от значения коэффициента
,
– сдвига графика функции вдоль оси
от значения
,
– сдвига графика функции вдоль оси
от значения
– направления ветвей параболы от знака коэффициента
– координат вершины параболы от значений
и
:
Скачать таблицу квадратичная функция
И.В. Фельдман, репетитор по математике.
Эта статья — о числовой функции одной переменной. О функции второй степени с несколькими переменными см. Квадратичная форма; о геометрическом месте точек см. Парабола.
График функции
Квадратичная функция — целая рациональная функция второй степени вида 


Обзор основных свойств[править | править код]
Многие свойства квадратичной функции 

| Свойство | 
|

|
|---|---|---|
| Область определения функции | 
|
|
| Множество значений функции | 
|
![{displaystyle E(f)=left(-infty ;-{frac {b^{2}-4ac}{4a}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80574007c87fd2e0a084cba4db58f5eaa2f68950)
|
| Чётность функции | Чётная функция при  ; ни чётная, ни нечётная при ; ни чётная, ни нечётная при 
|
|
| Периодичность функции | Непериодическая функция | |
| Непрерывность функции | Всюду непрерывная функция, точек разрыва нет | |
| Нули функции |  , если , если  нет действительных нулей, если 
|
|
Предел функции при 
|
 при при 
|
 при при 
|
| Дифференцируемость функции | Всюду многократно дифференцируема:
|
|
| Точки экстремума (абсолютный экстремум) |  (минимум) (минимум)
|
 (максимум) (максимум)
|
| Интервалы строгой монотонности | убывает на ![{displaystyle left(-infty ;-{frac {b}{2a}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae6b6c026c5999b70af07f10b99f04c9f3eb4cc4) возрастает на 
|
возрастает на ![{displaystyle left(-infty ;-{frac {b}{2a}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae6b6c026c5999b70af07f10b99f04c9f3eb4cc4) убывает на 
|
| Выпуклость функции | Всюду выпуклая вниз функция | Всюду выпуклая вверх функция |
| Точки перегиба | Точки перегиба отсутствуют | |
| Ограниченность функции | Ограничена снизу | Ограничена сверху |
| Наибольшее значение функции | Отсутствует (неограничена сверху) | 
|
| Наименьшее значение функции | 
|
Отсутствует (неограничена снизу) |
| Положительные значения функции | 
|

|
| Отрицательные значения функции | 
|

|
Влияние коэффициентов на трансформацию графика[править | править код]
Стандартная запись уравнения квадратичной функции[править | править код]
Влияние коэффициентов 


Действительные числа 




По значению коэффициента 
- Если
, то ветви параболы направлены вверх, то есть её вершина расположена снизу.
- Если
, то ветви параболы направлены вниз, то есть её вершина расположена сверху.
- Если
, то парабола сжата по оси ординат, то есть кажется более широкой и плоской.
- Если
, то парабола растянута по оси ординат, то есть кажется более узкой и крутой.
Влияние значения коэффициента 




Изменение коэффициента 








Коэффициент 



Запись квадратичной функции через координаты вершины параболы[править | править код]
Любая квадратичная функция 













Влияние коэффициентов в записи вида 
Преобразовать произвольную квадратичную функцию вида 

-
, где
и
-
Сравнивая значения для 

Недостатком данного метода является его громоздкость, особенно в случае, когда в результате вынесения за скобки приходится работать с дробями. Также он требует определённого навыка в обращении с формулами сокращённого умножения.
Однако, рассмотренное выше доказательство в общем виде приводит к более простому способу вычисления координат вершины параболы с помощью формул 


.
Таким образом, 
Нули функции[править | править код]
Число нулей квадратичной функции[править | править код]
Число действительных нулей квадратичной функции в случае
Квадратичная функция является целой рациональной функцией второй степени, поэтому она может иметь не более двух нулей в действительной области. В случае расширения на комплексную область можно говорить о том, что квадратичная функция в любом случае имеет ровно два комплексных нуля, которые могут быть строго действительными числами или содержать мнимую единицу.
Определить число нулей квадратичной функции без решения соответствующего квадратного уравнения можно с помощью вычисления дискриминанта. При этом имеются различные вариации его вычисления: обычный (применим всегда), сокращённый (удобен в случае чётного коэффициента 
| Полный дискриминант | Сокращённый дискриминант | Приведённый дискриминант |
|---|---|---|
 |
 |

|
 |
 |

|
Независимо от вычисления дискриминанта будут справедливы следующие утверждения:
Например, для функции 
.
Это означает, что данная функция имеет два действительных нуля, то есть её парабола пересекает ось абсцисс в двух точках.
Методы вычисления нулей квадратичной функции[править | править код]
Нахождение нулей квадратичной функции сводится к решению квадратного уравнения 

- В наиболее общем случае применяется универсальная формула:
-
- Получить приведённую форму из общей можно, поделив исходное уравнение
на
. При этом, очевидно,
и
.
Чётность и симметрия квадратичной функции[править | править код]
Симметрия относительно оси ординат[править | править код]
График функции 


Квадратичная функция 

Кроме того, очевидно, что квадратичная функция является чётной только при отсутствии показателя 1, что означает 

, то есть
.
Таким образом, квадратичная функция является симметричной относительно оси ординат только тогда, когда 



Во всех других случаях квадратичная функция не будет ни чётной, ни нечётной, то есть является функцией общего вида. Это также легко можно показать с помощью определения чётности функции:
, то есть
.
, то есть
.
Осевая симметрия в общем случае[править | править код]
Осью симметрии любой параболы является прямая, проходящая через её вершину параллельно оси ординат
В то же время график любой квадратичной функции обладает осевой симметрией. Как известно, если для некоторой функции 







Доказательство этого факта также не является сложным:
К аналогичному результату приводит и преобразование:
Таким образом, 

Вычисление вершины параболы с помощью нулей функции[править | править код]
Нули функции расположены симметрично к оси, проходящей через вершину параболы параллельно оси ординат
Так как ось симметрии параболы всегда проходит через её вершину, то, очевидно, что нули квадратичной функции также всегда симметричны относительно абсциссы вершины параболы. Этот факт позволяет легко вычислить координаты вершины параболы с помощью известных нулей функции. В поле действительных чисел этот способ действует только тогда, когда парабола пересекает ось абсцисс или касается её, то есть имеет нули из действительной области.
В случае, когда квадратичная функция имеет лишь один нуль (кратности 2), то он, очевидно, сам и является вершиной параболы. Если же парабола имеет нули 


Особенно удобным этот способ будет в случае, когда квадратичная функция заданна в её факторизированном виде. Так, например, парабола функции 
При этом даже не требуется преобразовывать уравнение функции к общему виду.
Исследование методами дифференциального и интегрального анализа[править | править код]
Производная и первообразная[править | править код]
Квадратичная функция (красный график), её производная (синий) и первообразная (чёрный)
Угловой коэффициент касательной параболы в точке 

Как и любая целая рациональная функция квадратичная функция 





Квадратичная функция как и любая целая рациональная функция также и интегрируема во всей своей области определения. Её первообразная, очевидно, является кубической функцией:
, где
.
Монотонность и точки экстремума[править | править код]
Очевидно, что вершина параболы является её наивысшей или наинизшей точкой, то есть абсолютным экстремумом квадратичной функции (минимумом при 


Согласно необходимому и достаточному условию для существования экстремума, получаем: 








Вершина параболы разбивает область определения квадратичной функции на два монотонных интервала: 



При этом можно вовсе не запоминать данные формулы, а просто каждый раз пользоваться критериями существования экстремума для каждой конкретной квадратичной функции. Или же рекомендуется запоминать только формулу 
Например, для функции 
.
Таким образом, вершина параболы данной функции имеет координаты 


Выпуклость и точки перегиба[править | править код]
Так как вторая производная квадратичной функции 



Обратимость квадратичной функции[править | править код]
Функция 

Так как квадратичная функция не является строго монотонной функцией, то она является необратимой. Так как любую непрерывную функцию, однако, можно обратить на её интервалах строгой монотонности, то для любой квадратичной функции существуют две обратные функции, соответствующие двум её интервалам монотонности. Обратными для квадратичной функции на каждом из её интервалов монотонности являются функции арифметического квадратного корня[2].
Так, функция арифметического квадратного корня 




![{displaystyle (-infty ;0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72c148ad1ad5af487ca5ae78ee670d0d3605a243)



Функция 

Для нахождения обратных функций для произвольной квадратичной функции 






Таким образом, обратной к 


На интервале ![{displaystyle (-infty ;x_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b851e43347b4ceced99ed4c5b14a71e746675021)


Например, для функции 

на интервале
.
на интервале
.
Примеры появления на практике[править | править код]
- Зависимость высоты свободно падающего тела от времени.
- Зависимость площади круга от её линейных размеров (например, радиуса).
- Зависимость расстояния от времени при равноускоренном движении.
- Зависимость напора от расхода (напорная характеристика центробежного насоса).
Обобщение[править | править код]
Обобщение на случай многих переменных служат поверхности второго порядка, в общем виде такое уравнение можно записать, как:
.
Здесь: 


Свойства функции, так же как и в одномерном случае, определяются главным коэффициентом — матрицей 
См. также[править | править код]
- Аффинно-квадратичная функция
Примечания[править | править код]
- ↑ Квадратичная функция // Большая школьная энциклопедия. — М. : «Русское энциклопедическое товарищество», 2004. — С. 118—119.
- ↑ Rolf Baumann. Quadratwutzelfunktion // Algebra: Potenzfunktionen, Exponential- und Logarithmusgleichungen, Stochastik : [нем.]. — München : Mentor, 1999. — Т. 9. — С. 17—19. — 167 с. — ISBN 3-580-63631-6.
Литература[править | править код]
- Сканави М.И. График квадратного трёхчлена // Элементарная математика. — 2-е изд., перераб. и доп. — М., 1974. — С. 130—133. — 592 с.
- Каплан И.А. Тридцать третье практическое занятие (экстремум квадратичной функции) // Практические занятия по высшей математике. — 3-е изд. — Харьков, 1974. — С. 449—451.
Функция вида , где
называется квадратичной функцией.
График квадратичной функции – парабола.
Рассмотрим случаи:
I СЛУЧАЙ, КЛАССИЧЕСКАЯ ПАРАБОЛА
, то есть
,
,
Для построения заполняем таблицу, подставляя значения x в формулу:
Отмечаем точки (0;0); (1;1); (-1;1) и т.д. на координатной плоскости (чем с меньшим шагом мы берем значения х ( в данном случае шаг 1 ), и чем больше берем значений х, тем плавнее будет кривая), получаем параболу:
Нетрудно заметить, что если мы возьмем случай ,
,
, то есть
, то мы получим параболу, симметричную
относительно оси (ох). Убедиться в этом несложно, заполнив аналогичную таблицу:
II СЛУЧАЙ, «a» ОТЛИЧНО ОТ ЕДИНИЦЫ
Что же будет, если мы будем брать ,
,
? Как изменится поведение параболы? При
парабола
изменит форму, она “похудеет” по сравнению с параболой
(не верите – заполните соответствующую таблицу – и убедитесь сами):
На первой картинке (см. выше) хорошо видно, что точки из таблицы для параболы (1;1), (-1;1) трансформировались в точки (1;4), (1;-4), то есть при тех же значениях
ордината
каждой точки умножилась на 4. Это произойдет со всеми ключевыми точками исходной таблицы. Аналогично рассуждаем в случаях картинок 2 и 3.
А при парабола
«станет шире» параболы
:
Давайте подитожим:
III СЛУЧАЙ, ПОЯВЛЯЕТСЯ «С»
Теперь давайте введем в игру (то есть рассматриваем случай, когда
), будем рассматривать параболы вида
. Нетрудно догадаться (вы всегда можете обратиться к таблице), что будет происходить смещение параболы
вдоль оси
вверх или вниз в зависимости от знака
:

IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»
Когда же парабола “оторвется” от оси и будет, наконец, “гулять” по всей координатной плоскости? Когда
перестанет быть равным
.
Здесь для построения параболы нам понадобится формула для вычисления вершины:
,
.
Так вот в этой точке (как в точке (0;0) новой системы координат) мы будем строить параболу , что уже нам по силам. Если имеем дело со случаем
, то от вершины откладываем один единичный отрезок вправо, один вверх, – полученная точка – наша (аналогично шаг влево, шаг вверх – наша точка); если имеем дело с
, например, то от вершины откладываем один единичный отрезок вправо, два – вверх и т.д.
Например, вершина параболы :
,
. Теперь главное уяснить, что в этой вершине мы будем строить параболу по шаблону параболы
, ведь
в нашем случае.
При построении параболы после нахождения координат вершины очень удобно учитывать следующие моменты:
1) парабола обязательно пройдет через точку . Действительно, подставив в формулу
x=0, получим, что
. То есть ордината точки пересечения параболы с осью (оу), это
. В нашем примере (выше), парабола пересекает ось ординат в точке
, так как
.
2) осью симметрии параболы является прямая , поэтому все точки параболы будут симметричны относительно нее. В нашем примере, мы сразу берем точку (0; -2) и строим ей симметричную относительно оси симметрии параболы, получим точку (4; -2), через которую будет проходить парабола.
3) Приравнивая к
, мы узнаем точки пересечения параболы с осью (ох). Для этого решаем уравнение
. В зависимости от дискриминанта, будем получать одну (
,
), две (
,
) или нИсколько (
) точек пересечения с осью (ох). В предыдущем примере у нас корень из дискриминанта – не целое число, при построении нам особо нет смысла находить корни, но мы видим четко, что две точки пересечения с осью (ох) у нас будут (так как
), хотя, в общем, это видно и без дискриминанта.
Итак, давайте выработаем
Алгоритм для построения параболы, если она задана в виде 
1) определяем направление ветвей ( а>0 – вверх, a<0 – вниз)
2) находим координаты вершины параболы по формуле
,
.
3) находим точку пересечения параболы с осью (оу) по свободному члену , строим точку, симметричную данной относительно оси симметрии параболы (надо заметить, бывает, что эту точку невыгодно отмечать, например, потому, что значение
велико… пропускаем этот пункт…)
4) В найденной точке – вершине параболы (как в точке (0;0) новой системы координат) строим параболу . Если
, то парабола
становится у’же по сравнению с
, если
, то парабола расширяется по сравнению с
5) Находим точки пересечения параболы с осью (оу) (если они еще сами “не всплыли”), решая уравнение
Пример 1
Пример 2
Замечание 1. Если же парабола изначально нам задана в виде , где
– некоторые числа (например,
), то построить ее будет еще легче, потому что нам уже заданы координаты вершины
. Почему?
Возьмем квадратный трехчлен и выделим в нем полный квадрат:
Посмотрите, вот мы и получили, что
,
. Мы с вами ранее называли вершину параболы
, то есть теперь
,
.
Например, . Отмечаем на плоскости вершину параболы
, понимаем, что ветви направлены вниз, парабола расширена (относительно
). То есть выполняем пункты 1; 3; 4; 5 из алгоритма построения параболы (см. выше).
Замечание 2. Если парабола задана в виде, подобном этому (то есть
представлен в виде произведения двух линейных множителей), то нам сразу видны точки пересечения параболы с осью (ох). В данном случае – (0;0) и (4;0). В остальном же действуем согласно алгоритму, раскрыв скобки.
Функция вида y=ax2+bx+c, где а, b, с – некоторые числа, причем, а≠0 число, х – переменная, называется квадратичной функцией.
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.
Рисунок №1.
Вершина параболы. Формула.
Чтобы найти координаты вершины параболы (х0; у0), надо воспользоваться формулой:
х0=−b2a
для нахождения у0 можно просто подставить значение х0 в формулу данной функции y0=ax2+bx+c вместо х.
Рассмотрим это на примере конкретно заданной функции.
Пример №1
Найти вершину параболы, заданной формулой у=2х2 – 8х + 5.
Найдем, чему равны коэффициенты: а=2; b= – 8
Подставим их в формулу и вычислим значение х0:
х0=−b2a=82∙2=84=2
Теперь в заданную по условию формулу вместо х подставим найденное значение у0=2∙22 – 8∙2 + 5=8 – 16 + 5= –3
Итак, мы нашли координаты вершины параболы: (2; –3).
Ответ: (2; –3).
Нули параболы
Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.
Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.
Пример №2
Найти нули функции у=х2 +4х – 5
Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:
х2 +4х – 5=0
а=1, b=4, с= –5
D=b2 – 4ac=42 – 4∙1∙(−5)=36
x=−b±√D2a
x=−4±√362; х1=–5; х2=1
Значит, нули функции равны –5 и 1
Ответ: –5 и 1
Примечание к заданию по нахождению нулей функции без графика
Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).
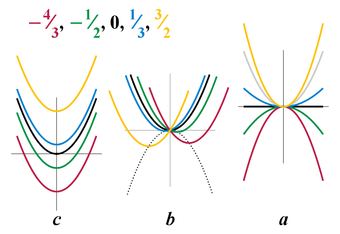
Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.
Пример №3
Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.
Теперь можно выполнить соответствие:
Ответ: 231
Пример №4
Рассмотрим еще пример на соответствие
В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х0.
Итак, найдем х0 для формулы «Б»:
х0=−b2a=−42∙2=−44=−1
Видим, что х0 отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.
Запишем в таблицу
Ответ: 231
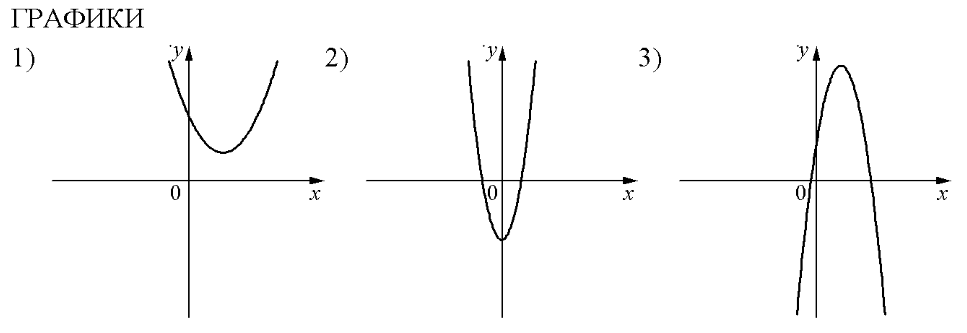
Задание 11OM21R
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Решение
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 – это график №1
Б) а<0; с>0 – это график №3
В) а>0, с<0 – это график №2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор
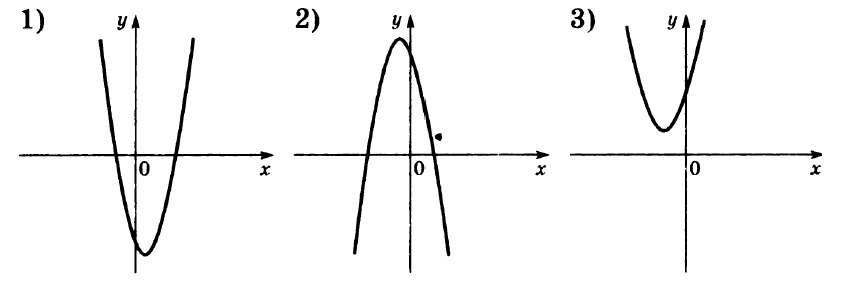
Задание OM1105o
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: 123
pазбирался: Даниил Романович | обсудить разбор
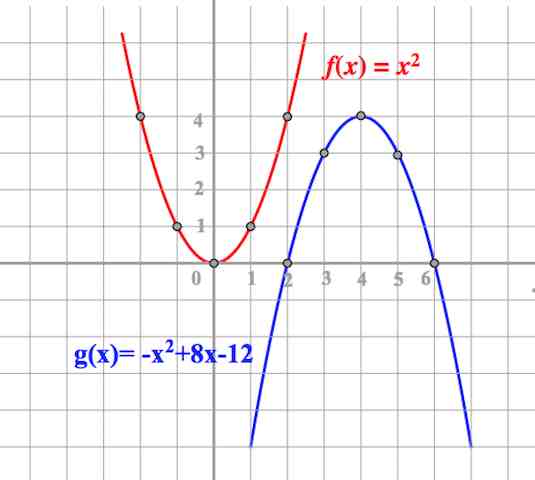
Задание OM1101o
На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Ответ: 321
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 10.7k




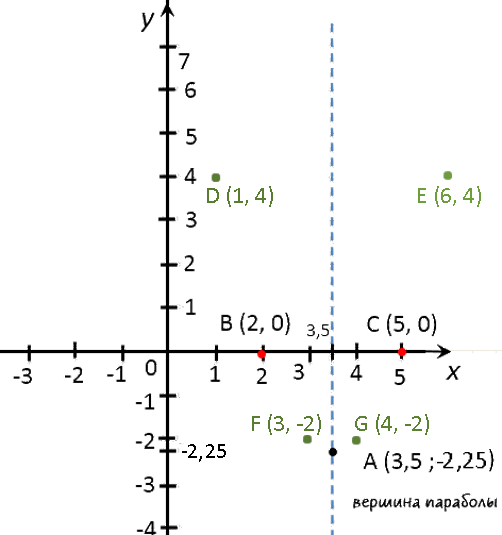


































































































![{displaystyle (-infty ;-2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/615ae99698f85cb43b3de7eb156149152b51acc6)