ПОИСК В СЛОВАРЯХ:
Морфемный разбор слова «сравним»
сравним
| сравн | — корень |
| им | — окончание |
| сравн | — основа слова |
См. тж.: сравнить, сравни, сравнив, сравнивши, сравнил, сравнила, сравнили, сравнило, сравнит, сравните, сравнишь, сравню, сравнят.
Разбор по составу слова: «сравним» — форма прилагательного «сравнимый» [кр. ф., м.р., ед.ч.] —
сравним
|
||||||||
| Морфемно-орфографический словарь сайта udarenieru.ru, 2014-2023. |
|---|
См. тж.: сравнимый, сравнимая, сравнимое, сравнимые, сравнимого, сравнимой, сравнимых, сравнимому, сравнимым, сравнимую, сравнимыми, сравнимом, сравнима, сравнимо, сравнимы, сравнимее, сравнимою, сравнимей.
Факт 1.
(bullet) Возьмем некоторое неотрицательное число (a) (то есть (ageqslant 0)). Тогда (арифметическим) квадратным корнем из числа (a) называется такое неотрицательное число (b), при возведении которого в квадрат мы получим число (a): [sqrt a=bquad text{то же самое, что }quad a=b^2] Из определения следует, что (ageqslant 0, bgeqslant 0). Эти ограничения являются важным условием существования квадратного корня и их следует запомнить!
Вспомним, что любое число при возведении в квадрат дает неотрицательный результат. То есть (100^2=10000geqslant 0) и ((-100)^2=10000geqslant 0).
(bullet) Чему равен (sqrt{25})? Мы знаем, что (5^2=25) и ((-5)^2=25). Так как по определению мы должны найти неотрицательное число, то (-5) не подходит, следовательно, (sqrt{25}=5) (так как (25=5^2)).
Нахождение значения (sqrt a) называется извлечением квадратного корня из числа (a), а число (a) называется подкоренным выражением.
(bullet) Исходя из определения, выражения (sqrt{-25}), (sqrt{-4}) и т.п. не имеют смысла.
Факт 2.
Для быстрых вычислений полезно будет выучить таблицу квадратов натуральных чисел от (1) до (20): [begin{array}{|ll|}
hline
1^2=1 & quad11^2=121 \
2^2=4 & quad12^2=144\
3^2=9 & quad13^2=169\
4^2=16 & quad14^2=196\
5^2=25 & quad15^2=225\
6^2=36 & quad16^2=256\
7^2=49 & quad17^2=289\
8^2=64 & quad18^2=324\
9^2=81 & quad19^2=361\
10^2=100& quad20^2=400\
hline end{array}]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
(bullet) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть [sqrt apmsqrt bne sqrt{apm b}] Таким образом, если вам нужно вычислить, например, (sqrt{25}+sqrt{49}), то первоначально вы должны найти значения (sqrt{25}) и (sqrt{49}), а затем их сложить. Следовательно, [sqrt{25}+sqrt{49}=5+7=12] Если значения (sqrt a) или (sqrt b) при сложении (sqrt
a+sqrt b) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме (sqrt
2+ sqrt {49}) мы можем найти (sqrt{49}) – это (7), а вот (sqrt
2) никак преобразовать нельзя, поэтому (sqrt 2+sqrt{49}=sqrt
2+7). Дальше это выражение, к сожалению, упростить никак нельзя
(bullet) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть [sqrt acdot sqrt b=sqrt{ab}quad text{и}quad
sqrt a:sqrt b=sqrt{a:b}] (при условии, что обе части равенств имеют смысл)
Пример: (sqrt{32}cdot sqrt 2=sqrt{32cdot
2}=sqrt{64}=8);
(sqrt{768}:sqrt3=sqrt{768:3}=sqrt{256}=16);
(sqrt{(-25)cdot (-64)}=sqrt{25cdot 64}=sqrt{25}cdot sqrt{64}=
5cdot 8=40).
(bullet) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем (sqrt{44100}). Так как (44100:100=441), то (44100=100cdot 441). По признаку делимости число (441) делится на (9) (так как сумма его цифр равна 9 и делится на 9), следовательно, (441:9=49), то есть (441=9cdot 49).
Таким образом, мы получили: [sqrt{44100}=sqrt{9cdot 49cdot 100}=
sqrt9cdot sqrt{49}cdot sqrt{100}=3cdot 7cdot 10=210] Рассмотрим еще один пример: [sqrt{dfrac{32cdot 294}{27}}=
sqrt{dfrac{16cdot 2cdot 3cdot 49cdot 2}{9cdot 3}}= sqrt{
dfrac{16cdot4cdot49}{9}}=dfrac{sqrt{16}cdot sqrt4 cdot
sqrt{49}}{sqrt9}=dfrac{4cdot 2cdot 7}3=dfrac{56}3]
(bullet) Покажем, как вносить числа под знак квадратного корня на примере выражения (5sqrt2) (сокращенная запись от выражения (5cdot
sqrt2)). Так как (5=sqrt{25}), то [5sqrt2=sqrt{25}cdot sqrt2=sqrt{25cdot 2}=sqrt{50}] Заметим также, что, например,
1) (sqrt2+3sqrt2=4sqrt2),
2) (5sqrt3-sqrt3=4sqrt3)
3) (sqrt a+sqrt a=2sqrt a).
Почему так? Объясним на примере 1). Как вы уже поняли, как-то преобразовать число (sqrt2) мы не можем. Представим, что (sqrt2) – это некоторое число (a). Соответственно, выражение (sqrt2+3sqrt2) есть не что иное, как (a+3a) (одно число (a) плюс еще три таких же числа (a)). А мы знаем, что это равно четырем таким числам (a), то есть (4sqrt2).
Факт 4.
(bullet) Часто говорят “нельзя извлечь корень”, когда не удается избавиться от знака (sqrt {} ) корня (радикала) при нахождении значения какого-то числа. Например, извлечь корень из числа (16) можно, потому что (16=4^2), поэтому (sqrt{16}=4). А вот извлечь корень из числа (3), то есть найти (sqrt3), нельзя, потому что нет такого числа, которое в квадрате даст (3).
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа (sqrt3, 1+sqrt2, sqrt{15}) и т.п. являются иррациональными.
Также иррациональными являются числа (pi) (число “пи”, приблизительно равное (3,14)), (e) (это число называют числом Эйлера, приблизительно оно равно (2,7)) и т.д.
(bullet) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой (mathbb{R}).
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
(bullet) Модуль вещественного числа (a) – это неотрицательное число (|a|), равное расстоянию от точки (a) до (0) на вещественной прямой. Например, (|3|) и (|-3|) равны 3, так как расстояния от точек (3) и (-3) до (0) одинаковы и равны (3). 
(bullet) Если (a) – неотрицательное число, то (|a|=a).
Пример: (|5|=5); (qquad |sqrt2|=sqrt2).
(bullet) Если (a) – отрицательное число, то (|a|=-a).
Пример: (|-5|=-(-5)=5); (qquad |-sqrt3|=-(-sqrt3)=sqrt3).
Говорят, что у отрицательных чисел модуль “съедает” минус, а положительные числа, а также число (0), модуль оставляет без изменений.
НО такое правило годится только для чисел. Если у вас под знаком модуля находится неизвестная (x) (или какая-то другая неизвестная), например, (|x|), про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля мы не можем. В этом случае это выражение таким и остается: (|x|).
(bullet) Имеют место следующие формулы: [{large{sqrt{a^2}=|a|}}] [{large{(sqrt{a})^2=a}},
text{ при условии } ageqslant 0] Очень часто допускается такая ошибка: говорят, что (sqrt{a^2}) и ((sqrt a)^2) – одно и то же. Это верно только в том случае, когда (a) – положительное число или ноль. А вот если (a) – отрицательное число, то это неверно. Достаточно рассмотреть такой пример. Возьмем вместо (a) число (-1). Тогда (sqrt{(-1)^2}=sqrt{1}=1), а вот выражение ((sqrt {-1})^2) вообще не существует (ведь нельзя под знак корня помещать отрицательные числа!).
Поэтому обращаем ваше внимание на то, что (sqrt{a^2}) не равен ((sqrt a)^2)!
Пример: 1) (sqrt{left(-sqrt2right)^2}=|-sqrt2|=sqrt2), т.к. (-sqrt2<0);
(phantom{00000}) 2) ((sqrt{2})^2=2).
(bullet) Так как (sqrt{a^2}=|a|), то [sqrt{a^{2n}}=|a^n|] (выражение (2n) обозначает четное число)
То есть при извлечении корня из числа, находящегося в какой-то степени, эта степень уменьшается в два раза.
Пример:
1) (sqrt{4^6}=|4^3|=4^3=64)
2) (sqrt{(-25)^2}=|-25|=25) (заметим, что если модуль не поставить, то получится, что корень из числа равен (-25); но мы помним, что по определению корня такого быть не может: у нас всегда при извлечении корня должно получаться положительное число или ноль)
3) (sqrt{x^{16}}=|x^8|=x^8) (так как любое число в четной степени неотрицательно)
Факт 6.
Как сравнить два квадратных корня?
(bullet) Для квадратных корней верно: если (sqrt a<sqrt b), то (a<b); если (sqrt a=sqrt b), то (a=b).
Пример:
1) сравним (sqrt{50}) и (6sqrt2). Для начала преобразуем второе выражение в (sqrt{36}cdot sqrt2=sqrt{36cdot 2}=sqrt{72}). Таким образом, так как (50<72), то и (sqrt{50}<sqrt{72}). Следовательно, (sqrt{50}<6sqrt2).
2) Между какими целыми числами находится (sqrt{50})?
Так как (sqrt{49}=7), (sqrt{64}=8), а (49<50<64), то (7<sqrt{50}<8), то есть число (sqrt{50}) находится между числами (7) и (8).
3) Сравним (sqrt 2-1) и (0,5). Предположим, что (sqrt2-1>0,5): [begin{aligned}
&sqrt 2-1>0,5 big| +1quad text{(прибавим единицу к обеим
частям)}\[1ex]
&sqrt2>0,5+1 big| ^2 quadtext{(возведем обе части в
квадрат)}\[1ex]
&2>1,5^2\
&2>2,25 end{aligned}] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и (sqrt 2-1<0,5).
Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве (-3<sqrt2) нельзя (убедитесь в этом сами)!
(bullet) Следует запомнить, что [begin{aligned}
&sqrt 2approx 1,4\[1ex]
&sqrt 3approx 1,7 end{aligned}] Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
(bullet) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. Покажем, как это работает, на примере.
Возьмем (sqrt{28224}). Мы знаем, что (100^2=10,000), (200^2=40,000) и т.д. Заметим, что (28224) находится между (10,000) и (40,000). Следовательно, (sqrt{28224}) находится между (100) и (200).
Теперь определим, между какими “десятками” находится наше число (то есть, например, между (120) и (130)). Также из таблицы квадратов знаем, что (11^2=121), (12^2=144) и т.д., тогда (110^2=12100), (120^2=14400), (130^2=16900), (140^2=19600), (150^2=22500), (160^2=25600), (170^2=28900). Таким образом, мы видим, что (28224) находится между (160^2) и (170^2). Следовательно, число (sqrt{28224}) находится между (160) и (170).
Попробуем определить последнюю цифру. Давайте вспомним, какие однозначные числа при возведении в квадрат дают на конце (4)? Это (2^2) и (8^2). Следовательно, (sqrt{28224}) будет заканчиваться либо на 2, либо на 8. Проверим это. Найдем (162^2) и (168^2):
(162^2=162cdot 162=26224)
(168^2=168cdot 168=28224).
Следовательно, (sqrt{28224}=168). Вуаля!
Как сравнивать корни
Корнем n-ой степени из действительного числа a называется такое число b, для которого выполняется равенство b^n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени – только для положительных. Значением корня часто является бесконечная десятичная дробь, что затрудняет его точное вычисление, поэтому важно уметь сравнивать корни.

Инструкция
Пусть требуется сравнить два иррациональных числа. Первое, на что следует обратить внимание – это показатели степени корней у сравниваемых чисел. Если показатели одинаковы, то сравнивают подкоренные выражения. Очевидно, что чем больше подкоренное число, тем больше значение корня при равных показателях. Например, пусть надо сравнить кубический корень из двух и кубический корень из восьми. Показатели одинаковы и равны 3, подкоренные выражения 2 и 8, причем 2 < 8. Следовательно, и кубический корень из двух меньше кубического корня из восьми.
В другом случае показатели степени могут быть разными, а подкоренные выражения одинаковыми. Тоже вполне понятно, что при извлечении корня большей степени получится меньшее число.Возьмите для примера кубический корень из восьми и корень шестой степени из восьми. Если обозначить значение первого корня как a, а второго – как b, то a^3 = 8 и b^6 = 8. Легко видеть, что a должно быть больше b, таким образом кубический корень из восьми больше корня шестой степени из восьми.
Более сложной представляется ситуация с разными показателями степени корня и разными подкоренными выражениями. В таком случае надо найти наименьшее общее кратное для показателей корней и возвести оба выражения в степень, равную наименьшему общему кратному.Пример: надо сравнить 3^1/3 и 2^1/2 (математическая запись корней есть на рисунке). Наименьшее общее кратное для 2 и 3 равно 6. Возведите оба корня в шестую степень. Тут же получится, что 3^2 = 9 и 2^3 = 8, 9 > 8. Следовательно, и 3^1/3 > 2^1/2.
Полезный совет
Чтобы сравнить арифметические выражения, состоящие из нескольких корней, придется их приводить к общему корню. Это можно сделать, пользуясь формулами сокращенного умножения, формулой Бинома Ньютона и другими приемами.
Источники:
- Преобразования выражений, включающих корни натуральной степени
- кубический корень из 2
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Методические рекомендации к практической работе по математике на тему «Вычисление и сравнение корней»»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Практическое занятие
Тема: Вычисление и сравнение корней
Методические указания.
Чтобы успешно использовать на практике операцию извлечения корня, нужно знать свойства этой операции.
Арифметическим корнем n-ой степени из неотрицательного числа а называется неотрицательное число, n-ая степень которого равна а .
Свойства корня n -й степени:
При сравнении иррациональных чисел:
Первое, на что следует обратить внимание — это показатели степени корней у сравниваемых чисел. Если показатели одинаковы, то сравнивают подкоренные выражения. Очевидно, что чем больше подкоренное число, тем больше значение корня при равных показателях.
Например , пусть надо сравнить кубический корень из двух и кубический корень из восьми. Показатели одинаковы и равны 3, подкоренные выражения 2 и 8, причем 2<8. Следовательно, и кубический корень из двух меньше кубического корня из восьми.
В другом случае показатели степени могут быть разными, а подкоренные выражения одинаковыми. Тоже вполне понятно, что при извлечении корня большей степени получится меньшее число. Возьмите для примера кубический корень из восьми и корень шестой степени из восьми. Если обозначить значение первого корня как a , а второго — как b , то a 3 = 8 и b 6 = 8. Легко видеть, что a должно быть больше b , таким образом кубический корень из восьми больше корня шестой степени из восьми.
Более сложной представляется ситуация с разными показателями степени корня и разными подкоренными выражениями. В таком случае надо найти наименьшее общее кратное для показателей корней и возвести оба выражения в степень, равную наименьшему общему кратному.
Например: надо сравнить и . Наименьшее общее кратное для 2 и 3 равно 6. Возведите оба корня в шестую степень. Тут же получится, что 3 2 = 9 и 2 3 = 8, 9 > 8. Следовательно, > .
Контрольные вопросы
Что такое радикал?
Основное свойство корня?
Сформулируйте определение корня n -ой степени из неотрицательного числа.
Сформулируйте определение корня нечетной степени из отрицательного числа.
Что такое квадратный корень

Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:
Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.
Определение квадратного корня также можно представить в виде формул:
Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.
Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.
Попробуем найти корень из
Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.
Если — 4, то -4 * -4 = 16, (минус на минус всегда дает плюс).
Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.
Числа, стоящие под знаком корня, должны быть положительными.
Исходя из определения, значение корня также не должно быть отрицательным.
Здесь могут возникнуть резонные вопросы, почему, например, в примере , и .
Разница между квадратным корнем и арифметическим квадратным уравнением
Прежде всего, чтобы разграничить эти два понятия, запомните:
Это два нетождественных друг другу выражения.
— это квадратное уравнение.
— арифметический квадратный корень.
Из выражения следует, что:
Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.
В то же самое время, из выражения следует, что .
Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:
Пример решен неверно
Это квадратное уравнение.
Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.
Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.
Даны два выражения:
Первое выражение — квадратное уравнение.
Второе выражение — арифметический квадратный корень.
Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.
Запись иррациональных чисел с помощью квадратного корня
Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.
Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.
Примеры иррациональных чисел:
Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.
Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.
Переберем числа, чтобы удостовериться в этом:
Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.
Решение следующее:
Строим график функции y = x 2 .
Отмечаем решения на графике: .

Если попробовать извлечь квадратный корень из 2 с помощью калькулятора, то результат будет следующий: .
В таком виде ответ не записывают — нужно оставить квадратный корень.
Извлечение корней
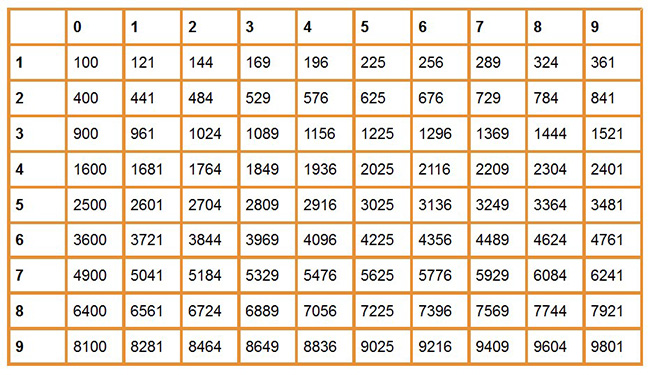
Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.
Таблица квадратов

Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:
- 1. Извлеките квадратный корень:
Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.
Влево — 1, вверх — 7.
- 2. Извлеките квадратный корень:
Ищем в таблице число 3025.
Влево — 5, вверх — 5.
- 3. Извлеките квадратный корень:
Ищем в таблице число 7396.
Влево — 8, вверх — 6.
- 4. Извлеките корень:
Ищем в таблице число 9025.
Влево — 9, вверх — 5.
- 5. Извлеките корень
Ищем в таблице число 1600.
Влево — 4, вверх — 0.
Извлечением корня называется нахождение его значение.
Свойства арифметического квадратного корня
У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.
Корень произведения равен произведению корней
Извлечь корень из дроби — это извлечь корень из числителя и из знаменателя
Чтобы возвести корень в степень, нужно возвести в степень значение под корнем
Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.
Умножение арифметических корней
Для умножения арифметических корней используйте формулу:
Примеры:
Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.
Если нет возможности извлечь корни из чисел, то поступаем так:
Если множителей больше двух, то решается примерно точно так, как и с двумя множителями:
Деление арифметических корней
Для деления арифметических корней используйте формулу:
Примеры:
Ответ: смешанную дробь превращаем в неправильную (16 * 3) + 1 = 49
Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.
Возведение арифметических корней в степень
Для возведения арифметического корня в степень используйте формулу:
Примеры:
Эти две формулы нужно запомнить:
Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.
Внесение множителя под знак корня
Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.
А теперь давайте разберемся, как вносить множитель под знак корня.
Число семь умножено на квадратный корень из числа девять.
Извлечем квадратный корень и умножим его на 7.
В данном выражение число 7 — множитель. Давайте внесем его под знак корня.
Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.
Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.
Формула внесения множителя под знак корня:
Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.
Вынесение множителя из-под знака корня
С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.
Дано выражение в виде квадратного корня из произведения.
Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.
Извлекаем корень из всех имеющихся множителей.
В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:
Таким образом множитель выносится из-под знака корня.
Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.
Раскладываем подкоренное выражение на множители 28 = 7*4.
Извлекаем корень из 4. Множитель 7 оставляем под знаком корня.
Ответ: по правилу извлечения квадратного корня из произведения,
Так как вынесенный множитель должен стоять перед подкоренным знаком, то меняем их местами.
Вынесите множитель из-под знака корня в выражении:
Ответ: Раскладываем выражение под корнем на множители 24 = 6 * 4.
Представим в виде
Представим в виде
Вынесем в двух последних выражения множитель из-под знака корня.
Умножаем . Все остальное выражение записываем в неизменном виде.
Мы видим, что во всем выражении есть один общий множитель — .
Выносим общий множитель за скобки:
Далее вычисляем все, что в скобках:
Сравнение квадратных корней
Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.
Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.
Если:
Давайте разберем на примере.
Сравните два выражения: и
Первым делом преобразуем второе выражение: .
Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.
Сравните два выражения: и
Ответ: преобразовываем выражение .
Сравните два выражения: и
Ответ: преобразовываем выражение .
Сравните два выражения: и
Ответ: преобразовываем выражение .
Как видите, ничего сложного в сравнении арифметических квадратных корней нет.
Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.
Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.
Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.
Таких калькуляторов в интернете много, вот один из них.
Извлечение квадратного корня из большого числа
Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.
Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:
Определить «сотни», между которыми оно стоит.
Определить «десятки», между которыми оно стоит.
Определить последнюю цифру в этом числе.
Извлечь корень из большого числа можно разными способами — вот один из них.
Извлечем корень из .
Наша задача в том, чтобы определить между какими десятками стоит число 2116.
Мы видим что, 2116 больше 1600, но меньше 2500.
Это значит, что число 2116 находится между 40 2 и 50 2 .
41, 42, 43, 44, 45, 46, 47, 48, 49.
Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.
Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей
4 2 = 16 ⇒ 6
5 2 = 25 ⇒ 5
6 2 = 36 ⇒ 6
7 2 = 49 ⇒ 9
8 2 = 64 ⇒ 4
9 2 = 81 ⇒ 1
Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.
Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.
Число 43, возведенное в квадрат, даст число, на конце которого — 9.
Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.
Таким образом, у нас остаются два варианта: 44 2 и 46 2 .
Далее вычисляем: 44 * 44 = 1936.
Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.
Квадратный корень. Действия с квадратными корнями. Модуль. Сравнение квадратных корней
Вы ищете теорию и формулы для ЕГЭ по математике ? Образовательный проект «Школково» предлагает вам заглянуть в раздел «Теоретическая справка». Здесь представлено пособие по подготовке к ЕГЭ по математике, которое фактически является авторским. Оно разработано в соответствии с программой школьного курса и включает такие разделы, как арифметика, алгебра, начала анализа и геометрия (планиметрия и стереометрия). Каждое теоретическое положение, содержащееся в пособии по подготовке к ЕГЭ по математике, сопровождается методически подобранными задачами с подробными разъяснениями.
Таким образом, вы не только приобретете определенные знания. Полный справочник для ЕГЭ по математике поможет вам научиться логически и нестандартно мыслить , выполнять самые разнообразные задачи и грамотно объяснять свои решения. А это уже половина успеха при сдаче единого государственного экзамена.
После того, как вы нашли необходимые формулы и теорию для ЕГЭ по математике, рекомендуем вам перейти в раздел «Каталоги» и закрепить полученные знания на практике. Для этого достаточно выбрать задачу по данной теме и решить ее. Кроме того, справочные материалы по математике для ЕГЭ пригодятся вам и для других естественнонаучных дисциплин, таких как физика, химия и т. д.
Факт 1.
(bullet) Возьмем некоторое неотрицательное число (a) (то есть (ageqslant 0) ). Тогда (арифметическим) квадратным корнем из числа (a) называется такое неотрицательное число (b) , при возведении которого в квадрат мы получим число (a) : [sqrt a=bquad textquad a=b^2] Из определения следует, что (ageqslant 0, bgeqslant 0) . Эти ограничения являются важным условием существования квадратного корня и их следует запомнить!
Вспомним, что любое число при возведении в квадрат дает неотрицательный результат. То есть (100^2=10000geqslant 0) и ((-100)^2=10000geqslant 0) .
(bullet) Чему равен (sqrt) ? Мы знаем, что (5^2=25) и ((-5)^2=25) . Так как по определению мы должны найти неотрицательное число, то (-5) не подходит, следовательно, (sqrt=5) (так как (25=5^2) ).
Нахождение значения (sqrt a) называется извлечением квадратного корня из числа (a) , а число (a) называется подкоренным выражением.
(bullet) Исходя из определения, выражения (sqrt) , (sqrt) и т.п. не имеют смысла.
Факт 2.
Для быстрых вычислений полезно будет выучить таблицу квадратов натуральных чисел от (1) до (20) : [beginhline 1^2=1 & quad11^2=121 \ 2^2=4 & quad12^2=144\ 3^2=9 & quad13^2=169\ 4^2=16 & quad14^2=196\ 5^2=25 & quad15^2=225\ 6^2=36 & quad16^2=256\ 7^2=49 & quad17^2=289\ 8^2=64 & quad18^2=324\ 9^2=81 & quad19^2=361\ 10^2=100& quad20^2=400\ hline end]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
(bullet) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть [sqrt apmsqrt bne sqrt] Таким образом, если вам нужно вычислить, например, (sqrt+sqrt) , то первоначально вы должны найти значения (sqrt) и (sqrt) , а затем их сложить. Следовательно, [sqrt+sqrt=5+7=12] Если значения (sqrt a) или (sqrt b) при сложении (sqrt a+sqrt b) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме (sqrt 2+ sqrt ) мы можем найти (sqrt) – это (7) , а вот (sqrt 2) никак преобразовать нельзя, поэтому (sqrt 2+sqrt=sqrt 2+7) . Дальше это выражение, к сожалению, упростить никак нельзя (bullet) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть [sqrt acdot sqrt b=sqrtquad textquad sqrt a:sqrt b=sqrt] (при условии, что обе части равенств имеют смысл)
Пример: (sqrtcdot sqrt 2=sqrt=sqrt=8) ; (sqrt:sqrt3=sqrt=sqrt=16) ; (sqrt=sqrt=sqrtcdot sqrt= 5cdot 8=40) . (bullet) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем (sqrt) . Так как (44100:100=441) , то (44100=100cdot 441) . По признаку делимости число (441) делится на (9) (так как сумма его цифр равна 9 и делится на 9), следовательно, (441:9=49) , то есть (441=9cdot 49) .
Таким образом, мы получили: [sqrt=sqrt= sqrt9cdot sqrtcdot sqrt=3cdot 7cdot 10=210] Рассмотрим еще один пример: [sqrt>= sqrt>= sqrt>=dfraccdot sqrt4 cdot sqrt>=dfrac3=dfrac3]
(bullet) Покажем, как вносить числа под знак квадратного корня на примере выражения (5sqrt2) (сокращенная запись от выражения (5cdot sqrt2) ). Так как (5=sqrt) , то [5sqrt2=sqrtcdot sqrt2=sqrt=sqrt] Заметим также, что, например,
1) (sqrt2+3sqrt2=4sqrt2) ,
2) (5sqrt3-sqrt3=4sqrt3)
3) (sqrt a+sqrt a=2sqrt a) .
Почему так? Объясним на примере 1). Как вы уже поняли, как-то преобразовать число (sqrt2) мы не можем. Представим, что (sqrt2) – это некоторое число (a) . Соответственно, выражение (sqrt2+3sqrt2) есть не что иное, как (a+3a) (одно число (a) плюс еще три таких же числа (a) ). А мы знаем, что это равно четырем таким числам (a) , то есть (4sqrt2) .
Факт 4.
(bullet) Часто говорят “нельзя извлечь корень”, когда не удается избавиться от знака (sqrt ) корня (радикала) при нахождении значения какого-то числа. Например, извлечь корень из числа (16) можно, потому что (16=4^2) , поэтому (sqrt=4) . А вот извлечь корень из числа (3) , то есть найти (sqrt3) , нельзя, потому что нет такого числа, которое в квадрате даст (3) .
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа (sqrt3, 1+sqrt2, sqrt) и т.п. являются иррациональными.
Также иррациональными являются числа (pi) (число “пи”, приблизительно равное (3,14) ), (e) (это число называют числом Эйлера, приблизительно оно равно (2,7) ) и т.д.
(bullet) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой (mathbb) .
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
(bullet) Модуль вещественного числа (a) – это неотрицательное число (|a|) , равное расстоянию от точки (a) до (0) на вещественной прямой. Например, (|3|) и (|-3|) равны 3, так как расстояния от точек (3) и (-3) до (0) одинаковы и равны (3) . 
(bullet) Если (a) – неотрицательное число, то (|a|=a) .
Пример: (|5|=5) ; (qquad |sqrt2|=sqrt2) . (bullet) Если (a) – отрицательное число, то (|a|=-a) .
Пример: (|-5|=-(-5)=5) ; (qquad |-sqrt3|=-(-sqrt3)=sqrt3) .
Говорят, что у отрицательных чисел модуль “съедает” минус, а положительные числа, а также число (0) , модуль оставляет без изменений.
НО такое правило годится только для чисел. Если у вас под знаком модуля находится неизвестная (x) (или какая-то другая неизвестная), например, (|x|) , про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля мы не можем. В этом случае это выражение таким и остается: (|x|) . (bullet) Имеют место следующие формулы: [=|a|>>] [>, text ageqslant 0] Очень часто допускается такая ошибка: говорят, что (sqrt) и ((sqrt a)^2) – одно и то же. Это верно только в том случае, когда (a) – положительное число или ноль. А вот если (a) – отрицательное число, то это неверно. Достаточно рассмотреть такой пример. Возьмем вместо (a) число (-1) . Тогда (sqrt=sqrt=1) , а вот выражение ((sqrt )^2) вообще не существует (ведь нельзя под знак корня помещать отрицательные числа!).
Поэтому обращаем ваше внимание на то, что (sqrt) не равен ((sqrt a)^2) ! Пример: 1) (sqrt=|-sqrt2|=sqrt2) , т.к. (-sqrt2<0) ;
(phantom) 2) ((sqrt)^2=2) . (bullet) Так как (sqrt=|a|) , то [sqrt>=|a^n|] (выражение (2n) обозначает четное число)
То есть при извлечении корня из числа, находящегося в какой-то степени, эта степень уменьшается в два раза.
Пример:
1) (sqrt=|4^3|=4^3=64)
2) (sqrt=|-25|=25) (заметим, что если модуль не поставить, то получится, что корень из числа равен (-25) ; но мы помним, что по определению корня такого быть не может: у нас всегда при извлечении корня должно получаться положительное число или ноль)
3) (sqrt>=|x^8|=x^8) (так как любое число в четной степени неотрицательно)
Факт 6.
Как сравнить два квадратных корня?
(bullet) Для квадратных корней верно: если (sqrt a<sqrt b) , то (a<b) ; если (sqrt a=sqrt b) , то (a=b) .
Пример:
1) сравним (sqrt) и (6sqrt2) . Для начала преобразуем второе выражение в (sqrtcdot sqrt2=sqrt=sqrt) . Таким образом, так как (50<72) , то и (sqrt<sqrt) . Следовательно, (sqrt<6sqrt2) .
2) Между какими целыми числами находится (sqrt) ?
Так как (sqrt=7) , (sqrt=8) , а (49<50<64) , то (7<sqrt<8) , то есть число (sqrt) находится между числами (7) и (8) .
3) Сравним (sqrt 2-1) и (0,5) . Предположим, что (sqrt2-1>0,5) : [begin &sqrt 2-1>0,5 big| +1quad text\[1ex] &sqrt2>0,5+1 big| ^2 quadtext\[1ex] &2>1,5^2\ &2>2,25 end] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и (sqrt 2-1<0,5) .
Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве (-3<sqrt2) нельзя (убедитесь в этом сами)! (bullet) Следует запомнить, что [begin &sqrt 2approx 1,4\[1ex] &sqrt 3approx 1,7 end] Знание приблизительного значения данных чисел поможет вам при сравнении чисел! (bullet) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. Покажем, как это работает, на примере.
Возьмем (sqrt) . Мы знаем, что (100^2=10,000) , (200^2=40,000) и т.д. Заметим, что (28224) находится между (10,000) и (40,000) . Следовательно, (sqrt) находится между (100) и (200) .
Теперь определим, между какими “десятками” находится наше число (то есть, например, между (120) и (130) ). Также из таблицы квадратов знаем, что (11^2=121) , (12^2=144) и т.д., тогда (110^2=12100) , (120^2=14400) , (130^2=16900) , (140^2=19600) , (150^2=22500) , (160^2=25600) , (170^2=28900) . Таким образом, мы видим, что (28224) находится между (160^2) и (170^2) . Следовательно, число (sqrt) находится между (160) и (170) .
Попробуем определить последнюю цифру. Давайте вспомним, какие однозначные числа при возведении в квадрат дают на конце (4) ? Это (2^2) и (8^2) . Следовательно, (sqrt) будет заканчиваться либо на 2, либо на 8. Проверим это. Найдем (162^2) и (168^2) :
(162^2=162cdot 162=26224)
(168^2=168cdot 168=28224) .
Следовательно, (sqrt=168) . Вуаля!
Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор . Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.
- Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.
Например, нам необходимо сравнить две дроби: ( 1,6) и ( 1frac{6}{13}).
Давай разберем каждый вариант
Вариант 1. Сравнение дробей с помощью приведения к общему знаменателю
Запишем ( 1,6) в виде обыкновенной дроби:
( 1,6=1frac{6}{10}=1frac{3}{5}) — (как ты видишь, я также сократила на ( 2) числитель и знаменатель).
Теперь нам необходимо сравнить дроби:
( 1frac{3}{5}) и ( 1frac{6}{13})
Сейчас мы можем продолжить сравнивать также двумя способами. Мы можем:
Способ 1. Числитель больше знаменателя
Просто приведите все к общему знаменателю, представив обе дроби как неправильные (числитель больше знаменателя):
( frac{8}{5}vee frac{19}{13})
( frac{8cdot 13}{5cdot 13}vee frac{19cdot 5}{13cdot 5})
( frac{104}{65}vee frac{95}{65})
Какое число больше? Правильно, то, у которого числитель больше, то есть первое.
( 1,6>1frac{6}{13})
Способ 2. Отбросьте единицу
«Отбросьте» ( 1) (считай, что мы из каждой дроби вычли единицу, и соотношение дробей друг с другом, соответственно, не изменилось) и будем сравнивать дроби:
( frac{3}{5}vee frac{6}{13})
Приводим их также к общему знаменателю:
( frac{3cdot 13}{13cdot 5}vee frac{6cdot 5}{13cdot 5})
Заметь, в принципе мы можем не считать знаменатель. Мы итак видим, что он одинаков и нам необходимо сравнивать числитель. Тогда зачем мы будем тратить время на подсчет знаменателя?
( frac{39}{13cdot 5}vee frac{30}{13cdot 5})
Мы получили абсолютно точно такой же результат, как и в предыдущем случае – первое число больше, чем второе:
( 1,6>1frac{6}{13})
Проверим также, правомерно ли мы вычли единицу? Посчитаем разницу в числителе при первом расчете и втором:
1) ( 104-95=9)
2) ( 39-30=9)
Итак, мы рассмотрели, как сравнивать дроби, приводя их к общему знаменателю. Перейдем к другому методу – сравнение дробей приводя их к общему… числителю.
Вариант 2. Сравнение дробей с помощью приведения к общему числителю
Да, да. Это не опечатка. В школе редко кому рассказывают этот метод, но очень часто он весьма удобен. Чтобы ты быстро понял его суть, задам тебе только один вопрос – «в каких случаях значение дроби наибольшее?»
Конечно, ты скажешь «когда числитель максимально большой, а знаменатель максимально маленький».
Например, ты же точно скажешь, что ( frac{8}{13}<frac{12}{13}) Верно?
А если нам надо сравнить такие дроби: ( frac{6}{13}vee frac{6}{28})?
Думаю, ты тоже сразу верно поставишь знак, ведь в первом случае ( 6) делят на ( 13) частей, а во втором на целых ( 28), значит, во втором случае кусочки получаются совсем маленькие, и соответственно: ( frac{6}{13}>frac{6}{28}).
Как ты видишь, знаменатели здесь разные, а вот числители одинаковы. Однако, для того, чтобы сравнить эти две дроби, тебе не обязательно искать общий знаменатель. Хотя… найди его и посмотри, вдруг знак сравнения все же неправильный?
( frac{6cdot 28}{13cdot 28}>frac{6cdot 13}{28cdot 13})
( frac{168}{364}>frac{78}{364})
А знак-то тот же.
Вернемся к нашему изначальному заданию – сравнить ( 1frac{3}{5})и ( 1frac{6}{13}). Будем сравнивать ( frac{3}{5}) и ( frac{6}{13}).
Приведем данные дроби не к общему знаменателю, а к общему числителю.
Для этого просто числитель и знаменатель первой дроби умножим на ( 2). Получим:
( frac{6}{10}) и ( frac{6}{13}).
Какая дробь больше? Правильно, первая.
Вариант 3. Сравнение дробей с помощью вычитания
Как сравнивать дроби с помощью вычитания? Да очень просто.
Мы из одной дроби вычитаем другую. Если результат получается положительным, то первая дробь (уменьшаемое) больше второй (вычитаемое), а если отрицательным, то наоборот.
В нашем случае попробуем из второй вычесть первую дробь: ( 1frac{6}{13}-1,6).
Как ты уже понял, мы так же переводим ( 1,6) в обыкновенную дробь и получаем тот же результат — ( 1frac{3}{5}) .
Наше выражение приобретает вид:
( 1frac{6}{13}-1frac{3}{5})
Далее нам все равно придется прибегнуть к приведению к общему знаменателю.
Вопрос как: первым способом, преобразуя дроби в неправильные, или вторым, как бы «убирая» единицу? Кстати, это действие имеет вполне математическое обоснование. Смотри:
( left( 1+frac{6}{13} right)-left( 1+frac{3}{5} right)=1+frac{6}{13}-1-frac{3}{5}=frac{6}{13}-frac{3}{5})
Мне больше нравится второй вариант, так как перемножение в числителе при приведении к общему знаменателю становится в разы проще.
Приводим к общему знаменателю:
( frac{6}{13}-frac{3}{5}=frac{6cdot 5}{13cdot 5}-frac{3cdot 13}{5cdot 13}=frac{30}{13cdot 5}-frac{39}{5cdot 13}=-frac{9}{5cdot 13})
Здесь главное не запутаться, какое число и откуда мы отнимали. Внимательно посмотреть ход решения и случайно не перепутать знаки. Мы отнимали от второго числа первое и получили отрицательный ответ, значит?..
Правильно, первое число больше второго.
( 1,6>1frac{6}{13})
Вариант 5. Сравнение дробей с помощью деления
Да, да. И так тоже можно.
Логика проста: когда мы делим большее число на меньшее, в ответе у нас получается число, больше единицы, а если мы делим меньшее число на большее, то ответ приходится на промежуток от ( 0) до ( 1).
Чтобы запомнить это правило, возьми для сравнения любые два простых числа, например, ( 6) и ( 4). Ты же знаешь, что ( 6) больше ( 4)?
Теперь разделим ( 6) на ( 4). Наш ответ — ( 1,5). Соответственно, теория верна.
Если мы разделим ( displaystyle 4) на ( 6), что мы получим ( 0,left( 6 right)) – меньше единицы, что в свою очередь подтверждает, что ( displaystyle 4) на самом деле меньше ( 6).
Попробуем применить это правило на обыкновенных дробях. Сравним:
( frac{6}{8}vee frac{10}{12})
Разделим первую дробь на вторую:
( frac{6}{8}:frac{10}{12}=frac{6}{8}cdot frac{12}{10})
Сократим на ( 2) и на ( 4).
( frac{6}{8}cdot frac{12}{10}=frac{3}{2}cdot frac{3}{5}=frac{9}{10})
Полученный результат меньше ( 1), значит делимое меньше делителя, то есть:
( frac{6}{8}<frac{10}{12})
Мы разобрали все возможные варианты сравнения дробей. Как мы и говорили их пять.
Сравнение степеней
Теперь представим, что нам необходимо сравнить не просто числа, а выражения, где существует степень (читай раздел про степени).
Cравни: ( {{2}^{4}}vee {{2}^{6}}).
Конечно, ты без труда поставишь знак:
( {{2}^{4}}<{{2}^{6}}), ведь если мы заменим степень умножением, мы получим:
( 2cdot 2cdot 2cdot 2<2cdot 2cdot 2cdot 2cdot 2cdot 2)
Из этого маленького и примитивного примера вытекает правило:
Если основание сравниваемых степеней одинаково, то больше та степень, у которой больше показатель степени.
Попробуй теперь сравнить следующее: ( {{5}^{4}}vee {{6}^{4}}). Ты так же без труда поставишь знак:
( {{5}^{4}}<{{6}^{4}}), потому что, если мы заменим возведение степень на умножение…
В общем, ты все понял, и это совсем несложно.
Сложности возникают только тогда, когда при сравнении у степеней разные и основания, и показатели.
В этом случае необходимо попробовать привести к общему основанию. Например:
( {{2}^{2}}vee {{4}^{3}})
Разумеется, ты знаешь, что ( 4) это ( {{2}^{2}}), соответственно, выражение приобретает вид:
Раскроем скобки и сравним то, что получится:
( {{2}^{2}}vee {{2}^{6}}) — легко?
( {{2}^{2}}<{{2}^{6}})
Сравнение чисел с корнем
Для начала вспомним, что такое корни? Вот эту ( sqrt[n]{a}=b) запись помнишь?
( sqrt[n]{a}=b {{b}^{n}}=a)
Корнем ( n-ой) степени из действительного числа ( a) называется такое число ( b), для которого выполняется равенство ( {{b}^{n}}=a).
Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.
Значением корня часто является бесконечная десятичная дробь, что затрудняет его точное вычисление, поэтому важно уметь сравнивать корни.
Если ты подзабыл, что это такое и с чем его едят – почитай про корни здесь. Если все помнишь – давай учиться поэтапно сравнивать корни.
Допустим, нам необходимо сравнить:
( sqrt[3]{4}vee sqrt[3]{6})
Чтобы сравнить эти два корня, не нужно делать никаких вычислений, просто проанализируй само понятие «корень».
Понял, о чем я говорю?
Да вот об этом: ( sqrt[3]{4}vee sqrt[3]{6})иначе можно записать как третья степень какого-то числа, равна подкоренному выражению.
( {{x}^{3}}=4)
( {{y}^{3}}=6)
А что больше? ( y) или ( x)? Это ты, конечно, сравнишь без всякого труда. Чем большее число мы возводим в степень, тем больше будет значение.
Итак. Выведем правило.
Если показатели степени корней одинаковы (в нашем случае это ( 3)), то необходимо сравнивать подкоренные выражения (( 4) и ( 6)) — чем больше подкоренное число, тем больше значение корня при равных показателях.
Сложно запомнить? Тогда просто держи в голове пример ( sqrt{16}) и ( sqrt{4}). Что больше?
( sqrt{16}=4)
( sqrt{4}=2)
( 4) больше ( 2).
Показатели степени корней одинаковы, так как корень квадратный. Подкоренное выражение одного числа (( 16)) больше другого (( 4)), значит, правило действительно верное.
А что, если подкоренные выражения одинаковые, а вот степени корней разные? Например: ( sqrt[4]{6}vee sqrt[3]{6}).
Тоже вполне понятно, что при извлечении корня большей степени получится меньшее число. Возьмем для примера:
( sqrt[3]{12}vee sqrt[6]{12})
Обозначим значение первого корня как ( a), а второго — как ( b), то:
( {{a}^{3}}=12)
( {{b}^{6}}=12)
Ты без труда видишь, что в данных уравнениях ( a) должно быть больше ( b), следовательно:
( sqrt[3]{12}>sqrt[6]{12}).
Если подкоренные выражения одинаковы (в нашем случае ( 12)), а показатели степени корней различны (в нашем случае это ( 3) и ( 6)), то необходимо сравнивать показатели степени (( 3) и ( 6)) — чем больше показатель, тем меньше данное выражение.
Как избавляться от логарифмов
Как избавляться от логарифмов, подробно описано в теме «Логарифмические неравенства». Основные правила такие:
({log _a}x vee b{rm{ }} Leftrightarrow {rm{ }}left[ {begin{array}{*{20}{l}}{x vee {a^b};{rm{при}};a > 1}\{x wedge {a^b};{rm{при}};0 < a < 1}end{array}} right. ) или ( {log _a}x vee {log _a}y{rm{ }} Leftrightarrow {rm{ }}left[ {begin{array}{*{20}{l}}{x vee y;{rm{при}};a > 1}\{x wedge y;{rm{при}};0 < a < 1}end{array}} right. )
Также можем добавить правило про логарифмы с разными основаниями и одинаковым аргументом:
( displaystyle begin{array}{l}a>b>1 Leftrightarrow {{log }_{a}}x<{{log }_{b}}x\1>a>b>0 Leftrightarrow {{log }_{a}}x>{{log }_{b}}xend{array})
Объяснить его можно так: чем больше основание, тем в меньшую степень его придется возвести, чтобы получить один и тот же ( x). Если же основание меньше ( 1), то все наоборот, так как соответствующая функция монотонно убывающая.
Пример.
Сравните числа: ( {{log }_{3}}5) и ( {{log }_{8}}26).
Решение:
Согласно вышеописанным правилам:
( displaystyle left. begin{array}{l}{{log }_{8}}26>{{log }_{8}}25\{{log }_{8}}25>{{log }_{9}}25={{log }_{3}}5text{ }end{array} right|Rightarrow text{ }{{log }_{8}}26>{{log }_{3}}5)
А теперь формула для продвинутых.
Правило сравнения логарифмов можно записать и короче:
( displaystyle {{log }_{a}}x-{{log }_{a}}yvee 0text{ }Leftrightarrow text{ }left( a-1 right)left( x-y right)vee 0)
Пример:
Что больше: ( displaystyle log _{0,3}^{2}sqrt{5}) или ( displaystyle log _{0,3}^{2}0,45)?
Решение:
( displaystyle begin{array}{l}log _{0,3}^{2}sqrt{5}vee log _{0,3}^{2}0,45text{ }Leftrightarrow text{ }log _{0,3}^{2}sqrt{5}-log _{0,3}^{2}0,45vee 0text{ }Leftrightarrow \left( {{log }_{0,3}}sqrt{5}-{{log }_{0,3}}0,45 right)left( {{log }_{0,3}}sqrt{5}+{{log }_{0,3}}0,45 right)vee 0text{ }Leftrightarrow \left( {{log }_{0,3}}sqrt{5}-{{log }_{0,3}}0,45 right)left( {{log }_{0,3}}sqrt{5}-{{log }_{0,3}}{{0,45}^{-1}} right)vee 0text{ }Leftrightarrow text{ }\underbrace{underbrace{left( 0,3-1 right)}_{<0}underbrace{left( sqrt{5}-0,45 right)}_{>0}underbrace{left( 0,3-1 right)}_{<0}}_{>0}left( sqrt{5}-frac{20}{9} right)vee 0text{ }Leftrightarrow \left( sqrt{5}-frac{20}{9} right)vee 0text{ }Leftrightarrow text{ }sqrt{5}vee frac{20}{9}text{ }Leftrightarrow text{ }5vee frac{400}{81}text{ }Leftrightarrow text{ }frac{400}{80}overset{>}{mathop{vee }},frac{400}{81}text{ }Rightarrow \Rightarrow text{ }underline{underline{log _{0,3}^{2}sqrt{5}>log _{0,3}^{2}0,45}}end{array})
Пример:
Сравните, какое из чисел больше: ( displaystyle log _{6}^{2}13text{ }vee text{ }2,25).
Решение:
( displaystyle begin{array}{l}log _{6}^{2}14vee 2,25text{ }Leftrightarrow text{ }log _{6}^{2}14-{{1,5}^{2}}vee 0text{ }Leftrightarrow text{ }\Leftrightarrow left( {{log }_{6}}14-{{log }_{6}}{{6}^{1,5}} right)underbrace{left( {{log }_{6}}14+{{log }_{6}}{{6}^{1,5}} right)}_{>0}vee 0text{ }Leftrightarrow \left( 6-1 right)left( 14-{{6}^{frac{3}{2}}} right)vee 0text{ }Leftrightarrow text{ }14vee sqrt{{{6}^{3}}}text{ }Leftrightarrow text{ }194overset{<}{mathop{vee }},216text{ }Rightarrow \Rightarrow text{ }underline{underline{log _{6}^{2}14<2,25}}end{array})
Сравнение тригонометрических выражений
Что такое синус, косинус, тангенс, котангенс? Для чего нужна единичная тригонометрическая окружность и как на ней найти значение тригонометрических функций?
Если ты не знаешь ответы на эти вопросы, очень рекомендую тебе прочитать теорию по этой теме. А если знаешь, то сравнить тригонометрические выражения между собой для тебя не составляет труда!
Немного освежим память.
Нарисуем единичную тригонометрическую окружность и вписанный в нее треугольник. Справился?
Теперь отметь, по какой стороне у нас откладывается косинус, а по какой синус, используя стороны треугольника. (ты, конечно помнишь, что синус, это отношение противолежащей стороны к гипотенузе, а косинус прилежащей?). Нарисовал? Отлично!
Последний штрих – проставь, где у нас будет ( 0{}^circ ) , где ( 90{}^circ )и так далее. Проставил? Фух)
Сравниваем, что получилось у меня и у тебя.
Фух! А теперь приступаем к сравнению!
Допустим, нам необходимо сравнить ( sin 30{}^circ ) и ( sin 60{}^circ ).
Нарисуй эти углы, используя подсказки в рамочках (где у нас отмечено ( sin 0{}^circ ), где ( sin 90{}^circ )), откладывая точки на единичной окружности.
Справился? Вот что у меня получилось.
Теперь опустим перпендикуляр из точек, отмеченных нами на окружности на ось… Какую? Какая ось у нас показывает значение синусов? Правильно, ( Oy).
Вот что у тебя должно получиться:
Глядя на этот рисунок, что больше: ( sin 30{}^circ ) или ( sin 60{}^circ )?
Конечно, ( sin 60{}^circ ), ведь точка ( F) находится выше точки ( E).
( sin 30{}^circ <sin 60{}^circ )
Аналогичным образом мы сравниваем значение косинусов. Только перпендикуляр мы опускаем на ось… Верно, ( Ox).
Соответственно, смотрим, какая точка находится правее (ну или выше, как в случае с синусами), то значение и больше.
Наверное, ты уже догадываешься, как сравнивать тангенсы, верно? Все, что нужно, знать что такое тангенс.
Так что такое тангенс? Правильно, отношение синуса к косинусу.
Чтобы сравнить тангенсы мы так же рисуем угол, как и в предыдущем случае. Допустим, нам необходимо сравнить:
( tg 30{}^circ vee tg 60{}^circ )
Нарисовал? Теперь так же отмечаем значения синуса на координатной оси ( Oy). Отметил?
А теперь укажи значения косинуса на координатной прямой ( Ox). Получилось? Давай сравним:
Как ты думаешь, что будет дальше?
Распишем по отрезкам, что такое ( tg {{30}^{{}^circ }}) и ( tg {{30}^{{}^circ }})
( tg {{30}^{{}^circ }}=frac{AE}{AG})
( tg {{60}^{{}^circ }}=frac{AF}{AH})
А теперь проанализируй написанное. ( tg {{60}^{{}^circ }}) — мы большой отрезок делим на маленький. В ответе будет значение, которое точно больше единицы. Верно?
А при ( tg {{30}^{{}^circ }}) мы маленький делим на большой. В ответе будет число, которое точно меньше единицы.
Так значение какого тригонометрического выражения больше?
Правильно:
( tg {{30}^{{}^circ }} < tg {{60}^{{}^circ }})
Как ты теперь понимаешь, сравнение котангенсов – то же самое, только наоборот: мы смотрим, как относятся друг к другу отрезки, определяющие косинус и синус.
