Как найти максимальное расстояние по графику

1. Нахождение пути по графику зависимости скорости от времени

Покажем, как можно найти пройденный телом путь с помощью графика зависимости скорости от времени.

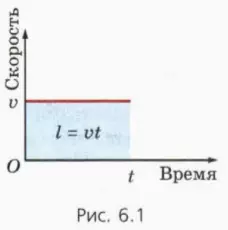
Начнем с самого простого случая – равномерного движения. На рисунке 6.1 изображен график зависимости v(t) – скорости от времени. Он представляет собой отрезок прямой, параллельной осн времени, так как при равномерном движении скорость постоянна.

Фигура, заключенная под этим графиком, – прямоугольник (он закрашен на рисунке). Его площадь численно равна произведению скорости v на время движения t. С другой стороны, произведение vt равно пути l, пройденному телом. Итак, при равномерном движении

путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени.

Покажем теперь, что этим замечательным свойством обладает и неравномерное движение.

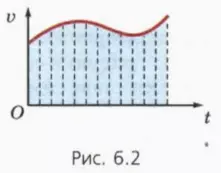
Пусть, например, график зависимости скорости от времени имеет вид кривой, изображенной на рисунке 6.2.

Разобьем мысленно все время движения на столь малые промежутки, чтобы в течение каждого из них движение тела можно было считать практически равномерным (это разбиение показано штриховыми линиями на рисунке 6.2).

Тогда путь, пройденный за каждый такой промежуток, численно равен площади фигуры под соответствующим ком графика. Поэтому и весь путь равен площади фигур заключенной под всем графиком. (Использованный нами прием лежит в основе интегрального исчисления, основы которого вы будете изучать в курсе «Начала математического анализа».)

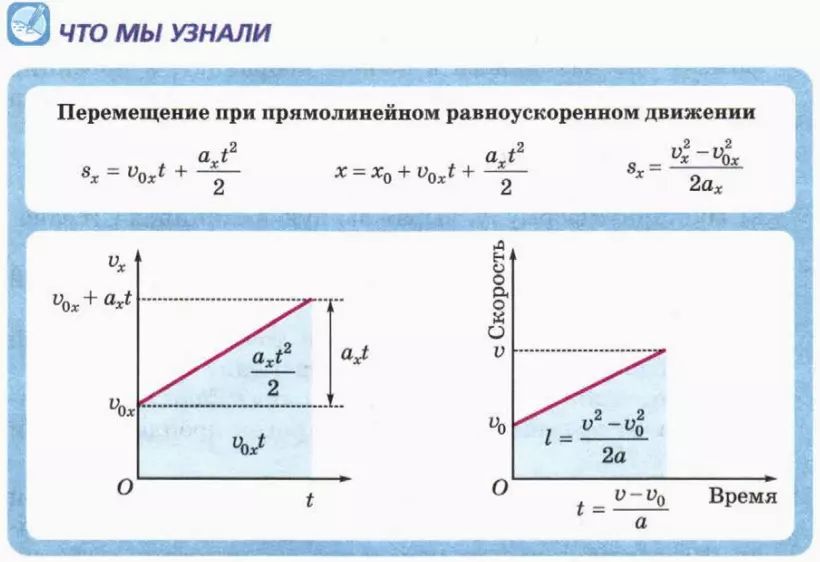
2. Путь и перемещение при прямолинейном равноускоренном движении

Применим теперь описанный выше способ нахождения пути к прямолинейному равноускоренному движению.

Начальная скорость тела равна нулю

Направим ось x в сторону ускорения тела. Тогда a_x = a, v_x = v. Следовательно,

v = at.     (1)

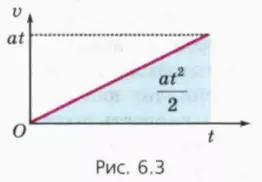
На рисунке 6.3 изображен график зависимости v(t).

? 1. Используя рисунок 6.3, докажите, что при прямолинейном равноускоренном движении без начальной скорости путь l выражается через модуль ускорения a и время движения t формулой

l = at²/2.     (2)

Главный вывод:

при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату времени движения.

Этим равноускоренное движение существенно отличается от равномерного.

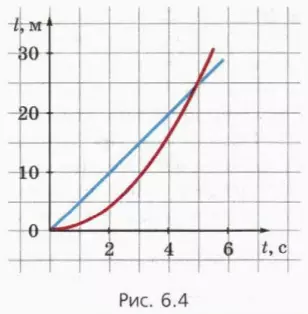
На рисунке 6.4 приведены графики зависимости пути от времени для двух тел, одно из которых движется равномерно, а другое – равноускоренно без начальной скорости.

? 2. Рассмотрите рисунок 6.4 и ответьте на вопросы.
а) Каким цветом изображен график для тела, движущегося равноускоренно?
б) Чему равно ускорение этого тела?
в) Чему равны скорости тел в тот момент, когда они прошли одинаковый путь?
г) В какой момент времени скорости тел равны?

? 3. Тронувшись с места, автомобиль за первые 4 с проехал расстояние 20 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какое расстояние проедет автомобиль:
а) за 8 с? б) за 16 с? в) за 2 с?

Найдем теперь зависимость проекции перемещения s_x от времени. В данном случае проекция ускорения на ось x положительна, поэтому s_x = l, a_x = a. Таким образом, из формулы (2) следует:

s_x = a_xt²/2.     (3)

Формулы (2) и (3) очень похожи, что приводит порой к ошибкам при решении простых задач. Дело в том, что значение проекции перемещения может быть отрицательным. Так будет, если ось x направлена противоположно перемещению: тогда s_x < 0. А путь отрицательным быть не может!

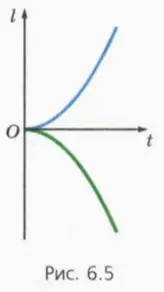
? 4. На рисунке 6.5 изображены графики зависимости от времени пути и проекции перемещения для некоторого тела. Какой цвет у графика проекции перемещения?

Начальная скорость тела не равна нулю

Напомним, что в таком случае зависимость проекции скорости от времени выражается формулой

v_x = v_0x + a_xt,     (4)

где v_0x – проекция начальной скорости на ось x.

Мы рассмотрим далее случай, когда v_0x > 0, a_x > 0. В этом случае снова можно воспользоваться тем, что путь численно равен площади фигуры под графиком зависимости скорости от времени. (Другие комбинации знаков проекции начальной скорости и ускорения рассмотрите самостоятельно: в результате получится та же общая формула (5).

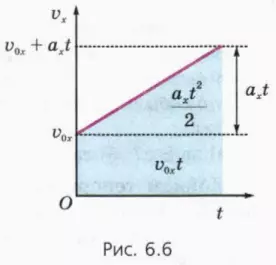
На рисунке 6.6 изображен график зависимости v_x(t) при v_0x > 0, a_x > 0.

? 5. Используя рисунок 6.6, докажите, что при прямолинейном равноускоренном движении с начальной скоростью проекция перемещения

s_x = v_0x + a_xt²/2.     (5)

Эта формула позволяет найти зависимость координаты x тела от времени. Напомним (см. формулу (6), § 2), что координата x тела связана с проекцией его перемещения s_x соотношением

s_x = x – x₀,

где x₀ — начальная координата тела. Следовательно,

x = x₀ + s_x,     (6)

Из формул (5), (6) получаем:

x = x₀ + v_0xt + a_xt²/2.     (7)

6. Зависимость координаты от времени для некоторого тела, движущегося вдоль оси x, выражается в единицах СИ формулой x = 6 – 5t + t².
а) Чему равна начальная координата тела?
б) Чему равна проекция начальной скорости на ось x?
в) Чему равна проекция ускорения на ось x?
г) Начертите график зависимости координаты x от времени.
д) Начертите график зависимости проекции скорости от времени.
е) В какой момент скорость тела равна нулю?
ж) Вернется ли тело в начальную точку? Если да, то в какой момент (моменты) времени?
з) Пройдет ли тело через начало координат? Если да, то в какой момент (моменты) времени?
и) Начертите график зависимости проекции перемещения от времени.
к) Начертите график зависимости пути от времени.

3. Соотношение между путем и скоростью

При решении задач часто используют соотношения между путем, ускорением и скоростью (начальной v₀, конечной v или ими обеими). Выведем эти соотношения. Начнем с движения без начальной скорости. Из формулы (1) получаем для времени движения:

t = v/a.      (8)

Подставим это выражение в формулу (2) для пути:

l = at²/2 = a/2(v/a)² = v²/2a.     (9)

Главный вывод:

при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату конечной скорости.

? 7. Тронувшись с места, автомобиль набрал скорость 10 м/с на пути 40 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какой путь от начала движения проехал автомобиль, когда его скорость была равна: а) 20 м/с? б) 40 м/с? в) 5 м/с?

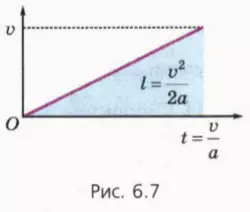
Соотношение (9) можно получить также, вспомнив, что путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени (рис. 6.7).

Это соображение поможет вам легко справиться со следующим заданием.

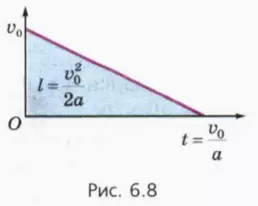
? 8. Используя рисунок 6.8, докажите, что при торможении с постоянным ускорением тело проходит до полной остановки путь l_т = v₀²/2a, где v₀ – начальная скорость тела, a – модуль ускорения.

В случае торможения транспортного средства (автомобиль, поезд) путь, пройденный до полной остановки, называют тормозным путём. Обратите внимание: тормозной путь при начальной скорости v₀ и путь, пройденный при разгоне с места до скорости v₀ с тем же по модулю ускорением a, одинаковы.

? 9. При экстренном торможении на сухом асфальте ускорение автомобиля равно по модулю 5 м/с². Чему равен тормозной путь автомобиля при начальной скорости: а) 60 км/ч (максимальная разрешенная скорость в городе); б) 120 км/ч? Найдите тормозной путь при указанных скоростях во время гололеда, когда модуль ускорения равен 2 м/с². Сравните найденные вами значения тормозного пути с длиной классной комнаты.

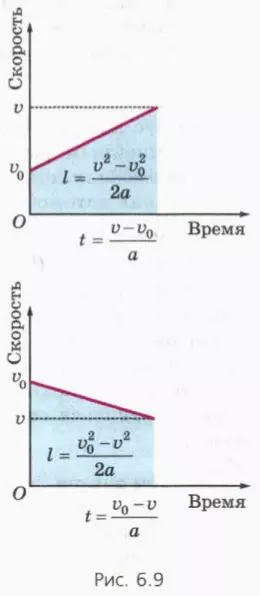
? 10. Используя рисунок 6.9 и формулу, выражающую площадь трапеции через ее высоту и полусумму оснований, докажите, что при прямолинейном равноускоренном движении:
а) l = (v² – v₀²)/2a, если скорость тела увеличивается;
б) l = (v₀² – v²)/2a, если скорость тела уменьшается.

? 11. Докажите, что проекции перемещения, начальной и конечной скорости, а также ускорения связаны соотношением

s_x = (v_x² – v_0x²)/2ax     (10)

? 12. Автомобиль на пути 200 м разогнался от скорости 10 м/с до 30 м/с.
а) С каким ускорением двигался автомобиль?
б) За какое время автомобиль проехал указанный путь?
в) Чему равна средняя скорость автомобиля?

Лютый опыт

Дополнительные вопросы и задания

13. От движущегося поезда отцепляют последний вагон, после чего поезд движется равномерно, а вагон – с постоянным ускорением до полной остановки.
а) Изобразите на одном чертеже графики зависимости скорости от времени для поезда и вагона.
б) Во сколько раз путь, пройденный вагоном до остановки, меньше пути, пройденного поездом за то же время?

14. Отойдя от станции, электричка какое-то время ехала равноускоренно, затем в течение 1 мин – равномерно со скоростью 60 км/ч, после чего снова равноускоренно до остановки на следующей станции. Модули ускорений при разгоне и торможении были различны. Расстояние между станциями электричка прошла за 2 мин.
а) Начертите схематически график зависимости проекции скорости электрички от времени.
б) Используя этот график, найдите расстояние между станциями.
в) Какое расстояние проехала бы электричка, если бы на первом участке пути она разгонялась, а на втором – тормозила? Какова была бы при этом ее максимальная скорость?

15. Тело движется равноускоренно вдоль оси x. В начальный момент оно находилось в начале координат, а проекция его скорости была равна 8 м/с. Через 2 с координата тела стала равной 12 м.
а) Чему равна проекция ускорения тела?
б) Постройте график зависимости v_x(t).
в) Напишите формулу, выражающую в единицах СИ зависимость x(t).
г) Будет ли скорость тела равна нулю? Если да, то в какой момент времени?
д) Побывает ли тело второй раз в точке с координатой 12 м? Если да, то в какой момент времени?
е) Вернется ли тело в начальную точку? Если да, то в какой момент времени, и чему будет равен пройденный при этом путь?

16. После толчка шарик вкатывается вверх по наклонной плоскости, после чего возвращается в начальную точку. На расстоянии b от начальной точки шарик побывал дважды через промежутки времени t₁ и t₂ после толчка. Вверх и вниз вдоль наклонной плоскости шарик двигался с одинаковым по модулю ускорением.
а) Направьте ось x вверх вдоль наклонной плоскости, выберите начало координат в точке начального положения шарика и напишите формулу, выражающую зависимость x(t), в которую входят модуль начальной скорости шарика v0 и модуль ускорения шарика a.
б) Используя эту формулу и тот факт, что на расстоянии b от начальной точки шарик побывал в моменты времени t₁ и t₂ составьте систему двух уравнений с двумя неизвестными v₀ и a.
в) Решив эту систему уравнений, выразите v₀ и a через b, t₁ и t₂.
г) Выразите весь пройденный шариком путь l через b, t₁ и t₂.
д) Найдите числовые значения v₀, a и l при b = 30 см, t₁ = 1с, t₂ = 2 с.
е) Постройте графики зависимости v_x(t), s_x(t), l(t).
ж) С помощью графика зависимости sx(t) определите момент, когда модуль перемещения шарика был максимальным.

public void MaxSpacing(object chart, int series1, int series2) 
{
    Chart tmpChart = (Chart)chart;
    double distance = 0;
    int positon = 0;
    for (int i = 0; i < tmpChart.Series[series1].Points.Count(); i++)
    {
        if ((Math.Abs(tmpChart.Series[series1].Points[i].YValues[0] - tmpChart.Series[series2].Points[i].YValues[0])) > distance)
        {
            distance = tmpChart.Series[series1].Points[i].YValues[0] - tmpChart.Series[series2].Points[i].YValues[0];
        }
}

2 ответа

Лучший ответ

double distance = 0;
Series series1 = tmpChart.Series[series1];
Series series2 = tmpChart.Series[series2];
Series seriesToEnumerate = series1.Points.Count() >= series2.Points.Count() ? series1 : series2;

for (int i = 0; i < series1.Count(); ++i)
{
    DataPoint point1 = series1.Points[i];
    DataPoint point2 = series2.Points[i];

    if (point1.X == point2.X)
    {
        distance = Math.Abs(point1.Y - point2.Y) // if greater than previous distance
    }
    else
    {
        // find two points in series2 whose X values surround point1.X, call them point3 and point4

        // Interpolate between point3 and point4 to find the y value at the x of point1
        double slope = (point4.Y - point3.Y) / (point4.X - point3.X);
        double intercept = point4.Y - slope * point4.X;
        double y2 = slope * point1.X + intercept;

        distance = Math.Abs(point1.Y - y2); // if this is greater than previous distance
    }
}

public void MaxSpacing(object chart, int series1, int series2)
{
    Chart tmpChart = (Chart)chart;
    double distance = 0;
    int position = 0;
    for (int i = 0; i < tmpChart.Series[series1].Points.Count(); i++) {
        if ((Math.Abs(tmpChart.Series[series1].Points[i].YValues[0] - tmpChart.Series[series2].Points[i].YValues[0])) > distance) {
            distance = tmpChart.Series[series1].Points[i].YValues[0] - tmpChart.Series[series2].Points[i].YValues[0];
        }
    }

    int len1 = tmpChart.Series[series1].Points.Count(), len2 = tmpChart.Series[series2].Points.Count();
    for (int i1 = 0, i2 = 0; i1 < len1 && i2 < len2;) {
        var x1 = tmpChart.Series[series1].Points[i1].XValue;
        var x2 = tmpChart.Series[series2].Points[i2].XValue;
        if (x1 < x2) {
            i1++;
        } else if (x2 < x1) {
            i2++;
        } else {
            double d = Math.Abs(tmpChart.Series[series1].Points[i1].YValues[0] - tmpChart.Series[series2].Points[i2].YValues[0]);
            if (d > distance) {
                distance = d;
                position = i1; //I'm guessing here
            }
            i1++;
            i2++;
        }
    }

}

Ответ или решение 2

Скорость движения рассчитывается по формуле

• Скорость движения равна производной формулы пути;
• чтобы найти максимальную скорость, нужно найти производную скорости;
• затем нужно определить точки максимума;
• подставить их в уравнение скорости.

Нам дано уравнение пути s = -10t 3 + 15t 2 + 2t

Найдем уравнение скорости

S` = — 10 * 3t 2 + 15 * 2t + 2 = — 30t 2 + 30t + 2

v = — 30t 2 + 30t + 2

Найдем точки максимума этой функции

Для этого найдем производную этой функции.

v`= — 30 * 2t + 30 = — 60t + 30

Приравняем ее к нулю.

Переносим 30 в правую часть, меняя знак.

Делим все уравнение на (- 30).

Чтобы узнать знак производной, рисуем координатную прямую, отмечаем точку 1/2 и определяем знаки производной подбором.

Берем любую точку, например, 0.

— 60 * 0 + 30 = 30 (производная положительна, функция возрастает)

Берем например, точку 1.

— 60 * 1 + 30 = — 30 (производная отрицательна, функция убывает)

Значит, t = 1/2 — это точка максимума.

Подставим это значение в уравнение скорости.

v = — 30t 2 + 30t + 2

v = — 30(1/2) 2 + 30 * 1/2 + 2 = — 7,5 + 15 + 2 = 9,5.

Ответ: максимальная скорость движения равна 9,5.

Из уравнения S = — 10t^3 + 15t^2 + 2t сначала найдем производную пути по времени(это будет уравнение скорости точки): S'(t) = V(t) = — 30t^2 + 30t + 2. Графиком функции данного уравнения является парабола и как видим около t^2(то есть коэффициент а) стоит отрицательное число, значит ветки параболы направлены вниз и максимальное значение t достигается на вершине параболы, найдем ее: tmax = — b / 2a = 30 / 30 * 2 = 0,5. Подставим в уравнение скорости и найдем Vmax получим Vmax = — 30 * 0,5^2 + 30 * 0,5 + 2 = 9,5.

• Попроси больше объяснений
• Следить
• Отметить нарушение

Vazgen1312 05.07.2019

Ответ

Ответ:

Объяснение:

Находим L. Разделим путь на три отрезка(как на графике)(с 0 по 1 секунду, потом с 1 до 4 секунды и с 4 по 5 секунду)

1. S = Vot(начальная скорость умноженная на время) + at²/2 ; a(ускорение) = ΔV/Δt = 15 м/с²

S = 0 + 15*1/2 = 7,5 м

2. S = V*t = 15*3 = 45 м

3. S = Vot + at²/2 ; a = ΔV/Δt = — 15 м/с² (тело тормозит)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

То есть ускорение – это величина, которая определяется изменением скорости за время, в течение которого это изменение произошло.

Еще раз о том, что такое равноускоренное движение

Автомобиль за каждую секунду увеличивает свою скорость на . Движется ли автомобиль равноускоренно?

На первый взгляд, кажется, да, ведь за равные промежутки времени скорость увеличивается на равные величины. Давайте рассмотрим подробнее движение на протяжении 1 с. Возможен такой случай, что первые 0,5 с автомобиль двигался равномерно и увеличил свою скорость на Часто равноускоренным называют такое движение, при котором тело двигается с постоянным ускорением . Самым простым примером равноускоренного движения является свободное падение тела (тело падает под действием силы тяжести).

Уравнение скорости

Воспользовавшись уравнением, определяющим ускорение , удобно записать формулу для вычисления мгновенной скорости любого промежутка и для любого момента времени:

Уравнение скорости в проекциях имеет вид:

Это уравнение дает возможность определить скорость в любой момент движения тела. При работе с законом изменения скорости от времени необходимо учитывать направление скорости по отношению к выбранной СО.

К вопросу о направлении скорости и ускорения

В равномерном движении направление скорости и перемещения всегда совпадают. В случае равноускоренного движения направление скорости не всегда совпадает с направлением ускорения и не всегда направление ускорения указывает направление движения тела.

Рассмотрим наиболее типичные примеры направления скорости и ускорения.

1. Скорость и ускорение направлены в одну сторону вдоль одной прямой (рис. 1).

Рис. 1. Скорость и ускорение направлены в одну сторону вдоль одной прямой

В данном случае тело разгоняется. Примерами такого движения могут быть свободное падение, начало движения и разгон автобуса, старт и разгон ракеты.

2. Скорость и ускорение направлены в разные стороны вдоль одной прямой (рис. 2).

Рис. 2. Скорость и ускорение направлены в разные стороны вдоль одной прямой

Такое движение иногда называют равнозамедленным. В таком случае говорят, что тело тормозит. В конечном итоге оно либо остановится, либо начнет двигаться в противоположном направлении. Пример такого движения – камень, подброшенный вертикально вверх.

3. Скорость и ускорение взаимно перпендикулярны (рис. 3).

Рис. 3. Скорость и ускорение взаимно перпендикулярны

Примерами такого движения является движение Земли вокруг Солнца и движение Луны вокруг Земли. В этом случаи траекторией движения будет окружность.

Таким образом, направление ускорения не всегда совпадает с направлением скорости, но всегда совпадает с направлением изменения скорости.

График скорости

График скорости (проекции скорости) представляет собой закон изменения скорости (проекции скорости) от времени для равноускоренного прямолинейного движения, представленный графически.

Рис. 4. Графики зависимости проекции скорости от времени для равноускоренного прямолинейного движения

Проанализируем различные графики.

Первый. Уравнение проекции скорости:

Второй – это зависимость при отрицательном значении проекции ускорения, когда движение замедленно, то есть скорость по модулю сначала уменьшается. В этом случае уравнение выглядит так:

График начинается в точке

Где

Рис. 5. График функции

Это уравнение прямой, что подтверждается графиками, рассмотренными нами.

Некоторые частные случаи

Чтобы окончательно разобраться с графиком скорости, рассмотрим частные случаи. На первом графике зависимость скорости от времени связана с тем, что начальная скорость, , равняется нулю, проекция ускорения больше нуля.

Запись этого уравнения . А сам вид графика достаточно простой (график 1).

Рис. 6. Различные случаи равноускоренного движения

Еще два случая равноускоренного движения представлены на следующих двух графиках. Второй случай – это ситуация, когда сначала тело двигалось с отрицательной проекцией ускорения, а затем начало разгоняться в положительном направлении оси.

Третий случай – это ситуация, когда проекция ускорения меньше нуля и тело непрерывно движется в направлении, противоположном положительному направлению оси . При этом модуль скорости постоянно возрастает, тело ускоряется.

График зависимости ускорения от времени

Равноускоренное движение – это движение, при котором ускорение тела не меняется.

Рис. 7. График зависимости проекций ускорения от времени

Если какая-либо зависимость является постоянной, то на графике она изображается прямой, параллельной оси абсцисс. Прямые I и II – прямые движения для двух разных тел. Обратите внимание, что прямая I лежит выше прямой абсцисс (проекция ускорения положительна), а прямая II – ниже (проекция ускорения отрицательна). Если бы движение было равномерным, то проекция ускорения совпала бы с осью абсцисс.

Рассмотрим рис. 8. Площадь фигуры, ограниченной осями, графиком и перпендикуляром к оси абсцисс, равна:

Произведение ускорения и времени –это изменение скорости за данное время.

Рис. 8. Изменение скорости

Площадь фигуры, ограниченной осями, зависимостью и перпендикуляром к оси абсцисс, численно равна изменению скорости тела.

Мы использовали слово «численно», поскольку единицы измерения площади и изменения скорости не совпадают.

Заключение

На данном уроке мы познакомились с уравнением скорости и научились графически изображать данное уравнение.

1. Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. – М.: «Просвещение».
2. Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
3. Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «class-fizika.narod.ru» (Источник)
2. Интернет-портал «youtube.com» (Источник)
3. Интернет-портал «fizmat.by» (Источник)
4. Интернет-портал «sverh-zadacha.ucoz.ru» (Источник)

1. Что такое равноускоренное движение?

2. Охарактеризуйте движение тела и определите пройденный путь тела по графику за 2 с от начала движения:

3. На каком из графиков изображена зависимость проекции скорости тела от времени при равноускоренном движении при ?

«>