Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 июля 2021 года; проверки требуют 7 правок.
Мультипликативная группа кольца вычетов по модулю m — мультипликативная группа обратимых элементов кольца вычетов по модулю m. При этом в качестве множества элементов может рассматриваться любая приведенная система вычетов по модулю m.
Приведённая система вычетов[править | править код]
Приведённая система вычетов по модулю m — множество всех чисел полной системы вычетов по модулю m, взаимно простых с m.
В качестве приведённой системы вычетов по модулю m обычно берутся взаимно простые с m числа от 1 до m — 1[1].
Пример: приведенной системой вычетов по модулю 42 будет: { 1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41 }.
- Свойства
- Набор любых
(функция Эйлера) попарно несравнимых по модулю m и взаимно простых с m чисел образует приведённую систему вычетов по модулю
[1].
- Если НОД(a,m) = 1, то множество значений ax, где x пробегает приведенную систему вычетов по модулю m, также является приведенной системой вычетов по модулю m[2].
- Если НОД(k,m) = 1, то множество значений kx + my, где x пробегает приведенную систему вычетов по модулю m и y пробегает приведенную систему вычетов по модулю k, является приведенной системой вычетов по модулю km[3].
- В случае, когда число m простое, приведенная система вычетов по модулю m отличается от полной системы вычетов отсутствием нуля[4].
- Если a — элемент приведенной системы вычетов по модулю m, то, для любого b сравнение
разрешимо относительно x[4].
Приведённая система вычетов с умножением по модулю m образует группу, называемую мультипликативной группой или мультипликативной группой обратимых элементов кольца вычетов по модулю m, которая обозначается 

Если m простое, то, как отмечалось выше, элементы 1, 2, …,m-1 входят в 

Формы записи[править | править код]
Кольцо вычетов по модулю n обозначают 







Простейший случай[править | править код]
Чтобы понять структуру группы 




Теорема: 
Пример: Рассмотрим группу 
-
-
= {1,2,4,5,7,8}
- Генератором группы является число 2.
- Как видим, любой элемент группы
может быть представлен в виде
, где
. То есть группа
— циклическая.
-
Общий случай[править | править код]
Для рассмотрения общего случая необходимо определение примитивного корня.
Примитивный корень по простому модулю 

- Примеры: 2 — примитивный корень по модулю 11; 8 — примитивный корень по модулю 11; 3 не является примитивным корнем по модулю 11.
В случае целого модуля 
Структуру группы определяет следующая теорема: Если p — нечётное простое число и 


Из китайской теоремы об остатках следует, что при 


Группа 

Группа 



Группа 




Подгруппа свидетелей простоты[править | править код]
Пусть 






или
Если число 



Пример: 













Свойства[править | править код]
Экспонента группы[править | править код]
Экспонента группы равна функции Кармайкла 
Порядок группы[править | править код]
Порядок группы равен функции Эйлера: 




Порождающее множество[править | править код]


Пример[править | править код]
Приведённая система вычетов по модулю 

![[1]_{{10}},[3]_{{10}},[7]_{{10}},[9]_{{10}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e66cdbdd2d19559aa6abc3293393d5339c645a3f)
Относительно определённого для классов вычетов умножения они образуют группу, причём ![[3]_{{10}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8247394a3bbfaa0f8ab29bd0f800e2e341ea2e60)
![[7]_{{10}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a00fe680b0c3c4a5b1af33652e1a4203f112e2cb)
![[3]_{{10}}{cdot }[7]_{{10}}=[1]_{{10}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93d0d877e625d6cfa43c6c518854c560dac31ac7)
а ![[1]_{{10}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ec7f57520554876b866e6f28e531ff29f48aedd)
![[9]_{{10}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3966de95f6e2096a6c9a7c25ecf568bc30099cb)
Структура группы[править | править код]
Запись 
 |
 |
 |
 |
Генератор группы |  |
 |
 |
 |
Генератор группы |  |
 |
 |
 |
Генератор группы |  |
 |
 |
 |
Генератор группы | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | C1 | 1 | 1 | 0 | 33 | C2×C10 | 20 | 10 | 2, 10 | 65 | C4×C12 | 48 | 12 | 2, 12 | 97 | C96 | 96 | 96 | 5 | |||
| 2 | C1 | 1 | 1 | 1 | 34 | C16 | 16 | 16 | 3 | 66 | C2×C10 | 20 | 10 | 5, 7 | 98 | C42 | 42 | 42 | 3 | |||
| 3 | C2 | 2 | 2 | 2 | 35 | C2×C12 | 24 | 12 | 2, 6 | 67 | C66 | 66 | 66 | 2 | 99 | C2×C30 | 60 | 30 | 2, 5 | |||
| 4 | C2 | 2 | 2 | 3 | 36 | C2×C6 | 12 | 6 | 5, 19 | 68 | C2×C16 | 32 | 16 | 3, 67 | 100 | C2×C20 | 40 | 20 | 3, 99 | |||
| 5 | C4 | 4 | 4 | 2 | 37 | C36 | 36 | 36 | 2 | 69 | C2×C22 | 44 | 22 | 2, 68 | 101 | C100 | 100 | 100 | 2 | |||
| 6 | C2 | 2 | 2 | 5 | 38 | C18 | 18 | 18 | 3 | 70 | C2×C12 | 24 | 12 | 3, 69 | 102 | C2×C16 | 32 | 16 | 5, 101 | |||
| 7 | C6 | 6 | 6 | 3 | 39 | C2×C12 | 24 | 12 | 2, 38 | 71 | C70 | 70 | 70 | 7 | 103 | C102 | 102 | 102 | 5 | |||
| 8 | C2×C2 | 4 | 2 | 3, 5 | 40 | C2×C2×C4 | 16 | 4 | 3, 11, 39 | 72 | C2×C2×C6 | 24 | 6 | 5, 17, 19 | 104 | C2×C2×C12 | 48 | 12 | 3, 5, 103 | |||
| 9 | C6 | 6 | 6 | 2 | 41 | C40 | 40 | 40 | 6 | 73 | C72 | 72 | 72 | 5 | 105 | C2×C2×C12 | 48 | 12 | 2, 29, 41 | |||
| 10 | C4 | 4 | 4 | 3 | 42 | C2×C6 | 12 | 6 | 5, 13 | 74 | C36 | 36 | 36 | 5 | 106 | C52 | 52 | 52 | 3 | |||
| 11 | C10 | 10 | 10 | 2 | 43 | C42 | 42 | 42 | 3 | 75 | C2×C20 | 40 | 20 | 2, 74 | 107 | C106 | 106 | 106 | 2 | |||
| 12 | C2×C2 | 4 | 2 | 5, 7 | 44 | C2×C10 | 20 | 10 | 3, 43 | 76 | C2×C18 | 36 | 18 | 3, 37 | 108 | C2×C18 | 36 | 18 | 5, 107 | |||
| 13 | C12 | 12 | 12 | 2 | 45 | C2×C12 | 24 | 12 | 2, 44 | 77 | C2×C30 | 60 | 30 | 2, 76 | 109 | C108 | 108 | 108 | 6 | |||
| 14 | C6 | 6 | 6 | 3 | 46 | C22 | 22 | 22 | 5 | 78 | C2×C12 | 24 | 12 | 5, 7 | 110 | C2×C20 | 40 | 20 | 3, 109 | |||
| 15 | C2×C4 | 8 | 4 | 2, 14 | 47 | C46 | 46 | 46 | 5 | 79 | C78 | 78 | 78 | 3 | 111 | C2×C36 | 72 | 36 | 2, 110 | |||
| 16 | C2×C4 | 8 | 4 | 3, 15 | 48 | C2×C2×C4 | 16 | 4 | 5, 7, 47 | 80 | C2×C4×C4 | 32 | 4 | 3, 7, 79 | 112 | C2×C2×C12 | 48 | 12 | 3, 5, 111 | |||
| 17 | C16 | 16 | 16 | 3 | 49 | C42 | 42 | 42 | 3 | 81 | C54 | 54 | 54 | 2 | 113 | C112 | 112 | 112 | 3 | |||
| 18 | C6 | 6 | 6 | 5 | 50 | C20 | 20 | 20 | 3 | 82 | C40 | 40 | 40 | 7 | 114 | C2×C18 | 36 | 18 | 5, 37 | |||
| 19 | C18 | 18 | 18 | 2 | 51 | C2×C16 | 32 | 16 | 5, 50 | 83 | C82 | 82 | 82 | 2 | 115 | C2×C44 | 88 | 44 | 2, 114 | |||
| 20 | C2×C4 | 8 | 4 | 3, 19 | 52 | C2×C12 | 24 | 12 | 7, 51 | 84 | C2×C2×C6 | 24 | 6 | 5, 11, 13 | 116 | C2×C28 | 56 | 28 | 3, 115 | |||
| 21 | C2×C6 | 12 | 6 | 2, 20 | 53 | C52 | 52 | 52 | 2 | 85 | C4×C16 | 64 | 16 | 2, 3 | 117 | C6×C12 | 72 | 12 | 2, 17 | |||
| 22 | C10 | 10 | 10 | 7 | 54 | C18 | 18 | 18 | 5 | 86 | C42 | 42 | 42 | 3 | 118 | C58 | 58 | 58 | 11 | |||
| 23 | C22 | 22 | 22 | 5 | 55 | C2×C20 | 40 | 20 | 2, 21 | 87 | C2×C28 | 56 | 28 | 2, 86 | 119 | C2×C48 | 96 | 48 | 3, 118 | |||
| 24 | C2×C2×C2 | 8 | 2 | 5, 7, 13 | 56 | C2×C2×C6 | 24 | 6 | 3, 13, 29 | 88 | C2×C2×C10 | 40 | 10 | 3, 5, 7 | 120 | C2×C2×C2×C4 | 32 | 4 | 7, 11, 19, 29 | |||
| 25 | C20 | 20 | 20 | 2 | 57 | C2×C18 | 36 | 18 | 2, 20 | 89 | C88 | 88 | 88 | 3 | 121 | C110 | 110 | 110 | 2 | |||
| 26 | C12 | 12 | 12 | 7 | 58 | C28 | 28 | 28 | 3 | 90 | C2×C12 | 24 | 12 | 7, 11 | 122 | C60 | 60 | 60 | 7 | |||
| 27 | C18 | 18 | 18 | 2 | 59 | C58 | 58 | 58 | 2 | 91 | C6×C12 | 72 | 12 | 2, 3 | 123 | C2×C40 | 80 | 40 | 7, 83 | |||
| 28 | C2×C6 | 12 | 6 | 3, 13 | 60 | C2×C2×C4 | 16 | 4 | 7, 11, 19 | 92 | C2×C22 | 44 | 22 | 3, 91 | 124 | C2×C30 | 60 | 30 | 3, 61 | |||
| 29 | C28 | 28 | 28 | 2 | 61 | C60 | 60 | 60 | 2 | 93 | C2×C30 | 60 | 30 | 11, 61 | 125 | C100 | 100 | 100 | 2 | |||
| 30 | C2×C4 | 8 | 4 | 7, 11 | 62 | C30 | 30 | 30 | 3 | 94 | C46 | 46 | 46 | 5 | 126 | C6×C6 | 36 | 6 | 5, 13 | |||
| 31 | C30 | 30 | 30 | 3 | 63 | C6×C6 | 36 | 6 | 2, 5 | 95 | C2×C36 | 72 | 36 | 2, 94 | 127 | C126 | 126 | 126 | 3 | |||
| 32 | C2×C8 | 16 | 8 | 3, 31 | 64 | C2×C16 | 32 | 16 | 3, 63 | 96 | C2×C2×C8 | 32 | 8 | 5, 17, 31 | 128 | C2×C32 | 64 | 32 | 3, 127 |
Применение[править | править код]
На сложности дискретного логарифмирования в мультипликативной группе кольца вычетов основана криптографическая стойкость шифрсистемы Эль-Гамаля.[7]
История[править | править код]
Вклад в исследование структуры мультипликативной группы кольца вычетов внесли Артин, Билхарц, Брауэр, Вильсон, Гаусс, Лагранж, Лемер, Варинг, Ферма, Хули, Эйлер.
Лагранж доказал лемму о том, что если ![f(x)in k[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/00b8295885af09a1a70a9008da19b502616b66e4)


Примечания[править | править код]
- ↑ 1 2 И. М. Виноградов Основы теории чисел. изд. 9-е, перераб., М. : Наука. 1981
- ↑ Сагалович Ю. Л. Введение в алгебраические коды. 2011.
- ↑ Бухштаб, 1966.
- ↑ 1 2 3 4 В. Босс Лекции по математике. Том 14. Теория чисел. 2014.
- ↑ 1 2 3 4 5 Айерлэнд, Роузен, 1987.
- ↑ Erdős, Paul; Pomerance, Carl. On the number of false witnesses for a composite number (англ.) // Math. Comput.[en] : journal. — 1986. — Vol. 46. — P. 259—279.
- ↑ Алферов и др., 2002.
Литература[править | править код]
- Айерлэнд К., Роузен М. Классическое введение в современную теорию чисел. — М.: Мир, 1987.
- Алферов А.П., Зубов А.Ю., Кузьмин А.С. Черемушкин А.В. Основы криптографии. — Москва: «Гелиос АРВ», 2002.
- Ростовцев А.Г., Маховенко Е.Б. Теоретическая криптография. — Санкт-Петербург: НПО «Профессионал», 2004.
Ссылки[править | править код]
- Бухштаб А. А. Теория чисел. — М.: Просвещение, 1966.
- Weisstein, Eric W. Modulo Multiplication Group (англ.) на сайте Wolfram MathWorld.
Мультипликативная группа кольца вычетов по модулю m — мультипликативная группа обратимых элементов кольца вычетов по модулю m. При этом в качестве множества элементов может рассматриваться любая приведенная система вычетов по модулю m.
Приведённая система вычетов
Приведённая система вычетов по модулю m — множество всех чисел полной системы вычетов по модулю m, взаимно простых с m.
В качестве приведённой системы вычетов по модулю m обычно берутся взаимно простые с m числа от 1 до m — 1[1].
Пример: приведенной системой вычетов по модулю 42 будет: { 1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41 }.
- Свойства
- Набор любых φ(m) (φ(m) — функция Эйлера) чисел, взаимно простых с m и несравнимых попарно по модулю m, образуют приведённую систему вычетов[1].
- Если НОД(a,m) = 1, то множество значений ax, где x пробегает приведенную систему вычетов по модулю m, также является приведенной системой вычетов по модулю m[2].
- Если НОД(k,m) = 1, то множество значений kx + my, где x пробегает приведенную систему вычетов по модулю m и y пробегает приведенную систему вычетов по модулю k, является приведенной системой вычетов по модулю km[3].
- В случае, когда число m простое, приведенная система вычетов по модулю m отличается от полной системы вычетов отсутствием нуля[4].
- Если a — элемент приведенной системы вычетов по модулю m, то, для любого b сравнение [math]displaystyle{ ax equiv b pmod{m} }[/math] разрешимо относительно x[4].
Приведённая система вычетов с умножением по модулю m образует группу, называемую мультипликативной группой или группой обратимых элементов кольца вычетов по модулю m, которая обозначается [math]displaystyle{ mathbb{Z}_m^{times} }[/math] или [math]displaystyle{ U(mathbb{Z}_m) }[/math][4].
Если m простое, то, как отмечалось выше, элементы 1, 2, …,m-1 входят в [math]displaystyle{ mathbb{Z}_m^{times} }[/math]. В этом случае [math]displaystyle{ mathbb{Z}_m^{times} }[/math] является полем[4].
Формы записи
Кольцо вычетов по модулю n обозначают [math]displaystyle{ mathbb{Z}/nmathbb{Z} }[/math] или [math]displaystyle{ mathbb{Z}_n }[/math]. Его мультипликативную группу, как и в общем случае групп обратимых элементов колец, обозначают [math]displaystyle{ (mathbb{Z}/nmathbb{Z})^*, }[/math] [math]displaystyle{ (mathbb{Z}/nmathbb{Z})^times, }[/math] [math]displaystyle{ U(mathbb{Z}/nmathbb{Z}), }[/math] [math]displaystyle{ E(mathbb{Z}/nmathbb{Z}), }[/math] [math]displaystyle{ mathbb{Z}_n^{times}, }[/math] [math]displaystyle{ U(mathbb{Z}_n) }[/math].
Простейший случай
Чтобы понять структуру группы [math]displaystyle{ U(mathbb{Z}/nmathbb{Z}) }[/math], можно рассмотреть частный случай
[math]displaystyle{ n=p^a }[/math], где [math]displaystyle{ p }[/math] — простое число, и обобщить его. Рассмотрим простейший случай, когда
[math]displaystyle{ a=1 }[/math], то есть [math]displaystyle{ n=p }[/math].
Теорема: [math]displaystyle{ U(mathbb{Z}/pmathbb{Z}) }[/math] — циклическая группа. [5]
Пример: Рассмотрим группу [math]displaystyle{ U(mathbb{Z}/9mathbb{Z}) }[/math]
-
-
- [math]displaystyle{ U(mathbb{Z}/9mathbb{Z}) }[/math] = {1,2,4,5,7,8}
- Генератором группы является число 2.
- [math]displaystyle{ 2^1 equiv 2 pmod 9 }[/math]
- [math]displaystyle{ 2^2 equiv 4 pmod 9 }[/math]
- [math]displaystyle{ 2^3 equiv 8 pmod 9 }[/math]
- [math]displaystyle{ 2^4 equiv 7 pmod 9 }[/math]
- [math]displaystyle{ 2^5 equiv 5 pmod 9 }[/math]
- [math]displaystyle{ 2^6 equiv 1 pmod 9 }[/math]
- Как видим, любой элемент группы [math]displaystyle{ U(mathbb{Z}/9mathbb{Z}) }[/math] может быть представлен в виде [math]displaystyle{ 2^l }[/math], где [math]displaystyle{ 1leell lt varphi(m) }[/math]. То есть группа [math]displaystyle{ U(mathbb{Z}/9mathbb{Z}) }[/math] — циклическая.
-
Общий случай
В общем случае необходимо определение первообразного корня.
Первообразный корень по простому модулю [math]displaystyle{ p }[/math] — это число, которое вместе со своим классом вычетов порождает группу [math]displaystyle{ mathbb{Z}/pmathbb{Z} }[/math].[5]
- Примеры: 2 — первообразный корень по модулю 11; 8 — первообразный корень по модулю 11; 3 не является первообразным корнем по модулю 11.
В случае целого модуля [math]displaystyle{ n }[/math] определение такое же.
Структуру группы определяет следующая теорема: Если p — нечётное простое число и k — целое положительное, то существуют первообразные корни по модулю [math]displaystyle{ p^{k} }[/math], то есть [math]displaystyle{ mathbb{Z}/p^{k}mathbb{Z} }[/math] — циклическая группа.
Из китайской теоремы об остатках следует, что при [math]displaystyle{ n=p_1^{a_1}p_2^{a_2}…p_l^{a_l} }[/math] имеет место изоморфизм [math]displaystyle{ U(mathbb{Z}/nmathbb{Z}) }[/math] ≈ [math]displaystyle{ U(mathbb{Z}/p_1^{a_1}mathbb{Z})times U(mathbb{Z}/p_2^{a_2}mathbb{Z})times dots U(mathbb{Z}/p_l^{a_l}mathbb{Z}) }[/math].
Группа [math]displaystyle{ U(mathbb{Z}/p_i^{a_i}mathbb{Z}) }[/math] — циклическая. Её порядок равен [math]displaystyle{ p_i^{a_i-1}(p_i-1) }[/math].
Группа [math]displaystyle{ U(mathbb{Z}/2^{a}mathbb{Z}) }[/math] — также циклическая порядка a при a=1 или a=2. При [math]displaystyle{ a geqslant 3 }[/math] эта группа циклической не является и представляет собой прямое произведение двух циклических групп, порядков [math]displaystyle{ 2 }[/math] и [math]displaystyle{ 2^{a-2} }[/math].
Группа [math]displaystyle{ U(mathbb{Z}/nmathbb{Z}) }[/math] циклична тогда и только тогда, когда [math]displaystyle{ n=p^a }[/math] или [math]displaystyle{ n=2p^a }[/math] или n = 2 или n = 4, где p — нечётное простое число. В общем случае [math]displaystyle{ U(mathbb{Z}/nmathbb{Z}) }[/math] как абелева группа представляется прямым произведением циклических примарных групп, изоморфных [math]displaystyle{ mathbb{Z}_{u_i}^{+} }[/math].[5]
Подгруппа свидетелей простоты
Пусть [math]displaystyle{ m }[/math] — нечётное число большее 1. Число [math]displaystyle{ m-1 }[/math] однозначно представляется в виде [math]displaystyle{ m-1 = 2^s cdot t }[/math], где [math]displaystyle{ t }[/math] нечётно. Целое число [math]displaystyle{ a }[/math], [math]displaystyle{ 1 lt a lt m }[/math], называется свидетелем простоты числа [math]displaystyle{ m }[/math], если выполняется одно из условий:
- [math]displaystyle{ a^tequiv 1pmod m }[/math]
или
- существует целое число [math]displaystyle{ k }[/math], [math]displaystyle{ 0leq klt s }[/math], такое, что [math]displaystyle{ a^{2^kt}equiv m-1pmod m. }[/math]
Если число [math]displaystyle{ m }[/math] — составное, существует подгруппа мультипликативной группы кольца вычетов, называемая подгруппой свидетелей простоты. Её элементы, возведённые в степень [math]displaystyle{ m-1 }[/math], совпадают с [math]displaystyle{ 1 }[/math] по модулю [math]displaystyle{ m }[/math].
Пример: [math]displaystyle{ m=9 }[/math]. Есть [math]displaystyle{ 6 }[/math] остатков, взаимно простых с [math]displaystyle{ 9 }[/math], это [math]displaystyle{ 1,2,4,5,7 }[/math] и [math]displaystyle{ 8 }[/math]. [math]displaystyle{ 8 }[/math] эквивалентно [math]displaystyle{ -1 }[/math] по модулю [math]displaystyle{ 9 }[/math], значит [math]displaystyle{ 8^{8} }[/math] эквивалентно [math]displaystyle{ 1 }[/math] по модулю [math]displaystyle{ 9 }[/math]. Значит, [math]displaystyle{ 1 }[/math] и [math]displaystyle{ 8 }[/math] — свидетели простоты числа [math]displaystyle{ 9 }[/math]. В данном случае {1, 8} — подгруппа свидетелей простоты.[6]
Свойства
Экспонента группы
Экспонента группы равна функции Кармайкла [math]displaystyle{ lambda(n)= }[/math][math]displaystyle{ textstyle operatorname{lcm} }[/math][math]displaystyle{ (p_1^{a_1-1}(p_1-1),cdots, p_s^{a_s-1}(p_s-1)) }[/math].
Порядок группы
Порядок группы равен функции Эйлера: [math]displaystyle{ |U(mathbb{Z}/mmathbb{Z})|=varphi(m) }[/math]. Отсюда и из изоморфизма [math]displaystyle{ U(mathbb{Z}/mmathbb{Z}) }[/math] ≈ [math]displaystyle{ U(mathbb{Z}/p_1^{a_1}mathbb{Z})times U(mathbb{Z}/p_2^{a_2}mathbb{Z})times … U(mathbb{Z}/p_l^{a_l}mathbb{Z}) }[/math] можно получить ещё один способ доказательства равенства [math]displaystyle{ varphi(m) = varphi(m_1)varphi(m_2)…varphi(m_t) }[/math] при [math]displaystyle{ m = m_1m_2…m_t }[/math] [5]
Порождающее множество
[math]displaystyle{ U(mathbb{Z}/nmathbb{Z}) }[/math] — циклическая группа тогда и только тогда, когда [math]displaystyle{ varphi(n)=lambda(n). }[/math] В случае циклической группы генератор называется первообразным корнем.
Пример
Приведённая система вычетов по модулю [math]displaystyle{ 10 }[/math] состоит из [math]displaystyle{ 4 }[/math] классов вычетов: [math]displaystyle{ [1]_{10}, [3]_{10}, [7]_{10}, [9]_{10} }[/math].
Относительно определённого для классов вычетов умножения они образуют группу, причём [math]displaystyle{ [3]_{10} }[/math] и [math]displaystyle{ [7]_{10} }[/math] взаимно обратны (то есть [math]displaystyle{ [3]_{10}{cdot}[7]_{10} = [1]_{10} }[/math]),
а [math]displaystyle{ [1]_{10} }[/math] и [math]displaystyle{ [9]_{10} }[/math] обратны сами себе.
Структура группы
Запись [math]displaystyle{ C_n }[/math] означает «циклическая группа порядка n».
| [math]displaystyle{ n; }[/math] | [math]displaystyle{ (mathbb{Z}/nmathbb{Z})^times }[/math] | [math]displaystyle{ varphi(n) }[/math] | [math]displaystyle{ lambda(n); }[/math] | Генератор группы | [math]displaystyle{ n; }[/math] | [math]displaystyle{ (mathbb{Z}/nmathbb{Z})^times }[/math] | [math]displaystyle{ varphi(n) }[/math] | [math]displaystyle{ lambda(n); }[/math] | Генератор группы | [math]displaystyle{ n; }[/math] | [math]displaystyle{ (mathbb{Z}/nmathbb{Z})^times }[/math] | [math]displaystyle{ varphi(n) }[/math] | [math]displaystyle{ lambda(n); }[/math] | Генератор группы | [math]displaystyle{ n; }[/math] | [math]displaystyle{ (mathbb{Z}/nmathbb{Z})^times }[/math] | [math]displaystyle{ varphi(n) }[/math] | [math]displaystyle{ lambda(n); }[/math] | Генератор группы | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | C1 | 1 | 1 | 0 | 33 | C2×C10 | 20 | 10 | 2, 10 | 65 | C4×C12 | 48 | 12 | 2, 12 | 97 | C96 | 96 | 96 | 5 | |||
| 2 | C1 | 1 | 1 | 1 | 34 | C16 | 16 | 16 | 3 | 66 | C2×C10 | 20 | 10 | 5, 7 | 98 | C42 | 42 | 42 | 3 | |||
| 3 | C2 | 2 | 2 | 2 | 35 | C2×C12 | 24 | 12 | 2, 6 | 67 | C66 | 66 | 66 | 2 | 99 | C2×C30 | 60 | 30 | 2, 5 | |||
| 4 | C2 | 2 | 2 | 3 | 36 | C2×C6 | 12 | 6 | 5, 19 | 68 | C2×C16 | 32 | 16 | 3, 67 | 100 | C2×C20 | 40 | 20 | 3, 99 | |||
| 5 | C4 | 4 | 4 | 2 | 37 | C36 | 36 | 36 | 2 | 69 | C2×C22 | 44 | 22 | 2, 68 | 101 | C100 | 100 | 100 | 2 | |||
| 6 | C2 | 2 | 2 | 5 | 38 | C18 | 18 | 18 | 3 | 70 | C2×C12 | 24 | 12 | 3, 69 | 102 | C2×C16 | 32 | 16 | 5, 101 | |||
| 7 | C6 | 6 | 6 | 3 | 39 | C2×C12 | 24 | 12 | 2, 38 | 71 | C70 | 70 | 70 | 7 | 103 | C102 | 102 | 102 | 5 | |||
| 8 | C2×C2 | 4 | 2 | 3, 5 | 40 | C2×C2×C4 | 16 | 4 | 3, 11, 39 | 72 | C2×C2×C6 | 24 | 6 | 5, 17, 19 | 104 | C2×C2×C12 | 48 | 12 | 3, 5, 103 | |||
| 9 | C6 | 6 | 6 | 2 | 41 | C40 | 40 | 40 | 6 | 73 | C72 | 72 | 72 | 5 | 105 | C2×C2×C12 | 48 | 12 | 2, 29, 41 | |||
| 10 | C4 | 4 | 4 | 3 | 42 | C2×C6 | 12 | 6 | 5, 13 | 74 | C36 | 36 | 36 | 5 | 106 | C52 | 52 | 52 | 3 | |||
| 11 | C10 | 10 | 10 | 2 | 43 | C42 | 42 | 42 | 3 | 75 | C2×C20 | 40 | 20 | 2, 74 | 107 | C106 | 106 | 106 | 2 | |||
| 12 | C2×C2 | 4 | 2 | 5, 7 | 44 | C2×C10 | 20 | 10 | 3, 43 | 76 | C2×C18 | 36 | 18 | 3, 37 | 108 | C2×C18 | 36 | 18 | 5, 107 | |||
| 13 | C12 | 12 | 12 | 2 | 45 | C2×C12 | 24 | 12 | 2, 44 | 77 | C2×C30 | 60 | 30 | 2, 76 | 109 | C108 | 108 | 108 | 6 | |||
| 14 | C6 | 6 | 6 | 3 | 46 | C22 | 22 | 22 | 5 | 78 | C2×C12 | 24 | 12 | 5, 7 | 110 | C2×C20 | 40 | 20 | 3, 109 | |||
| 15 | C2×C4 | 8 | 4 | 2, 14 | 47 | C46 | 46 | 46 | 5 | 79 | C78 | 78 | 78 | 3 | 111 | C2×C36 | 72 | 36 | 2, 110 | |||
| 16 | C2×C4 | 8 | 4 | 3, 15 | 48 | C2×C2×C4 | 16 | 4 | 5, 7, 47 | 80 | C2×C4×C4 | 32 | 4 | 3, 7, 79 | 112 | C2×C2×C12 | 48 | 12 | 3, 5, 111 | |||
| 17 | C16 | 16 | 16 | 3 | 49 | C42 | 42 | 42 | 3 | 81 | C54 | 54 | 54 | 2 | 113 | C112 | 112 | 112 | 3 | |||
| 18 | C6 | 6 | 6 | 5 | 50 | C20 | 20 | 20 | 3 | 82 | C40 | 40 | 40 | 7 | 114 | C2×C18 | 36 | 18 | 5, 37 | |||
| 19 | C18 | 18 | 18 | 2 | 51 | C2×C16 | 32 | 16 | 5, 50 | 83 | C82 | 82 | 82 | 2 | 115 | C2×C44 | 88 | 44 | 2, 114 | |||
| 20 | C2×C4 | 8 | 4 | 3, 19 | 52 | C2×C12 | 24 | 12 | 7, 51 | 84 | C2×C2×C6 | 24 | 6 | 5, 11, 13 | 116 | C2×C28 | 56 | 28 | 3, 115 | |||
| 21 | C2×C6 | 12 | 6 | 2, 20 | 53 | C52 | 52 | 52 | 2 | 85 | C4×C16 | 64 | 16 | 2, 3 | 117 | C6×C12 | 72 | 12 | 2, 17 | |||
| 22 | C10 | 10 | 10 | 7 | 54 | C18 | 18 | 18 | 5 | 86 | C42 | 42 | 42 | 3 | 118 | C58 | 58 | 58 | 11 | |||
| 23 | C22 | 22 | 22 | 5 | 55 | C2×C20 | 40 | 20 | 2, 21 | 87 | C2×C28 | 56 | 28 | 2, 86 | 119 | C2×C48 | 96 | 48 | 3, 118 | |||
| 24 | C2×C2×C2 | 8 | 2 | 5, 7, 13 | 56 | C2×C2×C6 | 24 | 6 | 3, 13, 29 | 88 | C2×C2×C10 | 40 | 10 | 3, 5, 7 | 120 | C2×C2×C2×C4 | 32 | 4 | 7, 11, 19, 29 | |||
| 25 | C20 | 20 | 20 | 2 | 57 | C2×C18 | 36 | 18 | 2, 20 | 89 | C88 | 88 | 88 | 3 | 121 | C110 | 110 | 110 | 2 | |||
| 26 | C12 | 12 | 12 | 7 | 58 | C28 | 28 | 28 | 3 | 90 | C2×C12 | 24 | 12 | 7, 11 | 122 | C60 | 60 | 60 | 7 | |||
| 27 | C18 | 18 | 18 | 2 | 59 | C58 | 58 | 58 | 2 | 91 | C6×C12 | 72 | 12 | 2, 3 | 123 | C2×C40 | 80 | 40 | 7, 83 | |||
| 28 | C2×C6 | 12 | 6 | 3, 13 | 60 | C2×C2×C4 | 16 | 4 | 7, 11, 19 | 92 | C2×C22 | 44 | 22 | 3, 91 | 124 | C2×C30 | 60 | 30 | 3, 61 | |||
| 29 | C28 | 28 | 28 | 2 | 61 | C60 | 60 | 60 | 2 | 93 | C2×C30 | 60 | 30 | 11, 61 | 125 | C100 | 100 | 100 | 2 | |||
| 30 | C2×C4 | 8 | 4 | 7, 11 | 62 | C30 | 30 | 30 | 3 | 94 | C46 | 46 | 46 | 5 | 126 | C6×C6 | 36 | 6 | 5, 13 | |||
| 31 | C30 | 30 | 30 | 3 | 63 | C6×C6 | 36 | 6 | 2, 5 | 95 | C2×C36 | 72 | 36 | 2, 94 | 127 | C126 | 126 | 126 | 3 | |||
| 32 | C2×C8 | 16 | 8 | 3, 31 | 64 | C2×C16 | 32 | 16 | 3, 63 | 96 | C2×C2×C8 | 32 | 8 | 5, 17, 31 | 128 | C2×C32 | 64 | 32 | 3, 127 |
Применение
На сложности дискретного логарифмирования в мультипликативной группе кольца вычетов основана криптографическая стойкость шифрсистемы Эль-Гамаля.[7]
История
Вклад в исследование структуры мультипликативной группы кольца вычетов внесли Артин, Билхарц, Брауэр, Вильсон, Гаусс, Лагранж, Лемер, Варинг, Ферма, Хули, Эйлер.
Лагранж доказал лемму о том, что если [math]displaystyle{ f(x) in k[x] }[/math], и k — поле, то f имеет не более n различных корней, где n — степень f. Он же доказал важное следствие этой леммы, заключающееся в сравнении [math]displaystyle{ x^{p-1}-1 }[/math] ≡ [math]displaystyle{ (x-1)(x-2)…(x-p+1)mod(p) }[/math]. Эйлер доказал малую теорему Ферма. Варинг сформулировал теорему Вильсона, а Лагранж её доказал. Эйлер предположил существование примитивных корней по модулю простого числа. Гаусс это доказал. Артин выдвинул свою гипотезу о существовании и количественной оценке простых чисел, по модулю которых заданное целое число является первообразным корнем. Брауэр внес вклад в исследование проблемы существования наборов последовательных целых чисел, каждое из которых — k-ая степень по модулю p. Билхарц доказал аналог гипотезы Артина. Хули доказал гипотезу Артина с предположением справедливости расширенной гипотезы Римана в полях алгебраических чисел.[5]
Примечания
- ↑ 1,0 1,1 И. М. Виноградов Основы теории чисел. изд. 9-е, перераб., М. : Наука. 1981
- ↑ Сагалович Ю. Л. Введение в алгебраические коды. 2011.
- ↑ Бухштаб, 1966.
- ↑ 4,0 4,1 4,2 4,3 В. Босс Лекции по математике. Том 14. Теория чисел. 2014.
- ↑ 5,0 5,1 5,2 5,3 5,4 Айерлэнд, Роузен, 1987.
- ↑ Erdős, Paul; Pomerance, Carl. On the number of false witnesses for a composite number (англ.) // Math. Comput.[en] : journal. — 1986. — Vol. 46. — P. 259—279.
- ↑ Алферов и др., 2002.
Литература
- Айерлэнд К., Роузен М. Классическое введение в современную теорию чисел. — М.: Мир, 1987.
- Алферов А.П., Зубов А.Ю., Кузьмин А.С. Черемушкин А.В. Основы криптографии. — Москва: «Гелиос АРВ», 2002.
- Ростовцев А.Г., Маховенко Е.Б. Теоретическая криптография. — Санкт-Петербург: НПО «Профессионал», 2004.
Ссылки
- Бухштаб А. А. Теория чисел. — М.: Просвещение, 1966.
- Weisstein, Eric W. Modulo Multiplication Group (англ.) на сайте Wolfram MathWorld.
Как правило, наиболее распространёнными формами записи бинарной операции в группе являются аддитивная: + и мультипликативная: •.
Аддитивная запись бинарной операции
Если в группе
бинарная операция
является операцией сложения, то данная группа называется
аддитивной группой
и обозначается
.
Примеры аддитивных групп
-
Любое кольцо или поле является группой относительно операции сложения (определённой в этом кольце). Данная группа называется аддитивной группой кольца или поля соответственно.
Рассмотрим несколько примеров аддитивных групп: -
–
аддитивная группа всех геометрических векторов в пространстве.
Мультипликативная запись бинарной операции
Если в группе
бинарная операция
является операцией умножения, то данная группа называется
мультипликативной группой
и обозначается
.
Замечание
Также существуют мультипликативные группы колец или полей. Для рассмотрения примеров таких групп сначала дадим определения некоторых терминов.
Определение обратимого элемента в кольце.
Пусть
– ассоциативное кольцо с 1, тогда элемент
называется обратимым, если существует элемент
такой, что:
, причём элемент
b = a−1.
Обозначение.
Множество всех обратимых элементов кольца
обозначается, как
.
Следствие.
В поле
обратимыми элементами являются все элементы, кроме 0. То есть
.
Примеры мультипликативных групп
-
Множество всех элементов кроме 0 (нейтрального элемента относительно операции сложения) поля
является группой относительно операции умножения (определённой в данном поле). Данная группа называется мультипликативной группой поля и обозначается
.
Рассмотрим несколько примеров мультипликативных групп поля: -
Множество всех обратимых элементов ассоциативного кольца с 1 –
является группой относительно операции умножения (определённой в этом кольце). Данная группа называется мультипликативной группой кольца и обозначается
.
Рассмотрим несколько примеров мультипликативных групп колец: -
–
группа всех обратимых (невырожденных) квадратных матриц размера n×n относительно операции
умножения матриц.
Данная группа называется
общей линейной группой
и согласно определению выглядит следующим образом:
.
Напомним, что матрица называется невырожденной или обратимой, если её определитель не равен 0.
–
в круглых скобках означает, что элементами матрицы X являются действительные числа. Более подробно данная группа будет разобрана в следующих статьях.
Приведённая система вычетов по модулю m — множество всех чисел полной системы вычетов по модулю m, взаимно простых с m. Приведённая система вычетов по модулю m состоит из φ(m) чисел, где φ(·) — функция Эйлера.
В качестве приведённой системы вычетов по модулю m обычно берутся взаимно простые с m числа от 1 до m-1.
Приведённая система вычетов с умножением по модулю m образует группу, называемую мультипликативной группой или группой обратимых элементов кольца вычетов по модулю m, которая обозначается  или
или  .
.
Содержание
- 1 Аксиоматика группы
- 2 Простейший случай
- 3 Общий случай
- 4 Формы записи
- 5 Подгруппа свидетелей простоты
- 6 Свойства
- 6.1 Экспонента группы
- 6.2 Порядок группы
- 6.3 Порождающее множество
- 7 Пример
- 8 Структура группы
- 9 Применение
- 10 История
- 11 Примечания
- 12 Литература
- 13 Ссылки
Аксиоматика группы
Легко показать, что группа классов взаимнопростых с n вычетов по умножению удовлетворяет аксиоматике абелевой группы. Т.к. сравнение a ≡ b (mod n) предполагает равенство НОД(a,n)=НОД(b,n), то понятие эквивалентных классов вычетов по модулю n, взаимно простых с n, четко определено. Т.к. равенства НОД(a,n)=1 и НОД(b,n)=1 предполагают равенство НОД(ab,n)=1, то множество классов вычетов по модулю n, взаимно простых с n, замкнуто относительно умножения. При a, удовлетворяющем равенству НОД(a,n)=1, нахождение x, удовлетворяющего сравнению ax ≡ 1 (mod n), равносильно решению уравнения ax + ny = 1, которое может быть решено путем соотношения Безу. Найденное x будет обладать свойством НОД(x,n)=1.
Простейший случай
Чтобы понять структуру группы  , можно рассмотреть частный случай
, можно рассмотреть частный случай  , где p – простое число, и обобщить его. Рассмотрим простейший случай, когда a=1, т.е.
, где p – простое число, и обобщить его. Рассмотрим простейший случай, когда a=1, т.е.  .
.
Теорема:  — циклическая группа. [1]
— циклическая группа. [1]
Общий случай
Для рассмотрения общего случая необходимо определение примитивного корня. Примитивный корень по простому модулю p – это число, которое вместе со своим классом вычетов порождает группу  . Примеры: 2 — примитивный корень по модулю 11; 8 — примитивный корень по модулю 11; 3 не является примитивным корнем по модулю 11. В случае целого модуля n определение такое же.
. Примеры: 2 — примитивный корень по модулю 11; 8 — примитивный корень по модулю 11; 3 не является примитивным корнем по модулю 11. В случае целого модуля n определение такое же.
Теорема: Если p – нечетное простое число и l – целое положительное, то существуют примитивные корни по модулю  т.е.
т.е.  – циклическая группа. Из китайской теоремы об остатках следует, что при
– циклическая группа. Из китайской теоремы об остатках следует, что при  имеет место изоморфизм
имеет место изоморфизм  ≈
≈  . Группа
. Группа  – циклическая. Ее порядок равен
– циклическая. Ее порядок равен  . Группа
. Группа  – также циклическая. Ее порядок равен a при a=1 или a=2. При
– также циклическая. Ее порядок равен a при a=1 или a=2. При  эта группа есть прямое произведение двух циклических групп, порядков
эта группа есть прямое произведение двух циклических групп, порядков  и
и  . Группа
. Группа  циклична тогда и только тогда, когда
циклична тогда и только тогда, когда  или
или  или n = 2 или n = 4, где p — нечётное простое число. В общем случае
или n = 2 или n = 4, где p — нечётное простое число. В общем случае  как абелева группа представляется прямым произведением циклических примарных групп, изоморфных
как абелева группа представляется прямым произведением циклических примарных групп, изоморфных  . [1]
. [1]
Формы записи
Кольцо вычетов по модулю n обозначают  или
или  . Мультипликативную группу кольца вычетов обозначают
. Мультипликативную группу кольца вычетов обозначают 


 ,
,  ,
,  .
.
Подгруппа свидетелей простоты
Пусть  — нечётное число большее 1. Число
— нечётное число большее 1. Число  однозначно представляется в виде
однозначно представляется в виде  , где
, где  нечётно. Целое число
нечётно. Целое число  ,
,  , называется свидетелем простоты числа
, называется свидетелем простоты числа  , если выполняется одно из условий:
, если выполняется одно из условий:
или
Если число n – составное, существует подгруппа мультипликативной группы кольца вычетов, называемая подгруппой свидетелей простоты. Ее элементы, возведенные в степень n-1, совпадают с 1 по модулю n. Пример: n=9 Есть 6 остатков, взаимно простых с 9, это 1,2,4,5,7 и 8. 8 эквивалентно -1 по модулю 9, значит  эквивалентно 1 по модулю 9. Значит, 1 и 8 — свидетели простоты числа 9. В данном случае {1, 8} — подгруппа свидетелей простоты.
эквивалентно 1 по модулю 9. Значит, 1 и 8 — свидетели простоты числа 9. В данном случае {1, 8} — подгруппа свидетелей простоты.
Свойства
Экспонента группы
Экспонента группы равна функции Кармайкла (англ.): для нечетных m она равна  , а для чётных — в 2 раза меньше.
, а для чётных — в 2 раза меньше.
Порядок группы
Порядок группы равен функции Эйлера: 
Порождающее множество
 – циклическая группа тогда и только тогда, когда
– циклическая группа тогда и только тогда, когда  В случае циклической группы генератор называется первообразным корнем.
В случае циклической группы генератор называется первообразным корнем.
Пример
Приведённая система вычетов по модулю 10 состоит из 4 классов вычетов: ![[1]_{10}, [3]_{10}, [7]_{10}, [9]_{10}](https://dic.academic.ru/dic.nsf/ruwiki/d514f69b81c3cbb699f42840fe028590.png) . Относительно определённого для классов вычетов умножения они образуют группу, причём
. Относительно определённого для классов вычетов умножения они образуют группу, причём ![[3]_{10}](https://dic.academic.ru/dic.nsf/ruwiki/4873e7f47b0f49f33cf8612226637975.png) и
и ![[7]_{10}](https://dic.academic.ru/dic.nsf/ruwiki/800a582281edaef36f9b56f8cc68d849.png) взаимно обратны (то есть
взаимно обратны (то есть ![[3]_{10}{cdot}[7]_{10} = [1]_{10}](https://dic.academic.ru/dic.nsf/ruwiki/d2bffcd64fe82ce0131b2eb10955f110.png) ), а
), а ![[1]_{10}](https://dic.academic.ru/dic.nsf/ruwiki/8bd3bb2ffc59ba2362e31f93a7ed5a03.png) и
и ![[9]_{10}](https://dic.academic.ru/dic.nsf/ruwiki/f9b9f7d026cf4f09c246abb6da399360.png) обратны сами себе.
обратны сами себе.
Структура группы
Запись  означает «циклическая группа порядка n».
означает «циклическая группа порядка n».
 |
 |
 |
 |
генератор |  |
 |
 |
 |
генератор | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | C1 | 1 | 1 | 1 | 33 | C2×C10 | 20 | 10 | 10, 2 | |
| 3 | C2 | 2 | 2 | 2 | 34 | C16 | 16 | 16 | 3 | |
| 4 | C2 | 2 | 2 | 3 | 35 | C2×C12 | 24 | 12 | 6, 2 | |
| 5 | C4 | 4 | 4 | 2 | 36 | C2×C6 | 12 | 6 | 19, 5 | |
| 6 | C2 | 2 | 2 | 5 | 37 | C36 | 36 | 36 | 2 | |
| 7 | C6 | 6 | 6 | 3 | 38 | C18 | 18 | 18 | 3 | |
| 8 | C2×C2 | 4 | 2 | 7, 3 | 39 | C2×C12 | 24 | 12 | 38, 2 | |
| 9 | C6 | 6 | 6 | 2 | 40 | C2×C2×C4 | 16 | 4 | 39, 11, 3 | |
| 10 | C4 | 4 | 4 | 3 | 41 | C40 | 40 | 40 | 6 | |
| 11 | C10 | 10 | 10 | 2 | 42 | C2×C6 | 12 | 6 | 13, 5 | |
| 12 | C2×C2 | 4 | 2 | 5, 7 | 43 | C42 | 42 | 42 | 3 | |
| 13 | C12 | 12 | 12 | 2 | 44 | C2×C10 | 20 | 10 | 43, 3 | |
| 14 | C6 | 6 | 6 | 3 | 45 | C2×C12 | 24 | 12 | 44, 2 | |
| 15 | C2×C4 | 8 | 4 | 14, 2 | 46 | C22 | 22 | 22 | 5 | |
| 16 | C2×C4 | 8 | 4 | 15, 3 | 47 | C46 | 46 | 46 | 5 | |
| 17 | C16 | 16 | 16 | 3 | 48 | C2×C2×C4 | 16 | 4 | 47, 7, 5 | |
| 18 | C6 | 6 | 6 | 5 | 49 | C42 | 42 | 42 | 3 | |
| 19 | C18 | 18 | 18 | 2 | 50 | C20 | 20 | 20 | 3 | |
| 20 | C2×C4 | 8 | 4 | 19, 3 | 51 | C2×C16 | 32 | 16 | 50, 5 | |
| 21 | C2×C6 | 12 | 6 | 20, 2 | 52 | C2×C12 | 24 | 12 | 51, 7 | |
| 22 | C10 | 10 | 10 | 7 | 53 | C52 | 52 | 52 | 2 | |
| 23 | C22 | 22 | 22 | 5 | 54 | C18 | 18 | 18 | 5 | |
| 24 | C2×C2×C2 | 8 | 2 | 5, 7, 13 | 55 | C2×C20 | 40 | 20 | 21, 2 | |
| 25 | C20 | 20 | 20 | 2 | 56 | C2×C2×C6 | 24 | 6 | 13, 29, 3 | |
| 26 | C12 | 12 | 12 | 7 | 57 | C2×C18 | 36 | 18 | 20, 2 | |
| 27 | C18 | 18 | 18 | 2 | 58 | C28 | 28 | 28 | 3 | |
| 28 | C2×C6 | 12 | 6 | 13, 3 | 59 | C58 | 58 | 58 | 2 | |
| 29 | C28 | 28 | 28 | 2 | 60 | C2×C2×C4 | 16 | 4 | 11, 19, 7 | |
| 30 | C2×C4 | 8 | 4 | 11, 7 | 61 | C60 | 60 | 60 | 2 | |
| 31 | C30 | 30 | 30 | 3 | 62 | C30 | 30 | 30 | 3 | |
| 32 | C2×C8 | 16 | 8 | 31, 3 | 63 | C6×C6 | 36 | 6 | 2, 5 |
Применение
На сложности дискретного логарифмирования в мультипликативной группе кольца вычетов основана криптографическая стойкость шифрсистемы Эль-Гамаля.
История
Вклад в исследование структуры мультипликативной группы кольца вычетов внесли Артин, Билхарц, Брауэр, Варинг, Вильсон, Гаусс, Лагранж, Лемер, Ферма, Хули, Эйлер. Лагранж доказал лемму о том, что если ![f(x) in k[x]](https://dic.academic.ru/dic.nsf/ruwiki/5b2703f2563ff12348128f782553bbd2.png) , и k – поле, то f имеет не более n различных корней, где n – степень f. Он же доказал важное следствие этой леммы, заключающееся в сравнении
, и k – поле, то f имеет не более n различных корней, где n – степень f. Он же доказал важное следствие этой леммы, заключающееся в сравнении  ≡ (x-1)(x-2)…(x-p+1)mod(p). Эйлер доказал малую теорему Ферма. Варинг сформулировал теорему Вильсона, а Лагранж ее доказал. Эйлер предположил существование примитивных корней по модулю простого числа. Гаусс это доказал. Артин выдвинул свою гипотезу о существовании и количественной оценке простых чисел, по модулю которых заданное целое число является первообразным корнем. Брауэр внес вклад в исследование проблемы существования наборов последовательных целых чисел, каждое из которых — k-ая степень по модулю p. Билхарц доказал аналог гипотезы Артина. Хули доказал гипотезу Артина с предположением справедливости расширенной гипотезы Римана в полях алгебраических чисел.[1]
≡ (x-1)(x-2)…(x-p+1)mod(p). Эйлер доказал малую теорему Ферма. Варинг сформулировал теорему Вильсона, а Лагранж ее доказал. Эйлер предположил существование примитивных корней по модулю простого числа. Гаусс это доказал. Артин выдвинул свою гипотезу о существовании и количественной оценке простых чисел, по модулю которых заданное целое число является первообразным корнем. Брауэр внес вклад в исследование проблемы существования наборов последовательных целых чисел, каждое из которых — k-ая степень по модулю p. Билхарц доказал аналог гипотезы Артина. Хули доказал гипотезу Артина с предположением справедливости расширенной гипотезы Римана в полях алгебраических чисел.[1]
Примечания
- ↑ 1 2 3 Айерлэнд. Роузен. Классическое введение в современную теорию чисел.
Литература
- Айерлэнд К., Роузен М. Классическое введение в современную теорию чисел. — М.: Мир, 1987.
- Алферов А.П., Зубов А.Ю., Кузьмин А.С. Черемушкин А.В. Основы криптографии. — Москва: «Гелиос АРВ», 2002.
- Ростовцев А.Г., Маховенко Е.Б. Теоретическая криптография. — Санкт-Петербург: НПО «Профессионал», 2004.
Ссылки
- Бухштаб А. А. Теория чисел. — М.: Просвещение, 1966.
- Weisstein, Eric W. Modulo Multiplication Group (англ.) на сайте Wolfram MathWorld.
3.1.5 Конечные кольца и поля
Определение 3.18 Множество  с двумя алгебраическими операциями
с двумя алгебраическими операциями 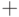 ,
, 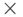 называется ассоциативным кольцом, если в нём выполняются свойства:
называется ассоциативным кольцом, если в нём выполняются свойства:
 является коммутативной группой по сложению с нейтральным элементом
является коммутативной группой по сложению с нейтральным элементом  (эта группа называется аддитивной).
(эта группа называется аддитивной).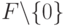 является полугруппой (обозначается
является полугруппой (обозначается 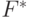 ).
).- Дистрибутивность:
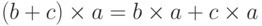 и
и 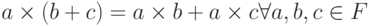 .
.
Определение 3.19 Кольца  и
и  называются изоморфными, если существует отображение
называются изоморфными, если существует отображение  , являющееся изоморфизмом аддитивных и мультипликативных групп этих колец.
, являющееся изоморфизмом аддитивных и мультипликативных групп этих колец.
Определение 3.20 Полем называется кольцо  , в котором
, в котором 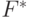 является коммутативной группой.
является коммутативной группой.
Определение 3.21 Характеристикой поля называется наименьшее такое натуральное число  , что
, что 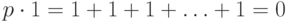 , или 0, если такого
, или 0, если такого  не существует. Характеристика поля может быть только простым числом или нулем.
не существует. Характеристика поля может быть только простым числом или нулем.
Определение 3.22 Левым (правым) идеалом кольца называется любое его подкольцо, выдерживающее умножение слева (соответственно, справа) на любой элемент кольца. Подкольцо, являющееся левым и правым идеалом, называется двусторонним идеалом, или просто идеалом.
Подкольцо  разбивает кольцо
разбивает кольцо  на классы эквивалентности:
на классы эквивалентности: 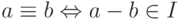 . Класс, содержащий элемент
. Класс, содержащий элемент  , можно записать в виде:
, можно записать в виде:
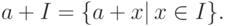
Если подкольцо является идеалом, то на множестве таких классов можно ввести операции сложения и умножения, относительно которых множество классов образует кольцо, называемое фактор-кольцом:
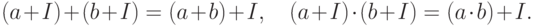
Из определения идеала следует, что результат операций не зависит от выбора представителей  ,
,  , то есть операции заданы корректно.
, то есть операции заданы корректно.
Наиболее важными для нас будут следующие кольца и поля:
- Кольцо целых чисел
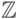 относительно обыкновенных операций сложения и умножения.
относительно обыкновенных операций сложения и умножения. - Поле рациональных чисел
 относительно операций сложения и умножения.
относительно операций сложения и умножения. - Фактор-кольцо
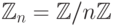 кольца целых чисел по идеалу всех чисел, кратных
кольца целых чисел по идеалу всех чисел, кратных  . Также это кольцо можно себе представлять, как кольцо целых неотрицательных чисел, меньших
. Также это кольцо можно себе представлять, как кольцо целых неотрицательных чисел, меньших  , с операцией сложения и умножения по модулю
, с операцией сложения и умножения по модулю  . Такое кольцо является полем тогда и только тогда, когда
. Такое кольцо является полем тогда и только тогда, когда  – простое число.
– простое число. - Кольцо
![F[{x_1,{dots}, x_n}]](https://intuit.ru/sites/default/files/tex_cache/5830bd1f7c4224bdde9427103672e170.png) многочленов от переменных
многочленов от переменных 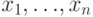 над произвольным полем
над произвольным полем  .
. - Фактор-кольцо
![F[{x}] / f(x) F[x]](https://intuit.ru/sites/default/files/tex_cache/00d09f4ebf7f7e40fc59b3267bf73e48.png) кольца многочленов над полем
кольца многочленов над полем  по идеалу, порожденному одним многочленом
по идеалу, порожденному одним многочленом 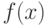 степени
степени  , то есть состоящему из всех многочленов, кратных
, то есть состоящему из всех многочленов, кратных  . Это кольцо можно также рассматривать, как кольцо многочленов степени меньше
. Это кольцо можно также рассматривать, как кольцо многочленов степени меньше  с операцией сложения и умножения по модулю
с операцией сложения и умножения по модулю  . Такое кольцо является полем тогда и только тогда, когда многочлен
. Такое кольцо является полем тогда и только тогда, когда многочлен  неприводим над
неприводим над  .
.
В криптографии нас будут интересовать больше всего конечные поля, то есть поля с конечным множеством  . Перечислим наиболее важные для нас свойства:
. Перечислим наиболее важные для нас свойства:
- Каждое конечное поле имеет простую характеристику
 .
. - Поле простого порядка не имеет подполей, и называется простым.
- Конечное поле характеристики
 содержит подполе порядка
содержит подполе порядка  .
. - Конечное поле является линейным пространством над своим простым подполем, поэтому имеет порядок
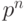 для некоторого натурального числа
для некоторого натурального числа  .
. - Мультипликативная группа конечного поля циклическая. Если поле имеет простой порядок
 , то порождающий его мультипликативную группу элемент называется примитивным корнем по модулю
, то порождающий его мультипликативную группу элемент называется примитивным корнем по модулю  .
. - Конечные поля одного порядка изоморфны.
Рассмотрим несколько связанных с кольцами вычетов задач, часто возникающих в криптографии.
Пример 3.5 Найти мультипликативный порядок элемента 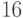 по модулю
по модулю 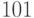 , то есть порядок элемента
, то есть порядок элемента 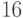 мультипликативной группы
мультипликативной группы  .
.
Решение. Поскольку число 101 простое, порядок мультипликативной группы поля  равен 100. По следствию из теоремы Лагранжа, мультипликативный порядок любого числа по модулю 101 является делителем 100, то есть одним из чисел: 1, 2, 4, 5, 10, 20, 25, 50, 100. Проверим каждое из чисел:
равен 100. По следствию из теоремы Лагранжа, мультипликативный порядок любого числа по модулю 101 является делителем 100, то есть одним из чисел: 1, 2, 4, 5, 10, 20, 25, 50, 100. Проверим каждое из чисел:
 |
1 | 2 | 4 | 5 | 10 | 20 | 25 | 50 | 100 |
|---|---|---|---|---|---|---|---|---|---|
 |
16 | 54 | 88 | 95 | 36 | 84 | 1 | – | – |
После того, как обнаружили, что 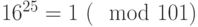 , возводить в
, возводить в 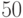 -ю и
-ю и  -ю степень излишне – видно, что наименьшая степень, в которой 16 даст единицу по модулю 101, это 25.
-ю степень излишне – видно, что наименьшая степень, в которой 16 даст единицу по модулю 101, это 25.
Пример 3.6 Найти случайный примитивный корень по модулю  .
.
Решение. Порядок мультипликативной группы поля вычетов по модулю 883 равен 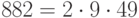 . Будем выбирать случайное число
. Будем выбирать случайное число  и возводить его в степени
и возводить его в степени  ,
,  ,
,  . Если в какой-то степени
. Если в какой-то степени  даст единицу, то его порядок меньше 882, и, следовательно, он не является примитивным корнем по модулю 883. Наоборот, порядок порождающего элемента является делителем числа 882, и если он не является делителем ни одного из чисел
даст единицу, то его порядок меньше 882, и, следовательно, он не является примитивным корнем по модулю 883. Наоборот, порядок порождающего элемента является делителем числа 882, и если он не является делителем ни одного из чисел  ,
,  ,
,  , то равен 882. В первой колонке таблицы приводятся случайно выбранные элементы
, то равен 882. В первой колонке таблицы приводятся случайно выбранные элементы  , а в следующих колонках – результаты возведения в степень.
, а в следующих колонках – результаты возведения в степень.
Итак, 326 является примитивным корнем по модулю 883.










