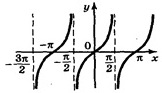
- Развертка тангенса движения точки по числовой окружности в функцию от угла
- Свойства функции y=tgx
- Примеры
п.1. Развертка тангенса движения точки по числовой окружности в функцию от угла
При движении точки по числовой окружности на вертикальной касательной, проведенной через точку (1;0), отображаются значения тангенсов соответствующих углов (см. §3 данного справочника).
Рассмотрим, как изменяется тангенс, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=tgx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривые продолжатся вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривые продолжатся влево.
В результате получаем график y=tgx для для всех x из области допустимых значений.
График y=tgx называют тангенцоидой.
Часть тангенцоиды c (-fracpi2lt xlt fracpi2) называют главной ветвью тангенцоиды.
п.2. Свойства функции y=tgx
1. Область определения (xnefracpi2+pi k) – множество действительных чисел, кроме точек, в которых (cosx=0).
2. Функция не ограничена сверху и снизу. Область значений (yinmathbb{R})
3. Функция нечётная $$ tg(-x)=-tgx $$
4. Функция периодическая с периодом π $$ tg(x+pi k)=tgx $$
5. Функция стремится к (+infty) при приближении слева к точкам (x=fracpi2+pi k).
Приближение к точке a слева записывается как (xrightarrow a-0) $$ lim_{xrightarrowfracpi2+pi k-0} tgx=+infty $$ Функция стремится к (-infty) при приближении справа к точкам (x=fracpi2+pi k).
Приближение к точке a справа записывается как (xrightarrow a+0) $$ lim_{xrightarrowfracpi2+pi k+0} tgx=-infty $$ Нули функции (y_{0}=0) достигаются в точках (x_0=pi k)
6. Функция возрастает на всей области определения.
7. Функция имеет разрывы в точках (x=fracpi2+pi k), через эти точки проходят вертикальные асимптоты. На интервалах между асимптотами (left(-fracpi2+pi k; fracpi2+pi kright)) функция непрерывна.
п.3. Примеры
Пример 1.Найдите наименьшее и наибольшее значение функции y=tgx на заданном промежутке:
a) (left[frac{2pi}{3}; frac{3pi}{2}right)) $$ y_{min}=tgleft(frac{2pi}{3}right)=-sqrt{3}, y_{max}=lim_{xrightarrowfrac{3pi}{2}-0}tgx=+infty $$ б) (left(frac{pi}{2}; piright]) $$ y_{min}=lim_{xrightarrowfrac{pi}{2}+0}tgx=-infty, y_{max}=tg(pi)=0 $$ в) (left[frac{3pi}{4}; frac{7pi}{6}right]) $$ y_{min}=tgleft(frac{3pi}{4}right)=-1, y_{max}=tgleft(frac{7pi}{6}right)=frac{1}{sqrt{3}} $$
Пример 2. Решите уравнение:
a) (tgx=-sqrt{3})
Бесконечное множество решений: (x=frac{2pi}{3}+pi k, kinmathbb{Z})
б) (tgleft(x-fracpi2right)=0)
(x-fracpi2=pi k)
Бесконечное множество решений: (x=frac{pi}{2}+pi k, kinmathbb{Z})
в) (tg(2x)=1)
(2x=fracpi4+pi k)
Бесконечное множество решений: (x=frac{pi}{8}+frac{pi k}{2}, kinmathbb{Z})
г) (tgleft(frac{x}{3}-1right)=-1)
(frac{x}{3}-1=-frac{pi}{4}+pi k)
(frac{x}{3}=1-frac{pi}{4}+pi k)
Бесконечное множество решений: (x=3-frac{3pi}{4}+3pi k, kinmathbb{Z})
Пример 3. Определите чётность функции: a) (y(x)=4tgx+5sinx)
$$ y(-x)=4tg(-x)+5sin(-x)=-4tgx-5sinx=-(4tgx+5sinx)=-y(x) $$ Функция нечётная.
б) (y(x)=tgx-2cosx)
$$ y(-x)=tg(-x)-2cos(-x)=-tgx-2cosx=-(tgx+2cosx)ne left[ begin{array} -y(x)\ y(x) end{array} right. $$ Функция ни чётная, ни нечётная.
в) (y(x)=tg^2x+cos5x)
$$ y(-x)=tg^2(-x)+cos(-5x)=(-tgx)^2+cos5x=tg^2x+cos5x)=y(x) $$ Функция чётная.
г) (y(x)=x^2-tgx)
$$ y(-x)=(-x)^2-tg(-x)=x^2+tgxne left[ begin{array} -y(x)\ y(x) end{array} right. $$ Функция ни чётная, ни нечётная.
Пример 4. Если (tg(7pi-x)=frac34), то чему равны (tgx, ctgx)?
Т.к. период тангенса равен π, получаем: begin{gather*} tg(7pi-x)=tg(-x)=-tgx=frac34Rightarrow tgx=-frac34\ ctgx=frac{1}{tgx}=-frac43 end{gather*} Ответ: (-frac34, -frac43)
Объяснение и обоснование
Напомним, что . Таким образом, областью определения функции y=будут все значения аргумента, при которых , то есть все значения x, kZ. Получаем
Этот результат можно получить и геометрически. Значения тангенса – это ордината соответствующей точки на линии тангенсов (рис.91). Поскольку точки Aи B единичной окружности лежат на прямых ОА и ОВ, параллельных линии тангенсов, мы не сможем найти значение тангенса дляx, kZ.
Для всех других значений аргумента мы можем найти соответствующую точку на линии тангенсов и ее ординату — тангенс. Следовательно, все
Значенияx входят в область определения функции y=tgx.
Для точек единичной окружности (которые не совпадают с точками А и В) ординаты соответствующих т
очек на линии тангенсов принимают
все значения до +, поскольку для любого действительного числа
мы можем указать соответствующую точку на оси ординат, а значит, и соответствующую точку на оси тангенсов. Учитывая, что точка О лежит
внутри окружности, а точка вне ее (или на самой окружности), получаем, что прямая имеет с окружностью хотя бы одну общую точку
(на самом деле их две). Следовательно, для любого действительного числа
найдется аргумент х, такой, что tan x равен данному действительному числу.
Поэтому область значений функции y= tg x – все действительные числа,
то есть R. Это можно записать так: E (=tgx) = R. Отсюда следует, что наибольшего и наименьшего значений функция tan x не имеет.
Как было показано в § 13, тангенс — нечетная функция:tg(-x)=tg x, следовательно, ее график симметричен относительно начала координат.
Тангенс — периодическая функция с наименьшим положительным периодом
Поэтому при построении графика
этой функции достаточно построить график на любом промежутке длиной π,
а потом полученную линию перенести параллельно вправо и влево вдоль оси
Ox на расстоянияkT = πk, где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат,
напомним, что на оси Oy значение x = 0. Тогда соответствующее значение
y = tg 0 = 0, то есть график функции y = tg x проходит через начало координат.
На оси Ox значение y = 0. Поэтому необходимо найти такие значения x,
при которых tg x, то есть ордината соответствующей точки линии тангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при x = πk, k ∈ Z.
Промежутки знакопостоянства. Как было обосновано в § 13, значения
функции тангенс положительны (то есть ордината соответствующей точкилинии тангенсов положительна) в І и ІІІ четвертях. Следовательно, tgx > 0 при
а также, учитывая период, при всех
Значения функции тангенс отрицательны (то есть ордината соответствующей точки линии тангенсов отрицательна) во ІІ и ІV четвертях. Такимобразом,
Промежутки возрастания и убывания.
Учитывая периодичность функции tgx (период T = π), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной π,
например на промежутке . Если x (рис. 92), то при увеличении аргумента x (x2>x1) ордината соответствующей точки линии
тангенсов увеличивается (то есть tgx2>tgx1). Таким образом, на этом
промежутке функция tgx возрастает. Учитывая периодичность функции
tgx, делаем вывод, что она возрастает также на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график
функции y = tg x. Учитывая периодичность этой функции (с периодом π),
сначала построим график на любом промежутке длиной π, например на промежутке . Для более точного построения точек графика воспользуемся также тем, что значение тангенса — это ордината соответствующей точки
линии тангенсов. На рисунке 93 показано построение графика функции
y = tg x на промежутке.
Далее, учитывая периодичность тангенса (с периодом π), повторяем вид
графика на каждом промежутке длиной π (то есть параллельно переносим
график вдоль оси Ох на πk, где k — целое число).
Получаем график, приведенный на рисунке 94, который называется тангенсоидой.
14.4. СВОЙСТВА ФУНКЦИИ y = ctg x И ЕЕ ГРАФИК
Объяснение и обоснование
Так как =, то областью определения котангенса будут все значения аргумента, при которых sin х ≠ 0, то есть x ≠ πk, k ∈ Z. Такимобразом,
D (ctg x): x ≠ πk, k ∈ Z.
Тот же результат можно получить, используя геометрическую иллюстрацию. Значение котангенса — это абсцисса соответствующей точки на линии
котангенсов (рис. 95).
Поскольку точки А и В единичной окружности лежат на прямых ОА
и ОВ, параллельных линии котангенсов, мы не можем найти значение котангенса для x = πk, k ∈ Z. Длядругихзначенийаргументамыможемнайтисоответствующуюточкуна линии котангенсов и ее абсциссу — котангенс. Поэтому все значения x ≠ πk входят в область определения функции у = ctg х.
Для точек единичной окружности (которые не совпадают с точками А и В) абсциссы соответствующих точек на линии котангенсов принимают все значения от –× до +×, поскольку для любого действительного числа мы можем указать соответствующую точку на оси абсцисс, а значит, и соответствующую точку Qх на оси котангенсов. Учитывая, что точка О лежит внутри окружности, а точка Qх — вне ее (или на самой окружности), получаем, что прямая ОQх имеет с окружностью хотя бы одну общую точку (на самом деле их две). Следовательно, для любого действительного числа найдется аргумент х, такой, что сtg x равен данному действительному числу. Таким образом, область значений функции y = ctg x — все действительные числа, то есть R.
Это можно записать так: E (ctgx) = R.Из приведенных рассуждений также вытекает, что наибольшего и наименьшего значений функция ctgxне имеет.
Как было показано в § 13, котангенс — нечетная функция: ctg (-x) = -ctgx, поэтому ее график симметричен относительно начала координат.
Там же было обосновано, что котангенс — периодическая функция с наименьшим положительным периодом T= : ctg (x+ ) = ctg x, поэтому через промежутки длиной п вид графика функции ctgxповторяется.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oyзначение x= 0. Но ctg0 не существует, значит, график функции y= ctg x не пересекает ось Oy.
На оси Оx значение y= 0. Поэтому необходимо найти такие значения x, при которых ctgx, то есть абсцисса соответствующей точки линии котангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D(рис. 95), то есть при
Промежутки знакопостоянства. Как было обосновано в § 13, значения функции котангенс положительны (то есть абсцисса соответствующей точки линии котангенсов положительна) в I и III четвертях (рис. 96). Тогда ctgx> 0 при всех . Учитывая период, получаем, что ctgx> 0 при всех
Значения функции котангенс отрицательны (то есть абсцисса соответствующей точки линии котангенсов отрицательна) во II и IV четвертях, таким образом, ctgx< 0 при .

Промежутки возрастания и убывания
Учитывая периодичность функции ctg x (наименьший положительный период T = ), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке (0; ). Если (0; ) (рис. 97), то при увеличении аргумента x (x2>x1) абсцисса соответствующей точки линии котангенсов уменьшается (то есть ctgx2<ctgx1), следовательно, на этом промежутке функция ctg x убывает. Учитывая периодичность функции y= ctgx, делаем вывод, что она также убывает на каждом из промежутков
Проведенное исследование позволяет построить график функции y= ctg x аналогично тому, как был построен график функции y= tg x. Но график функции у = ctg x можно получить также с помощью геометрических преобразований графика функции у = tg х. По формуле, приведенной на с. 172, , то есть Поэтому график функции у = ctg x можно получить из графика функции у = tg х параллельным переносом вдоль оси Ох на (− ) и симметричным отображением полученного графика относительно оси Ох. Получаем график, который называется котангенсоидой (рис. 98).
Число, равное отношению синуса угла α (α ≠ π/2 + πk, kЄZ) к косинусу этого угла, есть тангенс угла α, его обозначают tgα. Поскольку для каждого значения величины х, кроме x = π/2 + πk, kЄZ, установлено взаимно-однозначное соответствие со значениями у = tgx , то тем самым задана функция у = tgx .
Свойства этой функции следуют из свойств функций y = sinx и y = cosх .
Поскольку функции у = sinх и y = cosх определены при всех значениях переменной х, область определения функции у = tgx это все действительные числа, за исключением тех точек, где cosх равен нулю, т. е. за исключением точек x = π/2 + πn, nЄZ.
Область значений функции у = tgx это всех действительные числа.
Функция у = tgx является периодической с основным периодом π: tg(α + πn) = tgα для любых αЄR, nЄZ.
Функция у = tgx нечетная, поскольку для любого значения х, которое принадлежит области определения является верным равенство tg(-x) = -tgx.
График функции у = tgx пересекается с осью Ох в точках с абсциссами, определяемыми уравнением tgx = 0, значит х = πn, nЄZ. График функции у = tgx пересекает ось Оу в единственной точке с ординатой y = 0.
Значения функции у = tgx положительны для углов, расположенных в I и III четвертях, и отрицательны для углов, расположенных во II и IV четвертях:
tgx > 0 при x Є (0 + πk; π/2 + πk), kЄZ;
tgх < 0 при x Є (-π/2 + πk; 0 + πk), kЄZ.
Функция у = tgx не имеет наибольшего и наименьшего значений.
Функция у = tgx не является монотонной. Она возрастает при x Є (-π/2 + πn; π/2 + πn), nЄZ.
Функция у = tgx непрерывна и имеет производную в каждой точке области из определения.
График рассматриваемой функции у = tgx показан на рисунке. График функции тангенс это набор линий, которые симметричны относительно начала координат и имеет вертикальные асимптоты x = π/2 + πn, nЄZ.
Знаток
(314),
закрыт
13 лет назад
Марина Васильевна
Гений
(65102)
13 лет назад
Наибольшего и наименьшего значения на отрезке, функция достигает либо в точке, где производная равно нулю или не существует, либо на концах отрезка. Найдём производную. Y’=(tgX) ‘=1/(cosX)^2, производная на этом отрезке существует и нигде не обращается в ноль. Значит достаточно найти значения функции на концах отрезка и выбрать наибольшее и наименьшее. У (-П/4)=tg(-П/4)=-1, Y(П/6)=tg(П/6)=1/sqrt3. Ответ: Унаим=
У (-П/4)=-1, Унаиб=У (П/6)=1/sqrt3.
Найти наименьшее и наибольшее значение функции y = tg x на заданном промежутке : 1) на интервале (пи / 2 ; 3пи / 2) 2) на полуинтервале (3пи / 4 ; пи] 3) на отрезке [ – пи / 4 ; пи / 6] 4) на полуинтервале [пи ; 3пи / 2).
Вы зашли на страницу вопроса Найти наименьшее и наибольшее значение функции y = tg x на заданном промежутке : 1) на интервале (пи / 2 ; 3пи / 2) 2) на полуинтервале (3пи / 4 ; пи] 3) на отрезке [ – пи / 4 ; пи / 6] 4) на полуинте?, который относится к
категории Алгебра. По уровню сложности вопрос соответствует учебной
программе для учащихся 5 – 9 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.






.png)