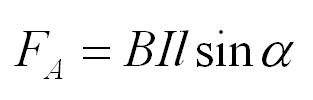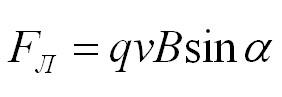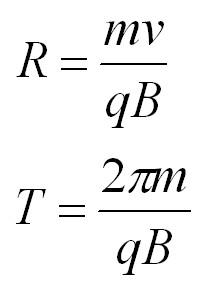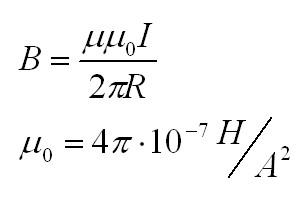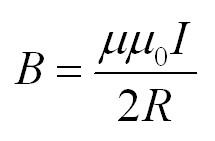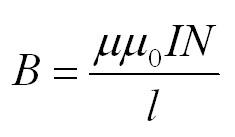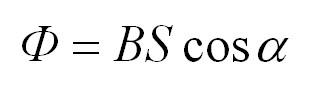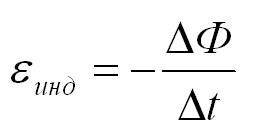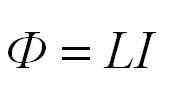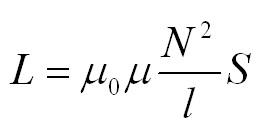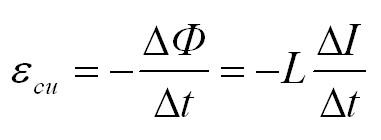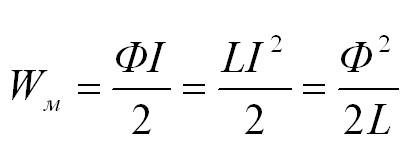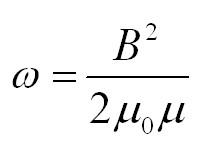Магнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между движущимися электрическими частицами.
Основные свойства магнитного поля
- Магнитное поле порождается электрическим током (движущимися зарядами).
- Магнитное поле обнаруживается по действию на электрический ток (движущиеся заряды).
- Магнитное поле существует независимо от нас, от наших знаний о нем.
Вектор магнитной индукции
Определение
Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как→B. Единица измерения — Тесла (Тл).
За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.
Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:
B=FAmaxIl
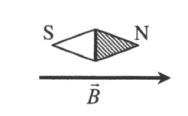
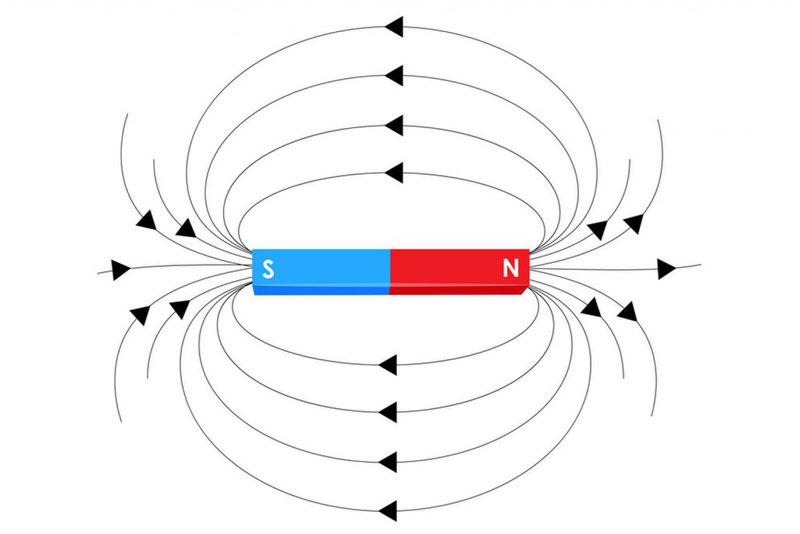
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.
Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.
Напряженность магнитного поля
Определение
Вектор напряженности магнитного поля — характеристика магнитного поля, определяющая густоту силовых линий (линий магнитной индукции). Обозначается как →H. Единица измерения — А/м.
→H=→Bμμ0
μ — магнитная проницаемость среды (у воздуха она равна 1), μ0 — магнитная постоянная, равная 4π·10−7 Гн/м.
Внимание! Направление напряженности всегда совпадает с направлением вектора магнитной индукции: →H↑↑→B.
Направление вектора магнитной индукции и способы его определения
Чтобы определить направление вектора магнитной индукции, нужно:
- Расположить в магнитном поле компас.
- Дождаться, когда магнитная стрелка займет устойчивое положение.
- Принять за направление вектора магнитной индукции направление стрелки компаса «север».
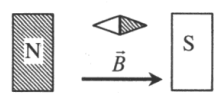
В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:
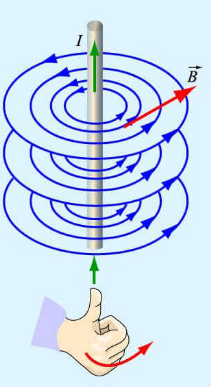
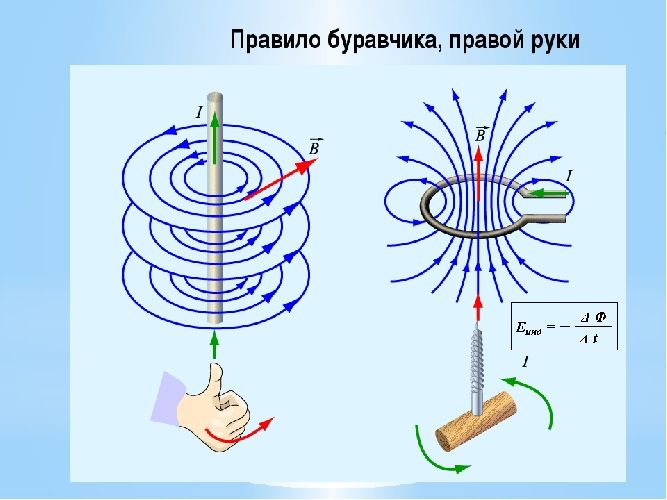
При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:
При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора →B магнитной индукции.
Отсюда следует, что:
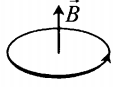
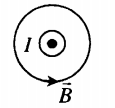
- Если по витку ток идет против часовой стрелки, то вектор магнитной индукции →B направлен вверх.
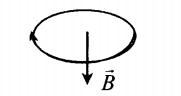
- Если по витку ток идет по часовой стрелке, то вектор магнитной индукции →B направлен вниз.
Способы обозначения направлений векторов:
| Вверх | |
| Вниз | |
| Влево | |
| Вправо | |
| На нас перпендикулярно плоскости чертежа |  |
| От нас перпендикулярно плоскости чертежа |  |
Пример №1. На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?
Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.
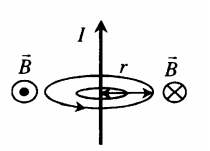
Магнитное поле прямолинейного тока
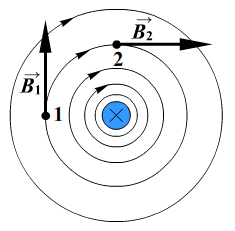
Линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. Центр окружностей совпадает с осью проводника.
Вид сверху:
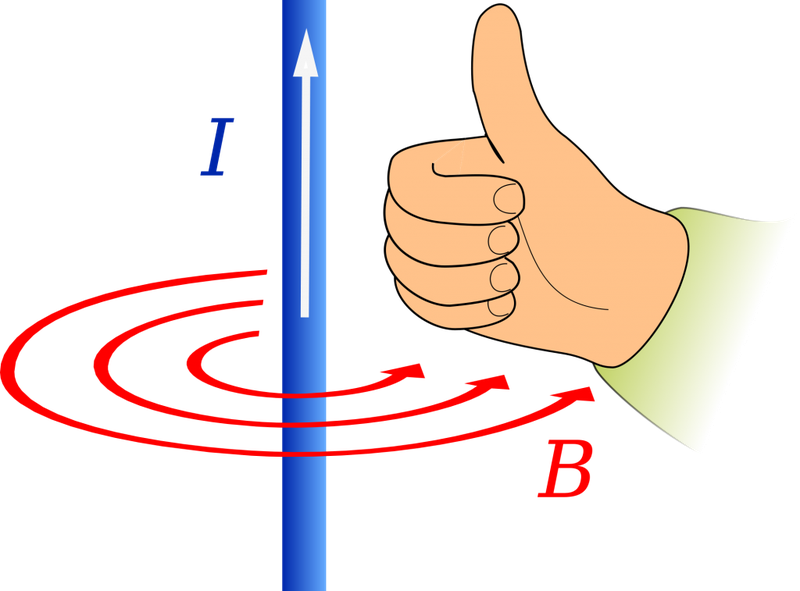
Если ток идет вверх, то силовые линии направлены против часовой стрелки. Если вниз, то они направлены по часовой стрелке. Их направление можно определить с помощью правила буравчика или правила правой руки:
Правило буравчика (правой руки)
Если большой палец правой руки, отклоненный на 90 градусов, направить в сторону тока в проводнике, то остальные 4 пальца покажут направление линий магнитной индукции.
Модуль вектора магнитной индукции на расстоянии r от оси проводника:
B=μμ0I2πr
Модуль напряженности:
H=I2πr
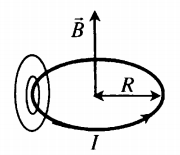
Магнитное поле кругового тока
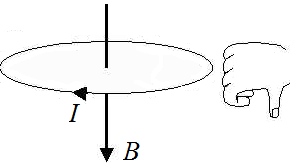
Силовые линии представляют собой окружности, опоясывающие круговой ток. Вектор магнитной индукции в центре витка направлен вверх, если ток идет против часовой стрелки, и вниз, если по часовой стрелке.
Определить направление силовых линий магнитного поля витка с током можно также с помощью правила правой руки:
Если расположить четыре пальца правой руки по направлению тока в витке, то отклоненный на 90 градусов большой палец, покажет направление вектора магнитной индукции.
Модуль вектора магнитной индукции в центре витка, радиус которого равен R:
B=μμ0I2R
Модуль напряженности в центре витка:
H=I2R
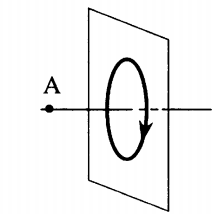
Пример №2. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?
Если мысленно обхватить виток так, чтобы четыре пальца правой руки были бы направлены в сторону тока, то отклоненный на 90 градусов большой палец правой руки показал бы, что вектор магнитной индукции в точке А направлен вправо.
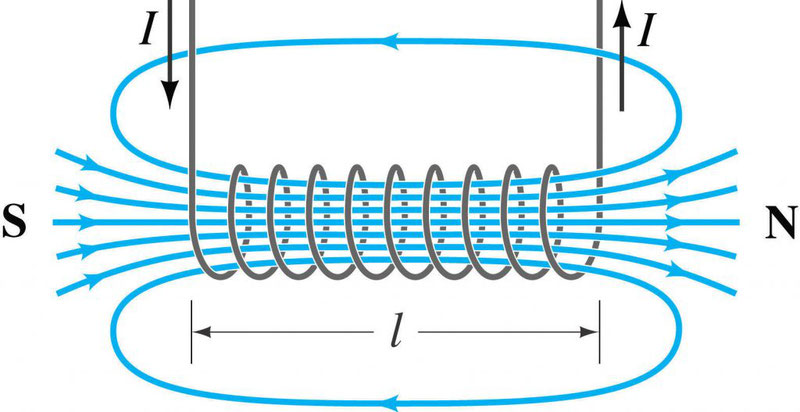
Магнитное поле электромагнита (соленоида)
Определение
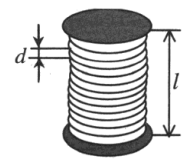
Соленоид — это катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра.
Число витков в соленоиде N определяется формулой:
N=ld
l — длина соленоида, d — диаметр проволоки.
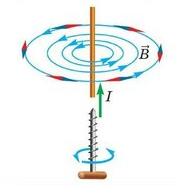
Линии магнитной индукции являются замкнутыми, причем внутри соленоида они располагаются параллельно друг другу. Поле внутри соленоида однородно.
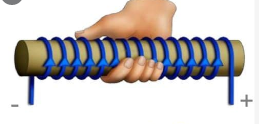
Если ток по виткам соленоида идет против часовой стрелки, то вектор магнитной индукции →B внутри соленоида направлен вверх, если по часовой стрелке, то вниз. Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.
Модуль вектора магнитной индукции в центральной области соленоида:
B=μμ0INl=μμ0Id
Модуль напряженности магнитного поля в центральной части соленоида:
H=INl=Id
Алгоритм определения полярности электромагнита
- Определить полярность источника.
- Указать на витках электромагнита условное направление тока (от «+» источника к «–»).
- Определить направление вектора магнитной индукции.
- Определить полюса электромагнита. Там, откуда выходят линии магнитной индукции, располагается северный полюс электромагнита (N, или «–». С противоположной стороны — южный (S, или «+»).
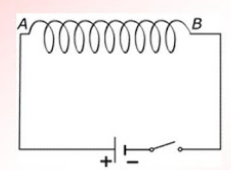
Пример №3. Через соленоид пропускают ток. Определите полюсы катушки.
Ток условно течет от положительного полюса источника тока к отрицательному. Следовательно, ток течет по виткам от точки А к точке В. Мысленно обхватив соленоид пальцами правой руки так, чтобы четыре пальца совпадали с направлением тока в витках соленоида, отставим большой палец на угол 90 градусов. Он покажет направление линий магнитной индукции внутри соленоида. Проделав это, увидим, что линии магнитной индукции направлены вправо. Следовательно, они выходят из В, который будет являться северным полюсом. Тогда А будет являться южным полюсом.
Задание EF17530
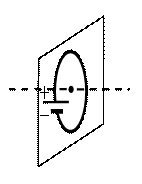
Ответ:
а) вертикально вверх в плоскости витка
б) вертикально вниз в плоскости витка
в) вправо перпендикулярно плоскости витка
г) влево перпендикулярно плоскости витка
Алгоритм решения
1.Определить правило, по которому можно определить направление вектора магнитной индукции в данном случае.
2.Применить выбранное правило и определить направление вектора магнитной индукции относительно рисунка.
Решение
По условию задачи мы имеем дело с круглым проволочным витком. Поэтому для определения вектора →B магнитной индукции мы будем использовать правило правой руки.
Чтобы применить это правило, нам нужно знать направление течение тока в проводнике. Условно ток течет от положительного полюса источника к отрицательному. Следовательно, на рисунке ток течет по витку в направлении хода часовой стрелки.
Теперь можем применить правило правой руки. Для этого мысленно направим четыре пальца правой руки в направлении тока в проволочном витке. Теперь отставим на 90 градусов большой палец. Он показывает относительно рисунка влево. Это и есть направление вектора магнитной индукции.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18109
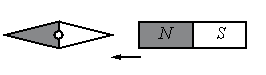
Ответ:
а) повернётся на 180°
б) повернётся на 90° по часовой стрелке
в) повернётся на 90° против часовой стрелки
г) останется в прежнем положении
Алгоритм решения
- Вспомнить, как взаимодействуют магниты.
- Определить исходное положение полюсов.
- Определить конечное положение полюсов и установить, как изменится положение магнитной стрелки.
Решение
Одноименные полюсы магнитов отталкиваются, а разноименные притягиваются. Изначально южный полюс магнитной стрелки находится справа, а северный — слева. Полосовой магнит подносят к ее южному полюсу северной стороной. Поскольку это разноименные полюса, положение магнитной стрелки не изменится.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18266
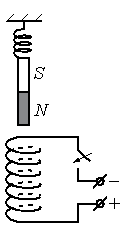
Алгоритм решения
- Определить направление тока в соленоиде.
- Определить полюса соленоида.
- Установить, как будет взаимодействовать соленоид с магнитом.
- Установить, как будет себя вести магнит после замыкания электрической цепи.
Решение
Чтобы определить направление тока в соленоиде, посмотрим на расположение полюсов источника тока. Ток условно направлен от положительного полюса к отрицательному. Следовательно, относительно рисунка ток в витках соленоида направлен по часовой стрелке.
Зная направление тока в соленоиде, можно определить его полюса. Северным будет тот полюс, из которого выходят линии магнитной индукции. Определить их направление поможет правило правой руки для соленоида. Мысленно обхватим соленоид так, чтобы направление четырех пальцев правой руки совпадало с направлением тока в витках соленоида. Теперь отставленный на 90 градусов большой палец покажет направление вектора магнитной индукции. Проделав все манипуляции, получим, что вектор магнитной индукции направлен вниз. Следовательно, внизу соленоида расположен северный полюс, а вверху — южный.
Известно, что одноименные полюса магнитов отталкиваются, а разноименные — притягиваются. Подвешенный полосовой магнит обращен к южному полюсу соленоида северным полюсом. А это значит, что при замыкании электрической цепи он будет растягивать пружину, притягиваясь к соленоиду (двигаться вниз).
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 22.5k
Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.
Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Магнетизм: определение
Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.
Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.
Магнитная индукция
Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.
Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.
Магнитная индукция – это силовая векторная характеристика магнитного поля.
Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.
Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.
Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.
Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!
Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.
Сила Ампера
Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:
Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.
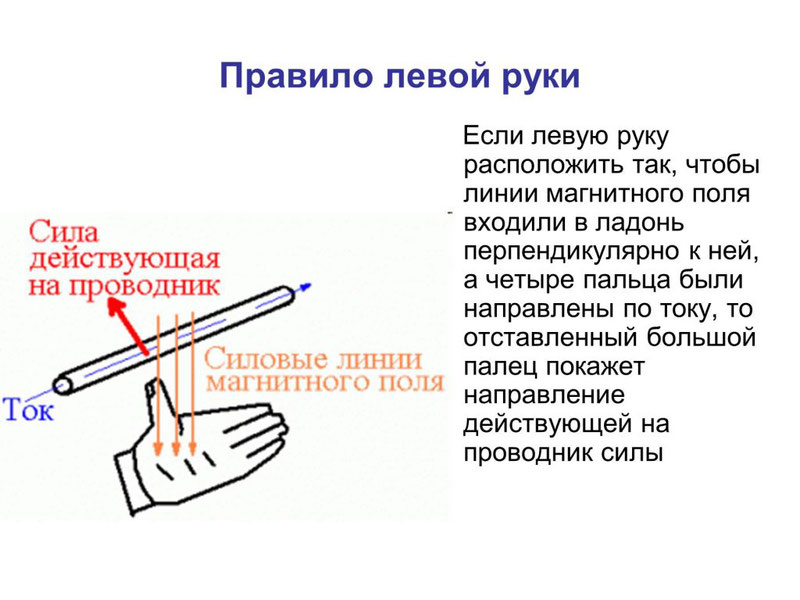
Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.
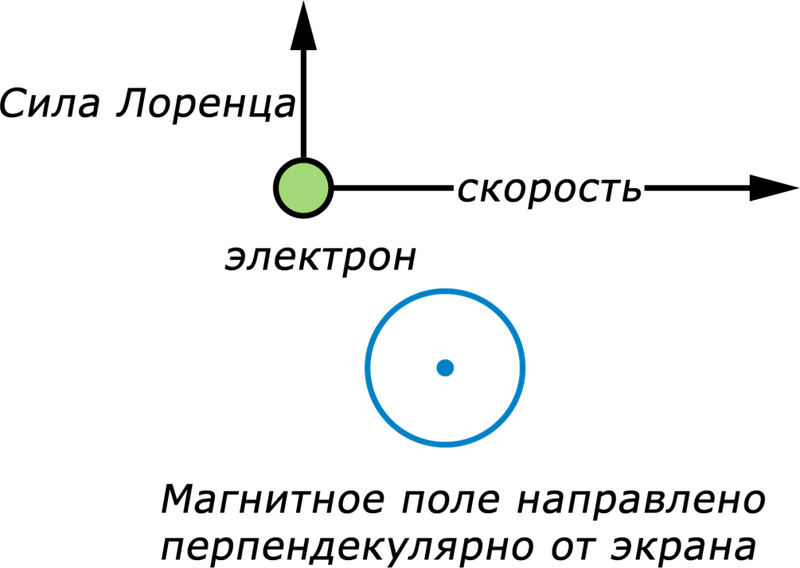
Сила Лоренца
Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.
Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
Взаимодействие токов
Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.
В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.
Во втором случае магнитная индукция в центре кругового витка с током равна:
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Магнитный поток и ЭДС
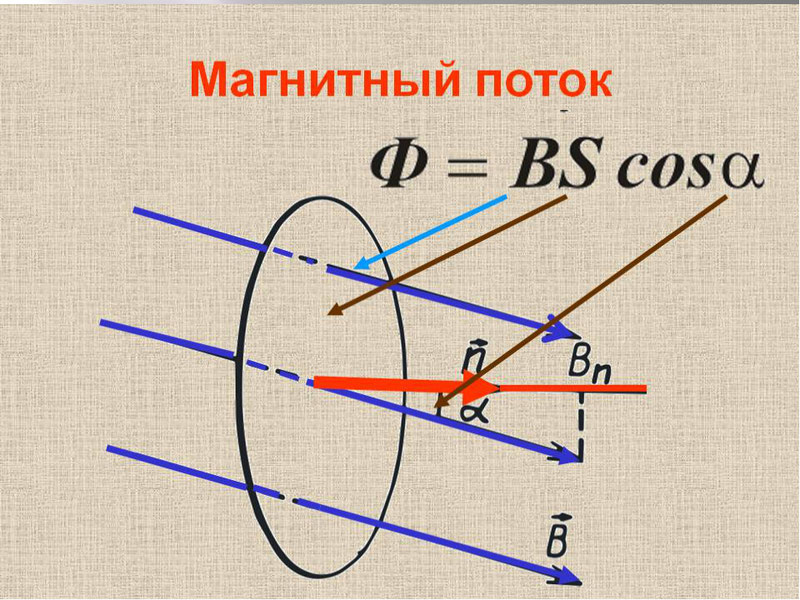
Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.
S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.
При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.
По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.
Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:
L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:
Формула для ЭДС самоиндукции:
Энергия магнитного поля
Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:
Объемная плотность энергии поля:
Конечно, это не все основные формулы раздела физики «электричество и магнетизм», однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в сервис студенческой помощи.
Свойством поля магнитного в любой его точке с позиции силы выступает вектор магнитной индукции [overrightarrow{mathrm{B}}].
Вектор индукции магнитного поля: главные понятия
Рассмотрим определение вектора индукции магнитного поля. Индукцию определяют как предел отношения F силы, воздействующий на магнитное поле, на ток [text { Idl }] к произведению элементарного тока [text { I }] со значением элемента проводника [text { dl }]. Другими словами, магнитная индукция действует по направлению перпендикулярно [perp] по направлению тока (или по-другому к элементу проводника [text { dl }Rightarrow] из (1), а также вектор магнитной индукции поля перпендикулярен [perp] к направлению силы, которая действует с магнитного поля.
Вектор магнитной индукции однородного поля и неоднородного
Если [overrightarrow{mathrm{B}}=mathrm{const}], то поле является однородным. Если оно не изменяется с течением времени, то про него говорят, что поле постоянное.
Вектор индукции магнитного поля: важные формулы
Важно!
Формула с векторами преобразуется в модульную форму, потому что векторы задают направление, а модульная форма — значения, которые необходимы для решения задачи.
Формула
Модуль вектора индукции однородного поля находят следующим образом:
[mathrm{B}=frac{mathrm{M}_{max }}{mathrm{P}_{mathrm{m}}}].
где [mathrm{M}_{max }] — вращающий момент в максимуме действует на контур с элементарным током, помещенный в магнитное поле, где в данном случае [mathrm{P}_{mathrm{m}}=mathrm{I} cdot mathrm{S}] — магнитный момент контура (S — площадь определенного контура).
Модуль вектора индукции магнитного поля: производные формулы
Есть еще формулы для определения модуля магнитной индукции. Она определяется как отношение силы в максимуме [mathrm{F}_{max }], которое реагирует на проводник длины (при этом L= 1 м) к силе элементарного тока [text { I }] в проводнике:
[B=frac{F_{max }}{I cdot L}]
В вакууме модуль индукции будет равен:
[mathrm{B}=mu 0 cdot mathrm{H}]
Чтобы найти вектор индукции через силу Лоренца, следует преобразовать формулу: [overrightarrow{mathrm{F}}=mathrm{q} cdot[overrightarrow{mathrm{V}} times overrightarrow{mathrm{B}}]] (Крестом обозначается произведение векторов)
[vec{F}=B cdot q cdot v cdot sin alpha]
[B=frac{F}{sin alpha cdot q v}]
В данном случае угол α — это угол между вектором индукции и скорости. Стоит отметить, что направление силы Лоренца [overrightarrow{mathrm{F}}] перпендикулярно [perp] каждому вектору, направлено по правилу Буравчика. Под символом q подразумевается заряд в магнитном поле.
Интересно
В СИ единицей модуля магнитной индукции принимается 1 Тесла (кратко — Тл), где [1 Tл=frac{H}{Aм}]
Как определяется направление вектора индукции магнитного поля?
За направление вектора индукции магнитного поля [overrightarrow{mathrm{B}}] используют направление, в котором устанавливается под воздействием поля утвердительного нормали к току с контору. Другими словами объясняют так: вектор идет в направление поступательного перемещения правого винта при вращении по направлению передвижения тока внутри контура.
Вектор индукции [overrightarrow{mathrm{B}}] обладает направлением, которое начинается со стрелки южного полюса [text { S }] (она свободна передвигается в поле) к полюсу северному [text { N }].
Магнитное поле возникает из-за электрических зарядов (элементарными токами), движущиеся в нем.
Для того чтобы определить направление вектора магнитной индукции в проводнике с элементарным током, используют правило правой руки (Буравчика). Они формулируются так:
- Для катушки с током: 4 согнутых пальца руки, которые обхватывают катушку, направляют по течению току. В это время оставленный большой палец на [90^{circ}] указывает на направление магнитной индукции [overrightarrow{mathrm{B}}] в середине катушки.
- Для прямого проводника с элементарным током: большой палец руки, который оставляется на [90^{circ}], направить по течению элементарного тока. В это время 4 согнутых пальца, которые держат проводник, показывают сторону, куда направлена индукция магнитного поля.
Задания по теме
Разберем примеры, в которых будет задействована данная формула и свойства.
Пример 1
Условие задачи:
Проводник представлен в квадратной форме. Каждая из сторон равна d. В данный момент по нему проходит элементарный ток силы I. Найдите индукцию магнитного поля в месте, где диагонали квадрата пересекаются.
Решение задачи следующее:
Сделаем рисунок, в котором плоскость совпадает с плоскостью проводника. Изобразим направление вектора индукции магнитного поля.
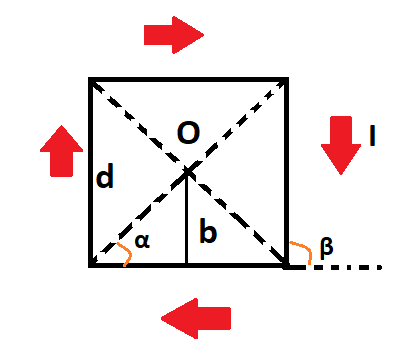
В данной точке О получаются проводники с элементарным током, которые расположены прямолинейно и вектор магнитной индукции поля перпендикулярен плоскости. Направления напряжености полей определяется в соответствием с правилом правого винта,то есть перпендикулярны плоскости изображения. Поэтому сумму векторов по принципу суперпозиции надо заменить на алгебраический вид. Получим следующее выражение: B=B1+B2+B3+B4
Из симметричности рисунка можно увидеть, что модули вектора индукции магнитного поля одинаковы. Получаем следующее: B=4B1
В разделе физике «Электромагнетизм» использовали одну из формул, чтобы рассчитать модуль индукции прямолинейного проводника с элементарным током.
Чтобы формула подошла к данной задачи, ее применяют в следующем виде:
[mathrm{B}_{1}=frac{mathrm{I} cdot mu_{0}}{4 mathrm{pi b}}(cos alpha-cos beta)]
углы α и β, которые отмечены на рисунке:
[beta=pi-alpha rightarrow cos beta=cos (pi-alpha)=-cos alpha]
Используем формулу [B_{1}=frac{I cdot mu_{0}}{4 pi b}(cos alpha-cos beta)] и преобразуем с применением тригонометрического свойства:
[mathrm{B}_{1}=frac{mathrm{I} cdot mu_{0}}{2 mathrm{pi b}} cdot cos alpha]
Поскольку у нас квадратная форма, то следует заметить следующее:
[mathrm{b}=mathrm{d} 2, alpha=frac{pi}{4} rightarrow cos alpha=frac{sqrt{2}}{2}]
Возьмем выведенные формулы и получим конечное выражение, то есть:
[mathrm{B}=4 cdot frac{mathrm{I} cdot mu_{0}}{pi mathrm{d}} cdot frac{sqrt{2}}{2}=frac{2 sqrt{2}}{pi mathrm{d}} cdot mathrm{I} cdot mu_{0}]
Ответ: [mathrm{B}=frac{2 sqrt{2}}{pi mathrm{d}} cdot mathrm{I} cdot mu_{0}]
Нет времени решать самому?
Наши эксперты помогут!
Пример 2
Условие задачи:
Бесконечно проводник с элементарным током (I) согнут под 90 градусов, который изображен на рисунке. Найдите вектор магнитной индукции однородного поля в точке А.
Решение задачи:
В точке А получается из двух частей проводника, то есть:
[overrightarrow{mathrm{B}}=mathrm{B}_{mathrm{II}}+mathrm{B}_{perp}]
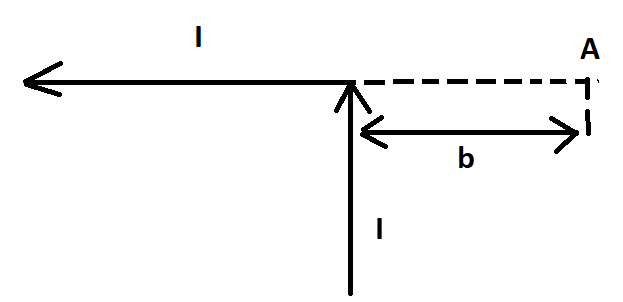
Теперь посмотрим горизонтальный участок, где расположена точка А. Данная область проводника с элементарным током формирует поле в этой точке. Вектор индукции магнитного поля [mathrm{B}_{mathrm{II}}] равен нулю, потому что в А все углы между с радиус-векторами и с элементарным током равны π.
Следовательно, произведение векторов [[mathrm{d} vec{ l } vec{r}]] и поток вектора индукции магнитного поля в законе Био-Савара-Лапласа будет равен нулю:
[overrightarrow{mathrm{B}}=frac{mu_{0}}{4 pi} oint frac{mathrm{I}[mathrm{d} vec{l} vec{r}]}{mathrm{r}^{3}}]
В этом случае [vec{r}] — радиус-вектор, который идет от элемента [mathrm{Idvec{l}}] к точке А, в которой находится индукция магнитного поля [overrightarrow{mathrm{B}}].
Индукция бесконечного проводника в точке А была бы равна:
[mathrm{B}^{prime}=frac{mu_{0}}{2 pi} frac{mathrm{I}}{mathrm{b}}]
Но так как полу бесконечный проводник, то следуя из принципа суперпозиции, получается следующее выражение для проводника магнитной индукций равна:
[mathrm{B}=mathrm{B}_{perp}=frac{1}{2} mathrm{~B}^{prime}=frac{mu_{0}}{Pi} frac{mathrm{I}}{mathrm{b}}]
Ответ: [mathrm{B}=frac{mu_{0}}{pi} frac{mathrm{I}}{mathrm{b}}]
Магнитное поле и его характеристики
теория по физике 🧲 магнетизм
Магнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между движущимися электрическими частицами.
Основные свойства магнитного поля
- Магнитное поле порождается электрическим током (движущимися зарядами).
- Магнитное поле обнаруживается по действию на электрический ток (движущиеся заряды).
- Магнитное поле существует независимо от нас, от наших знаний о нем.
Вектор магнитной индукции
Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как → B . Единица измерения — Тесла (Тл).
За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.
Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:
B = F A m a x I l . .
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.
Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.
Напряженность магнитного поля
Вектор напряженности магнитного поля — характеристика магнитного поля, определяющая густоту силовых линий (линий магнитной индукции). Обозначается как → H . Единица измерения — А/м.
μ — магнитная проницаемость среды (у воздуха она равна 1), μ 0 — магнитная постоянная, равная 4 π · 10 − 7 Гн/м.
Внимание! Направление напряженности всегда совпадает с направлением вектора магнитной индукции: → H ↑↑ → B .
Направление вектора магнитной индукции и способы его определения
Чтобы определить направление вектора магнитной индукции, нужно:
- Расположить в магнитном поле компас.
- Дождаться, когда магнитная стрелка займет устойчивое положение.
- Принять за направление вектора магнитной индукции направление стрелки компаса «север».
В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:
При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:
При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора → B магнитной индукции.
Отсюда следует, что:
- Если по витку ток идет против часовой стрелки, то вектор магнитной индукции → B направлен вверх.
- Если по витку ток идет по часовой стрелке, то вектор магнитной индукции → B направлен вниз.
Способы обозначения направлений векторов:
| Вверх |  |
| Вниз |  |
| Влево |  |
| Вправо |  |
| На нас перпендикулярно плоскости чертежа |  |
| От нас перпендикулярно плоскости чертежа |  |
Пример №1. На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?
Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.
Магнитное поле прямолинейного тока
Линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. Центр окружностей совпадает с осью проводника.
Если ток идет вверх, то силовые линии направлены против часовой стрелки. Если вниз, то они направлены по часовой стрелке. Их направление можно определить с помощью правила буравчика или правила правой руки:
Правило буравчика (правой руки)
Если большой палец правой руки, отклоненный на 90 градусов, направить в сторону тока в проводнике, то остальные 4 пальца покажут направление линий магнитной индукции.
Модуль вектора магнитной индукции на расстоянии r от оси проводника:
B = μ μ 0 I 2 π r . .
Магнитное поле кругового тока
Силовые линии представляют собой окружности, опоясывающие круговой ток. Вектор магнитной индукции в центре витка направлен вверх, если ток идет против часовой стрелки, и вниз, если по часовой стрелке.
Определить направление силовых линий магнитного поля витка с током можно также с помощью правила правой руки:
Если расположить четыре пальца правой руки по направлению тока в витке, то отклоненный на 90 градусов большой палец, покажет направление вектора магнитной индукции.
Модуль вектора магнитной индукции в центре витка, радиус которого равен R:
Модуль напряженности в центре витка:
Пример №2. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?
Если мысленно обхватить виток так, чтобы четыре пальца правой руки были бы направлены в сторону тока, то отклоненный на 90 градусов большой палец правой руки показал бы, что вектор магнитной индукции в точке А направлен вправо.
Магнитное поле электромагнита (соленоида)
Соленоид — это катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра.
Число витков в соленоиде N определяется формулой:
l — длина соленоида, d — диаметр проволоки.
Линии магнитной индукции являются замкнутыми, причем внутри соленоида они располагаются параллельно друг другу. Поле внутри соленоида однородно.
Если ток по виткам соленоида идет против часовой стрелки, то вектор магнитной индукции → B внутри соленоида направлен вверх, если по часовой стрелке, то вниз. Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.
Модуль вектора магнитной индукции в центральной области соленоида:
B = μ μ 0 I N l . . = μ μ 0 I d . .
Модуль напряженности магнитного поля в центральной части соленоида:
H = I N l . . = I d . .
Алгоритм определения полярности электромагнита
- Определить полярность источника.
- Указать на витках электромагнита условное направление тока (от «+» источника к «–»).
- Определить направление вектора магнитной индукции.
- Определить полюса электромагнита. Там, откуда выходят линии магнитной индукции, располагается северный полюс электромагнита (N, или «–». С противоположной стороны — южный (S, или «+»).
Пример №3. Через соленоид пропускают ток. Определите полюсы катушки.
Ток условно течет от положительного полюса источника тока к отрицательному. Следовательно, ток течет по виткам от точки А к точке В. Мысленно обхватив соленоид пальцами правой руки так, чтобы четыре пальца совпадали с направлением тока в витках соленоида, отставим большой палец на угол 90 градусов. Он покажет направление линий магнитной индукции внутри соленоида. Проделав это, увидим, что линии магнитной индукции направлены вправо. Следовательно, они выходят из В, который будет являться северным полюсом. Тогда А будет являться южным полюсом.

а) вертикально вверх в плоскости витка
б) вертикально вниз в плоскости витка
в) вправо перпендикулярно плоскости витка
г) влево перпендикулярно плоскости витка
Алгоритм решения
Решение
По условию задачи мы имеем дело с круглым проволочным витком. Поэтому для определения вектора → B магнитной индукции мы будем использовать правило правой руки.
Чтобы применить это правило, нам нужно знать направление течение тока в проводнике. Условно ток течет от положительного полюса источника к отрицательному. Следовательно, на рисунке ток течет по витку в направлении хода часовой стрелки.
Теперь можем применить правило правой руки. Для этого мысленно направим четыре пальца правой руки в направлении тока в проволочном витке. Теперь отставим на 90 градусов большой палец. Он показывает относительно рисунка влево. Это и есть направление вектора магнитной индукции.
pазбирался: Алиса Никитина | обсудить разбор | оценить
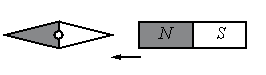
а) повернётся на 180°
б) повернётся на 90° по часовой стрелке
в) повернётся на 90° против часовой стрелки
г) останется в прежнем положении
Алгоритм решения
- Вспомнить, как взаимодействуют магниты.
- Определить исходное положение полюсов.
- Определить конечное положение полюсов и установить, как изменится положение магнитной стрелки.
Решение
Одноименные полюсы магнитов отталкиваются, а разноименные притягиваются. Изначально южный полюс магнитной стрелки находится справа, а северный — слева. Полосовой магнит подносят к ее южному полюсу северной стороной. Поскольку это разноименные полюса, положение магнитной стрелки не изменится.
pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения
- Определить направление тока в соленоиде.
- Определить полюса соленоида.
- Установить, как будет взаимодействовать соленоид с магнитом.
- Установить, как будет себя вести магнит после замыкания электрической цепи.
Решение
Чтобы определить направление тока в соленоиде, посмотрим на расположение полюсов источника тока. Ток условно направлен от положительного полюса к отрицательному. Следовательно, относительно рисунка ток в витках соленоида направлен по часовой стрелке.
Зная направление тока в соленоиде, можно определить его полюса. Северным будет тот полюс, из которого выходят линии магнитной индукции. Определить их направление поможет правило правой руки для соленоида. Мысленно обхватим соленоид так, чтобы направление четырех пальцев правой руки совпадало с направлением тока в витках соленоида. Теперь отставленный на 90 градусов большой палец покажет направление вектора магнитной индукции. Проделав все манипуляции, получим, что вектор магнитной индукции направлен вниз. Следовательно, внизу соленоида расположен северный полюс, а вверху — южный.
Известно, что одноименные полюса магнитов отталкиваются, а разноименные — притягиваются. Подвешенный полосовой магнит обращен к южному полюсу соленоида северным полюсом. А это значит, что при замыкании электрической цепи он будет растягивать пружину, притягиваясь к соленоиду (двигаться вниз).
pазбирался: Алиса Никитина | обсудить разбор | оценить
Вектор магнитной индукции: формула
Один из параметров магнитного поля – его силовая характеристика. Она обозначает, с какой силой поле влияет на движущиеся в нём заряженные частицы. Это значение из разряда векторных величин, носит название магнитная индукция B→.
Физический смысл магнитной индукции (МИ)
Возможность действовать на предмет магнитным полем (МП) определяет сущность настоящей индукции. Она появляется в момент перемещения в катушке индуктивности магнита постоянной природы. Результатом такого движения является появление тока, с одновременным увеличением магнитного потока. Поскольку обмотка у катушки металлическая, а структура металла – кристаллическая решётка, то можно объяснить физические свойства этого явления.
Электроны, находящиеся в этой решётке, при отсутствии магнитного воздействия находятся в покое. Движения никакого нет. Оно начинается в тот момент, когда электроны попадают под воздействие переменного МП (поле изменяется при перемещении постоянного магнита).
Значение возникающего в катушке тока зависит от диаметра жилы и количества витков, физических характеристик магнита и скорости его движения.
Единица размерности в системе Си рассматриваемой характеристики – тесла. Она обозначается буквами Тл.
Важно! Электроны в решётке, после попадания катушки в МП, разворачиваются под некоторым углом и выстраиваются вдоль силовых линий МП. Количество ориентированных частиц и однородность их размещения зависимы от величины поля.
Вектор – это вектор индукции магнитного поля (градиентный параметр МП).
Направление вектора МИ
Направление магнитных полей может указать стрелка магнита, помещаемая в эти поля. Она будет крутиться до тех пор, пока не остановится. Северный конец стрелки покажет, куда ориентирован B→ орт того или иного поля.
Таким же образом ведёт себя рамка с током, имеющая возможность без помех ориентироваться в МП. Направленность вектора индукции указывает ориентацию нормали к такому замкнутому электромагнитному контуру.
Внимание! Здесь используют правило буравчика (правого винта). Если винт вращать так, как направлен ток в рамке, то поступательное продвижение винта совпадёт с направлением положительной нормали.
В некоторых случаях, чтобы найти направление, применяют правило правой руки.
Наглядное отображение линий МИ
Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.
Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.
С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.
Модуль вектора магнитной индукции
Чтобы определить величину вектора МИ, нужно узнать его модуль. Как определяется модуль вектора магнитной индукции (градиент)? Это можно понять на примере небольшой модели. Если поместить в поле подковообразного магнита горизонтально подвешенный проводник, то МП магнита будет действовать только на участок, расположенный в междуполюсном промежутке. Сила F→, действующая на этот участок, будет направлена под прямым углом к линиям индукции и самому проводнику. Она достигает своего максимума, когда орт МИ располагается перпендикулярно проводнику.
Значение модуля B→ будет равно отношению максимального значения этой силы F→ к произведению длины отрезка ∆L на силу движения зарядов (I), а именно:
Основные формулы для вычисления вектора МИ
Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.
Закон Био-Савара-Лапласа
Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.
Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.
Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB:
dB = µ0 *I*dl*sin α /4*π*r2,
где:
- dB – магнитная индукция, Тл;
- µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
- I – сила тока, А;
- dl – отрезок проводника, м;
- r – расстояние до точки нахождения магнитной индукции, м;
- α – угол, образованный r и вектором dl.
Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме.
Существуют формулы, описывающие этот закон для отдельных случаев МП:
- поля прямого перемещения электронов;
- поля кругового движения заряженных частиц.
Формула для МП первого типа имеет вид:
Для кругового движения она выглядит так:
В этих формулах µ – это магнитная проницаемость среды (относительная).
Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.
Принцип суперпозиции
Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:
Теорема о циркуляции
Изначально в 1826 году Андре Ампер сформулировал данную теорему. Он разобрал случай с постоянными электрическими полями, его теорема применима к магнитостатике. Теорема гласит: циркуляция МП постоянного электричества по любому контуру соразмерна сумме сил всех токов, которые пронизывают этот контур.
Стоит знать! Тридцать пять лет спустя Д. Максвелл обобщил это утверждение, проведя параллели с гидродинамикой.
Другое название теоремы – закон Ампера, описывающий циркуляцию МП.
Математически теорема записывается следующим образом.
где:
- B→– вектор магнитной индукции;
- j→ – плотность движения электронов.
Это интегральная форма записи теоремы. Здесь в левой части интегрируют по некоторому замкнутому контуру, в правой части – по натянутой поверхности на полученный контур.
Магнитный поток
Одна из физических величин, характеризующих уровень МП, пересекающего любую поверхность, – магнитный поток. Обозначается буквой φ и имеет единицу измерения вебер (Вб). Эта единица характерна для системы СИ. В СГС магнитный поток измеряется в максвеллах (Мкс):
Магнитный поток φ определяет величину МП, пронизывающую определённую поверхность. Поток φ зависит от угла, под которым поле пронизывает поверхность, и силы поля.
Формула для расчёта имеет вид:
где:
- В – скалярная величина градиента магнитной индукции;
- S – площадь пересекаемой поверхности;
- α – угол, образованный потоком Ф и перпендикуляром к поверхности (нормалью).
Внимание! Поток Ф будет наибольшим, когда B→ совпадёт с нормалью по направлению (угол α = 00). Аналогично Ф = 0, когда он проходит параллельно нормали (угол α = 900).
Вектор магнитной индукции, или магнитная индукция, указывает направление поля. Применяя простые методы: правило буравчика, свободно ориентирующуюся магнитную стрелку или контур с током в магнитном поле, можно определить направление действия этого поля.
Видео
Магнитная индукция, магнитный поток: определение, формулы, смысл
Физический смысл магнитной индукции
Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся.
Васильев Дмитрий ПетровичПрофессор электротехники СПбГПУ Если же металл попадает под действие переменного магнитного поля (из-за перемещения постоянного магнита внутри катушки – именно перемещения), то заряды начинают двигаться под действием этого магнитного поля.
В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.
При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.
Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.
Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.
Формула магнитной индукции
где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.
Формула магнитной индукции:
Формула магнитной индукции: B = Mmax/IS
- B — индукция магнитного поля (в Тл)
- Mmax — максимальный крутящий момент магнитных сил, приложенных к рамке (в Нм)
- l — длина проводника (в м)
- S — площадь рамки (в м²)
Другие формулы, где встречается B
Эти формулы также можно использовать для её расчёта.
Сила Ампера:
Сила Ампера: Fa=IBL sinα
- Fa — сила Ампера (в Н — ньютон)
- I — сила тока (в А — ампер)
- B — индукция магнитного поля (в Тл)
- L — длина проводника (в м)
- α — угол между вектором В и одним из направлений (силы тока, скорости или др.; измеряется в рад. или град.)
Сила Лоренца:
Сила Лоренца: Fл = qvB sinα
- Fл — сила Лоренца (в Н — ньютон)
- q — заряд частицы (в Кл — кулон)
- v — скорость (в м/с)
- B — индукция (в Тл)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Магнитный поток:
Магнитный поток: Ф = BS cosα
- Ф — магнитный поток (в Вб – вебер)
- B — индукция (в Тл)
- S — площадь рамки (в м²)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Магнитный поток
Магнитный поток это скалярная величина, которая характеризует действие магнитной индукции на некий металлический контур.
Магнитная индукция определяется числом силовых линий, проходящих через 1 см2 сечения металла.
Магнитометры, используемые для ее измерения, называют теслометрами.
Абрамян Евгений ПавловичДоцент кафедры электротехники СПбГПУ Единицей измерения магнитной индукции в системе СИ является Тесла (Тл).
После прекращения движение электронов в катушке сердечник, если он выполнен из мягкого железа, теряет магнитные качества. Если он изготовлен из стали, то он имеет способность некоторое время сохранять свои магнитные свойства.
Взаимодействие магнитов
Постоянный магнит (или магнитная стрелка) ориентируется вдоль магнитного меридиана Земли. Тот его конец, который указывает на север, называется северным полюсом (N), а противоположный конец — южным полюсом (S). Приближая два магнита друг к другу, заметим, что одноименные их полюсы отталкиваются, а разноименные — притягиваются (рис. 1).
Если разделить полюса, разрезав постоянный магнит на две части, то мы обнаружим, что каждая из них тоже будет иметь два полюса, т. е. будет постоянным магнитом (рис. 2). Оба полюса — северный и южный, — неотделимые друг от друга, равноправны.
Магнитное поле, создаваемое Землей или постоянными магнитами, изображается, подобно электрическому полю, магнитными силовыми линиями. Картину силовых линий магнитного поля какого-либо магнита можно получить, помещая над ним лист бумаги, на котором насыпаны равномерным слоем железные опилки. Попадая в магнитное поле, опилки намагничиваются — у каждой из них появляется северный и южный полюсы. Противоположные полюсы стремятся сблизиться друг с другом, но этому мешает трение опилок о бумагу. Если постучать по бумаге пальцем, трение уменьшится и опилки притянутся друг к другу, образуя цепочки, изображающие линии магнитного поля.
На рис. 3 показано расположение в поле прямого магнита опилок и маленьких магнитных стрелок, указывающих направление линий магнитного поля. За это направление принято направление северного полюса магнитной стрелки.
Направление вектора МИ
Направление магнитных полей может указать стрелка магнита, помещаемая в эти поля. Она будет крутиться до тех пор, пока не остановится. Северный конец стрелки покажет, куда ориентирован B→ орт того или иного поля.
Линии магнитной индукции
Таким же образом ведёт себя рамка с током, имеющая возможность без помех ориентироваться в МП. Направленность вектора индукции указывает ориентацию нормали к такому замкнутому электромагнитному контуру.
Внимание! Здесь используют правило буравчика (правого винта). Если винт вращать так, как направлен ток в рамке, то поступательное продвижение винта совпадёт с направлением положительной нормали.
В некоторых случаях, чтобы найти направление, применяют правило правой руки.
Наглядное отображение линий МИ
Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.
Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.
С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.
Основные формулы для вычисления вектора МИ
Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея) звучит так:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.
Математически его можно описать формулой:
Ɛi — ЭДС индукции [В]
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.
Закон Фарадея для контура из N витков
Ɛi — ЭДС индукции [В]
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
N — количество витков [-]
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:
Закон Ома для проводящего контура
Ɛi — ЭДС индукции [В]
I — сила индукционного тока [А]
R — сопротивление контура [Ом]
Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:
ЭДС индукции для движущегося проводника
Ɛi — ЭДС индукции [В]
B — магнитная индукция [Тл]
v — скорость проводника [м/с]
l — длина проводника [м]
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
- вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Закон Био-Савара-Лапласа
Формула ЭДС индукции
Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.
Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.
Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB:
dB = µ0 *I*dl*sin α /4*π*r2,
- dB – магнитная индукция, Тл;
- µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
- I – сила тока, А;
- dl – отрезок проводника, м;
- r – расстояние до точки нахождения магнитной индукции, м;
- α – угол, образованный r и вектором dl.
Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме.
Существуют формулы, описывающие этот закон для отдельных случаев МП:
- поля прямого перемещения электронов;
- поля кругового движения заряженных частиц.
Формула для МП первого типа имеет вид:
Для кругового движения она выглядит так:
В этих формулах µ – это магнитная проницаемость среды (относительная).
Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.
Принцип суперпозиции
Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:
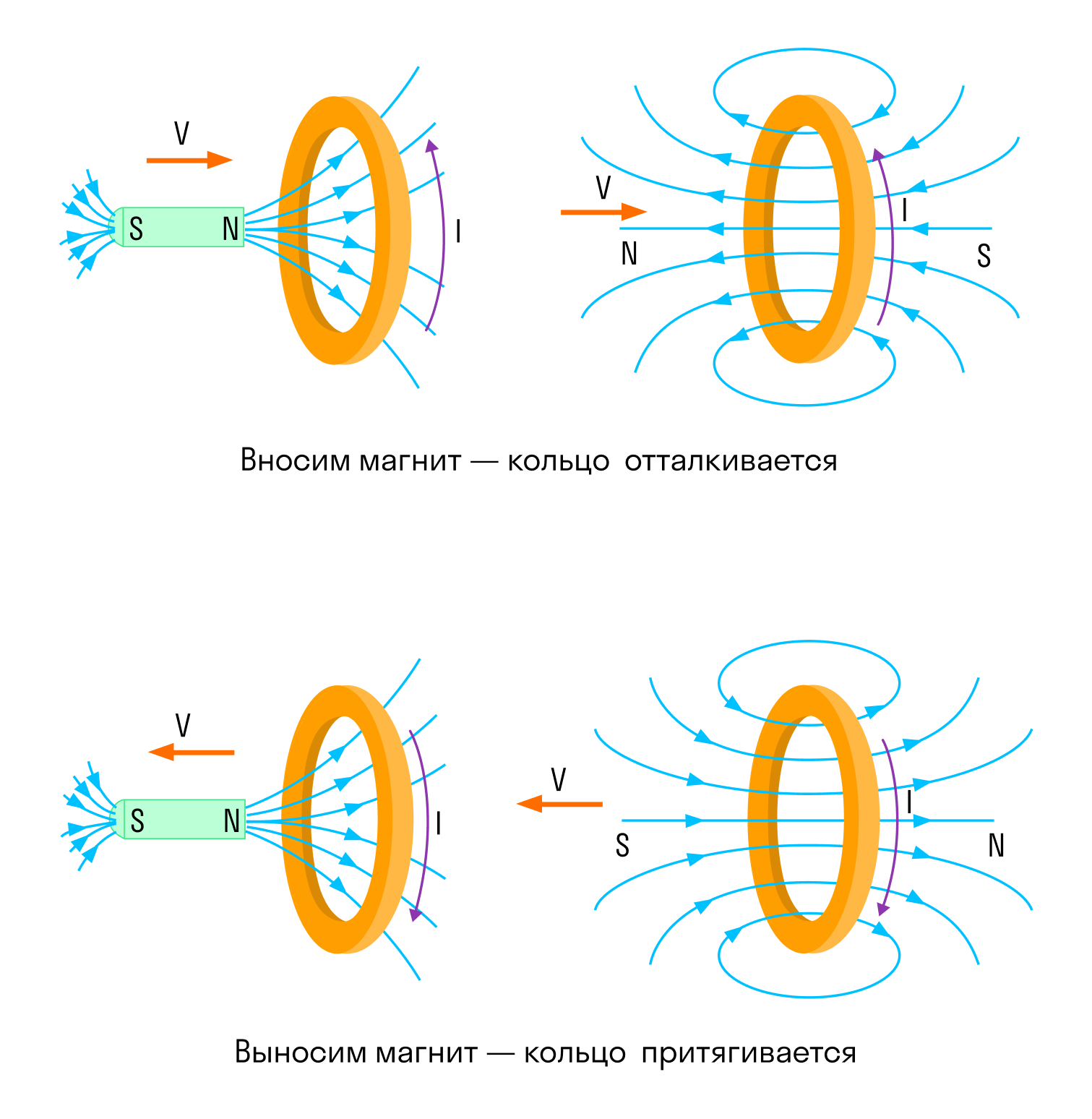
Правило Ленца
Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.
Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.
Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Майкл Фарадей провел ряд опытов, которые помогли открыть явление электромагнитной индукции.
Опыт раз. На одну непроводящую основу намотали две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
Опыт три. Катушка замкнута на гальванометр, а магнит движется вдвигается (выдвигается) относительно катушки
Вот, что показали эти опыты:
-
Индукционный ток возникает только при изменении линий магнитной индукции.
Направление тока будет различно при увеличении числа линий и при их уменьшении.
Почему возникает индукционный ток?
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС.
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
[spoiler title=”источники:”]
http://amperof.ru/teoriya/vektor-magnitnoj-indukcii-formula.html
[/spoiler]
Вектор индукции магнитного поля

4.5
Средняя оценка: 4.5
Всего получено оценок: 76.
4.5
Средняя оценка: 4.5
Всего получено оценок: 76.
Вокруг проводников с током всегда возникает вихревое магнитное поле. Его силовая характеристика называется магнитной индукцией. И, как и любая сила, магнитная индукция является векторной величиной. Рассмотрим вектор магнитной индукции более подробно.
Вектор магнитной индукции
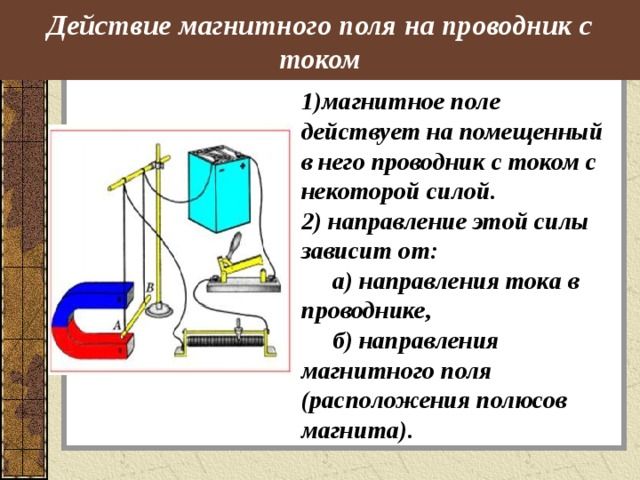
Действие магнитного поля проявляется в том, что оно влияет на проводник с током, создавая силу Ампера.
Сила Ампера зависит как от величины магнитной индукции, так и от взаимной ориентации линий магнитного поля и проводника с током. Следовательно, магнитная индукция должна характеризоваться модулем и направлением, то есть, быть векторной.
Направление индукции
Поскольку первым замеченным проявлением магнитного поля было действие на стрелку компаса, направление линий магнитного поля было принято за направление северной стрелки. Таким образом, линии, определяющие магнитный поток Земного магнитного поля, выходят из Южного полюса, тянутся вокруг земного шара, и входят в Северный полюс.
Для проводников и контуров с током были установлены специальные мнемонические правила, определяющие направление возникающего магнитного поля.
Правило буравчика: если направление поступательного движения острия буравчика при ввинчивании совпадает с направлением тока в проводнике, то направление вращательного движения буравчика в каждой точке совпадает с направлением вектора индукции магнитного поля.
Правило обхвата правой рукой для проводника с током: если большой палец правой руки указывает направление тока, то остальные пальцы будут показывать направление магнитных линий.
Правило обхвата правой рукой для катушки: если четыре пальца направляются вдоль витков катушки, в направлении тока в них, то большой палец укажет направление вектора магнитной индукции.
В правиле обхвата в обоих случаях большой палец укажет прямую линию, а остальные пальцы – охватывающую.
Приведенные правила эквивалентны. Более удобным для определения направления вектора индукции магнитного поля является правило обхвата правой рукой. Однако, в большинстве классических источников приводится правило буравчика, поэтому знать его тоже желательно.
Модуль индукции
Модуль вектора индукции магнитного поля можно получить, используя закон Ампера:
$$big|overrightarrow F big| =I{big|overrightarrow Bbig|}Δlthinspace sinthinspacealpha$$
Физический смысл магнитной индукции – это максимальная сила, которая может действовать на проводник единичной длины с единичным током.
Сила будет максимальной при условии $sin alpha = 1$. Следовательно:
$$big| B big|={big|F_{max}big|over IΔl}$$
Что мы узнали?
Магнитная индукция – это векторная величина. Ее модуль равен отношению максимальной силы, действующей со стороны поля на проводник с единичным током единичной длины, а для определения направления вектора используются мнемонические правила буравчика и обхвата правой рукой.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.5
Средняя оценка: 4.5
Всего получено оценок: 76.
А какая ваша оценка?