Как найти нижнюю кульминацию светила

Как найти нижнюю кульминацию светила

Макеты страниц

Все светила за сутки в своем видимом движении дважды пересекают небесный меридиан. Пересечение центром светила небесного меридиана называется кульминацией светила. Кульминация — слово латинское и в переводе означает вершина. Различают верхнюю и нижнюю кульминацию светила.

Рис. 1.23. Кульминация светил: а — к югу от зенита; б — к северу от зенита

В верхней кульминации высота светила наибольшая, а в нижней — наименьшая. Для незаходящих светил обе кульминации происходят над горизонтом. Для восходящих и заходящих светил верхняя кульминация происходит над горизонтом, а нижняя под горизонтом. У невосходящих светил обе кульминации происходят под горизонтом и они недоступны наблюдениям.

Верхняя кульминация светила может происходить между зенитом и точкой юга (на южной части меридиана) или между зенитом и полюсом мира (на северной части меридиана). На рис. 1.23 изображена небесная сфера. Основные круги показаны диаметрами и хордами. Из рисунка видно, что к югу от зенита кульминируют те светила, склонение которых меньше широты места, а к северу от зенита — те светила, склонение которых больше широты места.

В момент верхней кульминации часовой угол светила равен 0, а в момент нижней кульминации 180°. Азимут светила при верхней кульминации к северу от зенита равен 0, а к югу от зенита — 180°.

При кульминации светила к югу от зенита высоты в момент верхней и нижней кульминаций рассчитывают по формулам:

При кульминации светила к северу от зенита высоты в момент верхней и нижней кульминаций рассчитываются по формулам:

Обобщая формулы высоты светила для момента верхней кульминации, получаем, что . Знак плюс перед скобкой берется тогда, когда светило кульминирует к югу от зенита , а знак минус, — когда к северу от зенита .

Высота в момент нижней кульминации для всех светил определяется по единой формуле.

Формула высоты светила в момент его верхней кульминации имеет важное практическое значение. Рассчитав высоту светила в момент верхней кульминации и сравнив ее с измеренной высотой в этот же момент, можно определить поправку секстанта. По высоте светила, измеренной в момент кульминации, при знании склонения светила можно определить широту своего местонахождения. Формулы для расчета высот светил в момент верхней и нижней кульминаций позволяют установить зависимость между широтой места наблюдателя, склонением Солнца и его высотой.

Из рассмотренных формул видно, что при предельных значениях склонения Солнца, равных его высота в момент верхней кульминации на географических широтах равна 90°, т. е. Солнце будет кульминировать в зените. На географической параллели, северная широта которой равна . Солнце кульминирует в зените в день летнего солнцестояния, а на географической параллели, южная широта которой в день зимнего солнцестояния. Географическая параллель, северная широта которой равна называется северным тропиком, или тропиком Рака, а географическая параллель, южная широта которой равна южным тропиком, или тропиком Козерога. В указанных созвездиях много веков тому назад находились точки солнцестояний.

Из формул также видно, что при склонении Солнца его высота в моменты кульминаций на широтах равна нулю. На географической параллели, северная широта которой равна высота Солнца равна нулю в момент нижней кульминации в день летнего солнцестояния и в момент верхней кульминации в день зимнего солнестояния, т. е. в эти дни на этой параллели Солнце соответственно не заходит и не восходит. Эта географическая параллель называется Северным полярным кругом.

На географической параллели, южная широта которой в день зимнего солнцестояния Солнце является незаходящим светилом, а в момент летнего солнцестояния — невосходящим светилом. Эту параллель называют Южным полярным кругом.

Пример 1. Звезда Денеб; склонение звезды широта места наблюдателя Определить высоту звезды в моменты верхней и нижней кульминаций.

Решение 1. Определяем положение звезды относительно зенита в момент верхней кульминации. Так как то звезда кульминирует к северу от зенита.

2. Определяем высоту звезды в момент верхней кульминации:

3. Определяем высоту звезды в момент нижней кульминации: . Звезда Денеб на данной широте восходит и заходит, так как ее высота в моменты верхней и нижней кульминаций имеет разные знаки.

Пример 2. Дата 22 июня; склонение Солнца ; широта Ленинграда . Определить высоту Солнца в моменты верхней и нижней кульминаций.

Решение 1. Определяем положение Солнца относительно зенита в момент верхней кульминации. Так как , то Солнце кульминирует к югу от зенита.

2. Определяем высоту Солнца в момент верхней кульминации:

3. Определяем высоту Солнца в момент нижней кульминации:

Из примера видно, что на широте Ленинграда в день летнего солнцестояния Солнце опускается под горизонт не ниже Так как темнота наступает при высоте Солнца минус 6°, то в летнее время в Ленинграде почти всю ночь длятся сумерки, т. е. наблюдаются белые ночи.

Пример 3. Звезда Вега; склонение звезды широта места наблюдателя . Определить высоту звезды в моменты верхней и нижней кульминаций.

Решение. 1. Определяем положение звезды относительно зенита в момент верхней кульминации. Так как склонение звезды меньше широты места наблюдателя, то звезда кульминирует к югу от зенита.

2. Определяем высоту звезды в момент верхней кульминации: .

3. Определяем высоту звезды в момент нижней кульминации: .

Звезда Вега на данной широте является незаходящей, так как ее высота в моменты верхней и нижней кульминаций положительная.

1

Оглавление

  • ОТ АВТОРА
  • Глава I. СИСТЕМЫ НЕБЕСНЫХ КООРДИНАТ
  • 1. НЕБЕСНАЯ СФЕРА, ЕЕ ОСНОВНЫЕ ТОЧКИ, ЛИНИИ И КРУГИ
  • 2. СИСТЕМЫ НЕБЕСНЫХ КООРДИНАТ
  • 3. ЗАВИСИМОСТЬ МЕЖДУ ВЫСОТОЙ ПОЛЮСА МИРА И ГЕОГРАФИЧЕСКОЙ ШИРОТОЙ
  • 4. ГРАФИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ НЕБЕСНЫХ КООРДИНАТ
  • 5. ПАРАЛЛАКТИЧЕСКИЙ ТРЕУГОЛЬНИК И ЕГО РЕШЕНИЕ
  • 6. ВИДИМОЕ ДВИЖЕНИЕ СВЕТИЛ
  • 7. СОБСТВЕННЫЕ ДВИЖЕНИЯ ЗВЕЗД
  • 8. ВИДИМОЕ СУТОЧНОЕ ДВИЖЕНИЕ СВЕТИЛ
  • 9. УСЛОВИЯ ВОСХОДА И ЗАХОДА СВЕТИЛ
  • 10. КУЛЬМИНАЦИЯ СВЕТИЛ
  • Глава II. ЗВЕЗДНОЕ НЕБО И ХАРАКТЕРИСТИКА НАВИГАЦИОННЫХ СВЕТИЛ
  • 1. НАВИГАЦИОННЫЕ СВЕТИЛА
  • 2. ЗВЕЗДНАЯ ВЕЛИЧИНА СВЕТИЛА
  • 3. ПРАВИЛА ОТЫСКАНИЯ НАВИГАЦИОННЫХ ЗВЕЗД И ПЛАНЕТ
  • Глава III. ИЗМЕРЕНИЕ ВРЕМЕНИ
  • 1. ОСНОВЫ ИЗМЕРЕНИЯ ВРЕМЕНИ
  • 2. ЗВЕЗДНОЕ ВРЕМЯ
  • 3. ИСТИННОЕ СОЛНЕЧНОЕ ВРЕМЯ
  • 4. СРЕДНЕЕ СОЛНЕЧНОЕ ВРЕМЯ
  • 5. УРАВНЕНИЕ ВРЕМЕНИ
  • 6. СИСТЕМЫ СЧИСЛЕНИЯ ВРЕМЕНИ
  • 7. МЕСТНОЕ ВРЕМЯ
  • 8. ГРИНВИЧСКОЕ ВРЕМЯ
  • 9. ПОЯСНОЕ ВРЕМЯ
  • 10. КАРТА ЧАСОВЫХ ПОЯСОВ
  • 11. ДЕКРЕТНОЕ ВРЕМЯ
  • 12. МОСКОВСКОЕ ВРЕМЯ
  • 13. ЗАВИСИМОСТЬ МЕЖДУ ВРЕМЕНАМИ
  • 14. ЛИНИЯ СМЕНЫ ДАТ
  • Глава IV. РАСЧЕТ УСЛОВИЙ ЕСТЕСТВЕННОГО ОСВЕЩЕНИЯ И КООРДИНАТ НАВИГАЦИОННЫХ СВЕТИЛ
  • 1. УСЛОВИЯ ЕСТЕСТВЕННОГО ОСВЕЩЕНИЯ
  • 2. ОПРЕДЕЛЕНИЕ МОМЕНТОВ ЕСТЕСТВЕННОГО ОСВЕЩЕНИЯ
  • 3. АВИАЦИОННЫЙ АСТРОНОМИЧЕСКИЙ ЕЖЕГОДНИК И ПОЛЬЗОВАНИЕ ИМ ПРИ ОПРЕДЕЛЕНИИ ЭКВАТОРИАЛЬНЫХ КООРДИНАТ НАВИГАЦИОННЫХ СВЕТИЛ
  • 4. УПРОЩЕННЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ ЭКВАТОРИАЛЬНЫХ КООРДИНАТ СОЛНЦА
  • 5. УПРОЩЕННЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ ЗВЕЗДНОГО ВРЕМЕНИ
  • 6. РАСЧЕТ АЗИМУТА СОЛНЦА
  • Глава V. ПРИМЕНЕНИЕ АСТРОНОМИЧЕСКИХ КОМПАСОВ
  • 1. ПРИНЦИП ОПРЕДЕЛЕНИЯ КУРСА САМОЛЕТА С ПОМОЩЬЮ АСТРОНОМИЧЕСКИХ КОМПАСОВ
  • 2. ДИСТАНЦИОННЫЙ АСТРОНОМИЧЕСКИЙ КОМПАС ДАК-ДБ-5
  • 3. КОМПЛЕКТ И НАЗНАЧЕНИЕ ОСНОВНЫХ ЧАСТЕЙ АСТРОКОМПАСА ДАК-ДБ-5
  • 4. ПРОВЕРКА АСТРОКОМПАСА ДАК-ДБ-5 ПЕРЕД ПОЛЕТОМ
  • 5. ИСПОЛЬЗОВАНИЕ АСТРОКОМПАСА ДАК-ДБ-5
  • 6. АСТРОНОМИЧЕСКИЙ КОМПАС АК-53П
  • 7. ИСПОЛЬЗОВАНИЕ АСТРОКОМПАСА АК-53П
  • 8. ОСОБЕННОСТИ ПРИМЕНЕНИЯ АСТРОКОМПАСОВ В ЮЖНОМ ПОЛУШАРИИ
  • Глава VI. ПРИМЕНЕНИЕ СЕКСТАНТОВ
  • 1. СЕКСТАНТ ИМС-3
  • 2. УСТРОЙСТВО СЕКСТАНТА ИМС-3
  • 3. ПРЕДПОЛЕТНАЯ ПРОВЕРКА И ПОДГОТОВКА СЕКСТАНТА ИМС-3 К РАБОТЕ
  • 4. ИЗМЕРЕНИЕ ВЫСОТ СВЕТИЛ СЕКСТАНТОМ ИМС-3
  • 5. СЕКСТАНТ ИАС-1М
  • 6. СЕКСТАНТ СП-1М
  • 7. УСТРОЙСТВО СЕКСТАНТА СП-1М
  • 8. ПРЕДПОЛЕТНАЯ ПОДГОТОВКА СЕКСТАНТА СП-1М
  • 9. ИЗМЕРЕНИЯ СЕКСТАНТОМ СП-1М
  • 10. АВИАЦИОННЫЙ ПЕРИСКОПИЧЕСКИЙ СЕКСТАНТ
  • Глава VII. ОПРЕДЕЛЕНИЕ АСТРОНОМИЧЕСКИХ ЛИНИЙ ПОЛОЖЕНИЯ И МЕСТА САМОЛЕТА ПО НЕБЕСНЫМ СВЕТИЛАМ
  • 1. ГЕОГРАФИЧЕСКОЕ МЕСТО СВЕТИЛА
  • 2. КРУГ РАВНЫХ ВЫСОТ СВЕТИЛА
  • 3. ГРАФИЧЕСКИЙ СПОСОБ ПРОКЛАДКИ АЛП НА КАРТЕ
  • 4. РАСЧЕТНЫЕ ТАБЛИЦЫ ГОРИЗОНТАЛЬНЫХ КООРДИНАТ НЕБЕСНЫХ СВЕТИЛ И ПОЛЬЗОВАНИЕ ИМИ
  • 5. ПОПРАВКИ К ИЗМЕРЕННОЙ ВЫСОТЕ СВЕТИЛА
  • 6. РАСЧЕТ АСТРОНОМИЧЕСКИХ ЛИНИЙ ПОЛОЖЕНИЯ И ПРОКЛАДКА ИХ НА КАРТЕ
  • 7. РАСЧЕТ И ПРОКЛАДКА АЛП В ПОЛЯРНЫХ РАЙОНАХ И ЮЖНОМ ПОЛУШАРИИ ЗЕМЛИ
  • 8. ОПРЕДЕЛЕНИЕ МЕСТА САМОЛЕТА ПО НЕБЕСНЫМ СВЕТИЛАМ
  • 9. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ МЕСТА САМОЛЕТА ПО НЕБЕСНЫМ СВЕТИЛАМ
  • 10. ЗВЕЗДНО-СОЛНЕЧНЫЙ ОРИЕНТАТОР БЦ-63А
  • 11. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ ДЛЯ САМОЛЕТОВОЖДЕНИЯ
  • Глава VIII. ПОДГОТОВКА К ПОЛЕТУ С ИСПОЛЬЗОВАНИЕМ АСТРОНОМИЧЕСКИХ СРЕДСТВ
  • 1. ОСОБЕННОСТИ ПОДГОТОВКИ К ПОЛЕТУ С ИСПОЛЬЗОВАНИЕМ АСТРОНОМИЧЕСКИХ СРЕДСТВ
  • 2. ОПРЕДЕЛЕНИЕ ПОПРАВКИ ЧАСОВ
  • 3. ОПРЕДЕЛЕНИЕ ПОПРАВКИ СЕКСТАНТА
  • 4. ПОДГОТОВКА БОРТОВОЙ КАРТЫ И РАСЧЕТНЫХ ПОСОБИЙ
  • 5. ВЫБОР НЕБЕСНЫХ СВЕТИЛ И ОПРЕДЕЛЕНИЕ УСЛОВИЙ ЕСТЕСТВЕННОГО ОСВЕЩЕНИЯ
  • 6. ВЫПОЛНЕНИЕ АСТРОНОМИЧЕСКИХ ПРЕДВЫЧИСЛЕНИЙ
  • 7. ПРЕДПОЛЕТНАЯ ПОДГОТОВКА АСТРОНОМИЧЕСКИХ ПРИБОРОВ
Источник

УЧЕБНАЯ ДИСЦИПЛИНА: АСТРОНОМИЯ

Тема: Кульминация светил

Задание №1

Ознакомьтесь с
лекционным материалом по теме

Задание №2

Ответить на
вопросы теста:

1. Как называется момент пересечения светилом небесного
меридиана?

  1. Высотой светила
  2. Кульминацией светила
  3. Максимумом светила

2. Сколько раз при своём суточном движении светила
пересекают небесный меридиан?

  1. Один
  2. Два
  3. Три

3. Что представляет собой угол MOS, если светило
кульминирует к югу от горизонта?

  1. Сумму Q₁OS
    и MOQ    ₁
  2. Разницу Q₁OS
    и MOQ    ₁
  3. Разницу NS и MOQ₁

4. Что нужно знать, чтобы определить географическую
широту места наблюдения?

  1. Кульминацию светила
  2. Склонение светила и высоту в кульминации
  3. Склонение светила

5. Чему будет равняться высота полюса мира над
горизонтом, если мы находимся в северных широтах?

  1. φ
  2. δ
  3. М

Лекция

При своем суточном
вращении вокруг оси мира светила два раза за сутки пересекают небесный
меридиан. Явление прохождения светилом небесного меридиана называется кульминацией.

Различают верхнюю
и нижнюю кульминации. В верхней кульминации светило при
суточном движении находится в наивысшей точке над горизонтом, ближайшей к
зениту. Точка нижней кульминации светила более удалена от
точки зенита, чем точка верхней кульминации, и нижняя кульминация происходит
через половину суток после верхней кульминации.

Точка пересечения
суточной параллели светила с восточной частью истинного горизонта
называется точкой восхода светила, а точка пересечения с западной
частью истинного горизонта — точкой захода светила.

Незаходящие звезды
видны в верхней (M2M2, M3M3) и нижней (M′2M2′, M′3M3′) кульминациях.
У восходящих и заходящих звезд нижняя кульминация (M′1M1′) проходит под
горизонтом. У невосходящих звезд обе кульминации M4M4,
и M′4M4′ невидимы, т. е. происходят под горизонтом.

Найдем зависимость
между географическими и небесными координатами.

Так как кульминация светил происходит при
пересечении небесного меридиана, то плоскость совпадает с плоскостью небесного
меридиана. Суточные пути звезд изображаются отрезками, параллельными небесному
экватору QQ′QQ′. Пусть восходящая и заходящая звезда находится в верхней
кульминации M1M1. Высота полюса мира равна географической
широте φφ. ∠QOS∠QOS равен 90°−φ90°−φ и
представляет собой наклон небесного экватора к плоскости горизонта.
Дуга M1SM1S (или ∠M1OS∠M1OS) — это высота
светила над горизонтом. Эта дуга состоит из сумм двух
дуг: M1S=SQ+QM1M1S=SQ+QM1. Учитывая, что дуга SQSQ, опирающаяся
на ∠QOS∠QOS,
определяется величиной 90°−φ90°−φ, а дуга QM1QM1 обозначает
угловое расстояние звезды от небесного экватора и определяется величиной
склонения δδ, получим формулу для определения высоты звезды в ее верхней
кульминации:

hВ=(90°−φ)+δ.hВ=(90°−φ)+δ.

Для незаходящей
звезды нижняя кульминация M2′M2′ измеряется
дугой M2′NM2′N или соответствующим центральным углом (∠M2′ON∠M2′ON).
Указанный угол равен разности ∠M2′OQ′∠M2′OQ′ и ∠NOQ′∠NOQ′,
где ∠M2′OQ=δ∠M2′OQ=δ —
угловое расстояние светила от небесного экватора, а ∠NOQ′=90°−φ∠NOQ′=90°−φ —
наклон небесного экватора к плоскости горизонта. Значит, высота звезды в нижней
кульминации равна:

hН=δ−(90°−φ).hН=δ−(90°−φ).

Если обе
кульминации незаходящей звезды находятся по одну сторону от зенита
(например, M3M3 и M3′M3′), то ее верхняя кульминация
определяется из соотношения: hВ=180°−[(90°−φ)+δ]hВ=180°−[(90°−φ)+δ],
или после упрощения:

hB=90°+φ−δ.hB=90°+φ−δ.

Соотношения hВ=(90°−φ)+δhВ=(90°−φ)+δ, hН=δ−(90°−φ)hН=δ−(90°−φ) и hB=90°+φ−δhB=90°+φ−δ связывают
географическую широту с высотой и склонением звезд во время их кульминации.
Отметим, что азимуты звезд в верхней
кульминации M1M1 и M2M2 равны 0°, а азимуты звезд в нижней
кульминации M1′M1′ и M2′M2′ равны 180°. Азимуты
звезды M3M3 в верхней и нижней кульминациях равны 180°.

Источник

Что такое кульминация звёзд

Как оказалось, не все знают, что такое кульминация звёзд. По определению, кульминация означает наиболее высокий момент чего-либо. Собственно говоря, в астрономии под этим подразумевают наивысший момент движения космического объекта.

Итак, кульминация звезды — это момент её прохождения сквозь небесный меридиан во время суточного движения светила.

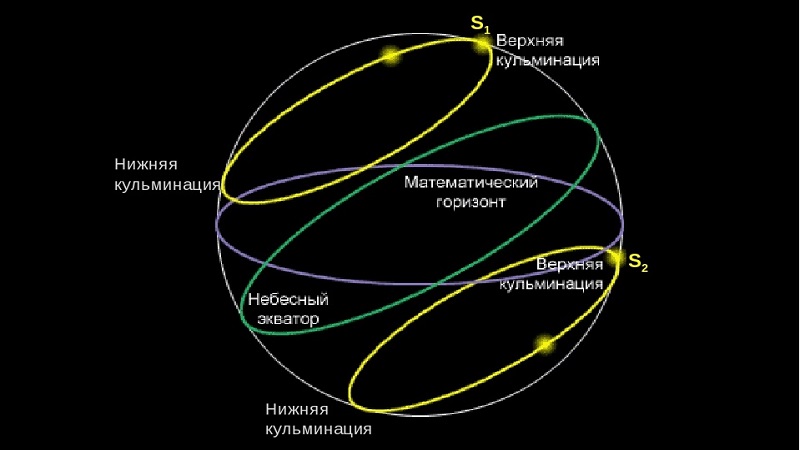
Кульминация звёзд

Кульминация звёзд

Стоит напомнить, что небесный меридиан является кругом сферы неба, который проходить сквозь зенит, полюс мира, а также южный полюс мира и надир.

Полюс мира представляет собой, можно сказать, отправную точку. Она лежит на небесной сфере, и как раз вокруг неё происходит видимое суточное движение звёзд. Причем перемещаются они по кругу параллельно экватору.

На Земле, как и в космосе — всегда есть на что посмотреть. Например сериалы Нетфликс, которые не оставят вас равнодушными.

Небесная сфера

Небесная сфера

Какая бывает кульминация звезд

Любое светило в течение суток пересекает меридиан неба в двух точках. Другими словами, вот этот момент и называется кульминацией.
Период между описываемым пересечением звёздных тел составляет половину суток, то есть 12 часов.

Так как кульминация звёзд происходит два раза за сутки, то она бывает двух видов:

  • верхняя, когда высота светила достигает максимального значения;
  • нижняя, наоборот, наступает в то время, когда высота звезды минимальна.

Как рассчитывается кульминация звёзд

Поскольку высота полюса мира над горизонтом равна географической широте местности, то определить значения момента пересечений звёздного тела и небесного меридиана не так уж сложно.

В действительности, верхняя и нижняя кульминация звезды рассчитывается по формуле:

Формулы определения кулиминаций

Формулы определения кулиминаций

где h — высота, ф — географическая широта и δ — склонение.

Получается, что если известно склонение и высота звезды в момент кульминации, то можно рассчитать географическую широту местности, откуда проводятся наблюдения.

Что интересно, незаходящая звезда для определённой географической широты наблюдается и в верхней, и в нижней кульминации. А вот если светило находится далеко от небесного экватора в сторону юга, то его пересечение с меридианом может быть незаметно.

Звёзды в космосе

Звёзды в космосе

Для понимания, как и когда происходит кульминация звёзд можно обратиться к нашему главному светилу. Правда, самый простой пример, это Солнце. Оно, как и другие звёзды, два раза в сутки пересекает небесный меридиан. И все мы хорошо знаем это время. Во-первых, верхняя солнечная кульминация-это полдень. Во-вторых, спустя половину суток (12 часов), наступает полночь или нижняя кульминация.

Как видно, люди долгое время наблюдали за движением небесных тел. Они выделили определённые особенности и научились применять их в своей жизни. В целом, само наблюдение за загадочными и светящимися звёздными точками, небесной сферой и космосом безумно увлекательное и красивое зрелище.

Оценка статьи:

Загрузка…

Источник

У этого термина существуют и другие значения, см. Кульминация.

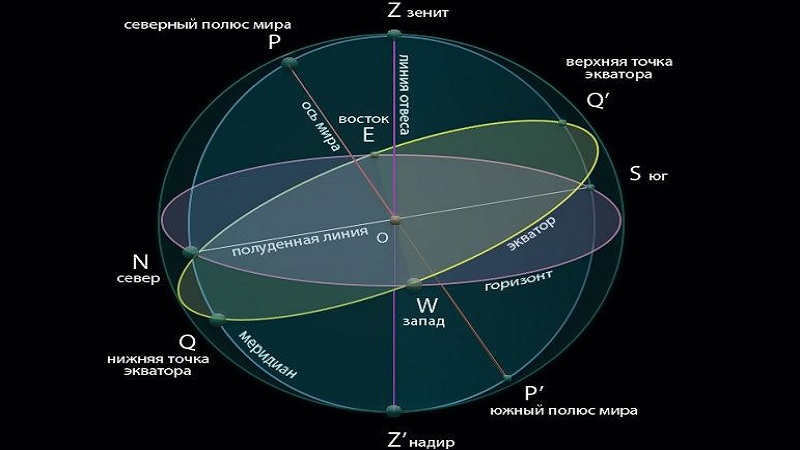
PS — повышенный полюс (в данном случае — южный), линия NS — горизонт наблюдателя, ZZ’ — отвесная линия, QQ’ — экватор. Линия AA’ — суточная параллель светила. Угол φ — широта местоположения наблюдателя, δ — склонение светила, z↑ — зенитное расстояние в верхней кульминации, z↓ — в нижней.

Кульминация (астрономия) — прохождение центра светила через небесный меридиан в процессе его суточного движения. Иначе — прохождение центром светила точки пересечения суточной параллели светила и небесного меридиана.

В течение суток все светила дважды пересекают небесный меридиан. Различают верхнюю и нижнюю кульминации светила. При условии, что величина склонения светила не меняется в течение дня, в верхней кульминации высота светила наибольшая, а в нижней — наименьшая. Для незаходящих светил обе кульминации происходят над горизонтом. Для восходящих и заходящих светил верхняя кульминация происходит над горизонтом, а нижняя под горизонтом. У невосходящих светил обе кульминации происходят под горизонтом и они недоступны наблюдениям[1].

Также различают верхнюю кульминацию к северу и к югу от зенита. Если светило кульминирует к югу от зенита, то в момент кульминации его астрономический азимут равен 0°, а если светило кульминирует к северу от зенита, то его азимут в момент кульминации равен 180°.

Зная склонение светила delta и широту места наблюдения varphi , можно вычислить зенитные расстояния этого светила в моменты кульминаций, при верхней:

{displaystyle z_{uparrow }=varphi -delta }

При нижней:

{displaystyle z_{downarrow }=(varphi +delta )-2varphi _{eP}}

где {displaystyle varphi _{eP}} — широта повышенного полюса: {displaystyle +90^{circ }} для наблюдателя в северном полушарии, {displaystyle -90^{circ }} в южном.

Подобно тому, как северную географическую широту и северное склонение принято считать положительными величинами, а южную — отрицательными, можно присвоить знак и зенитному расстоянию. Удобно пользоваться правилом: если тень наблюдателя (действительная или воображаемая) от светила падает в северную — положительную — сторону, то и зенитное расстояние светила положительно, если в южную, — зенитное расстояние отрицательно. То же правило получается из рассмотрения астрономического азимута светила: при кульминации южнее зенита астрономический азимут светила равен 0°, и {displaystyle cos(0^{circ })=+1}; при кульминации севернее зенита азимут равен 180°, {displaystyle cos(180^{circ })=-1}. Алгебраически знак зенитных расстояний получится при вычислениях, соблюдающих соглашения о знаках широт и склонений.

Наблюдая какое-либо светило в верхней и нижней кульминации, можно определить его склонение, а также широту места наблюдения:

{displaystyle delta =varphi _{eP}-{frac {z_{uparrow }-z_{downarrow }}{2}}}

{displaystyle varphi =varphi _{eP}+{frac {z_{uparrow }+z_{downarrow }}{2}}}

Наблюдая верхние кульминации звёзд по разные стороны от зенита на близких зенитных расстояниях, также можно определять широту. Для этого необходимо знать склонения обеих звёзд, зато точность такого измерения значительно возрастает. Этот метод известен как способ Талькотта. Если северная звезда находится в верхней кульминации, то формула принимает такой вид[2]:

{displaystyle varphi ={frac {(z_{S}-z_{N})+(delta _{S}+delta _{N})}{2}}}

Если же северная звезда находится в нижней кульминации, формула выглядит так:

{displaystyle varphi ={frac {(z_{S}-z_{N})+(180^{circ }+delta _{S}-delta _{N})}{2}}}

Индексы N и S обозначают зенитные расстояния и склонения для северной и южной звёзд соответственно.

См. также[править | править код]

  • Уравнение времени

Примечания[править | править код]

  1. ↑ 10. КУЛЬМИНАЦИЯ СВЕТИЛ. stu.sernam.ru. Дата обращения: 3 октября 2016. Архивировано 11 октября 2016 года.
  2. ↑ Серапинас Б. Б. Геодезические основы карт. Географический факультет МГУ. Дата обращения: 25 августа 2020. Архивировано 21 апреля 2021 года.

Литература[править | править код]

  • Кононович Э. В., Мороз В. И. — Общий курс астрономии, «Едиториал УРСС», 2001 (2-е изд. 2004)
  • В. Е. Жаров — Сферическая Астрономия, «Век-2», 2006

Ссылки[править | править код]

  • Сферическая астрономия В. Е. Жаров //3.6. Суточное вращение небесной сферы
Источник

На прошлых уроках мы с вами познакомились с картой
звёздного неба. Напомним, что так называют проекцию небесной сферы на
плоскость с нанесёнными на неё объектами в определённой системе координат.

Для построения звёздных карт за основной круг небесной сферы
обычно принимают круг небесного экватора. В этом случае небесные координаты
называются экваториальной системой координат. А координатами в ней служат
склонение и прямое восхождение.

Также мы с вами выяснили, что при суточном вращении звёздного
неба, Полярная звезда, располагающаяся вблизи Северного полюса мира, на данной
широте остаётся почти на одной высоте над горизонтом. Однако, если наблюдатель
начнёт перемещаться с севера на юг, где географическая широта меньше, то
Полярная звезда начнёт опускаться к горизонту.

Тогда логично предположить, что должна существовать некая
зависимость между высотой полюса мира и географической широтой места
наблюдения. Чтобы найти эту зависимость, давайте рассмотрим часть небесной
сферы и земной шар в проекции на плоскость небесного меридиана.

Пусть ОР — это часть оси мира, параллельная оси
вращения Земли; OQ — проекция части небесного экватора, параллельного экватору
Земли; OZ —
отвесная линия. Тогда наблюдатель, находящийся в точке О
будет видеть полюс мира на высоте, численно равной углу NOP.

Угол при центре Земли, образованный отвесной линией и
географическим экватором, соответствует географической широте места наблюдения.

Так как радиус Земли в точке наблюдения перпендикулярен
плоскости истинного горизонта, а ось мира перпендикулярна плоскости
географического экватора, то эти два угла равны между собой как углы со взаимно
перпендикулярными сторонами.

Таким образом получаем, что угловая высота полюса мира над
горизонтом равна географической широте места наблюдения.

Иными словами, измерив высоту полюса мира над горизонтом, мы
легко сможем определить географическую широту места, с которого производится
наблюдение.

Теперь обратите внимание на угол QOZ. Из рисунка видно, что это есть
ни что иное, как склонение зенита, которое равно географической широте места
наблюдения, а, следовательно, и высоте полюса мира над горизонтом.

Полученное нами равенство характеризует зависимость между
географической широтой места наблюдения и соответствующими горизонтальной и
экваториальной координатами светила.

Как мы с вами говорили на прошлом уроке, суточные пути светил
на небесной сфере — это окружности, плоскости которых параллельны небесному
экватору. А в зависимости от места наблюдения, характер суточного движения
звёзд, как и вид звёздного неба, меняется.

Проще всего разобраться в том, что и как происходит, на
полюсах Земли. Полюс — это такое место на земном шаре, где ось мира совпадает с
отвесной линией, а небесный экватор — с горизонтом. Для наблюдателя,
находящегося на Северном полюсе Земли, Полярная звезда будет располагаться в
зените, звёзды будут двигаться по кругам, параллельным математическому
горизонту, который совпадает с небесным экватором. При этом над горизонтом
будут видны все звёзды, склонение которых положительно (на Южном полюсе,
наоборот, будут видны все звезды, склонение которых отрицательно), а их высота
в течение суток не будет изменяться.

Переместимся в привычные для нас средние широты. Здесь уже
ось мира и небесный экватор наклонены к горизонту. Поэтому и суточные пути
звёзд также будут наклонены к горизонту. Следовательно, на средних широтах
наблюдатель сможет наблюдать восходящие и заходящие звёзды.

Под восходом понимается явление пересечения светилом
восточной части истинного горизонта, а под заходом — западной части этого
горизонта.

Помимо этого, часть звёзд, располагающихся в северных
околополярных созвездиях, никогда не будут опускаться за горизонт. Такие звёзды
принято называть незаходящими.

А звёзды, расположенные около Южного полюса мира для
наблюдателя на средних широтах будут являться невосходящими.

Отправимся дальше — на экватор, географическая широта
которого равна нулю. Здесь ось мира совпадает с полуденной линией (то есть
располагается в плоскости горизонта), а небесный экватор проходит через зенит.
Суточные пути всех, без исключения, звёзд перпендикулярны горизонту. Поэтому
находясь на экваторе, наблюдатель сможет увидеть все звёзды, которые в течение
суток восходят и заходят.

Вообще, для того, чтобы светило восходило и заходило, его
склонение по абсолютной величине должно быть меньше, чем .

Если ,
то в Северном полушарии она будет являться незаходящей (для Южного —
невосходящей).

Тогда очевидно, что те светила, склонение которых ,
являются невосходящими для Северного полушария (или незаходящими для Южного).

Для примера, давайте с вами по условиям восхода и захода,
определим, какой является звезда дельта Стрельца, для наблюдателя, находящего
на широте 55о 15’.

При суточном вращении все звёзды два раза пересекают небесный
меридиан. Это явление в астрономии получило название кульминацией светил.

Принято различать верхнюю и нижнюю кульминации. В момент
верхней кульминации светило достигает наивысшей точки над горизонтом, ближайшей
к зениту. Нижняя кульминация происходит через двенадцать часов после верхней
кульминации.

Теперь найдём формулу, по которой можно рассчитать высоту
светила в момент его верхней и нижней кульминаций. Для этого воспользуемся
небесной сферой и некоторыми её основными линиями.

Аналогичными рассуждениями можно получить формулу, определяющую
высоту светила в момент его верхней кульминации к северу от зенита:

Сравнив две формулы, не трудно найти и общую формулу высоты
светила в момент его верхней кульминации:

Здесь важно запомнить, что знак «плюс» перед скобками берётся
тогда, когда светило кульминирует к югу от зенита (то есть его склонение меньше
широты места наблюдения), а «минус», — когда к северу от зенита.

Предлагаем вам самостоятельно получить формулу для
определения высоты светила в момент его нижней кульминации.

Обратите внимание на то, что, измерив склонение светила и
его высоту в моменты кульминации, легко определить географическую широту, на
которой находится наблюдатель.

Для закрепления материала, давайте с вами решим такую задачу.

Источник

Добавить комментарий