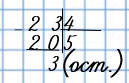Как найти остаток при делении двузначных чисел

План урока:

Случаи деления 80 : 20, 87 : 29

Деление с остатком

Решение задач на деление с остатком

Случаи деления, когда делитель больше делимого

Здравствуйте, ребята. Я, Знайка, продолжаю учить вас математике.

Выражение «твердый орешек» означает трудную для решения задачу. Орешек знанья тверд, но мы не привыкли отступать, вместе его расколем. Пусть скорлупа ореха — символ знания, ядро — опыт человечества. Математика раскроет тайны деления двузначных чисел, если будем стараться. Французский ученый Декарт говорил: «Умейте использовать свой хороший ум, чтобы справиться с задачами».

Начинайте, ребята, скорее работу,

Решайте, считайте, не сбивайтесь со счёта.

Случаи деления 80 : 20, 87 : 29

Начнем с деления на двузначное число.

Приемы деления вида 80 : 20

Приемы деления вида 87 : 29

Найдите значения двух выражений:

Для решения посмотрите на цифры единиц. Делитель заканчивается на 9. Вспомните таблицу умножения девяти. Какое произведение имеет семерку на конце? 27.

Других вариантов в таблице умножения на девять нет. Ответ равен трем.

Внимательно посмотрите на цифры в единицах. Делимое заканчивается на четверку. Вспомните множитель, который при умножении шести в произведении дает последнюю цифру четверку.

Это два случая: четыре, девять. В значениях произведений четверка на конце. Какой множитель подходит? Давайте посмотрим. Девять — многовато.

Задания легко решать, если знаешь таблицу умножения.

Деление столбиком на двузначное число

Вы уже знаете, что для записи действия деления применяют математический символ в виде двоеточия (∶), обелюса (÷), дробной (–), косой (∕) черты. Сегодня мы используем знак, который похож на лежащую боком букву.

При делении столбиком очень важна аккуратность, поэтому возьмите листок в клеточку.

Как записать решение примера 32 : 16 столбиком? Запишите каждую цифру делимого 32 в отдельную клеточку. Отступите одну клеточку вправо, запишите делитель 16. Проведите вертикальную и горизонтальную черточку.

Подбираем частное. Посмотрите на цифры единиц 2 и 6. Вспомните табличные случаи.

Семерка нам не подойдет, потому что 16 ∙ 7 — это большая величина. Значит, выбираем двойку. Проверяем: 16 ∙ 2 = 32. Записываем двойку на место частного под чертой. Вычитаем 32 из делимого. Пишем нуль. 32 разделили нацело.

Хорошо. А знаете ли вы, что с древних времён замечено влияние грецкого ореха на работу мозга. Как будто природа создала его, по форме извилин напоминающим полушария головного мозга. Благодаря работе этого центрального органа мы справляемся с математическими задачами.

Деление с остатком

Ребята, я предлагаю вам отправиться в путешествие по реке на лодках. Прежде чем отплыть от берега, нам нужно разделить 9 спасательных кругов на 2 лодки. Как узнать, сколько кругов окажется в одной лодке?

Верно, надо разделить. Запишите решение. Сколько получилось в выражении?

У вас трудности. Что заметили?

9 на 2 нацело не делится.

Почему не можем найти значение данного выражения?

Потому что это не табличный случай. Мы не умеем решать такие выражения.

Ребята, оказывается, в примерах может получиться остаток. Это арифметическое действие, играющее большую роль в математике и криптографии — науке о защите информации. В компьютерной технике тоже часто решают данные выражения.

Напишите отрезок натурального ряда от 17 до 37.

Выпишите из этого отрезка числа, которые делятся на 9.

Проверьте, это — 18, 27, 36.

Остаток при делении натуральных чисел 19, 28, 37 на 9 равен единице, потому что они следующие при счете.

Запишите отрезок натурального ряда от 11 до 25. Обведите числа, которые делятся на шесть нацело.

Укажите остатки при делении на 6 тринадцати и четырнадцати. Запишите выражения.

Проверьте:

Объясните, как рассуждали.

15 — на третьем месте после 12, 16 — четвертое место, а 17 – пятое место после 12.

Какой самый большой остаток получается при делении на 6?

Это пять, так как между величинами, которые делятся на шесть нацело, находится пять чисел.

Интересно знать! В Древнем Египте кушать ядра грецких орехов могли только высшие, самые главные жрецы. Для всех остальных, особенно для простого народа — это было запрещено. Чтобы не становились умнее и не начали много думать. Но мы с вами знаем пользу орехов и хорошо соображаем, поэтому продолжаем урок.

Деление с остатком на однозначное число

Существует два способа решения примеров.

1 способ деления на 5, 6, 7, 8, 9

Первый способ подходит, когда делитель равен или больше пяти. Мы должны найти в делимом наибольшее число, чтобы разделить, например, на семерку.

Как его отыскать? Посчитайте семерками. Если бы делили на пять, то считали бы пятерками, на шесть – шестерками и так далее.

Считаем семерками:

Разве 41 разделить на 7 — это пять? Нет, мы разделили только 35. Теперь найдем, сколько не разделили. Из 41 отнимите 35, получится шесть. Это искомый остаток.

Сделайте обязательный шаг — убедитесь, что остаток получился меньше чем делитель. Действительно 6 < 7. Правильное решение. Если получится больше, то нужно пересчитать заново.

Вычислите, чему равен частное и остаток при делении:

2 способ деления на 4, 3, 2 и 1

Второй способ подходит, когда делитель меньше пяти. Способ заключается в том, что делимое уменьшаем на 1 и проверяем, делится ли оно на делитель. Вы посмотрите:

Значит, вы можете применять оба способа в решении таких примеров.

Сорок пять меньше 52, а пятьдесят четыре больше. Значит, делим 45. Находим сколько осталось.

Лучше использовать второй способ. Вычитайте единицу.

Деление на двузначное число с остатком

Орешек знаний тверд, но мы его удачно раскалываем. Для решения таких примеров научимся работать не с самим числом, а с его десятками, но не с простыми, а округленными. Каким образом это работает?

Договоримся так: если количество единиц в числе меньше пяти, то есть — 1, 2, 3, 4, то количество десятков изменять не будем. Если же количество единиц в числе больше пяти, то есть — 5, 6,7, 9, то количество десятков увеличим на один.

Например, 96 разделим на 29. Каждое число округлим. У 96-и девять десятков, да шестерка даст еще один десяток. Округлим 96 до десяти десятков. 29 имеет два десятка и один десяток даст девятка, потому что она больше пяти.

Получается, что надо 10 десятков разделить на три десятка. Воспользуемся вторым способом. Уменьшим 10 на единицу, получаем 9.

Особенность в решении таких примеров в том, что не надо сразу писать ответ. Держите под рукой черновик и проверяйте решение. Чтобы проверить, не ошиблись ли, надо:

Решим следующий пример, где этот метод не работает. 77 – семь десятков да семерка в единицах дает еще один десяток. 13 округляем до десяти.

Получается, что пример сводится к делению восьми на один. Но восьмерка не подходит. 13 ∙ 7 явно больше 77. Поэтому пробуем шестерку. Видите, шестерка не подошла.

Уменьшаем еще на один. Получаем пять.

Полезно знать, что употреблять грецкие орехи нужно взрослым и детям. Важно это делать правильно и регулярно. Тогда вы получите максимальную пользу от этого ценного продукта.

Продолжим урок математики.

Деление с остатком столбиком

В 52 содержится 6 раз по 8, остаётся 4.

52 : 8 = 6 (ост. 4)

Пример с остатком запишите в виде деления в столбик:

1. Делимое 52 напишите слева, правее — делитель 8. Между ними проведите вертикальную черту в две клетки — знак деления, горизонтальной линией подчеркните делитель.
2. Сколько делителей 8 помещается в делимом 52? Вспомните табличный случай 8 ∙ 6 = 48. Запишите неполное частное 8 в форму.
3. Найдите остаток. 48 вычтите из делимого. Проведите черту. Это знак равно. Запишите 4. 

Напоминаю: сравните остаток и делитель. 4 < 6. Пример решили верно.

Выполните деления с остатком 51 : 7 =

Ближайшее к делимому будет табличное произведение 49.

2 < 7. Значит, пример решили правильно.

Проверка деления с остатком

Но случаются ошибки. Проверить решения можно обратными действиями.

Выполните деление с остатком и сделайте проверку:

Убедиться в правильности решения помогает проверка.

Сравните: 6 < 12. 

Решение задач на деление с остатком

Простые задачи легко решить, если составить модель-схему условия и решения задачи на числовом луче.

Рассмотрите пример задачи:

Повар испек 17 творожных и 19 брусничных ватрушек. На тарелки положит по три штуки одного сорта. Узнайте, сколько нужно тарелок и сколько ватрушек останется.

Решение:

Ответ: для творожных ватрушек нужно 5 тарелок, две останутся; для брусничных — 5 тарелок, одна ватрушка останется.

Составьте задачу на деление с остатком, выбрав подходящее выражение:

Проверьте рассуждение. Для задачи подойдет второе выражение, а первое и последнее – не подходят, потому что это табличные случаи.

Пример задачи: На пальто пришивается 4 пуговицы. На сколько таких пальто хватит 15 пуговиц? Сколько пуговиц останется?

Ответ: пуговиц хватит на три пальто. Останется 3 пуговицы.

Придумайте задачу к схеме:

Мама купила 21 конфету и поделила по 8 штук детям. Сколько детей в семье и сколько конфет мама оставила себе?

Решение:

21 : 8 = 2 (ост.5)

Ответ: в семье двое детей. Мама оставила 5 конфет.

Умения решать задачи по математике помогают в жизни.

Незнайка отправился в магазин. У него есть 90 рублей, и он хочет купить мороженое по цене 28 рублей. Сколько стаканчиков с мороженым сможет купить Незнайка и сколько денег у него останется?

Подсказка: решить задачу можно округлив величины. 90 – это девять десятков, а 28 округлим до трех десятков.

Проверьте:

Ответ: Незнайка купит 3 стаканчика с мороженным. У него останется 6 рублей.

Случаи деления, когда делитель больше делимого

В конце урока Орешек принес интересный пример:

Делитель 9 больше делимого 7. Как решить?

Сколько раз по девять содержится в семи? Конечно — нуль раз. В частном запишите 0. Нуль умножить на девять получится нуль. Вычитаем 0. Остаток 7.

Ребята, наш урок подошёл к концу.

Математика. 3 класс

Урок № 49. Проверка деления с остатком

Перечень вопросов, рассматриваемых в теме:

1. Как разделить двузначное число на двузначное с остатком?

2. Как выполнить проверку деления с остатком?

3. Какие приёмы проверки частного и остатка удобные?

Глоссарий по теме:

Деление – это обратное действие умножению.

Делимое – компонент деления, число которое делят.

Делитель – компонент деления, число на которое делят.

Частное – результат деления.

Неполное частное – результат деления с остатком.

Обязательная литература и дополнительная литература:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для

общеобразовательных организаций М.; Просвещение, 2017. – с. 32.

2. Математика. 3 класс. Часть 2. / Л. Г. Петерсон. – М.: Ювента, 2013 – с. 96.

Теоретический материал для самостоятельного изучения

Ребята, вы уже знакомы со случаями деления с остатком. Теперь нам нужно научиться выполнять проверку деления двузначного на двузначное с остатком.

Рассмотрим пример.

Восемьдесят пять разделить на пятнадцать – получим частное пять и остаток десять.

85 : 15 = 5 (ост. 10)

Выполним проверку.

Первое в чём должны убедиться, это в том, что остаток меньше делителя.

Десять меньше пятнадцати.

10 < 15

Далее делитель умножаем на частное:

пятнадцать умножаем на пять получается семьдесят пять и прибавляем остаток десять. Получаем делимое – восемьдесят пять.

15 ∙ 5 + 10 = 85

В случае деления, когда делимое меньше делителя, действуем так же.

Девятнадцать разделить на двадцать равно нулю и остаток девятнадцать. Девятнадцать меньше двадцати.

Двадцать умножаем на нуль и прибавляем девятнадцать равно девятнадцати.

19 : 20 = 0 (ост. 19)

Проверка: 1) 19 < 20,

2) 20 ∙ 0 + 19 = 19

Выполним тренировочные задания.

№1. Как проверить деление 34 : 16 = 2 (ост. 2)?

1) 2 ∙ 16 + 2 = 34;

2) 2 ∙ 16 = 34;

Ответ: 2 ∙ 16 + 2 = 34.

№ 2. Вставьте пропущенные числа:

49 : 15 = ____ (ост. ___)

15 ∙ ___ + ____ = 49

Ответ: 49 : 15 = 3 (ост. 4)

15 ∙ 3 + 4 = 49

№ 3. Соотнесите условие задачи, решение и проверку:

«40 банок с вареньем упаковывали в ящики по 6 штук. Сколько ящиков потребовалось? Сколько банок осталось?»

40 : 6 = 6 (ост. 3) — 6 ∙ 6 + 3 = 40

40 : 6 = 5 (ост. 10) — 6 ∙ 5 + 10 = 40

40 : 6 = 6 (ост. 4) — 6 ∙ 6 + 4 = 40

Ответ: 40 : 6 = 6 (ост. 4) — 6 ∙ 6 + 4 = 40

№ 4. Решите примеры и укажите, какой остаток получится при делении:

57 : 42;

28 : 17;

89 : 22;

5 : 11.

Правильный вариант:

Остаток больше 10

57 : 42 28 : 17

Остаток меньше 10

89 : 22 5 : 11

№ 5. Расшифруйте слово. Что оно означает в математике?

Ответ:

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Деление
5. Деление с остатком

Советуем посмотреть:

Табличное деление

Внетабличное деление

Деление суммы на число

Деление на однозначное число

Деление чисел, оканчивающихся нулями

Свойства деления

Деление

Правило встречается в следующих упражнениях:

2 класс

Страница 76. Урок 29,
Петерсон, Учебник, часть 3

Страница 77. Урок 29,
Петерсон, Учебник, часть 3

Страница 79. Урок 30,
Петерсон, Учебник, часть 3

Страница 80. Урок 30,
Петерсон, Учебник, часть 3

Страница 81. Урок 31,
Петерсон, Учебник, часть 3

Страница 82. Урок 31,
Петерсон, Учебник, часть 3

Страница 84. Урок 32,
Петерсон, Учебник, часть 3

Страница 87. Урок 33,
Петерсон, Учебник, часть 3

Страница 108. Повторение,
Петерсон, Учебник, часть 3

3 класс

Страница 20,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 29,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 100,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 31,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 40,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 73,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 24. Урок 8,
Петерсон, Учебник, часть 1

Страница 92. Урок 34,
Петерсон, Учебник, часть 1

4 класс

Страница 20,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 38,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 61,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 39,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 60. ПР 1. Вариант 1,
Моро, Волкова, Проверочные работы

Страница 18,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 31,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

5 класс

Задание 531,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 599,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1083,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1087,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1160,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1161,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2

Номер 671,
Мерзляк, Полонский, Якир, Учебник

Номер 1091,
Мерзляк, Полонский, Якир, Учебник

Номер 1222,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 358,
Мерзляк, Полонский, Якир, Учебник

Номер 366,
Мерзляк, Полонский, Якир, Учебник

Номер 500,
Мерзляк, Полонский, Якир, Учебник

Номер 727,
Мерзляк, Полонский, Якир, Учебник

Номер 730,
Мерзляк, Полонский, Якир, Учебник

Номер 1150,
Мерзляк, Полонский, Якир, Учебник

Номер 6,
Мерзляк, Полонский, Якир, Учебник

Номер 2,
Мерзляк, Полонский, Якир, Учебник

Задание 515,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 578,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 47,
Мерзляк, Полонский, Якир, Учебник

Номер 330,
Мерзляк, Полонский, Якир, Учебник

Номер 529,
Мерзляк, Полонский, Якир, Учебник

Номер 556,
Мерзляк, Полонский, Якир, Учебник

Номер 580,
Мерзляк, Полонский, Якир, Учебник

Номер 581,
Мерзляк, Полонский, Якир, Учебник

Номер 583,
Мерзляк, Полонский, Якир, Учебник

Номер 608,
Мерзляк, Полонский, Якир, Учебник

Номер 772,
Мерзляк, Полонский, Якир, Учебник

Номер 797,
Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 4,
Мерзляк, Полонский, Якир, Учебник

Номер 46,
Мерзляк, Полонский, Якир, Учебник

Номер 141,
Мерзляк, Полонский, Якир, Учебник

Номер 193,
Мерзляк, Полонский, Якир, Учебник

Номер 207,
Мерзляк, Полонский, Якир, Учебник

Номер 241,
Мерзляк, Полонский, Якир, Учебник

Номер 254,
Мерзляк, Полонский, Якир, Учебник

Номер 302,
Мерзляк, Полонский, Якир, Учебник

Номер 304,
Мерзляк, Полонский, Якир, Учебник

Номер 307,
Мерзляк, Полонский, Якир, Учебник

---

Учитель начальных классов

Как делить числа с остатком? Деление на двузначное число с остатком.

Здравствуйте, друзья! Сегодня мы поговорим про то, как делить числа с остатком. Так же в этом видео мы разберем следующие темы: деление на двузначное число с остатком и деление с остатком однозначных чисел. Если вы не знаете, как делать деление с остатком, то смотрите это видео до конца, я думаю у нас получится разобраться. Видео будет полезно и родителем, вы узнаете, как объяснить ребенку деление с остатком. В этом видео я покажу вам Метод деления с остатком, благодаря которому вы узнаете как делить двузначные числа с остатком. Этот Способ деления с остатком значительно проще, чем тот, который дают нам в учебниках, и решение задач на деление с остатком не составит для вас труда. В этом видео мы поговорим о том, как делить двузначное на двузначное с остатком и как решать примеры деление с остатком. Вы увидите что деление с остатком объяснение довольное простое.

1303

26.01.2021

«Свидетельство эксперта педагогического сообщества»

Оставляйте комментарии к работам коллег и получите документ
БЕСПЛАТНО!

Свидетельство активного участника педагогического сообщества

Оформить бесплатно документ можно здесь

Деление с остатком

• Как делить с остатком?
• Проверка деления с остатком

Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.

Как делить с остатком?

Выполнить деление не всегда возможно, так как бывают случаи, когда одно число не делится на другое. Например, число  11  не делится на  3,  так как нет такого натурального числа, при умножении которого на  3  получилось бы  11.

Когда деление невозможно выполнить условились делить не всё делимое, а только наибольшую его часть, какая только может разделиться на делитель. В данном примере наибольшая часть делимого, которая может быть разделена на  3  — это  9  (в результате получим  3),  оставшаяся меньшая часть делимого —  2  не разделится на  3.

Говоря о делении  11  на  3,  11  по прежнему называется делимым,  3  — делителем, результат деления — число  3,  называют неполным частным, а число  2  — остатком от деления. Само деление в этом случае называют делением с остатком.

Неполное частное — это наибольшее число, которое при умножении на делитель даёт произведение, не превосходящее делимого. Остаток — это разность между делимым и этим произведением. Остаток всегда меньше делителя, иначе его тоже можно было бы поделить на делитель.

Остаток всегда меньше делителя.

Деление с остатком можно записывать так:

27 : 7 = 3 (ост. 6),

где  27  — это делимое,  7  — делитель,  3  — неполное частное, а  6  — остаток.

Если при делении одного натурального числа на другое в остатке получается  0,  то говорят, что первое число делится на второе нацело. Например,  4  делится на  2  нацело. Число  5  не делится на  2  нацело. Слово нацело обычно опускают для краткости и говорят: такое-то число делится на другое, например:  4  делится на  2,  а  5  не делится на  2.

Проверка деления с остатком

Рассмотрим выражение:

15 : 2 = 7 (ост. 1),

где  15  — это делимое,  2  — делитель,  7  — неполное частное, а  1  — остаток.

Чтобы узнать правильно ли было выполнено деление с остатком, можно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, равное делимому, то деление с остатком выполнено верно:

7 · 2 + 1 = 15

или

2 · 7 + 1 = 15.