history 10 января 2021 г.
- Группы статей
Экспоненциальное сглаживание используется для сглаживания краткосрочных колебаний во временных рядах, чтобы облегчить определение долгосрочного тренда, а также для прогнозирования. Произведем экспоненциальное сглаживание с помощью надстройки MS EXCEL Пакет анализа и формулами. Рассмотрим двойное и тройное экспоненциальное сглаживание для прогнозирования рядов с трендом и сезонностью.
Экспоненциальное сглаживание один из наиболее распространённых методов для сглаживания временных рядов. В отличие от метода Скользящего среднего, где прошлые наблюдения имеют одинаковый вес, Экспоненциальное сглаживание присваивает им экспоненциально убывающие веса, по мере того как наблюдения становятся старше. Другими словами, последние наблюдения дают относительно больший вес при прогнозировании, чем старые наблюдения.
Примечание: Перед прочтением этой статьи рекомендуется прочитать про Скользящее среднее.
Примечание: В англоязычной литературе для экспоненциального сглаживания используется термин Single Exponential Smoothing или Simple Exponential Smoothing (SES).
Напомним, что при усреднении методом Скользящего среднего веса, присвоенные наблюдениям, одинаковы и равны 1/n, где n – количество периодов усреднения. Например, в случае усреднения за 3 периода скользящее среднее равно:
Yскол.i=(Yi+ Yi-1+ Yi-2)/3 = Yi/3+ Yi-1/3+ Yi-2/3
В случае Экспоненциального сглаживания формула выглядит следующим образом:
Yэксп.i=альфа*Yi-1+ (1-альфа)*Yэксп.i-1
или
Yэксп.i= Yэксп.i-1 + альфа*(Yi-1 – Yэксп.i-1)
где 0<альфа<1, i>2
Параметр альфа определяет степень сглаживания. При малых значениях альфа (0,1 – 0,2) имеет место сильное сглаживание. При значениях близких к 1, сглаженный ряд практически повторяет исходный ряд с задержкой (лагом) на один период. Для медленно меняющегося ряда часто берут небольшие значения альфа=0,1; а для быстро меняющегося 0,3-0,5.
Примечание: Формулы представляют собой рекуррентное соотношение – это когда последующий член ряда вычисляется на основе предыдущего.
Примечание: Существует альтернативный подход к Экспоненциальному сглаживанию: в нем в формуле вместо Yi-1 заменяют на Yi. Этот подход используется в контрольных картах экспоненциально взвешенного скользящего среднего (EWMA).
Надстройка Пакет анализа
Получить Экспоненциально сглаженный ряд можно с помощью надстройки Пакет анализа (Analysis ToolPak). Надстройка доступна из вкладки Данные, группа Анализ.
СОВЕТ: Подробнее о других инструментах надстройки Пакет анализа и ее подключении – читайте в статье.
Разместим исходный числовой ряд в диапазоне B7:B32.
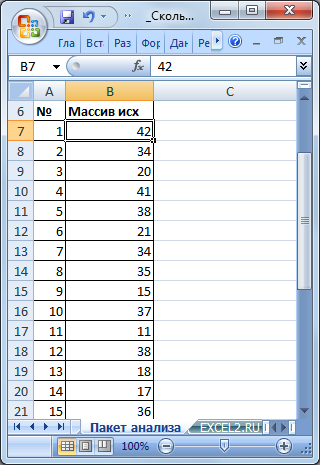
Для наглядности пронумеруем каждое значение ряда (столбец А).
Вызовем надстройку Пакет анализа, выберем инструмент Экспоненциальное сглаживание.
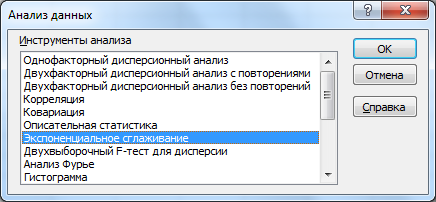
и нажмем ОК.
В появившемся диалоговом окне в поле Входной интервал введите ссылку на диапазон с данными ряда, т.е. на B7:B32.
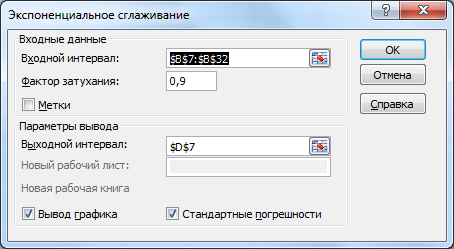
Если диапазон включает и заголовок, то нужно установить галочку в поле Метки. В нашем случае устанавливать галочку не требуется, т.к. заголовок столбца не входит в диапазон B7:B32.
Поле Фактор затухания, как и параметр альфа в вышеуказанной формуле, определяет степень сглаживания ряда. Фактор затухания равен (1- альфа). Чем больше Фактор затухания тем глаже получается ряд. Установим значение 0,8.
В поле Выходной интервал достаточно ввести ссылку на левую верхнюю ячейку диапазона с результатами (укажем ячейку D7).
Также поставим галочки в поле Вывод графика и Стандартные погрешности (будет выведен столбец с расчетами погрешностей, англ. Standard Errors).
Нажмем ОК.
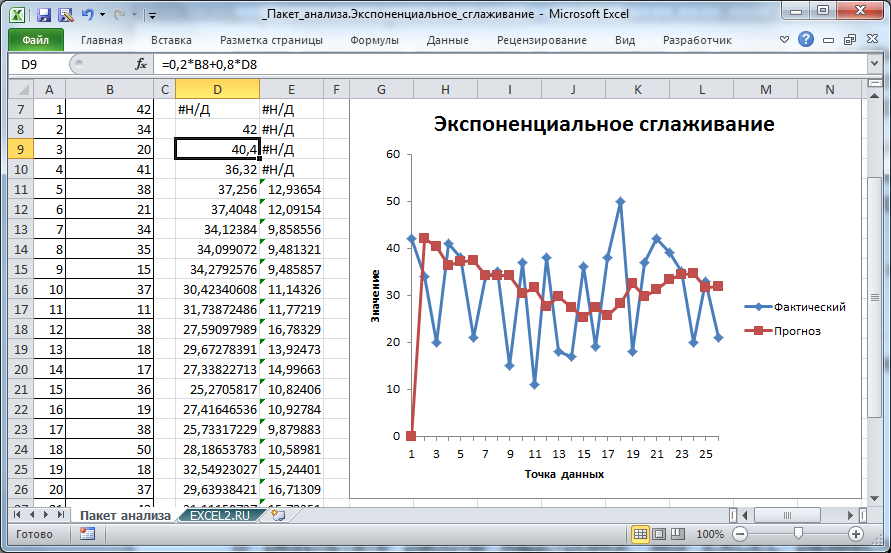
В результате работы надстройки, MS EXCEL разместил значения ряда, полученного методом Экспоненциального сглаживания, в столбце D (см. файл примера лист Пакет анализа).
В ячейке D7 содержится текстовое значение ошибки #Н/Д, т.к. для получения первого значения Экспоненциального сглаживания требуется значение исходного ряда за предыдущий период.
Первое значение сглаженного ряда, точнее формула =B7, содержится в ячейке D8. Второе значение вычисляется с помощью формулы =0,2*B8+0,8*D8.
Таким образом, Фактор затухания (0,8) определяет вес (вклад) предыдущего значения сглаженного ряда. Соответственно, (1-Фактор затухания)=альфа определяет вес предыдущего значения исходного ряда.
Диаграмма
Для отображения рядов MS EXCEL создал диаграмму типа график. Сглаженный ряд на диаграмме называется «Прогноз» (ряд красного цвета).
Первое значение сглаженного ряда, которое равно ошибке #Н/Д, отражаются как 0, и может ввести в заблуждение (особенно, если последующие значения ряда близки к 0). Поэтому его лучше удалить из ячейки D7.
Примечание: Значение #Н/Д в ячейке D7 является просто текстовым значением, что принципиально отличается от результата возвращаемого формулами, например, функцией НД(), хотя визуально они неразличимы. При построении диаграммы текстовые значения всегда отображаются как 0. Но, если ошибка #Н/Д является результатом формулы, то воспринимается диаграммой как пустая ячейка и на ней не отображается.
Диаграмма позволяет визуально определить «выбросы», т.е. значения исходного ряда, которые существенно отличаются от средних значений. Такие «выбросы» могут быть следствием ошибки, но они оказывают существенное влияние на вид сглаженного ряда.
Вычисление погрешности
В столбце E, начиная с ячейки Е11, MS EXCEL разместил формулы для вычисления погрешностей (англ. Standard Errors):
=КОРЕНЬ(СУММКВРАЗН(B8:B10;D8:D10)/3)
Т.е. данная погрешность вычисляется по формуле:
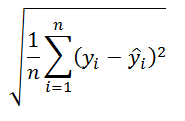
Значения y – это значения исходного ряда в период i. Значения «y с крышечкой» – значения ряда, полученного методом Экспоненциального сглаживания, в тот же в период i. Значение n для экспоненциального сглаживания всегда равно 3, т.е. ошибка вычисляется за 3 последних периода (последние 3 значения учитываются с макимальным весом при расчете текущего значения сглаженного ряда и, соответственно, вносят более 50% вклада в его значение. Величина вклада сильно зависит от альфа).
Подробнее об этой погрешности см. соответствующий раздел в статье про Скользящее среднее.
Почему сглаживание называется экспоненциальным?
Как было показано в статье про Взвешенное скользящее среднее веса значений исходного ряда берутся в зависимости от их удаленности от текущего периода. Например, для 3-х периодов усреднения для Взвешенного скользящего среднего можно использовать формулу:
Yскол.i=0,5*Yi+ 0,4*Yi-1+ 0,1*Yi-2
Экспоненциальное сглаживание по сути является модификацией Взвешенного скользящего среднего – при расчете значения сглаженного ряда используются ВСЕ предыдущие значения исходного ряда с весами уменьшающимися в геометрической прогрессии по мере удаления от текущего периода.
Чтобы это показать воспользуемся формулой
Yэксп.i=альфа*Yi-1+ (1-альфа)*Yэксп.i-1
и вычислим Yэксп.5, т.е. значения сглаженного ряда для 5-го периода. После очевидных преобразований получим:
Yэксп.5=альфа*[(1-альфа)0* Yэксп.4+ (1-альфа)1* Yэксп.3+(1-альфа)2* Yэксп.2] +(1-альфа)3* Y1
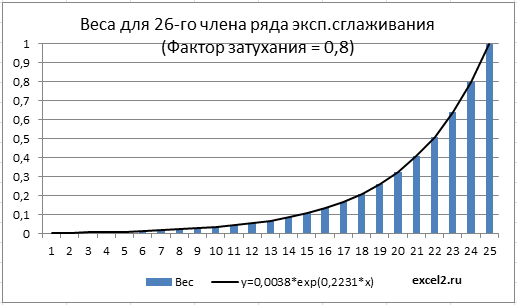
Таким образом, вес 4-го (предыдущего) члена ряда =(1-альфа)0, а вес 3-го =(1-альфа)1 и т.д. Пусть t – текущий период (в нашем случае =5). Вес (t-i)-го члена ряда =(1-альфа)t-1-i. Т.к. (1-альфа)<1, то с ростом i растет и вес, и для члена t-1 достигает максимума =1.
Как известно, экспоненциальный рост y=a*EXP(b*x) в случае дискретной области определения с равными интервалами x называют геометрическим ростом (значения экспоненциальной функции y=a*EXP(b*x) являются в этом случае членами геометрической прогрессии m^x).
В нашем случае, приравняв i-й вес (1-альфа)t-1-i соответствующему значению экспоненциальной функции a*EXP(b*i) получим уравнение, которое позволит вычислить коэффициенты a и b (понадобится еще одно уравнение, например, для i-1 веса).
Решив систему из 2-х уравнений получим, a= EXP((t-1)*LN(1-альфа)) и b= LN(1-альфа).
В файле примера для 26-го члена сглаженного ряда (t=26) вычислены веса всех предыдущих членов. На диаграмме ниже показано, что веса уменьшаются с ростом i в геометрической прогрессии, что соответствует экспоненциальной функции y=0,0038*exp(0,2231*x), где x=i. Вычисления параметров экспоненциальной кривой сделаны с помощью надстройки Поиск решения.
Экспоненциальное сглаживание с настраиваемым Фактором затухания
Недостатком формул, получаемых с помощью Пакета анализа, является то, что при изменении Фактора затухания (1-альфа) приходится перезапускать расчет. В файле примера на листе Формулы создана форма для быстрого пересчета Экспоненциального сглаживания в зависимости от значения Фактора затухания (полученный результат, естественно, полностью совпадает с расчетами надстройки Пакет анализа).
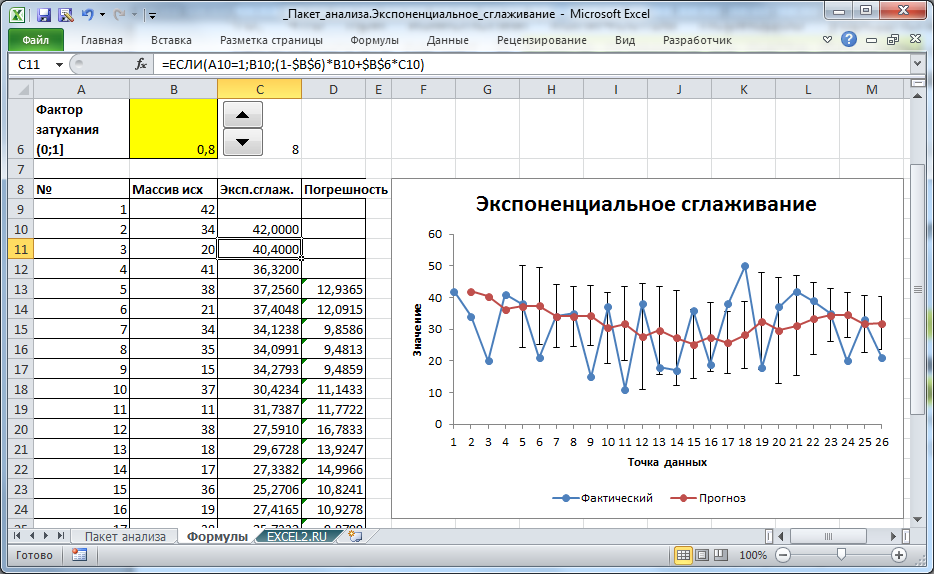
Значения ряда вычисляются с помощью формулы:
=ЕСЛИ(A10=1;B10;(1-$B$6)*B10+$B$6*C10)
в ячейке В6 содержится значение Фактора затухания.
Выбор значения Фактора затухания для удобства осуществляется с помощью элемента управления Счетчик с шагом 0,1.
Exponential smoothing is a rule of thumb technique for smoothing time series data using the exponential window function. Whereas in the simple moving average the past observations are weighted equally, exponential functions are used to assign exponentially decreasing weights over time. It is an easily learned and easily applied procedure for making some determination based on prior assumptions by the user, such as seasonality. Exponential smoothing is often used for analysis of time-series data.
Exponential smoothing is one of many window functions commonly applied to smooth data in signal processing, acting as low-pass filters to remove high-frequency noise. This method is preceded by Poisson’s use of recursive exponential window functions in convolutions from the 19th century, as well as Kolmogorov and Zurbenko’s use of recursive moving averages from their studies of turbulence in the 1940s.
The raw data sequence is often represented by 




where 

Basic (simple) exponential smoothing[edit]
The use of the exponential window function is first attributed to Poisson[2] as an extension of a numerical analysis technique from the 17th century, and later adopted by the signal processing community in the 1940s. Here, exponential smoothing is the application of the exponential, or Poisson, window function. Exponential smoothing was first suggested in the statistical literature without citation to previous work by Robert Goodell Brown in 1956,[3] and then expanded by Charles C. Holt in 1957.[4] The formulation below, which is the one commonly used, is attributed to Brown and is known as “Brown’s simple exponential smoothing”.[5] All the methods of Holt, Winters and Brown may be seen as a simple application of recursive filtering, first found in the 1940s[2] to convert finite impulse response (FIR) filters to infinite impulse response filters.
The simplest form of exponential smoothing is given by the formula:
where 




The term smoothing factor applied to 




There is no formally correct procedure for choosing 



Unlike some other smoothing methods, such as the simple moving average, this technique does not require any minimum number of observations to be made before it begins to produce results. In practice, however, a “good average” will not be achieved until several samples have been averaged together; for example, a constant signal will take approximately 
This simple form of exponential smoothing is also known as an exponentially weighted moving average (EWMA). Technically it can also be classified as an autoregressive integrated moving average (ARIMA) (0,1,1) model with no constant term.[7]
Time constant[edit]
The time constant of an exponential moving average is the amount of time for the smoothed response of a unit step function to reach 


, thus
where 

Choosing the initial smoothed value[edit]
Note that in the definition above, 



Optimization[edit]
For every exponential smoothing method we also need to choose the value for the smoothing parameters. For simple exponential smoothing, there is only one smoothing parameter (α), but for the methods that follow there is usually more than one smoothing parameter.
There are cases where the smoothing parameters may be chosen in a subjective manner – the forecaster specifies the value of the smoothing parameters based on previous experience. However, a more robust and objective way to obtain values for the unknown parameters included in any exponential smoothing method is to estimate them from the observed data.
The unknown parameters and the initial values for any exponential smoothing method can be estimated by minimizing the sum of squared errors (SSE). The errors are specified as 

[10]
Unlike the regression case (where we have formulae to directly compute the regression coefficients which minimize the SSE) this involves a non-linear minimization problem and we need to use an optimization tool to perform this.
“Exponential” naming[edit]
The name ‘exponential smoothing’ is attributed to the use of the exponential window function during convolution. It is no longer attributed to Holt, Winters & Brown.
By direct substitution of the defining equation for simple exponential smoothing back into itself we find that
In other words, as time passes the smoothed statistic 

A geometric progression is the discrete version of an exponential function, so this is where the name for this smoothing method originated according to Statistics lore.
Comparison with moving average[edit]
Exponential smoothing and moving average have similar defects of introducing a lag relative to the input data. While this can be corrected by shifting the result by half the window length for a symmetrical kernel, such as a moving average or gaussian, it is unclear how appropriate this would be for exponential smoothing. They also both have roughly the same distribution of forecast error when α = 2/(k + 1). They differ in that exponential smoothing takes into account all past data, whereas moving average only takes into account k past data points. Computationally speaking, they also differ in that moving average requires that the past k data points, or the data point at lag k + 1 plus the most recent forecast value, to be kept, whereas exponential smoothing only needs the most recent forecast value to be kept.[11]
In the signal processing literature, the use of non-causal (symmetric) filters is commonplace, and the exponential window function is broadly used in this fashion, but a different terminology is used: exponential smoothing is equivalent to a first-order infinite-impulse response (IIR) filter and moving average is equivalent to a finite impulse response filter with equal weighting factors.
Double exponential smoothing (Holt linear)[edit]
Simple exponential smoothing does not do well when there is a trend in the data. [1] In such situations, several methods were devised under the name “double exponential smoothing” or “second-order exponential smoothing,” which is the recursive application of an exponential filter twice, thus being termed “double exponential smoothing”. This nomenclature is similar to quadruple exponential smoothing, which also references its recursion depth.[12]
The basic idea behind double exponential smoothing is to introduce a term to take into account the possibility of a series exhibiting some form of trend. This slope component is itself updated via exponential smoothing.
One method, works as follows:[13]
Again, the raw data sequence of observations is represented by 









And for 
where 



To forecast beyond 
Setting the initial value 


Note that F0 is undefined (there is no estimation for time 0), and according to the definition F1=s0+b0, which is well defined, thus further values can be evaluated.
A second method, referred to as either Brown’s linear exponential smoothing (LES) or Brown’s double exponential smoothing works as follows.[14]
where at, the estimated level at time t and bt, the estimated trend at time t are:
Triple exponential smoothing (Holt Winters)[edit]
Triple exponential smoothing applies exponential smoothing three times, which is commonly used when there are three high frequency signals to be removed from a time series under study. There are different types of seasonality: ‘multiplicative’ and ‘additive’ in nature, much like addition and multiplication are basic operations in mathematics.
If every month of December we sell 10,000 more apartments than we do in November the seasonality is additive in nature. However, if we sell 10% more apartments in the summer months than we do in the winter months the seasonality is multiplicative in nature. Multiplicative seasonality can be represented as a constant factor, not an absolute amount.
[15]
Triple exponential smoothing was first suggested by Holt’s student, Peter Winters, in 1960 after reading a signal processing book from the 1940s on exponential smoothing.[16] Holt’s novel idea was to repeat filtering an odd number of times greater than 1 and less than 5, which was popular with scholars of previous eras.[16] While recursive filtering had been used previously, it was applied twice and four times to coincide with the Hadamard conjecture, while triple application required more than double the operations of singular convolution. The use of a triple application is considered a rule of thumb technique, rather than one based on theoretical foundations and has often been over-emphasized by practitioners.
–
Suppose we have a sequence of observations 


The method calculates a trend line for the data as well as seasonal indices that weight the values in the trend line based on where that time point falls in the cycle of length 
Let 







The output of the algorithm is again written as 



where 





The general formula for the initial trend estimate 
Setting the initial estimates for the seasonal indices 


where
Note that 


Triple exponential smoothing with additive seasonality is given by:
Implementations in statistics packages[edit]
- R: the HoltWinters function in the stats package[17] and ets function in the forecast package[18] (a more complete implementation, generally resulting in a better performance[19]).
- Python: the holtwinters module of the statsmodels package allow for simple, double and triple exponential smoothing.
- IBM SPSS includes Simple, Simple Seasonal, Holt’s Linear Trend, Brown’s Linear Trend, Damped Trend, Winters’ Additive, and Winters’ Multiplicative in the Time-Series modeling procedure within its Statistics and Modeler statistical packages. The default Expert Modeler feature evaluates all seven exponential smoothing models and ARIMA models with a range of nonseasonal and seasonal p, d, and q values, and selects the model with the lowest Bayesian Information Criterion statistic.
- Stata: tssmooth command[20]
- LibreOffice 5.2[21]
- Microsoft Excel 2016[22]
See also[edit]
- Autoregressive moving average model (ARMA)
- Errors and residuals in statistics
- Moving average
- Continued fraction
Notes[edit]
- ^ a b c “NIST/SEMATECH e-Handbook of Statistical Methods”. NIST. Retrieved 23 May 2010.
- ^ a b Oppenheim, Alan V.; Schafer, Ronald W. (1975). Digital Signal Processing. Prentice Hall. p. 5. ISBN 0-13-214635-5.
- ^ Brown, Robert G. (1956). Exponential Smoothing for Predicting Demand. Cambridge, Massachusetts: Arthur D. Little Inc. p. 15.
- ^ Holt, Charles C. (1957). “Forecasting Trends and Seasonal by Exponentially Weighted Averages”. Office of Naval Research Memorandum. 52. reprinted in Holt, Charles C. (January–March 2004). “Forecasting Trends and Seasonal by Exponentially Weighted Averages”. International Journal of Forecasting. 20 (1): 5–10. doi:10.1016/j.ijforecast.2003.09.015.
- ^ Brown, Robert Goodell (1963). Smoothing Forecasting and Prediction of Discrete Time Series. Englewood Cliffs, NJ: Prentice-Hall.
- ^ “NIST/SEMATECH e-Handbook of Statistical Methods, 6.4.3.1. Single Exponential Smoothing”. NIST. Retrieved 5 July 2017.
- ^ Nau, Robert. “Averaging and Exponential Smoothing Models”. Retrieved 26 July 2010.
- ^ “Production and Operations Analysis” Nahmias. 2009.
- ^ Čisar, P., & Čisar, S. M. (2011). “Optimization methods of EWMA statistics.” Acta Polytechnica Hungarica, 8(5), 73–87. Page 78.
- ^ 7.1 Simple exponential smoothing | Forecasting: Principles and Practice.
- ^ Nahmias, Steven (3 March 2008). Production and Operations Analysis (6th ed.). ISBN 978-0-07-337785-8.[page needed]
- ^ “Model: Second-Order Exponential Smoothing”. SAP AG. Retrieved 23 January 2013.
- ^ “6.4.3.3. Double Exponential Smoothing”. itl.nist.gov. Retrieved 25 September 2011.
- ^ “Averaging and Exponential Smoothing Models”. duke.edu. Retrieved 25 September 2011.
- ^ Kalehar, Prajakta S. “Time series Forecasting using Holt–Winters Exponential Smoothing” (PDF). Retrieved 23 June 2014.
- ^ a b Winters, P. R. (April 1960). “Forecasting Sales by Exponentially Weighted Moving Averages”. Management Science. 6 (3): 324–342. doi:10.1287/mnsc.6.3.324.
- ^ “R: Holt–Winters Filtering”. stat.ethz.ch. Retrieved 5 June 2016.
- ^ “ets {forecast} | inside-R | A Community Site for R”. inside-r.org. Archived from the original on 16 July 2016. Retrieved 5 June 2016.
- ^ “Comparing HoltWinters() and ets()”. Hyndsight. 29 May 2011. Retrieved 5 June 2016.
- ^ tssmooth in Stata manual
- ^ “LibreOffice 5.2: Release Notes – the Document Foundation Wiki”.
- ^ “Excel 2016 Forecasting Functions | Real Statistics Using Excel”.
External links[edit]
- Lecture notes on exponential smoothing (Robert Nau, Duke University)
- Data Smoothing by Jon McLoone, The Wolfram Demonstrations Project
- The Holt–Winters Approach to Exponential Smoothing: 50 Years Old and Going Strong by Paul Goodwin (2010) Foresight: The International Journal of Applied Forecasting
- Algorithms for Unevenly Spaced Time Series: Moving Averages and Other Rolling Operators by Andreas Eckner
Доброго дня! Мы продолжаем наш цикл статей открытого курса по машинному обучению и сегодня поговорим о временных рядах.
 Посмотрим на то, как с ними работать в Python, какие возможные методы и модели можно использовать для прогнозирования; что такое двойное и тройное экспоненциальное взвешивание; что делать, если стационарность — это не про вас; как построить SARIMA и не умереть; и как прогнозировать xgboost-ом. И всё это будем применять к примеру из суровой реальности.
Посмотрим на то, как с ними работать в Python, какие возможные методы и модели можно использовать для прогнозирования; что такое двойное и тройное экспоненциальное взвешивание; что делать, если стационарность — это не про вас; как построить SARIMA и не умереть; и как прогнозировать xgboost-ом. И всё это будем применять к примеру из суровой реальности.
UPD 01.2022: С февраля 2022 г. ML-курс ODS на русском возрождается под руководством Петра Ермакова couatl. Для русскоязычной аудитории это предпочтительный вариант (c этими статьями на Хабре – в подкрепление), англоговорящим рекомендуется mlcourse.ai в режиме самостоятельного прохождения.
Видеозапись лекции по мотивам этой статьи в рамках второго запуска открытого курса (сентябрь-ноябрь 2017).
План этой статьи:
- Движемся, сглаживаем и оцениваем
- Rolling window estimations
- Экспоненциальное сглаживание, модель Хольта-Винтерса
- Кросс-валидация на временных рядах, подбор параметров
- Эконометрический подход
- Стационарность, единичные корни
- Избавляемся от нестационарности и строим SARIMA
- Линейные и не очень модели на временных рядах
- Извлечение признаков (Feature extraction)
- Линейная регрессия vs XGBoost
- Домашнее задание
- Полезные ресурсы
Введение
На работе я практически ежедневно сталкиваюсь с теми или иными задачами, связанными с временными рядам. Чаще всего возникает вопрос — а что у нас будет происходить с нашими показателями в ближайший день/неделю/месяц/пр. — сколько игроков установят приложения, сколько будет онлайна, как много действий совершат пользователи, и так далее. К задаче прогнозирования можно подходить по-разному, в зависимости от того, какого качества должен быть прогноз, на какой период мы хотим его строить, и, конечно, как долго нужно подбирать и настраивать параметры модели для его получения.
Начнем с простых методов анализа и прогнозирования — скользящих средних, сглаживаний и их вариаций.
Движемся, сглаживаем и оцениваем
Небольшое определение временного ряда:
Временной ряд – это последовательность значений, описывающих протекающий во времени процесс, измеренных в последовательные моменты времени, обычно через равные промежутки
Таким образом, данные оказываются упорядочены относительно неслучайных моментов времени, и, значит, в отличие от случайных выборок, могут содержать в себе дополнительную информацию, которую мы постараемся извлечь.
Импортируем нужные библиотеки. В основном нам понадобится модуль statsmodels, в котором реализованы многочисленные методы статистического моделирования, в том числе для временных рядов. Для поклонников R, пересевших на питон, он может показаться очень родным, так как поддерживает написание формулировок моделей в стиле ‘Wage ~ Age + Education’.
import sys
import warnings
warnings.filterwarnings('ignore')
from tqdm import tqdm
import pandas as pd
import numpy as np
from sklearn.metrics import mean_absolute_error, mean_squared_error
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
import statsmodels.api as sm
import scipy.stats as scs
from scipy.optimize import minimize
import matplotlib.pyplot as pltВ качестве примера для работы возьмем реальные данные по часовому онлайну игроков в одной из мобильных игрушек:
Код для отрисовки графика
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
from plotly import graph_objs as go
init_notebook_mode(connected = True)
def plotly_df(df, title = ''):
data = []
for column in df.columns:
trace = go.Scatter(
x = df.index,
y = df[column],
mode = 'lines',
name = column
)
data.append(trace)
layout = dict(title = title)
fig = dict(data = data, layout = layout)
iplot(fig, show_link=False)
dataset = pd.read_csv('hour_online.csv', index_col=['Time'], parse_dates=['Time'])
plotly_df(dataset, title = "Online users")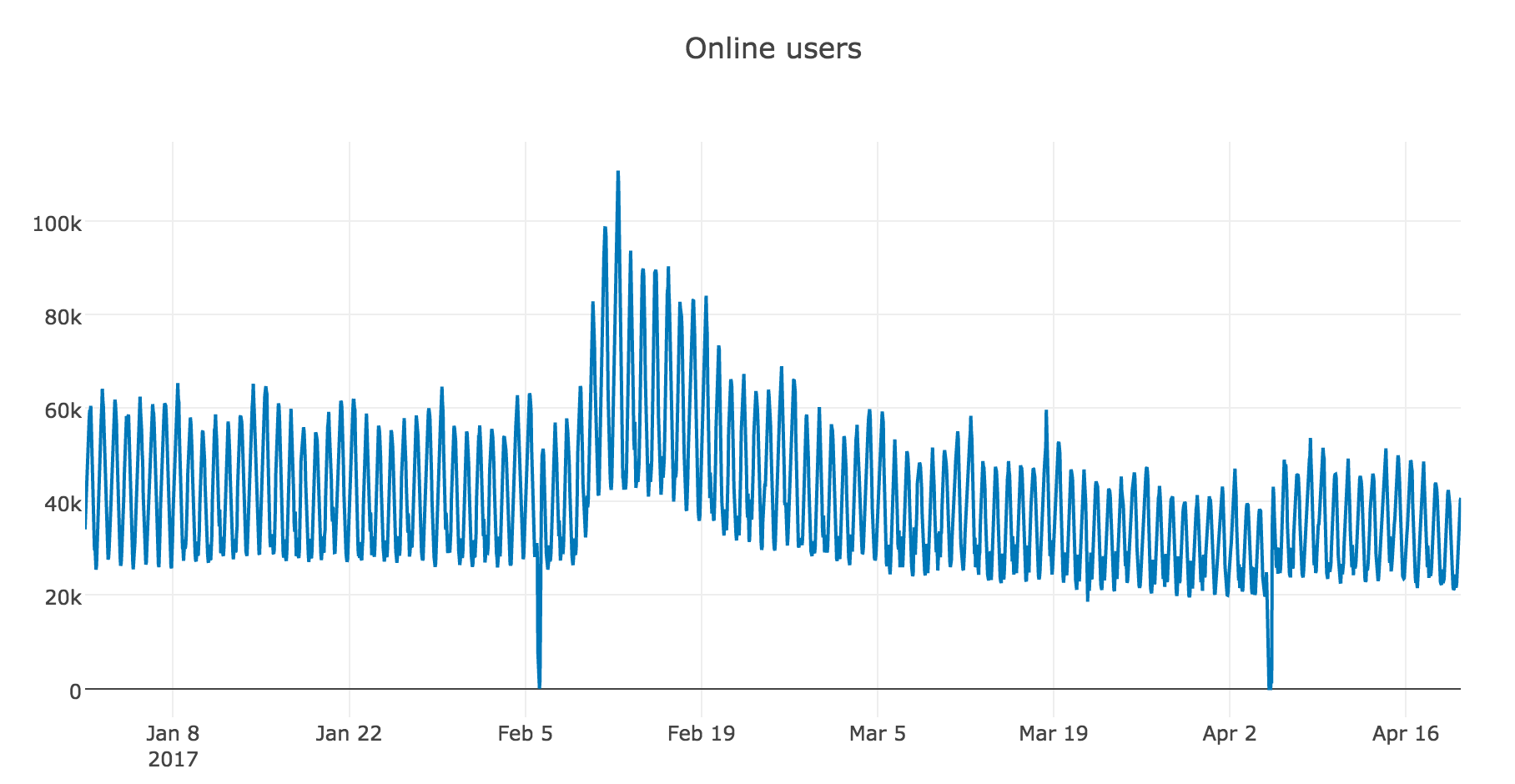
Rolling window estimations
Начнем моделирование с наивного предположения — “завтра будет, как вчера”, но вместо модели вида будем считать, что будущее значение переменной зависит от среднего
её предыдущих значений, а значит, воспользуемся скользящей средней.
Реализуем эту же функцию в питоне и посмотрим на прогноз, построенный по последнему наблюдаемому дню (24 часа)
def moving_average(series, n):
return np.average(series[-n:])
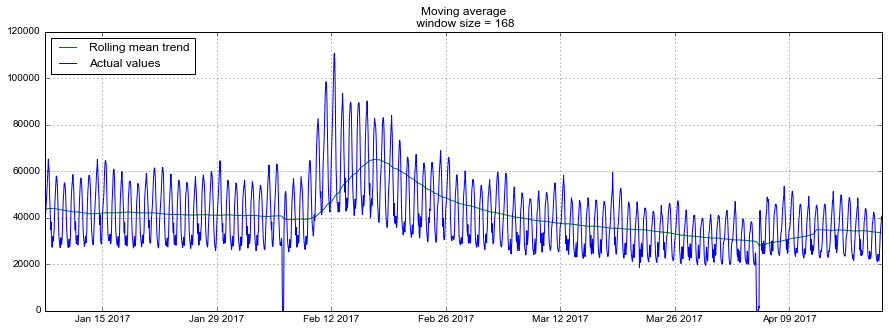
moving_average(dataset.Users, 24)Out: 29858.333333333332К сожалению, такой прогноз долгосрочным сделать не удастся — для получения предсказания на шаг вперед предыдущее значение должно быть фактически наблюдаемой величиной. Зато у скользящей средней есть другое применение — сглаживание исходного ряда для выявления трендов. В пандасе есть готовая реализация — DataFrame.rolling(window).mean(). Чем больше зададим ширину интервала — тем более сглаженным окажется тренд. В случае, если данные сильно зашумлены, что особенно часто встречается, например, в финансовых показателях, такая процедура может помочь с определением общих паттернов.
Для нашего ряда тренды и так вполне очевидны, но если сгладить по дням, становится лучше видна динамика онлайна по будням и выходным (выходные — время поиграть), а недельное сглаживание хорошо отражает общие изменения, связанные с резким ростом числа активных игроков в феврале и последующим снижением в марте.
Код для отрисовки графика
def plotMovingAverage(series, n):
"""
series - dataframe with timeseries
n - rolling window size
"""
rolling_mean = series.rolling(window=n).mean()
# При желании, можно строить и доверительные интервалы для сглаженных значений
#rolling_std = series.rolling(window=n).std()
#upper_bond = rolling_mean+1.96*rolling_std
#lower_bond = rolling_mean-1.96*rolling_std
plt.figure(figsize=(15,5))
plt.title("Moving averagen window size = {}".format(n))
plt.plot(rolling_mean, "g", label="Rolling mean trend")
#plt.plot(upper_bond, "r--", label="Upper Bond / Lower Bond")
#plt.plot(lower_bond, "r--")
plt.plot(dataset[n:], label="Actual values")
plt.legend(loc="upper left")
plt.grid(True)plotMovingAverage(dataset, 24) # сглаживаем по дням
plotMovingAverage(dataset, 24*7) # сглаживаем по неделям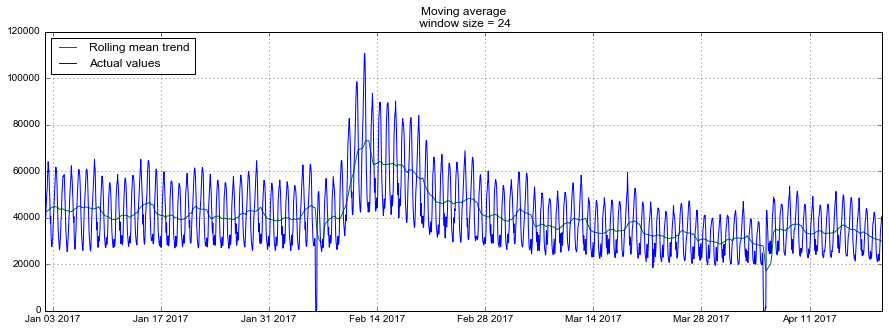
Модификацией простой скользящей средней является взвешенная средняя, внутри которой наблюдениям придаются различные веса, в сумме дающие единицу, при этом обычно последним наблюдениям присваивается больший вес.
def weighted_average(series, weights):
result = 0.0
weights.reverse()
for n in range(len(weights)):
result += series[-n-1] * weights[n]
return result
weighted_average(dataset.Users, [0.6, 0.2, 0.1, 0.07, 0.03])Out: 35967.550000000003Экспоненциальное сглаживание, модель Хольта-Винтерса
Простое экспоненциальное сглаживание
А теперь посмотрим, что произойдёт, если вместо взвешивания последних значений ряда мы начнем взвешивать все доступные наблюдения, при этом экспоненциально уменьшая веса по мере углубления в исторические данные. В этом нам поможет формула простого экспоненциального сглаживания:
Здесь модельное значение представляет собой средневзвешенную между текущим истинным и предыдущим модельным значениями. Вес называется сглаживающим фактором. Он определяет, как быстро мы будем “забывать” последнее доступное истинное наблюдение. Чем меньше
, тем больше влияния оказывают предыдущие модельные значения, и тем сильнее сглаживается ряд.
Экспоненциальность скрывается в рекурсивности функции — каждый раз мы умножаем на предыдущее модельное значение, которое, в свою очередь, также содержало в себе
, и так до самого начала.
def exponential_smoothing(series, alpha):
result = [series[0]] # first value is same as series
for n in range(1, len(series)):
result.append(alpha * series[n] + (1 - alpha) * result[n-1])
return resultКод для отрисовки графика
with plt.style.context('seaborn-white'):
plt.figure(figsize=(20, 8))
for alpha in [0.3, 0.05]:
plt.plot(exponential_smoothing(dataset.Users, alpha), label="Alpha {}".format(alpha))
plt.plot(dataset.Users.values, "c", label = "Actual")
plt.legend(loc="best")
plt.axis('tight')
plt.title("Exponential Smoothing")
plt.grid(True)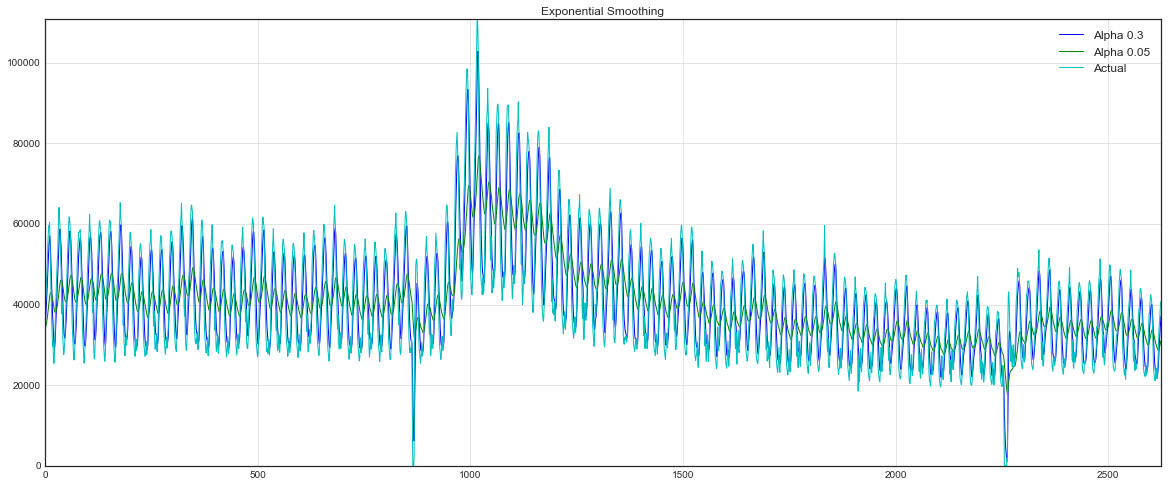
Двойное экспоненциальное сглаживание
До сих пор мы могли получить от наших методов в лучшем случае прогноз лишь на одну точку вперёд (и ещё красиво сгладить ряд), это здорово, но недостаточно, поэтому переходим к расширению экспоненциального сглаживания, которое позволит строить прогноз сразу на две точки вперед (и тоже красиво сглаживать ряд).
В этом нам поможет разбиение ряда на две составляющие — уровень (level, intercept) и тренд
(trend, slope). Уровень, или ожидаемое значение ряда, мы предсказывали при помощи предыдущих методов, а теперь такое же экспоненциальное сглаживание применим к тренду, наивно или не очень полагая, что будущее направление изменения ряда зависит от взвешенных предыдущих изменений.
В результате получаем набор функций. Первая описывает уровень — он, как и прежде, зависит от текущего значения ряда, а второе слагаемое теперь разбивается на предыдущее значение уровня и тренда. Вторая отвечает за тренд — он зависит от изменения уровня на текущем шаге, и от предыдущего значения тренда. Здесь в роли веса в экспоненциальном сглаживании выступает коэффициент . Наконец, итоговое предсказание представляет собой сумму модельных значений уровня и тренда.
def double_exponential_smoothing(series, alpha, beta):
result = [series[0]]
for n in range(1, len(series)+1):
if n == 1:
level, trend = series[0], series[1] - series[0]
if n >= len(series): # прогнозируем
value = result[-1]
else:
value = series[n]
last_level, level = level, alpha*value + (1-alpha)*(level+trend)
trend = beta*(level-last_level) + (1-beta)*trend
result.append(level+trend)
return resultКод для отрисовки графика
with plt.style.context('seaborn-white'):
plt.figure(figsize=(20, 8))
for alpha in [0.9, 0.02]:
for beta in [0.9, 0.02]:
plt.plot(double_exponential_smoothing(dataset.Users, alpha, beta), label="Alpha {}, beta {}".format(alpha, beta))
plt.plot(dataset.Users.values, label = "Actual")
plt.legend(loc="best")
plt.axis('tight')
plt.title("Double Exponential Smoothing")
plt.grid(True)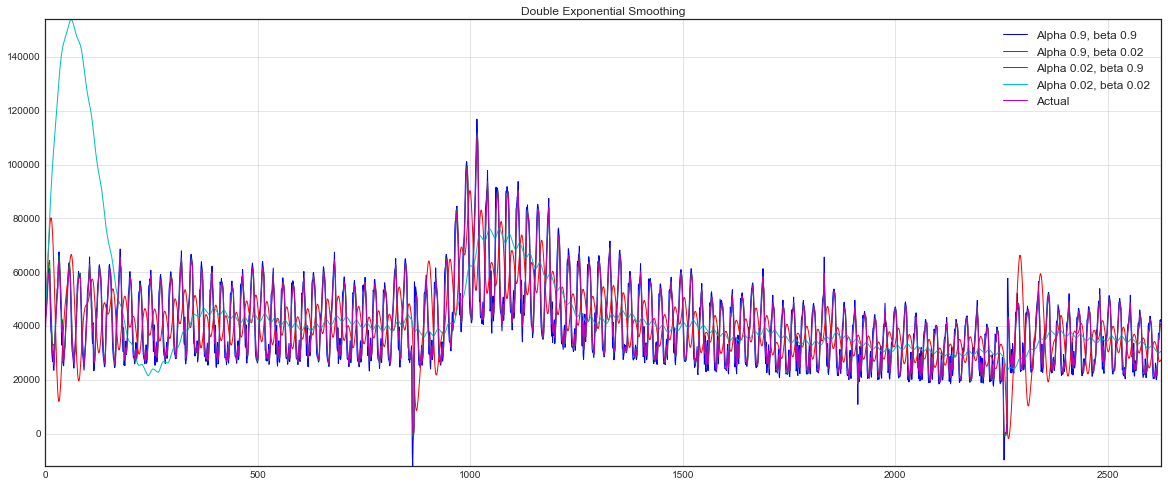
Теперь настраивать пришлось уже два параметра — и
. Первый отвечает за сглаживание ряда вокруг тренда, второй — за сглаживание самого тренда. Чем выше значения, тем больший вес будет отдаваться последним наблюдениям и тем менее сглаженным окажется модельный ряд. Комбинации параметров могут выдавать достаточно причудливые результаты, особенно если задавать их руками. А о не ручном подборе параметров расскажу чуть ниже, сразу после тройного экспоненциального сглаживания.
Тройное экспоненциальное сглаживание a.k.a. Holt-Winters
Итак, успешно добрались до следующего варианта экспоненциального сглаживания, на сей раз тройного.
Идея этого метода заключается в добавлении еще одной, третьей, компоненты — сезонности. Соответственно, метод применим только в случае, если ряд этой сезонностью не обделён, что в нашем случае верно. Сезонная компонента в модели будет объяснять повторяющиеся колебания вокруг уровня и тренда, а характеризоваться она будет длиной сезона — периодом, после которого начинаются повторения колебаний. Для каждого наблюдения в сезоне формируется своя компонента, например, если длина сезона составляет 7 (например, недельная сезонность), то получим 7 сезонных компонент, по штуке на каждый из дней недели.
Получаем новую систему:
Уровень теперь зависит от текущего значения ряда за вычетом соответствующей сезонной компоненты, тренд остаётся без изменений, а сезонная компонента зависит от текущего значения ряда за вычетом уровня и от предыдущего значения компоненты. При этом компоненты сглаживаются через все доступные сезоны, например, если это компонента, отвечающая за понедельник, то и усредняться она будет только с другими понедельниками. Подробнее про работу усреднений и оценку начальных значений тренда и сезонных компонент можно почитать здесь. Теперь, имея сезонную компоненту, мы можем предсказывать уже не на один, и даже не на два, а на произвольные шагов вперёд, что не может не радовать.
Ниже приведен код для построения модели тройного экспоненциального сглаживания, также известного по фамилиям её создателей — Чарльза Хольта и его студента Питера Винтерса.
Дополнительно в модель включен метод Брутлага для построения доверительных интервалов:
где — длина сезона,
— предсказанное отклонение, а остальные параметры берутся из тройного сглаживани. Подробнее о методе и о его применении к поиску аномалий во временных рядах можно прочесть здесь
Код для модели Хольта-Винтерса
class HoltWinters:
"""
Модель Хольта-Винтерса с методом Брутлага для детектирования аномалий
https://fedcsis.org/proceedings/2012/pliks/118.pdf
# series - исходный временной ряд
# slen - длина сезона
# alpha, beta, gamma - коэффициенты модели Хольта-Винтерса
# n_preds - горизонт предсказаний
# scaling_factor - задаёт ширину доверительного интервала по Брутлагу (обычно принимает значения от 2 до 3)
"""
def __init__(self, series, slen, alpha, beta, gamma, n_preds, scaling_factor=1.96):
self.series = series
self.slen = slen
self.alpha = alpha
self.beta = beta
self.gamma = gamma
self.n_preds = n_preds
self.scaling_factor = scaling_factor
def initial_trend(self):
sum = 0.0
for i in range(self.slen):
sum += float(self.series[i+self.slen] - self.series[i]) / self.slen
return sum / self.slen
def initial_seasonal_components(self):
seasonals = {}
season_averages = []
n_seasons = int(len(self.series)/self.slen)
# вычисляем сезонные средние
for j in range(n_seasons):
season_averages.append(sum(self.series[self.slen*j:self.slen*j+self.slen])/float(self.slen))
# вычисляем начальные значения
for i in range(self.slen):
sum_of_vals_over_avg = 0.0
for j in range(n_seasons):
sum_of_vals_over_avg += self.series[self.slen*j+i]-season_averages[j]
seasonals[i] = sum_of_vals_over_avg/n_seasons
return seasonals
def triple_exponential_smoothing(self):
self.result = []
self.Smooth = []
self.Season = []
self.Trend = []
self.PredictedDeviation = []
self.UpperBond = []
self.LowerBond = []
seasonals = self.initial_seasonal_components()
for i in range(len(self.series)+self.n_preds):
if i == 0: # инициализируем значения компонент
smooth = self.series[0]
trend = self.initial_trend()
self.result.append(self.series[0])
self.Smooth.append(smooth)
self.Trend.append(trend)
self.Season.append(seasonals[i%self.slen])
self.PredictedDeviation.append(0)
self.UpperBond.append(self.result[0] +
self.scaling_factor *
self.PredictedDeviation[0])
self.LowerBond.append(self.result[0] -
self.scaling_factor *
self.PredictedDeviation[0])
continue
if i >= len(self.series): # прогнозируем
m = i - len(self.series) + 1
self.result.append((smooth + m*trend) + seasonals[i%self.slen])
# во время прогноза с каждым шагом увеличиваем неопределенность
self.PredictedDeviation.append(self.PredictedDeviation[-1]*1.01)
else:
val = self.series[i]
last_smooth, smooth = smooth, self.alpha*(val-seasonals[i%self.slen]) + (1-self.alpha)*(smooth+trend)
trend = self.beta * (smooth-last_smooth) + (1-self.beta)*trend
seasonals[i%self.slen] = self.gamma*(val-smooth) + (1-self.gamma)*seasonals[i%self.slen]
self.result.append(smooth+trend+seasonals[i%self.slen])
# Отклонение рассчитывается в соответствии с алгоритмом Брутлага
self.PredictedDeviation.append(self.gamma * np.abs(self.series[i] - self.result[i])
+ (1-self.gamma)*self.PredictedDeviation[-1])
self.UpperBond.append(self.result[-1] +
self.scaling_factor *
self.PredictedDeviation[-1])
self.LowerBond.append(self.result[-1] -
self.scaling_factor *
self.PredictedDeviation[-1])
self.Smooth.append(smooth)
self.Trend.append(trend)
self.Season.append(seasonals[i % self.slen])Кросс-валидация на временных рядах, подбор параметров
Перед тем, как построить модель, поговорим, наконец, о не ручной оценке параметров для моделей.
Ничего необычного здесь нет, по-прежнему сначала необходимо выбрать подходящуюю для данной задачи функцию потерь: RMSE, MAE, MAPE и др., которая будет следить за качеством подгонки модели под исходные данные. Затем будем оценивать на кросс-валидации значение функции потерь при данных параметрах модели, искать градиент, менять в соответствии с ним параметры и бодро опускаться в сторону глобального минимума ошибки.
Небольшая загвоздка возникает только в кросс-валидации. Проблема состоит в том, что временной ряд имеет, как ни парадоксально, временную структуру, и случайно перемешивать в фолдах значения всего ряда без сохранения этой структуры нельзя, иначе в процессе потеряются все взаимосвязи наблюдений друг с другом. Поэтому придется использовать чуть более хитрый способ для оптимизации параметров, официального названия которому я так и не нашел, но на сайте CrossValidated, где можно найти ответы на всё, кроме главного вопроса Жизни, Вселенной и Всего Остального, предлагают название “cross-validation on a rolling basis”, что не дословно можно перевести как кросс-валидация на скользящем окне.
Суть достаточно проста — начинаем обучать модель на небольшом отрезке временного ряда, от начала до некоторого , делаем прогноз на
шагов вперед и считаем ошибку. Далее расширяем обучающую выборку до
значения и прогнозируем с
до
, так продолжаем двигать тестовый отрезок ряда до тех пор, пока не упрёмся в последнее доступное наблюдение. В итоге получим столько фолдов, сколько
уместится в промежуток между изначальным обучающим отрезком и всей длиной ряда.
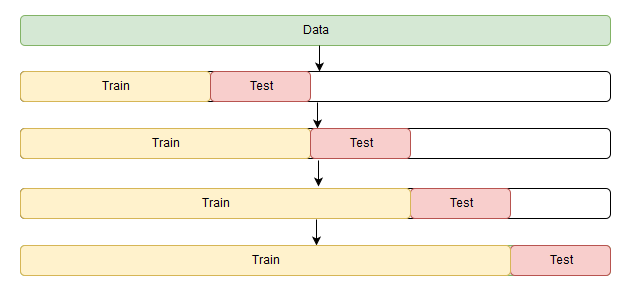
Код для кросс-валидации на временном ряду
from sklearn.model_selection import TimeSeriesSplit
def timeseriesCVscore(x):
# вектор ошибок
errors = []
values = data.values
alpha, beta, gamma = x
# задаём число фолдов для кросс-валидации
tscv = TimeSeriesSplit(n_splits=3)
# идем по фолдам, на каждом обучаем модель, строим прогноз на отложенной выборке и считаем ошибку
for train, test in tscv.split(values):
model = HoltWinters(series=values[train], slen = 24*7, alpha=alpha, beta=beta, gamma=gamma, n_preds=len(test))
model.triple_exponential_smoothing()
predictions = model.result[-len(test):]
actual = values[test]
error = mean_squared_error(predictions, actual)
errors.append(error)
# Возвращаем средний квадрат ошибки по вектору ошибок
return np.mean(np.array(errors))Значение длины сезона 24*7 возникло не случайно — в исходном ряде отчетливо видна дневная сезонность, (отсюда 24), и недельная — по будням ниже, на выходных — выше, (отсюда 7), суммарно сезонных компонент получится 24*7.
В модели Хольта-Винтерса, как и в остальных моделях экспоненциального сглаживания, есть ограничение на величину сглаживающих параметров — каждый из них может принимать значения от 0 до 1, поэтому для минимизации функции потерь нужно выбирать алгоритм, поддерживающий ограничения на параметры, в данном случае — Truncated Newton conjugate gradient.
%%time
data = dataset.Users[:-500] # отложим часть данных для тестирования
# инициализируем значения параметров
x = [0, 0, 0]
# Минимизируем функцию потерь с ограничениями на параметры
opt = minimize(timeseriesCVscore, x0=x, method="TNC", bounds = ((0, 1), (0, 1), (0, 1)))
# Из оптимизатора берем оптимальное значение параметров
alpha_final, beta_final, gamma_final = opt.x
print(alpha_final, beta_final, gamma_final)Out: (0.0066342670643441681, 0.0, 0.046765204289672901)Передадим полученные оптимальные значения коэффициентов ,
и
и построим прогноз на 5 дней вперёд (128 часов)
# Передаем оптимальные значения модели,
data = dataset.Users
model = HoltWinters(data[:-128], slen = 24*7, alpha = alpha_final, beta = beta_final, gamma = gamma_final, n_preds = 128, scaling_factor = 2.56)
model.triple_exponential_smoothing()Код для отрисовки графика
def plotHoltWinters():
Anomalies = np.array([np.NaN]*len(data))
Anomalies[data.values<model.LowerBond] = data.values[data.values<model.LowerBond]
plt.figure(figsize=(25, 10))
plt.plot(model.result, label = "Model")
plt.plot(model.UpperBond, "r--", alpha=0.5, label = "Up/Low confidence")
plt.plot(model.LowerBond, "r--", alpha=0.5)
plt.fill_between(x=range(0,len(model.result)), y1=model.UpperBond, y2=model.LowerBond, alpha=0.5, color = "grey")
plt.plot(data.values, label = "Actual")
plt.plot(Anomalies, "o", markersize=10, label = "Anomalies")
plt.axvspan(len(data)-128, len(data), alpha=0.5, color='lightgrey')
plt.grid(True)
plt.axis('tight')
plt.legend(loc="best", fontsize=13);
plotHoltWinters()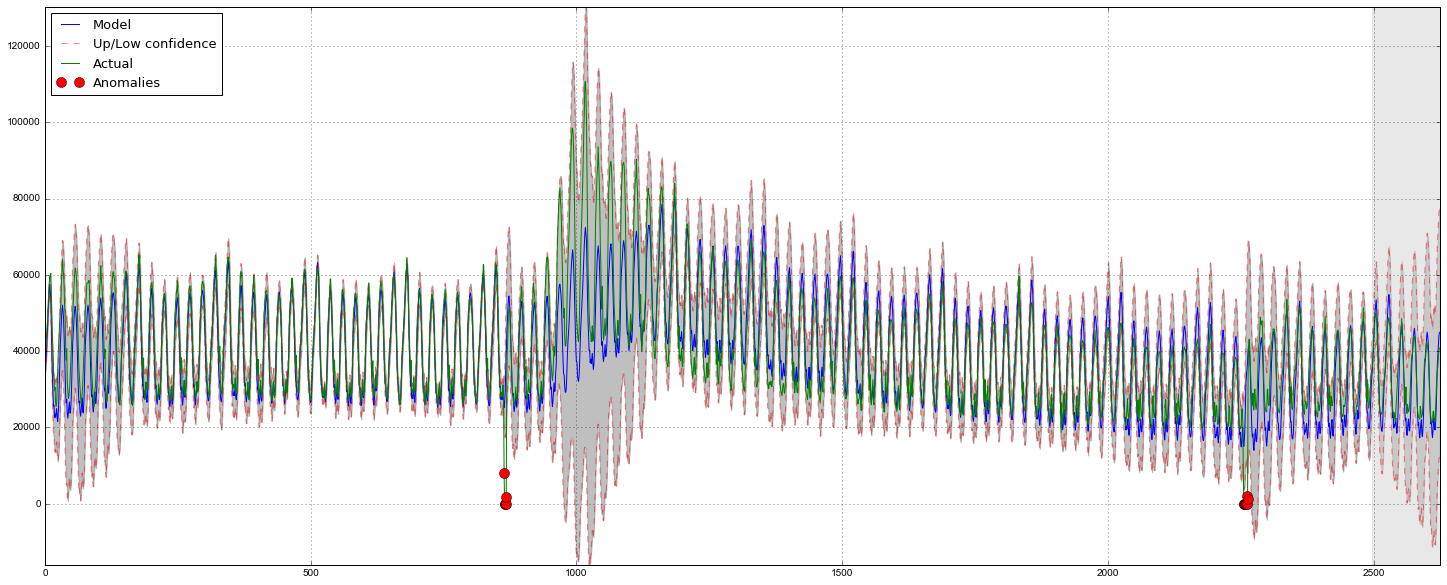
Судя по графику, модель неплохо описала исходный временной ряд, уловив недельную и дневную сезонность, и даже смогла поймать аномальные снижения, вышедшие за пределы доверительных интервалов. Если посмотреть на смоделированное отклонение, хорошо видно, что модель достаточно резко регирует на значительные изменения в структуре ряда, но при этом быстро возвращает дисперсию к обычным значениям, “забывая” прошлое. Такая особенность позволяет неплохо и без значительных затрат на подготовку-обучение модели настроить систему по детектированию аномалий даже в достаточно шумных рядах.
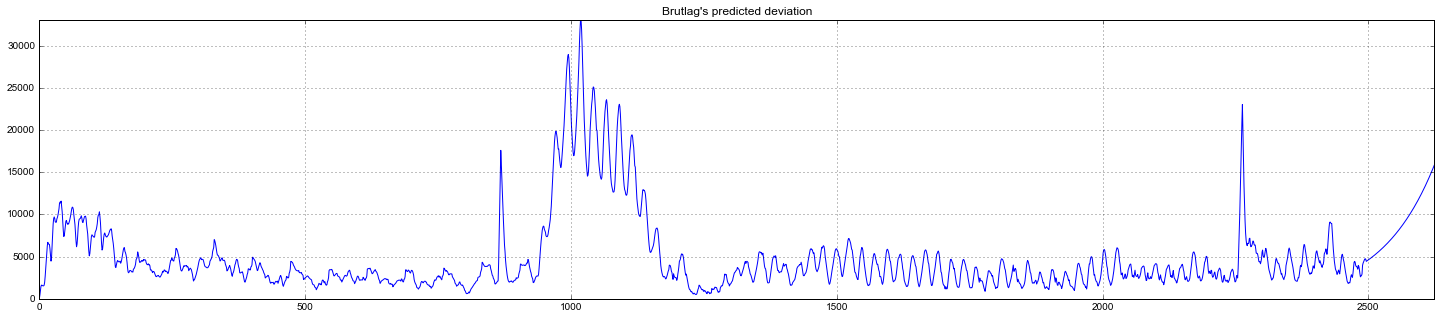
Эконометрический подход
Стационарность, единичные корни
Перед тем, как перейти к моделированию, стоит сказать о таком важном свойстве временного ряда, как стационарность.
Под стационарностью понимают свойство процесса не менять своих статистических характеристик с течением времени, а именно постоянство матожидания, постоянство дисперсии (она же гомоскедастичность) и независимость ковариационной функции от времени (должна зависеть только от расстояния между наблюдениями). Наглядно можно посмотреть на эти свойства на картинках, взятых из поста Sean Abu:
- Временной ряд справа не является стационарным, так как его матожидание со временем растёт
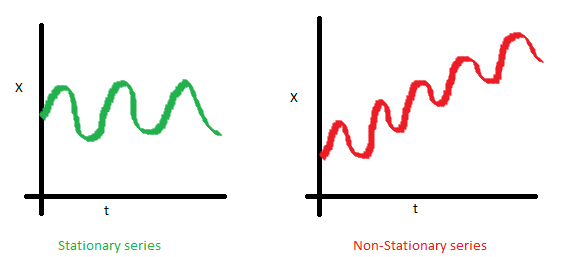
- Здесь не повезло с дисперсией — разброс значений ряда существенно варьируется в зависимости от периода
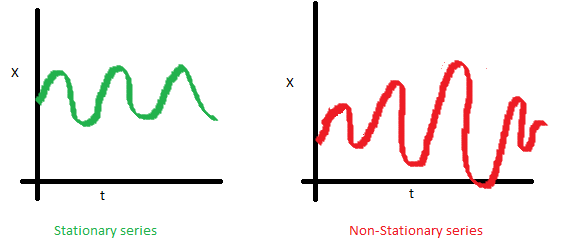
- Наконец, на последнем графике видно, что значения ряда внезапно становятся ближе друг ко другу, образуя некоторый кластер, а в результате получаем непостоянство ковариаций
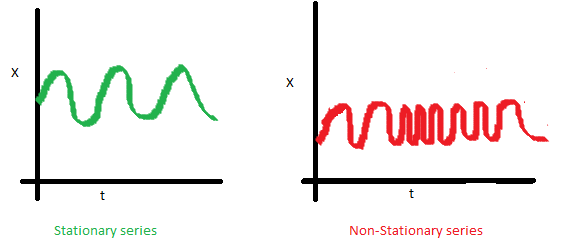
Почему стационарность так важна? По стационарному ряду просто строить прогноз, так как мы полагаем, что его будущие статистические характеристики не будут отличаться от наблюдаемых текущих. Большинство моделей временных рядов так или иначе моделируют и предсказывают эти характеристики (например, матожидание или дисперсию), поэтому в случае нестационарности исходного ряда предсказания окажутся неверными. К сожалению, большинство временных рядов, с которыми приходится сталкиваться за пределыми учебных материалов, стационарными не являются, но с этим можно (и нужно) бороться.
Чтобы бороться с нестационарностью, нужно узнать её в лицо, потому посмотрим, как её детектировать. Для этого обратимся к белому шуму и случайному блужданию, чтобы выяснить как попасть из одного в другое бесплатно и без смс.
График белого шума:
white_noise = np.random.normal(size=1000)
with plt.style.context('bmh'):
plt.figure(figsize=(15, 5))
plt.plot(white_noise)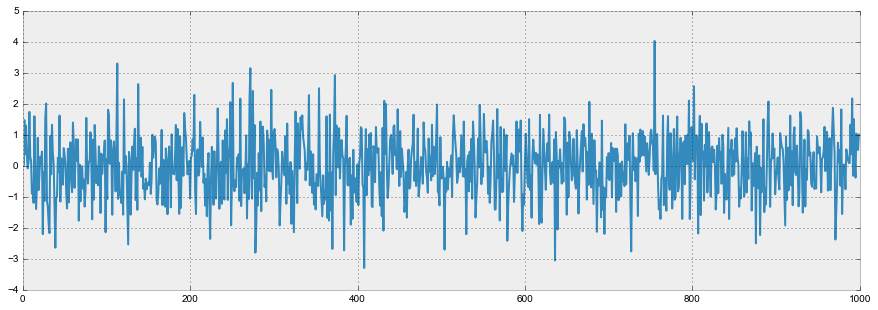
Итак, процесс, порожденный стандартным нормальным распределением, стационарен, колеблется вокруг нуля с отклонением в 1. Теперь на основании него сгенерируем новый процесс, в котором каждое последующее значение будет зависеть от предыдущего:
Код для отрисовки графиков
def plotProcess(n_samples=1000, rho=0):
x = w = np.random.normal(size=n_samples)
for t in range(n_samples):
x[t] = rho * x[t-1] + w[t]
with plt.style.context('bmh'):
plt.figure(figsize=(10, 3))
plt.plot(x)
plt.title("Rho {}n Dickey-Fuller p-value: {}".format(rho, round(sm.tsa.stattools.adfuller(x)[1], 3)))
for rho in [0, 0.6, 0.9, 1]:
plotProcess(rho=rho)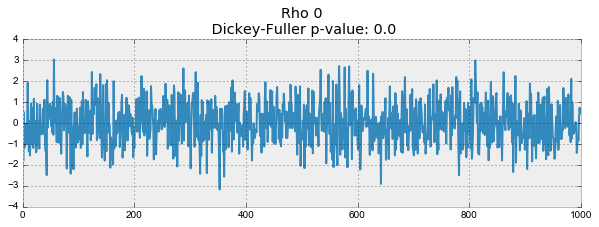
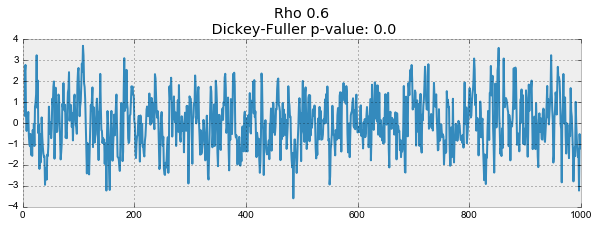
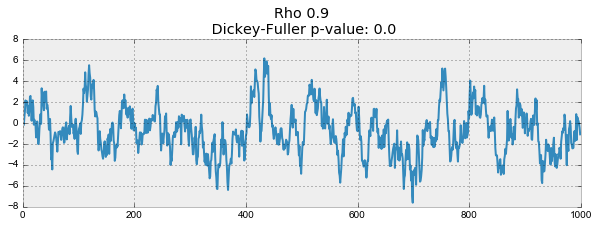
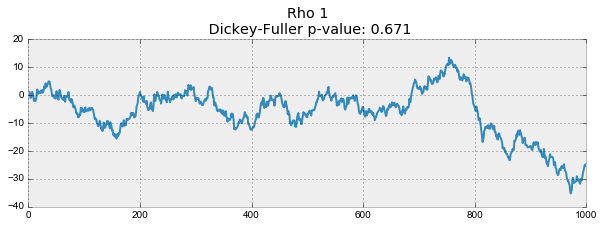
На первом графике получился точно такой же стационарный белый шум, который строился раньше. На втором значение увеличилось до 0.6, в результате чего на графике стали появляться более широкие циклы, но в целом стационарным он быть пока не перестал. Третий график всё сильнее отклоняется от нулевого среднего значения, но всё ещё колеблется вокруг него. Наконец, значение
равное единице дало процесс случайного блуждания — ряд не стационарен.
Происходит это из-за того, что при достижении критической единицы, ряд перестаёт возвращаться к своему среднему значению. Если вычесть из левой и правой части
, то получим
, где выражение слева — первые разности. Если
, то первые разности дадут стационарный белый шум
. Этот факт лёг в основу теста Дики-Фуллера на стационарность ряда (наличие единичного корня). Если из нестационарного ряда первыми разностями удаётся получить стационарный, то он называется интегрированным первого порядка. Нулевая гипотеза теста — ряд не стационарен, отвергалась на первых трех графиках, и принялась на последнем. Стоит сказать, что не всегда для получения стационарного ряда хватает первых разностей, так как процесс может быть интегрированным с более высоким порядком (иметь несколько единичных корней), для проверки таких случаев используют расширенный тест Дики-Фуллера, проверяющий сразу несколько лагов.
Бороться с нестационарностью можно множеством способов — разностями различного порядка, выделением тренда и сезонности, сглаживаниями и преобразованиями, например, Бокса-Кокса или логарифмированием.
Избавляемся от нестационарности и строим SARIMA
Попробуем теперь построить ARIMA модель для онлайна игроков, пройдя все круги ада стадии приведения ряда к стационарному виду. Про саму модель уже не раз писали на хабре — Построение модели SARIMA с помощью Python+R, Анализ временных рядов с помощью python, поэтому подробно останавливаться на ней не буду.
Код для отрисовки графиков
def tsplot(y, lags=None, figsize=(12, 7), style='bmh'):
if not isinstance(y, pd.Series):
y = pd.Series(y)
with plt.style.context(style):
fig = plt.figure(figsize=figsize)
layout = (2, 2)
ts_ax = plt.subplot2grid(layout, (0, 0), colspan=2)
acf_ax = plt.subplot2grid(layout, (1, 0))
pacf_ax = plt.subplot2grid(layout, (1, 1))
y.plot(ax=ts_ax)
ts_ax.set_title('Time Series Analysis Plots')
smt.graphics.plot_acf(y, lags=lags, ax=acf_ax, alpha=0.5)
smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax, alpha=0.5)
print("Критерий Дики-Фуллера: p=%f" % sm.tsa.stattools.adfuller(y)[1])
plt.tight_layout()
return
tsplot(dataset.Users, lags=30)Out: Критерий Дики-Фуллера: p=0.190189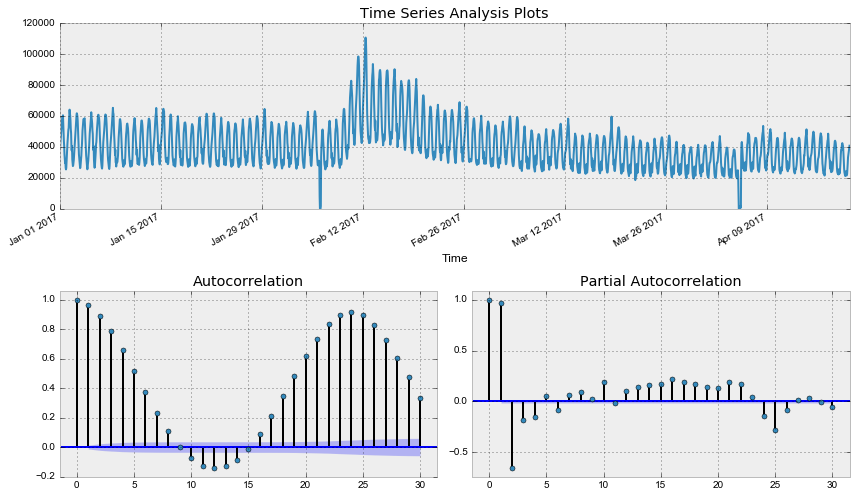
Как и следовало ожидать, исходный ряд стационарным не является, критерий Дики-Фуллера не отверг нулевую гипотезу о наличии единичного корня. Попробуем стабилизировать дисперсию преоразованием Бокса-Кокса.
def invboxcox(y,lmbda):
# обрабтное преобразование Бокса-Кокса
if lmbda == 0:
return(np.exp(y))
else:
return(np.exp(np.log(lmbda*y+1)/lmbda))
data = dataset.copy()
data['Users_box'], lmbda = scs.boxcox(data.Users+1) # прибавляем единицу, так как в исходном ряде есть нули
tsplot(data.Users_box, lags=30)
print("Оптимальный параметр преобразования Бокса-Кокса: %f" % lmbda)Out: Критерий Дики-Фуллера: p=0.079760
Оптимальный параметр преобразования Бокса-Кокса: 0.587270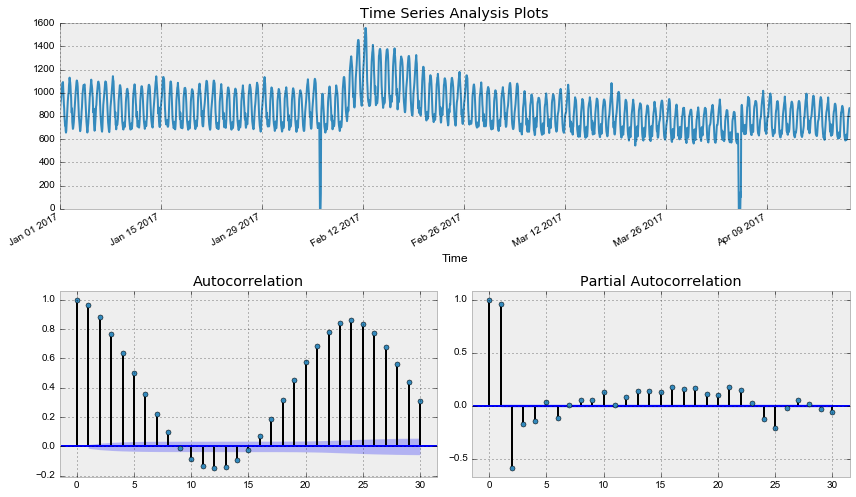
Уже лучше, однако критерий Дики-Фуллера по-прежнему не отвергает гипотезу о нестационарности ряда. А автокорреляционная функция явно намекает на сезонность в получившемся ряде. Возьмём сезонные разности:
data['Users_box_season'] = data.Users_box - data.Users_box.shift(24*7)
tsplot(data.Users_box_season[24*7:], lags=30)Out: Критерий Дики-Фуллера: p=0.002571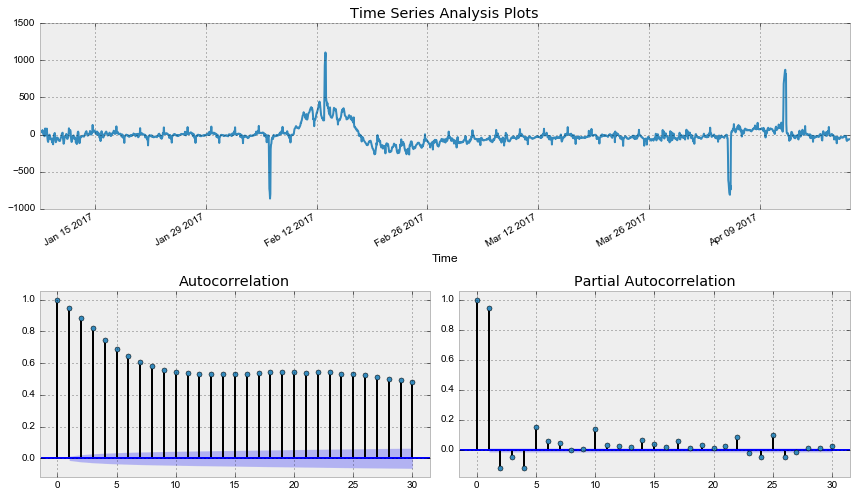
Критерий Дики-Фуллера теперь отвергает нулевую гипотезу о нестационарности, но автокорреляционная функция всё ещё выглядит нехорошо из-за большого числа значимых лагов. Так как на графике частной автокорреляционной функции значим лишь один лаг, стоит взять еще первые разности, чтобы привести наконец ряд к стационарному виду.
data['Users_box_season_diff'] = data.Users_box_season - data.Users_box_season.shift(1)
tsplot(data.Users_box_season_diff[24*7+1:], lags=30)Out: Критерий Дики-Фуллера: p=0.000000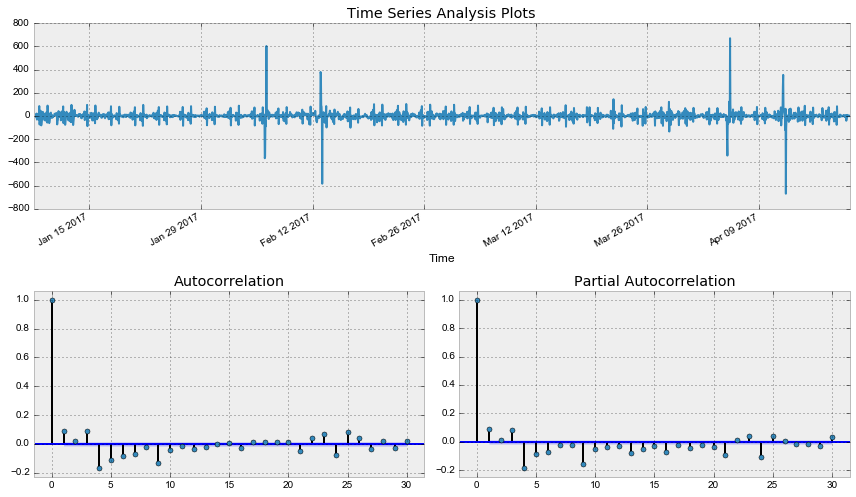
Наконец, получили стационарный ряд, по автокорреляционной и частной автокорреляционной функции прикинем параметры для SARIMA модели, на забыв, что предварительно уже сделали первые и сезонные разности.
Начальные приближения Q = 1, P = 4, q = 3, p = 4
ps = range(0, 5)
d=1
qs = range(0, 4)
Ps = range(0, 5)
D=1
Qs = range(0, 1)
from itertools import product
parameters = product(ps, qs, Ps, Qs)
parameters_list = list(parameters)
len(parameters_list)Out: 100Код для подбора параметров перебором
%%time
results = []
best_aic = float("inf")
for param in tqdm(parameters_list):
#try except нужен, потому что на некоторых наборах параметров модель не обучается
try:
model=sm.tsa.statespace.SARIMAX(data.Users_box, order=(param[0], d, param[1]),
seasonal_order=(param[2], D, param[3], 24*7)).fit(disp=-1)
#выводим параметры, на которых модель не обучается и переходим к следующему набору
except ValueError:
print('wrong parameters:', param)
continue
aic = model.aic
#сохраняем лучшую модель, aic, параметры
if aic < best_aic:
best_model = model
best_aic = aic
best_param = param
results.append([param, model.aic])
warnings.filterwarnings('default')
result_table = pd.DataFrame(results)
result_table.columns = ['parameters', 'aic']
print(result_table.sort_values(by = 'aic', ascending=True).head())Лучшие параметры загоняем в модель:
%%time
best_model = sm.tsa.statespace.SARIMAX(data.Users_box, order=(4, d, 3),
seasonal_order=(4, D, 1, 24)).fit(disp=-1)
print(best_model.summary()) Statespace Model Results
==========================================================================================
Dep. Variable: Users_box No. Observations: 2625
Model: SARIMAX(4, 1, 3)x(4, 1, 1, 24) Log Likelihood -12547.157
Date: Sun, 23 Apr 2017 AIC 25120.315
Time: 02:06:39 BIC 25196.662
Sample: 0 HQIC 25147.964
- 2625
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.6794 0.108 6.310 0.000 0.468 0.890
ar.L2 -0.0810 0.181 -0.448 0.654 -0.435 0.273
ar.L3 0.3255 0.137 2.371 0.018 0.056 0.595
ar.L4 -0.2154 0.028 -7.693 0.000 -0.270 -0.161
ma.L1 -0.5086 0.106 -4.784 0.000 -0.717 -0.300
ma.L2 -0.0673 0.170 -0.395 0.693 -0.401 0.267
ma.L3 -0.3490 0.117 -2.976 0.003 -0.579 -0.119
ar.S.L24 0.1023 0.012 8.377 0.000 0.078 0.126
ar.S.L48 -0.0686 0.021 -3.219 0.001 -0.110 -0.027
ar.S.L72 0.1971 0.009 21.573 0.000 0.179 0.215
ar.S.L96 -0.1217 0.013 -9.279 0.000 -0.147 -0.096
ma.S.L24 -0.9983 0.045 -22.085 0.000 -1.087 -0.910
sigma2 873.4159 36.206 24.124 0.000 802.454 944.378
===================================================================================
Ljung-Box (Q): 130.47 Jarque-Bera (JB): 1194707.99
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 1.40 Skew: 2.65
Prob(H) (two-sided): 0.00 Kurtosis: 107.88
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).Проверим остатки модели:
tsplot(best_model.resid[24:], lags=30)Out: Критерий Дики-Фуллера: p=0.000000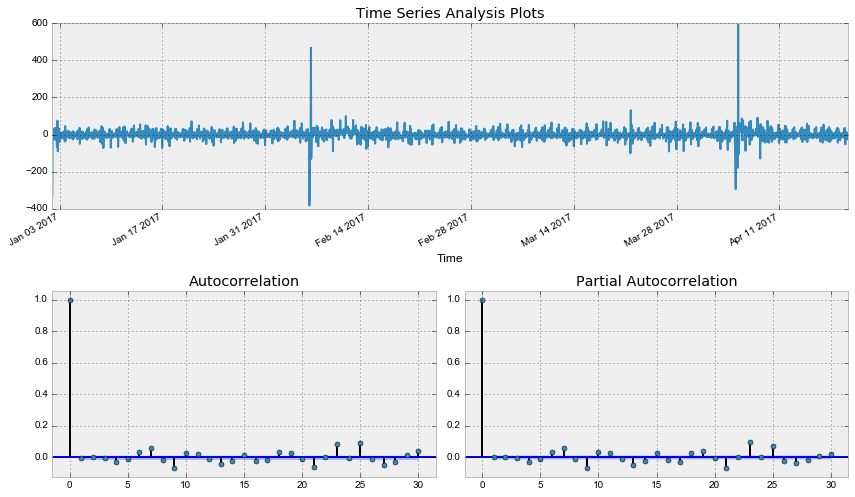
Что ж, остатки стационарны, явных автокорреляций нет, построим прогноз по получившейся модели
Код для построения прогноза и отрисовки графика
data["arima_model"] = invboxcox(best_model.fittedvalues, lmbda)
forecast = invboxcox(best_model.predict(start = data.shape[0], end = data.shape[0]+100), lmbda)
forecast = data.arima_model.append(forecast).values[-500:]
actual = data.Users.values[-400:]
plt.figure(figsize=(15, 7))
plt.plot(forecast, color='r', label="model")
plt.title("SARIMA modeln Mean absolute error {} users".format(round(mean_absolute_error(data.dropna().Users, data.dropna().arima_model))))
plt.plot(actual, label="actual")
plt.legend()
plt.axvspan(len(actual), len(forecast), alpha=0.5, color='lightgrey')
plt.grid(True)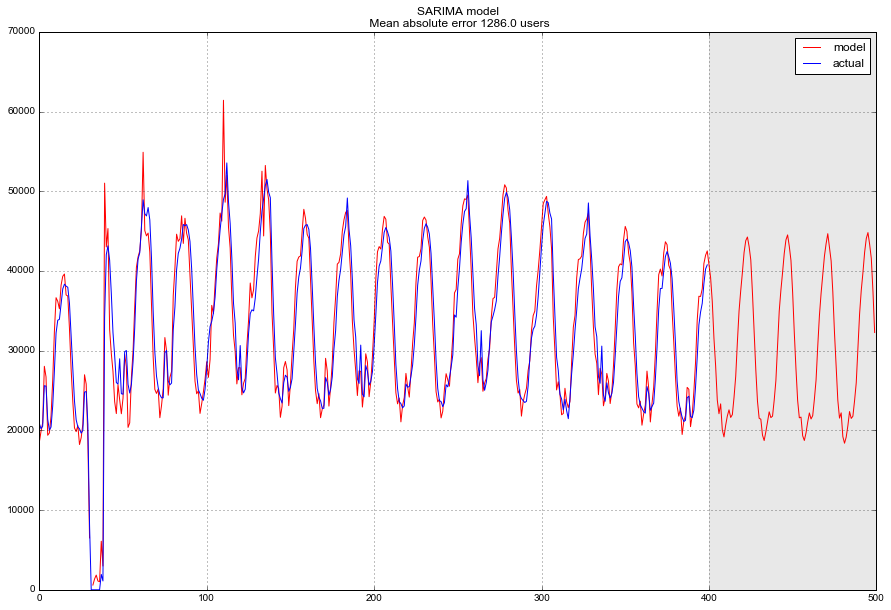
В финале получаем достаточно адекватный прогноз, в среднем модель ошибалась на 1.3 K пользователей, что очень и очень неплохо, однако суммарные затраты на подготовку данных, приведение к стационарности, определение и перебор параметров могут такой точности и не стоить.
Линейные и не очень модели на временных рядах
Снова небольшое лирическое отступление. Часто на работе приходится строить модели, руководствуясь одним основополагающим принципом – быстро, качественно, недорого. Поэтому часть моделей могут банально не подойти для “продакшн-решений”, так как либо требуют слишком больших затрат по подготовке данных (например, SARIMA), либо сложно настраиваются (хороший пример – SARIMA), либо требуют частого переобучения на новых данных (опять SARIMA), поэтому зачастую гораздо проще бывает выделить несколько признаков из имеющегося временного ряда и построить по ним обычную линейную регрессию или навесить решаюший лес. Дешево и сердито.
Возможно, этот подход не является значительно подкрепленным теорией, нарушает различные предпосылки, например, условия Гаусса-Маркова, особенно пункт про некоррелированность ошибок, однако на практике нередко выручает и достаточно активно используется в соревнованиях по машинному обучению.
Помимо стандартных признаков вроде лагов целевой переменной, много информации содержат в себе дата и время. Про извлечение признаков из них уже здорово описано в одной из предыдущих статей курса.
Добавлю только про еще один вариант кодирования категориальных признаков – кодирование средним. Если не хочется раздувать датасет множеством дамми-переменных, которые могут привести к потере информации о расстоянии, а в вещественном виде возникают противоречивые результаты а-ля “0 часов < 23 часа”, то можно закодировать переменную чуть более интерпретируемыми значениями. Естественный вариант – закодировать средним значением целевой переменной. В нашем случае каждый день недели или час дня можно закодировать сооветствующим средним числом игроков, находившихся в этот день недели или час онлайн. При этом важно следить за тем, чтобы расчет среднего значения производился только в рамках тестового датасета (или в рамках текущего наблюдаемого фолда при кросс-валидации), иначе можно ненароком привнести в модель информацию о будущем.
def code_mean(data, cat_feature, real_feature):
"""
Возвращает словарь, где ключами являются уникальные категории признака cat_feature,
а значениями - средние по real_feature
"""
return dict(data.groupby(cat_feature)[real_feature].mean())Создадим новый датафрейм и добавим в него час, день недели и выходной в качестве категориальных переменных. Для этого переводим имеющийся в датафрейме индекс в формат datetime, и извлекаем из него hour и weekday.
data = pd.DataFrame(dataset)
data.columns = ["y"]
data.index = data.index.to_datetime()
data["hour"] = data.index.hour
data["weekday"] = data.index.weekday
data['is_weekend'] = data.weekday.isin([5,6])*1
data.head()Out:Посмотрим на средние по дням недели
code_mean(data, 'weekday', "y")Out:
{0: 38730.143229166664,
1: 38632.828125,
2: 38128.518229166664,
3: 39519.035135135135,
4: 41505.152777777781,
5: 43717.708333333336,
6: 43392.143603133161}Помимо перечисленных преобразований для увеличения числа признаков используют и множество других метрик, например, максимальное/минимальное значение, наблюдавшееся в скользящем по ряду окне, медианы, число пиков, взвешенные дисперсии и многое другое. Автоматически этим занимается уже упоминавшаяся в курсе библиотека библиотека tsfresh.
Для удобства все преобразования можно записать в одну функцию, которая сразу же будет возвращать разбитые на трейн и тест датасеты и целевые переменные.
Функция для создания переменных
def prepareData(data, lag_start=5, lag_end=20, test_size=0.15):
data = pd.DataFrame(data.copy())
data.columns = ["y"]
# считаем индекс в датафрейме, после которого начинается тестовыый отрезок
test_index = int(len(data)*(1-test_size))
# добавляем лаги исходного ряда в качестве признаков
for i in range(lag_start, lag_end):
data["lag_{}".format(i)] = data.y.shift(i)
data.index = data.index.to_datetime()
data["hour"] = data.index.hour
data["weekday"] = data.index.weekday
data['is_weekend'] = data.weekday.isin([5,6])*1
# считаем средние только по тренировочной части, чтобы избежать лика
data['weekday_average'] = map(code_mean(data[:test_index], 'weekday', "y").get, data.weekday)
data["hour_average"] = map(code_mean(data[:test_index], 'hour', "y").get, data.hour)
# выкидываем закодированные средними признаки
data.drop(["hour", "weekday"], axis=1, inplace=True)
data = data.dropna()
data = data.reset_index(drop=True)
# разбиваем весь датасет на тренировочную и тестовую выборку
X_train = data.loc[:test_index].drop(["y"], axis=1)
y_train = data.loc[:test_index]["y"]
X_test = data.loc[test_index:].drop(["y"], axis=1)
y_test = data.loc[test_index:]["y"]
return X_train, X_test, y_train, y_testЛинейная регрессия vs XGBoost
Обучим на получившихся данных простую линейную регрессию. При этом лаги будем брать начиная с двенадцатого, таким образом модель будет способна строить предсказания на 12 часов вперёд, имея фактические наблюдения за предыдущие пол дня.
Построение линейной регрессии
from sklearn.linear_model import LinearRegression
X_train, X_test, y_train, y_test = prepareData(dataset.Users, test_size=0.3, lag_start=12, lag_end=48)
lr = LinearRegression()
lr.fit(X_train, y_train)
prediction = lr.predict(X_test)
plt.figure(figsize=(15, 7))
plt.plot(prediction, "r", label="prediction")
plt.plot(y_test.values, label="actual")
plt.legend(loc="best")
plt.title("Linear regressionn Mean absolute error {} users".format(round(mean_absolute_error(prediction, y_test))))
plt.grid(True);
Получилось достаточно неплохо, даже отбора признаков модель ошибается, в среднем, на 3K пользователей в час, и это учитывая огромный выброс в середине тестового ряда.
Также можно провести оценку модели на кросс-валидации, тому же принципу, что был использован ранее. Для этого воспользуемся функцией (с небольшими модификациями), предложенной в посте Pythonic Cross Validation on Time Series
Код для кросс-валидации
def performTimeSeriesCV(X_train, y_train, number_folds, model, metrics):
print('Size train set: {}'.format(X_train.shape))
k = int(np.floor(float(X_train.shape[0]) / number_folds))
print('Size of each fold: {}'.format(k))
errors = np.zeros(number_folds-1)
# loop from the first 2 folds to the total number of folds
for i in range(2, number_folds + 1):
print('')
split = float(i-1)/i
print('Splitting the first ' + str(i) + ' chunks at ' + str(i-1) + '/' + str(i) )
X = X_train[:(k*i)]
y = y_train[:(k*i)]
print('Size of train + test: {}'.format(X.shape)) # the size of the dataframe is going to be k*i
index = int(np.floor(X.shape[0] * split))
# folds used to train the model
X_trainFolds = X[:index]
y_trainFolds = y[:index]
# fold used to test the model
X_testFold = X[(index + 1):]
y_testFold = y[(index + 1):]
model.fit(X_trainFolds, y_trainFolds)
errors[i-2] = metrics(model.predict(X_testFold), y_testFold)
# the function returns the mean of the errors on the n-1 folds
return errors.mean()%%time
performTimeSeriesCV(X_train, y_train, 5, lr, mean_absolute_error)Size train set: (1838, 39)
Size of each fold: 367
Splitting the first 2 chunks at 1/2
Size of train + test: (734, 39)
Splitting the first 3 chunks at 2/3
Size of train + test: (1101, 39)
Splitting the first 4 chunks at 3/4
Size of train + test: (1468, 39)
Splitting the first 5 chunks at 4/5
Size of train + test: (1835, 39)
CPU times: user 59.5 ms, sys: 7.02 ms, total: 66.5 ms
Wall time: 18.9 ms
Out: 4613.17893150896
На 5 фолдах получили среднюю абсолютную ошибку в 4.6 K пользователей, достаточно близко к оценке качества, полученной на тестовом датасете.
Почему бы теперь не попробовать XGBoost…

Код для построения прогноза с XGBoost
import xgboost as xgb
def XGB_forecast(data, lag_start=5, lag_end=20, test_size=0.15, scale=1.96):
# исходные данные
X_train, X_test, y_train, y_test = prepareData(dataset.Users, lag_start, lag_end, test_size)
dtrain = xgb.DMatrix(X_train, label=y_train)
dtest = xgb.DMatrix(X_test)
# задаём параметры
params = {
'objective': 'reg:linear',
'booster':'gblinear'
}
trees = 1000
# прогоняем на кросс-валидации с метрикой rmse
cv = xgb.cv(params, dtrain, metrics = ('rmse'), verbose_eval=False, nfold=10, show_stdv=False, num_boost_round=trees)
# обучаем xgboost с оптимальным числом деревьев, подобранным на кросс-валидации
bst = xgb.train(params, dtrain, num_boost_round=cv['test-rmse-mean'].argmin())
# можно построить кривые валидации
#cv.plot(y=['test-mae-mean', 'train-mae-mean'])
# запоминаем ошибку на кросс-валидации
deviation = cv.loc[cv['test-rmse-mean'].argmin()]["test-rmse-mean"]
# посмотрим, как модель вела себя на тренировочном отрезке ряда
prediction_train = bst.predict(dtrain)
plt.figure(figsize=(15, 5))
plt.plot(prediction_train)
plt.plot(y_train)
plt.axis('tight')
plt.grid(True)
# и на тестовом
prediction_test = bst.predict(dtest)
lower = prediction_test-scale*deviation
upper = prediction_test+scale*deviation
Anomalies = np.array([np.NaN]*len(y_test))
Anomalies[y_test<lower] = y_test[y_test<lower]
plt.figure(figsize=(15, 5))
plt.plot(prediction_test, label="prediction")
plt.plot(lower, "r--", label="upper bond / lower bond")
plt.plot(upper, "r--")
plt.plot(list(y_test), label="y_test")
plt.plot(Anomalies, "ro", markersize=10)
plt.legend(loc="best")
plt.axis('tight')
plt.title("XGBoost Mean absolute error {} users".format(round(mean_absolute_error(prediction_test, y_test))))
plt.grid(True)
plt.legend()XGB_forecast(dataset, test_size=0.2, lag_start=5, lag_end=30)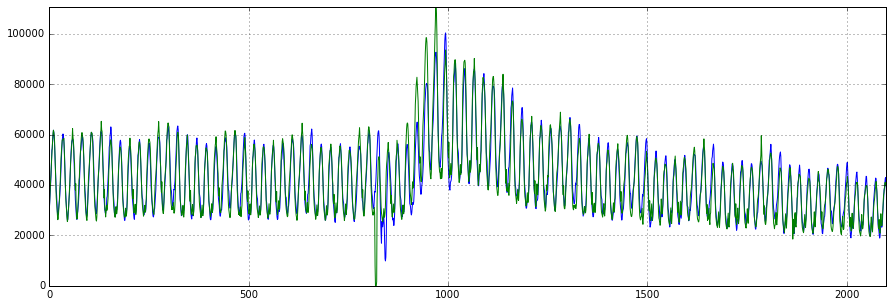

Те же 3 K пользователей в средней абсолютной ошибке, и неплохо пойманные аномалии на тестовом датасете. Конечно, чтобы уменьшить ошибку, еще можно повозиться с параметрами, настроить при необходимости регуляризацию, отобрать признаки, понять, на сколько лагов нужно уходить вглубь истории и т.д.
Заключение
Мы познакомились с разными методами и подходами к анализу и прогнозированию временных рядов. К сожалению, или к счастью, серебряной пули для решения такого рода задач пока не появилось. Методы, разработанные в 60-е годы прошлого века, (а некоторые и в начале 19-го), по-прежнему пользуются популярностью наравне с неразобранными в рамках данной статьи LSTM или RNN. Отчасти это связано с тем, что задача прогнозирования, как и любая другая задача, возникающая в процессе работы с данными — во многом творческая и уж точно исследовательская. Несмотря на обилие формальных метрик качества и способов оценки параметров, для каждого временного ряда часто приходится подбирать и пробовать что-то своё. Не последнюю роль играет и баланс между качеством и трудозатратами. Не раз уже упоминавшаяся здесь SARIMA-модель хотя и демонстрирует выдающиеся результаты при должной настройке, может потребовать не одного часа танцев с бубном манипуляций с рядом, в то время как простенькую линейную регрессию можно соорудить за 10 минут, получив при этом более-менее сравнимые результаты.
Домашнее задание №9
В демо-версии домашнего задания вы будете предсказывать просмотры wiki-страницы “Machine Learning”. Веб-форма для ответов, там же найдете и решение.
Актуальные и обновляемые версии демо-заданий – на английском на сайте курса, вот первое задание. Также по подписке на Patreon (“Bonus Assignments” tier) доступны расширенные домашние задания по каждой теме (только на англ.).
Полезные ресурсы
- Open Machine Learning Course. Topic 9. Part 1. Time series analysis in Python
- Видеозапись лекции по мотивам этой статьи
- Open Machine Learning Course. Topic 9. Part 2. Predicting the future with Facebook Prophet
- Онлайн-учебник курса по продвинутому статистическому прогнозированию университета Duke — разобраны всевозможные сглаживания, линейные модели и ARIMA модели
- Статья Comparison of ARIMA and Random Forest time series models for prediction of avian influenza H5N1 outbreaks — одна из немногих, где активно защищается позиция случайного леса в задачах по прогнозированию временных рядов
- Статья Time Series Analysis (TSA) in Python — Linear Models to GARCH семействе моделей ARIMA и их применении для моделирования финансовых показателей (Brian Christopher)
Материал статьи доступен в GitHub-репозитории курса
в виде тетрадок Jupyter.
Введение
В настоящее время известно большое количество различных методов прогнозирования, основывающихся только на анализе прошлых значений временной последовательности, то есть методов, использующих принципы, принятые в техническом анализе. Основным инструментом этих методов является схема экстраполяции, когда свойства последовательности, выявленные на рассматриваемом интервале времени распространяются за его пределы.
При этом предполагается, что свойства последовательности в будущем будут такими же, как в прошлом и настоящем. Реже в процессе прогнозирования используется более сложная схема экстраполяции, предполагающая исследование динамики изменения свойств последовательности и учет этой динамики на интервале прогноза.
Наверное, наиболее известными методами прогнозирования, основанными на экстраполяции, являются методы, использующие модель авторегрессии и скользящего среднего (ARIMA). Своей популярностью эти методы, в первую очередь, обязаны работам Бокса и Дженкинса (Boks Dzh., Dzhenkins G.), предложившим и развившим обобщенную модель ARIMA. Но кроме представленных Боксом и Дженкинсом
моделей, конечно, существуют и другие модели и методы прогнозирования.
В данной статье будут кратко рассмотрены более простые модели – модели экспоненциального сглаживания, которые были предложены Хольтом (Holt C.C) и Брауном (Brown R.G) еще до появления работ Бокса и Дженкинса.
Несмотря на более простой и доступный математический аппарат, прогнозирование при помощи моделей экспоненциального сглаживания часто дает результат, сопоставимый с результатом, полученным при использовании модели ARIMA. Это неудивительно, так как модели экспоненциального сглаживания являются частным случаем моделей ARIMA. Другими словами, каждая рассматриваемая в статье модель экспоненциального сглаживания имеет соответствующую эквивалентную модель ARIMA. Эти эквивалентные модели в статье рассматриваться не будут и приведены лишь для информации.
Известно, что процесс прогнозирования в каждом конкретном случае требует индивидуального подхода и обычно включает в себя целый ряд процедур.
Например:
- Анализ временной последовательности на предмет наличия пропущенных и выпадающих значений. Коррекция этих значений.
- Определение наличия тренда и его типа. Определение наличия периодичности в последовательности.
- Проверка последовательности на стационарность.
- Анализ последовательности на предмет необходимости предварительной обработки (логарифмирование, взятие разностей и так далее).
- Выбор модели.
- Определение параметров модели. Прогноз на основании выбранной модели.
- Оценка точности прогнозирования модели.
- Анализ характера ошибок выбранной модели.
- Определение адекватности выбранной модели и в случае необходимости ее замена и возвращение к предыдущим пунктам.
Здесь приведен далеко не полный список действий, необходимых для получения эффективного прогноза.
Следует подчеркнуть тот факт, что определение параметров модели и непосредственно получение прогноза являются лишь небольшой частью общей процедуры прогнозирования. Но рассмотреть в статье весь круг вопросов, так или иначе связанных с прогнозированием, не представляется возможным.
Поэтому в данной статье ограничимся только рассмотрением непосредственно самих моделей экспоненциального сглаживания, а в качестве тестовых последовательностей будем использовать котировки валют, без какой-либо их предварительной обработки. Конечно, совсем избежать в статье сопутствующих вопросов не удастся, но они будут затронуты лишь в объеме, необходимом для рассмотрения самих моделей.
1. Стационарность
Само понятие экстраполяции предполагает, что рассматриваемый процесс в будущем будет развиваться так же, как в прошлом и настоящем. Другими словами, речь идет о стационарности процесса. Стационарный процесс является наиболее привлекательным с точки зрения построения прогнозов, но, к сожалению, в природе таких процессов не существует, любой реальный процесс по мере своего развития подвержен изменениям.
У реальных процессов с течением времени могут заметно меняться математическое ожидание, дисперсия, закон распределения, но процессы, у которых эти характеристики изменяются очень медленно можно с той или иной вероятностью отнести к стационарным процессам. В данном случае понятие “очень медленно” означает, что изменение характеристик процесса на конечном интервале наблюдения оказывается настолько незначительным, что этими изменениями можно пренебречь.
Понятно, что чем короче доступный интервал наблюдения (короткая выборка), тем выше вероятность принятия ошибочного решения о стационарности процесса в целом. С другой стороны, если нас в большей степени интересует состояние процесса в более поздние моменты времени, и мы собираемся производить прогноз на очень короткий интервал, сокращение размера выборки в некоторых случаях может привести к увеличению точности такого прогноза.
Если процесс подвержен изменениям, то параметры последовательности, определенные на интервале наблюдения, за его пределами будут изменяться. Таким образом, чем длиннее интервал прогноза, тем большее влияние на погрешность прогноза будет оказывать изменчивость характеристик последовательности. Этот факт заставляет ограничиться лишь краткосрочным прогнозом, сильное сокращение интервала прогноза позволяет ожидать, что медленно изменяющиеся характеристики последовательности не внесут в прогноз существенных погрешностей.
Кроме того, изменчивость параметров последовательности приводит к тому, что при оценке по интервалу наблюдения мы получаем некоторое усредненное их значение, так как на этом интервале они не оставались постоянными. Поэтому найденные значения параметров не будут относиться к последнему моменту времени этого интервала, а будут отражать некоторое среднее их значение. Полностью устранить это неприятное явление, к сожалению, не представляется возможным, но его можно ослабить, если по возможности сокращать длительность интервала наблюдения, на котором производится оценка параметров модели (интервал обучения).
Укорачивать до бесконечности этот интервал тоже нельзя, так как при чрезмерном сокращении интервала обучения наверняка будет снижаться точность оценки параметров последовательности. Необходимо искать компромисс между влиянием ошибок, связанных с изменчивостью характеристик последовательности и возрастанием погрешностей, связанных с чрезмерным сокращением интервала обучения.
Все сказанное в полной мере относится к прогнозированию с использованием моделей экспоненциального сглаживания, так как эти модели построены исходя из предположения стационарности процессов, как впрочем, и модели ARIMA. Тем не менее, для упрощения в дальнейшем будем условно предполагать, что у всех рассматриваемых нами последовательностей их параметры на интервале наблюдения изменяются, но происходит это настолько медленно, что этими изменениями можно пренебречь.
Таким образом, в статье будут рассматриваться вопросы, связанные с краткосрочным прогнозированием последовательностей с медленно меняющимися характеристиками на базе моделей экспоненциального сглаживания. В данном случае понятие “краткосрочное прогнозирование” следует понимать как прогнозирование на один, два или несколько интервалов времени вперед, а не в смысле прогнозирования на период менее одного года, как это зачастую принято в экономике.
2. Тестовые последовательности
При написании статьи использовались предварительно сохраненные для периодов M1, M5, M30 и H1 котировки EURRUR, EURUSD, USDJPY и XAUUSD. Каждый из сохраненных файлов содержит по 1100 значений “open”. Самое “старое” значение расположено в начале файла, а самое “новое” в конце. Самое последнее значение, записанное в файл, соответствует времени создания файла. Файлы с тестовыми последовательностями были созданы при помощи скрипта HistoryToCSV.mq5. Сами файлы с данными и скрипт, при помощи которого они были созданы, размещены в конце статьи в архиве Files.zip.
Как уже упоминалось, сохраненные котировки в данной статье используются без какой-либо предварительной обработки, несмотря на явные проблемы, на которые все же хочется обратить внимание. Например, котировки EURRUR_H1 в течение суток содержат то 12, то 13 бар, котировки XAUUSD по пятницам содержат на один бар меньше, чем в другие дни. Эти примеры показывают, что котировки представлены с неравномерным шагом дискретизации, и это совершенно неприемлемо для алгоритмов, рассчитанных на работу с корректными временными последовательностями, предполагающими равномерный шаг квантования.
Даже если при помощи интерполяции восстановить недостающие значения котировок, то открытым остается вопрос об отсутствии котировок в выходные дни. Можно предположить, что события, происходящие в мире в выходные дни, влияют на состояние мировой экономики не меньше, чем события, происходящие по будням. Революции, природные явления, громкие скандалы, смена правительства и другие более или менее крупные события подобного рода могут произойти когда угодно. Если такое событие произошло в субботу, то вряд ли оно окажет меньшее влияние на мировые рынки, чем в случае, если бы оно произошло в рабочий день.
Возможно, именно такие события приводят к тому, что мы часто наблюдаем разрывы котировок на границе рабочей недели. Скорее всего, мир продолжает существовать по своим законам даже тогда, когда FOREX не работает. Пока совершенно неясно, нужно ли в котировках, предназначенных для технического анализа восстанавливать значения, соответствующие выходным дням, даст ли это какую-либо выгоду?
Эти вопросы явно выходят за рамки данной статьи, но на первый взгляд, последовательность, не имеющая пропусков, представляется для анализа более привлекательной, хотя бы с точки зрения обнаружения циклических (сезонных) составляющих.
Значение предварительной подготовки данных для последующего анализа трудно переоценить, в данном случае это отдельная большая тема, так как котировки, в том виде, как они представлены в терминале, вообще малопригодны для технического анализа. К уже упомянутым проблемам с пропуском данных можно добавить еще целый ряд.
Например, при формировании котировок фиксированному моменту времени присваиваются значения “open” и “close” ему не принадлежащие, эти значения соответствуют времени формирования тика, а не фиксированному моменту выбранного таймфрейма графика, при этом тики, как известно иногда поступают очень редко.
Другой пример, это полное игнорирование теоремы Котельникова, ведь никто не дает гарантии, что хотя бы на минутном интервале частота дискретизации удовлетворяет упомянутой теореме (не говоря уже о других, более старших интервалах). Кроме всего прочего необходимо помнить и о наличии переменного спреда, который в некоторых случаях может наложиться на значения котировок.
Все же оставим все эти вопросы за рамками данной статьи и вернемся к ее непосредственной теме.
3. Экспоненциальное сглаживание
Для начала рассмотрим самую простую модель
![]() ,
,
где:
- X(t) – исследуемый (моделируемый) процесс,
- L(t) – изменяющийся уровень процесса,
- r(t)– случайная величина с нулевым средним значением.
Как видим, модель включает в себя сумму двух компонент, из которых нас интересует уровень процесса L(t), именно его мы и попытаемся выделить.
Хорошо известно, что при усреднении случайной последовательности можно добиться снижения ее дисперсии, то есть уменьшить размах ее отклонения от среднего значения. Поэтому можно предположить, что если процесс, описываемый нашей простейшей моделью подвергнуть усреднению (сглаживанию), то мы сможем если не совсем избавиться от случайной компоненты r(t), то хотя бы заметно ее ослабить, выделив тем самым интересующий нас уровень L(t).
Для этого обратимся к простому экспоненциальному сглаживанию (Simple Exponential Smoothing, SES).
![]()
В этом хорошо известном выражении степень сглаживания задается коэффициентом альфа, который можно установить в интервале от 0 до 1. При выборе значения альфа, равным нулю, вновь поступающие величины входной последовательности X не смогут оказать никакого влияния на результат сглаживания. Результатом сглаживания для любых моментов времени будет являться постоянная величина.
Таким образом, в этом крайнем случае мы полностью подавим мешающую случайную компоненту, но при этом и интересующий нас уровень процесса будет сглажен до состояния горизонтальной прямой линии. Если значение коэффициента альфа установить равным единице, то на входную последовательность процесс сглаживания вообще не будет оказывать никакого влияния. При этом интересующий нас уровень L(t) не будет искажен, но и случайная компонента подавлена не будет.
Интуитивно понятно, что при выборе величины альфа необходимо одновременно удовлетворять противоречивым требованиям. С одной стороны значение альфа должно быть близко к нулю, чтобы эффективно подавить случайную составляющую r(t). С другой, чтобы не исказить интересующую нас компоненту L(t), желательно выбирать значение альфа, близким к единице. Для нахождения оптимального значения альфа нам необходимо определить критерий, по которому это значение можно будет оптимизировать.
При определении такого критерия вспомним, что в данной статье речь идет о прогнозировании, а не просто о сглаживании последовательности.
В данном случае для простой модели экспоненциального сглаживания прогнозом на любое количество шагов вперед принято считать найденное в данный момент времени значение ![]() .
.
![]()
где ![]() – прогноз в момент времени t на m шагов вперед.
– прогноз в момент времени t на m шагов вперед.
Значит, прогнозом значения последовательности на момент времени t будет являться прогноз, сделанный на предыдущем шаге на один шаг вперед
![]()
В этом случае в качестве критерия для оптимизации значения коэффициента альфа можно использовать ошибку предсказания на один шаг
![]()
Таким образом, если минимизировать сумму квадратов этих ошибок по всей выборке, то можно будет определить оптимальное значение коэффициента альфа для данной последовательности. Естественно, наилучшим значением альфа будет такое, при котором величина суммы квадратов ошибок окажется минимальной.
На рисунке 1 приведен график зависимости суммы квадратов ошибок прогноза на один шаг вперед от величины коэффициента альфа для фрагмента тестовой последовательности USDJPY M1.
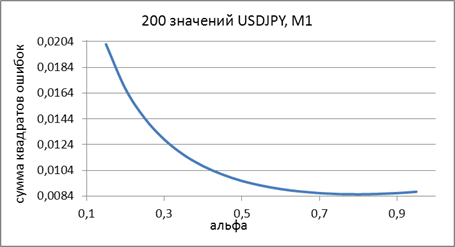
Рисунок 1. Простое экспоненциальное сглаживание
На полученном графике слабо различим минимум, примерно в районе значения альфа, равном 0,8. Но такую картину для простого экспоненциального сглаживания можно наблюдать далеко не всегда. При попытке определить оптимальное значение альфа для фрагментов тестовых последовательностей, используемых в статье, мы чаще всего будем получать непрерывно спадающий к единице график.
Столь высокие оптимальные значения коэффициента сглаживания говорят о том, что такая простейшая модель плохо подходит для описания наших тестовых последовательностей (котировок). Или уровень процесса L(t) изменяется слишком быстро, или в процессе присутствует тренд.
Несколько усложним нашу модель, добавив в нее ещё одну компоненту
![]() ,
,
где:
- X(t) – исследуемый (моделируемый) процесс;
- L(t) – изменяющийся уровень процесса;
- T(t) – линейный тренд;
- r(t) – случайная величина с нулевым средним значением.
Известно, что коэффициенты линейной регрессии можно определить, осуществив двойное сглаживание последовательности:
![]()
![]()
![]()
![]()
Для найденных таким образом коэффициентов a1 и a2 прогноз в момент времени t на m шагов вперед будет равен
![]()
Следует обратить внимание на тот факт, что в приведенных выражениях при первом и повторном сглаживании используется одинаковый коэффициент альфа. Такую модель называют аддитивной однопараметрической моделью линейного роста.
Продемонстрируем различие между простой моделью и моделью линейного роста.
Предположим, что на протяжении длительного времени исследуемый процесс представлял собой постоянную составляющую, то есть на графике выглядел как прямая горизонтальная линия и в какой-то момент времени начался линейный тренд. Прогноз такого процесса, сделанный упомянутыми моделями, показан на рисунке 2.
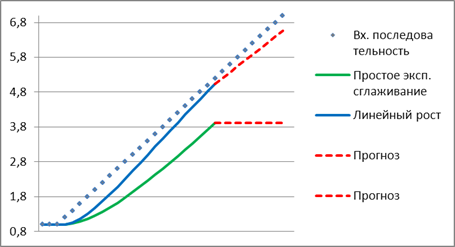
Рисунок 2. Сравнение моделей
Как видим, модель простого экспоненциального сглаживания заметно отстает от линейно изменяющейся входной последовательности, а прогноз, сделанный при помощи этой модели, еще больше от нее удаляется. При использовании модели линейного роста наблюдается иная картина. При возникновении тренда эта модель стремиться, как бы догнать линейно изменяющуюся последовательность, а ее прогноз лучше совпадает с направлением изменения входных значений.
Если бы в приведенном примере был выбран коэффициент сглаживания большей величины, то модель линейного роста за указанный промежуток времени вполне успела бы “догнать” входной сигнал, а ее прогноз практически совпал бы с входной последовательностью.
Несмотря на то, что в установившемся состоянии модель линейного роста при наличии линейного тренда показывает хороший результат, нетрудно заметить, что ей требуется определенное время для того чтобы “догнать” тренд. Поэтому, при частой смене направления тренда между моделью и входной последовательностью все время будет наблюдаться расхождение. Кроме того, если тренд нарастает не линейно, а по квадратичному закону, то модель линейного роста уже будет не в состоянии его “догнать”. Но, несмотря на эти недостатки, при линейном тренде модель имеет преимущества перед моделью простого экспоненциального сглаживания.
Как уже упоминалось, мы использовали однопараметрическую модель линейного роста. Для поиска оптимального значения параметра альфа для фрагмента тестовой последовательности USDJPY M1 построим график зависимости суммы квадратов ошибок прогноза на один шаг вперед от величины этого параметра.
График такой зависимости показан на рисунке 3, при построении графика был использован тот же фрагмент последовательности, что и при построении графика, показанного на рисунке 1.
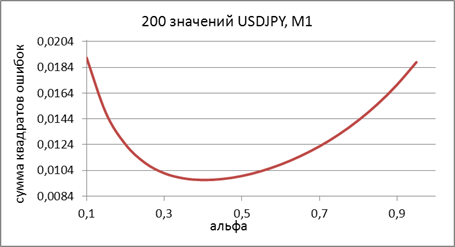
Рисунок 3. Модель линейного роста
По сравнению с результатом, показанным на рисунке 1, в данном случае величина оптимального значения для коэффициента альфа снизилась до значения, примерно равного 0,4. В данной модели для первого и второго сглаживания выбираются одинаковые коэффициенты, хотя теоретически они могут иметь разную величину. Модель линейного роста с двумя различными коэффициентами сглаживания будет представлена далее.
Обе рассмотренные модели экспоненциального сглаживания имеют свои аналоги в виде индикаторов, поставляемых в составе MetaTrader 5. Это хорошо известные EMA и DEMA, но предназначены они не для получения прогноза, а для сглаживания значений последовательности.
Следует учитывать, что при использовании индикатора DEMA на экран выводится значение соответствующее коэффициенту a1, а не значение прогноза на один шаг вперед. Коэффициент a2 (см. приведенные выше выражения для модели линейного роста) при этом не вычисляется и не используется. Кроме того, значение коэффициента сглаживания вычисляется через величину эквивалентного периода n
![]()
Для примера, значению альфа равному 0,8 будет соответствовать величина n примерно равная 2, а при значении альфа равным 0,4 величина n равна 4.
4. Начальные значения
Как уже упоминалось, при применении экспоненциального сглаживания необходимо тем или иным способом выбрать величину коэффициента сглаживания. Но этого оказывается недостаточно. Так как при экспоненциальном сглаживании текущее значение вычисляется на основе предыдущего, то для нулевого момента времени возникает ситуация, когда такое значение еще отсутствует. То есть, для нулевого момента времени, каким-то образом должны быть определенны начальное значение для S или для S1 и S2 в случае модели линейного роста.
Проблема выбора начальных значений не всегда легко разрешима. Если (как в случае использования котировок в MetaTrader 5) нам доступна очень длительная история, то даже при неточном определении начальных значений кривая экспоненциального сглаживания к текущему моменту времени успеет стабилизироваться, скорректировав нашу начальную ошибку. На это может понадобиться примерно от 10 до 200 (а иногда и больше) периодов в зависимости от величины коэффициента сглаживания.
В этой ситуации достаточно грубо оценить исходные значения и начать процесс экспоненциального сглаживания заранее, за 200-300 периодов до интересующего нас участка времени. Сложнее дело обстоит, когда в нашем распоряжении имеется выборка, содержащая, например, всего 100 значений.
В литературе можно встретить разные рекомендации по выбору начальных значений. Например, начальное значение для простого экспоненциального сглаживания может быть приравнено первому элементу последовательности или в надежде на сглаживание случайных выбросов может быть найдено как среднее значение трех-четырех начальных элементов последовательности. Для модели линейного роста начальные значения S1 и S2 могут быть определены исходя из предположения, что начальный уровень прогнозной кривой должен быть равен первому элементу последовательности, а наклон линейного тренда равен нулю.
В различных источниках можно найти еще целый ряд рекомендаций по выбору начальных значений, но все они не могут обеспечить отсутствие весьма чувствительных ошибок на начальных шагах алгоритма сглаживания. Особенно это заметно при использовании коэффициентов сглаживания с низкими значениями, когда для достижения стабильного состояния требуется большое количество периодов.
Поэтому чтобы свести к минимуму влияние проблем, связанных с выбором начальных значений (особенно для коротких последовательностей) иногда используют метод, предполагающий поиск таких значений, при которых ошибка прогноза окажется минимальной. Речь идет о вычислении ошибки прогноза по всей последовательности для изменяющихся с небольшим шагом величин исходных значений.
Наиболее удачный вариант можно выбрать после вычисления величины ошибки по сетке всех возможных комбинаций исходных значений. Но такой способ является очень трудоемким, требует большого количества вычислений и в прямом виде практически не используется.
Описанная задача является задачей оптимизации или поиска минимального значения функции многих переменных. Для решения подобного рода задач разработаны различные алгоритмы, позволяющие существенно сократить требуемые объемы вычислений. К вопросам оптимизации параметров сглаживания и начальных значений при прогнозировании вернемся несколько позже.
5. Оценка точности прогноза
В процессе прогнозирования и выбора начальных значений или параметров модели возникает задача оценки точности прогнозирования. Оценка точности важна и при сравнении между собой различных моделей или при определении состоятельности полученного прогноза. Известно большое количество оценок, определяющих точность прогнозирования, но для вычисления любой из них необходимо знать на каждом шаге ошибку прогнозирования.
Как уже упоминалось, ошибка прогнозирования на один шаг вперед в момент времени t равна
![]()
где:
 – значение входной последовательности в момент времени t;
– значение входной последовательности в момент времени t; – прогноз на момент времени t сделанный на предыдущем шаге.
– прогноз на момент времени t сделанный на предыдущем шаге.
Наверное, наиболее распространенной оценкой точности прогнозирования является среднее значение квадратов ошибок (Mean Squared Error):
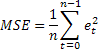
где n – количество элементов последовательности.
Иногда, в качестве недостатка оценки MSE указывают на ее чрезмерную чувствительность к редким одиночным ошибкам большой величины. Это объясняется тем, что значение ошибки при вычислении MSE возводится в квадрат. В этом случае в качестве альтернативы предлагается использовать среднее значение абсолютной ошибки (Mean Absolute Error)
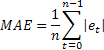
Здесь операция возведения значения ошибки в квадрат заменена на использование абсолютного ее значения. Предполагается, что при использовании MAE можно получить более устойчивые оценки.
Обе эти оценки хорошо подходят, например, для определения точности прогноза одной и той же последовательности при различных параметрах модели или при использовании различных моделей, но они оказываются малопригодными для сравнения между собой результатов прогнозирования, полученных на разных последовательностях.
Кроме того, непосредственно по величине этих оценок нельзя определить, насколько хорош результат прогнозирования. Например, получив значение MAE равное 0,03, или какое либо другое, мы не можем сказать хорошо это или плохо.
Для того чтобы иметь возможность сравнивать между собой точность
прогноза разных последовательностей можно использовать относительные оценки RelMSE и RelMAE:
![]()
При этом найденные оценки точности прогноза делятся на
соответствующие оценки, полученные при использовании тестового метода
прогнозирования. В качестве такого тестового метода удобно использовать так
называемый наивный метод, когда предполагается, что значение процесса в будущем
будет равно его значению в данный момент времени.
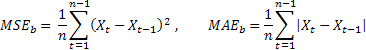
Если средняя величина ошибок прогнозирования равна
величине ошибок полученных при использовании наивного метода, то значение
относительных оценок будет равно единице. Если значение относительных оценок
меньше единицы, то это означает, что в среднем величина ошибок прогноза меньше,
чем при наивном методе. То есть, точность результатов прогноза превосходит
точность наивного метода. И наоборот, если значение относительных оценок больше
единицы, то точность результатов прогноза в среднем хуже, чем при наивном
методе прогнозирования.
Эти оценки так же пригодны для определения точности прогноза на два или более шагов вперед. Для этого нужно лишь вместо ошибки прогноза на один шаг при их расчете использовать значение ошибок прогноза на соответствующее количество шагов вперед.
Для примера в таблице приведены ошибки прогноза на один
шаг вперед RelMAE при использовании однопараметрической модели линейного
роста. Подсчет ошибок производился по 200 последним значениям каждой тестовой последовательности.
|
Таблица 1. Ошибки прогноза RelMAE на один шаг вперед.
Оценка RelMAE позволяет сравнить между собой эффективность
выбранного метода при прогнозировании разных последовательностей. Как видно из
результатов, приведенных в таблице 1, нам ни разу не удалось произвести прогноз
точнее, чем в случае использования наивного метода, все значения RelMAE больше единицы.
6. Аддитивные модели
Ранее в статье уже приводилась модель, которая включала в себя сумму уровня процесса, линейного тренда и случайной величины. В список рассматриваемых в статье моделей добавим еще и модель, которая в дополнение к перечисленным компонентам в виде суммы включает в себя циклическую, сезонную составляющую.
Модели экспоненциального сглаживания, в которых все компоненты входят в виде суммы, называют аддитивными моделями. Кроме таких моделей существуют мультипликативные модели, в которых одна, несколько или все компоненты входят в них в виде произведения. Перейдем к рассмотрению группы аддитивных моделей.
В прошлых разделах уже не раз упоминалось об ошибке прогноза, сделанного на один шаг вперед. Практически в любых приложениях, связанных с прогнозированием, на основе экспоненциального сглаживания приходится вычислять значение этой ошибки. Зная величину ошибки прогнозирования, выражения для представленных ранее моделей экспоненциального сглаживания можно записать в несколько иной форме (форма с коррекцией ошибки).
В данном случае будем использовать форму представления модели, когда в ее выражениях ошибка частично или полностью суммируется с ранее полученными значениями. Такое представление называют моделями с аддитивной ошибкой. Модели экспоненциального сглаживания также могут быть выражены и в форме с мультипликативной ошибкой, но в
данной статье такое представление моделей использовать не будем.
Рассмотрим аддитивные модели экспоненциального
сглаживания.
Простое экспоненциальное сглаживание:
![]()
![]()
Эквивалентная модель – ARIMA(0,1,1): ![]()
Аддитивная модель линейного роста:
![]()
![]()
![]()
В отличие от ранее представленной однопараметрической модели линейного роста, в данном случае используются два различных параметра сглаживания.
Эквивалентная модель – ARIMA(0,2,2): ![]()
Модель линейного роста с демпфированием:
![]()
![]()
![]()
Смысл такого демпфирования заключается в том, что на каждом последующем шаге прогнозирования крутизна тренда будет убывать в зависимости от величины значения коэффициента демпфирования. Этот эффект демонстрируется на рисунке 4.
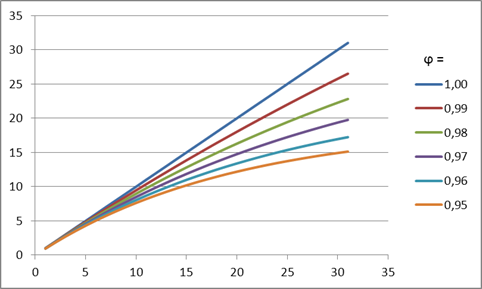
Рисунок 4. Влияние коэффициента демпфирования
Как следует из приведенного рисунка, при построении прогноза, с уменьшением величины коэффициента демпфирования тренд все быстрее будет терять свою силу, таким образом, линейный рост оказывается все более демпфированным.
Эквивалентная модель – ARIMA(1,1,2): ![]()
К каждой из этих трех моделей можно в виде суммы добавить сезонную составляющую, при этом получим еще три модели.
Простая модель с аддитивной сезонностью:
![]()
![]()
![]()
Модель линейного роста с аддитивной сезонностью:
![]()
![]()
![]()
![]()
Модель линейного роста с демпфированием и аддитивной сезонностью:
![]()
![]()
![]()
![]()
Для моделей с сезонностью также существуют эквивалентные модели ARIMA, но они здесь не приводятся, так как вряд ли будут иметь какое-либо практическое значение.
В приведенных выражениях используются следующие обозначения:
Нетрудно заметить, что выражения для последней из приведенных моделей включают в себя все шесть рассматриваемых вариантов.
Если в
выражениях для модели линейного роста с демпфированием и аддитивной сезонностью
принять
![]() ,
,
то при вычислении прогноза сезонность учитываться не будет. Далее, при ![]() будет получена модель линейного роста, а при
будет получена модель линейного роста, а при ![]() получим модель линейного роста с демпфированием.
получим модель линейного роста с демпфированием.
Значениям ![]() будет соответствовать модель простого экспоненциального сглаживания.
будет соответствовать модель простого экспоненциального сглаживания.
При применении моделей, учитывающих сезонность, вначале необходимо каким-либо доступным методом определить наличие цикличности и период цикла, затем эти данные использовать для инициализации значения сезонных индексов.
В нашем случае, когда прогноз производится на коротких интервалах времени, обнаружить значительную устойчивую цикличность в используемых фрагментах тестовых последовательностей не удалось. Поэтому в статье не будем приводить примеры и подробно рассматривать особенности, связанные с учетом сезонности.
Для определения вероятностных пределов прогноза (prediction intervals) для рассматриваемых моделей воспользуемся аналитическим выводами, представленными в литературе [3]. В качестве оценки дисперсии ошибок прогноза на один шаг вперед будем использовать среднее значение суммы их квадратов, вычисленное по всей выборке размером n.
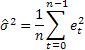
Тогда для определения величины дисперсии при прогнозе на 2 и более шагов вперед для рассматриваемых моделей будет справедливо выражение:
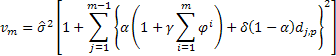
где ![]() равняется единице в случае, если j, взятое по модулю p равно нулю, в противном случае
равняется единице в случае, если j, взятое по модулю p равно нулю, в противном случае ![]() равно нулю.
равно нулю.
Вычислив значение дисперсии прогноза для каждого шага m, можно найти границы прогноза для 95% вероятностного интервала:
![]()
Далее такой вероятностный диапазон условимся называть доверительным интервалом прогноза.
Используя приведенные для моделей экспоненциального сглаживания выражения, реализуем их в виде класса написанного на MQL5.
7. Программная реализация класса AdditiveES
При реализации в виде класса использовались выражения для модели линейного роста с демпфированием и аддитивной сезонностью.
Как упоминалось ранее, остальные модели могут быть получены из нее путем соответствующего выбора параметров.
#property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> class AdditiveES:public CObject { protected: double Alpha; double Gamma; double Phi; double Delta; int nSes; double S; double T; double Ises[]; int p_Ises; double F; public: AdditiveES(); double Init(double s,double t,double alpha=1,double gamma=0, double phi=1,double delta=0,int nses=1); double GetS() { return(S); } double GetT() { return(T); } double GetF() { return(F); } double GetIs(int m); void IniIs(int m,double is); double NewY(double y); double Fcast(int m); double VarCoefficient(int m); }; void AdditiveES::AdditiveES() { Alpha=0.5; Gamma=0; Delta=0; Phi=1; nSes=1; ArrayResize(Ises,nSes); ArrayInitialize(Ises,0); p_Ises=0; S=0; T=0; } double AdditiveES::Init(double s,double t,double alpha=1,double gamma=0, double phi=1,double delta=0,int nses=1) { S=s; T=t; Alpha=alpha; if(Alpha<0)Alpha=0; if(Alpha>1)Alpha=1; Gamma=gamma; if(Gamma<0)Gamma=0; if(Gamma>1)Gamma=1; Phi=phi; if(Phi<0)Phi=0; if(Phi>1)Phi=1; Delta=delta; if(Delta<0)Delta=0; if(Delta>1)Delta=1; nSes=nses; if(nSes<1)nSes=1; ArrayResize(Ises,nSes); ArrayInitialize(Ises,0); p_Ises=0; F=S+Phi*T; return(F); } double AdditiveES::NewY(double y) { double e; e=y-F; S=S+Phi*T+Alpha*e; T=Phi*T+Alpha*Gamma*e; Ises[p_Ises]=Ises[p_Ises]+Delta*(1-Alpha)*e; p_Ises++; if(p_Ises>=nSes)p_Ises=0; F=S+Phi*T+GetIs(0); return(F); } double AdditiveES::GetIs(int m) { if(m<0)m=0; int i=(int)MathMod(m+p_Ises,nSes); return(Ises[i]); } void AdditiveES::IniIs(int m,double is) { if(m<0)m=0; if(m<nSes) { int i=(int)MathMod(m+p_Ises,nSes); Ises[i]=is; } } double AdditiveES::Fcast(int m) { int i,h; double v,v1; if(m<1)h=1; else h=m; v1=1; v=0; for(i=0;i<h;i++){v1=v1*Phi; v+=v1;} return(S+v*T+GetIs(h)); } double AdditiveES::VarCoefficient(int m) { int i,h; double v,v1,a,sum,k; if(m<1)h=1; else h=m; if(h==1)return(1); v=0; v1=1; sum=0; for(i=1;i<h;i++) { v1=v1*Phi; v+=v1; if((int)MathMod(i,nSes)==0)k=1; else k=0; a=Alpha*(1+v*Gamma)+k*Delta*(1-Alpha); sum+=a*a; } return(1+sum); }
Кратко рассмотрим методы класса AdditiveES.
Метод Init
Входные параметры:
- double s – устанавливаемое начальное значение сглаженного уровня;
- double t – устанавливаемое начальное значение сглаженного тренда;
- double alpha=1 – устанавливаемый параметр сглаживания уровня последовательности;
- double gamma=0 – устанавливаемый параметр сглаживания тренда;
- double phi=1 – устанавливаемый параметр демпфирования;
- double delta=0 – устанавливаемый параметр сглаживания сезонных индексов;
- int nses=1 – устанавливаемое количество периодов в сезонном цикле.
Возвращаемое значение:
- Возвращает вычисленный на основании установленных начальных значений прогноз на один шаг вперед.
Обращение к методу Init необходимо производить в самую первую очередь. Это необходимо для установки параметров сглаживания и начальных значений. Следует отметить, что метод Init не предусматривает возможности инициализации сезонных индексов произвольными значениями, сезонные индексы при обращении к нему всегда будут установлены в нуль.
Метод IniIs
Входные параметры:
- Int m – номер сезонного индекса;
- double is – устанавливаемое значение сезонного индекса с номером m.
Возвращаемое значение:
- Нет
Обращение к методу IniIs(…) производится в случае необходимости присвоить сезонным индексам начальные значения отличные от нуля. Производить инициализацию сезонных индексов следует сразу после обращения к методу Init(…).
Метод NewY
Входные параметры:
- double y – новое значение входной последовательности
Возвращаемое значение:
- Возвращает вычисленный на основании нового поступившего значения последовательности прогноз на один шаг вперед
Метод, предназначенный для вычисления прогноза на один шаг вперед при поступлении каждого следующего значения входной последовательности. Обращаться к методу следует только после инициализации класса методами Init и при необходимости IniIs.
Метод Fcast
Входные параметры:
- int m – горизонт прогнозирования 1,2,3,… периода;
Возвращаемое значение:
- Возвращает значение прогноза, сделанного на m-шагов вперед.
Метод только рассчитывает значение прогноза, не влияя на состояние процесса сглаживания. Обычно обращение к нему должно производиться после обращения к методу NewY.
Метод VarCoefficient
Входные параметры:
- int m – горизонт прогнозирования 1,2,3,… периода;
Возвращаемое значение:
- Возвращает значение коэффициента для вычисления дисперсии прогноза.
Вычисляется значение коэффициента показывающего насколько возрастет величина дисперсии для прогноза на m-шагов по сравнению с дисперсией прогноза на один шаг вперед.
Методы GetS, GetT, GetF, GetIs
Методы служат для обеспечения доступа к защищенным переменным класса. GetS, GetT и GetF возвращают значения сглаженного уровня, сглаженного значения тренда и значение прогноза на один шаг соответственно. Метод GetIs обеспечивает доступ к сезонным индексам и требует в качестве входного аргумента указания номера индекса m.
Самой сложной из рассматриваемых нами моделей является модель линейного
роста с демпфированием и аддитивной сезонностью , на основе которой и создан класс AdditiveES. Совершенно резонно возникает вопрос, для чего тогда могут понадобиться остальные более простые модели?
Несмотря на то, что на первый взгляд более сложные модели должны иметь явное преимущество перед более простыми, на самом деле это далеко не всегда так. Более простые модели, имеющие меньшее число параметров в подавляющем большинстве случаев будут обеспечивать меньшую величину дисперсии ошибок прогнозирования, то есть будут работать более устойчиво. Этот факт используют при создании алгоритмов прогнозирования базирующихся на одновременной параллельной работе всех имеющихся в наличии моделей, от самых простых до самых сложных.
После того как последовательность полностью обработана, для прогнозирования выбирается модель, показавшая наименьшее значение ошибки с учетом числа ее параметров (то есть с учетом ее сложности). Для такого выбора разработан ряд критериев, например Akaike’s Information Criterion (AIC). В результате будет выбрана модель, от которой ожидается получение наиболее устойчивого прогноза.
Для демонстрации использования класса AdditiveES был создан несложный индикатор, в котором все параметры сглаживания задаются вручную.
Исходный код индикатора AdditiveES_Test.mq5 приводится ниже.
#property copyright "2011, victorg" #property link "https://www.mql5.com" #property indicator_chart_window #property indicator_buffers 4 #property indicator_plots 4 #property indicator_label1 "History" #property indicator_type1 DRAW_LINE #property indicator_color1 clrDodgerBlue #property indicator_style1 STYLE_SOLID #property indicator_width1 1 #property indicator_label2 "Forecast" #property indicator_type2 DRAW_LINE #property indicator_color2 clrDarkOrange #property indicator_style2 STYLE_SOLID #property indicator_width2 1 #property indicator_label3 "PInterval+" #property indicator_type3 DRAW_LINE #property indicator_color3 clrCadetBlue #property indicator_style3 STYLE_SOLID #property indicator_width3 1 #property indicator_label4 "PInterval-" #property indicator_type4 DRAW_LINE #property indicator_color4 clrCadetBlue #property indicator_style4 STYLE_SOLID #property indicator_width4 1 double HIST[]; double FORE[]; double PINT1[]; double PINT2[]; input double Alpha=0.2; input double Gamma=0.2; input double Phi=0.8; input double Delta=0; input int nSes=1; input int nHist=250; input int nTest=150; input int nFore=12; #include "AdditiveES.mqh" AdditiveES fc; int NHist; int NFore; int NTest; double ALPH; double GAMM; double PHI; double DELT; int nSES; int OnInit() { NHist=nHist; if(NHist<100)NHist=100; NFore=nFore; if(NFore<2)NFore=2; NTest=nTest; if(NTest>NHist)NTest=NHist; if(NTest<50)NTest=50; ALPH=Alpha; if(ALPH<0)ALPH=0; if(ALPH>1)ALPH=1; GAMM=Gamma; if(GAMM<0)GAMM=0; if(GAMM>1)GAMM=1; PHI=Phi; if(PHI<0)PHI=0; if(PHI>1)PHI=1; DELT=Delta; if(DELT<0)DELT=0; if(DELT>1)DELT=1; nSES=nSes; if(nSES<1)nSES=1; MqlRates rates[]; CopyRates(NULL,0,0,NHist,rates); SetIndexBuffer(0,HIST,INDICATOR_DATA); PlotIndexSetString(0,PLOT_LABEL,"History"); SetIndexBuffer(1,FORE,INDICATOR_DATA); PlotIndexSetString(1,PLOT_LABEL,"Forecast"); PlotIndexSetInteger(1,PLOT_SHIFT,NFore); SetIndexBuffer(2,PINT1,INDICATOR_DATA); PlotIndexSetString(2,PLOT_LABEL,"Conf+"); PlotIndexSetInteger(2,PLOT_SHIFT,NFore); SetIndexBuffer(3,PINT2,INDICATOR_DATA); PlotIndexSetString(3,PLOT_LABEL,"Conf-"); PlotIndexSetInteger(3,PLOT_SHIFT,NFore); IndicatorSetInteger(INDICATOR_DIGITS,_Digits); return(0); } int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,j,init,start; double v1,v2; if(rates_total<NHist){Print("Error: Not enough bars for calculation!"); return(0);} if(prev_calculated>rates_total||prev_calculated<=0||(rates_total-prev_calculated)>1) {init=1; start=rates_total-NHist;} else {init=0; start=prev_calculated;} if(start==rates_total)return(rates_total); if(init==1) { i=start; v2=(open[i+2]-open[i])/2; v1=(open[i]+open[i+1]+open[i+2])/3.0-v2; fc.Init(v1,v2,ALPH,GAMM,PHI,DELT,nSES); ArrayInitialize(HIST,EMPTY_VALUE); } PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFore); PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFore); PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFore); for(i=start;i<rates_total;i++) { HIST[i]=fc.NewY(open[i]); } v1=0; for(i=0;i<NTest;i++) { j=rates_total-NTest+i; v2=close[j]-HIST[j-1]; v1+=v2*v2; } v1/=NTest; j=1; for(i=rates_total-NFore;i<rates_total;i++) { v2=1.96*MathSqrt(v1*fc.VarCoefficient(j)); FORE[i]=fc.Fcast(j++); PINT1[i]=FORE[i]+v2; PINT2[i]=FORE[i]-v2; } return(rates_total); }
При запуске или повторной инициализации индикатора происходит установка начальных значений экспоненциального сглаживания
![]()
Для сезонных индексов в данном индикаторе начальных
установок не производится, поэтому их начальные значения всегда оказываются
равны нулю. При такой инициализации влияние сезонности на результат прогноза
при поступлении новых значений будет постепенно возрастать от нуля, до какой-то
установившейся величины.
Количество циклов, необходимых для достижения
установившегося режима, зависит от величины коэффициента сглаживания сезонных
индексов: чем ниже значение коэффициента сглаживания, тем больше времени на это
потребуется.
На рисунке 5 показан результат работы индикатора AdditiveES_Test.mq5 с установками по умолчанию.
Рисунок 5. Индикатор AdditiveES_Test.mq5
Кроме непосредственно прогноза индикатор дополнительно выводит линию, соответствующую прогнозу на один шаг для прошлых значений последовательности и границы 95% доверительного интервала прогноза.
Доверительный интервал строится на основе оценки дисперсии ошибки на один шаг вперед. Для того чтобы снизить влияние неточностей, допущенных при выборе начальных значений, эта оценка производится не по всей длине nHist, а только по последним барам, количество которых указывается во входном параметре nTest.
В конце статьи размещен архив Files.zip, включающий в себя файлы AdditiveES.mqh и AdditiveES_Test.mq5. При компиляции индикатора необходимо, чтобы включаемый файл AdditiveES.mqh был расположен в том же каталоге, что и AdditiveES_Test.mq5.
Если при построении индикатора AdditiveES_Test.mq5 проблема выбора начальных значений хоть как-то была решена, то проблема с выбором оптимальных значений параметров сглаживания так и осталась открытой.
8. Выбор оптимальных значений параметров
Простая модель экспоненциального сглаживания имеет единственный параметр сглаживания и для поиска его оптимального значения можно воспользоваться методом простого перебора. Произведя по всей последовательности расчет величины ошибок прогнозирования, изменим на небольшой шаг значение параметра и вновь произведем полный расчет. Будем повторять эту процедуру до тех пор, пока не переберем все возможные значения параметра. Далее
нам останется только выбрать значение параметра, при котором была получена
наименьшая величина ошибок.
Для того чтобы искать оптимальное значение коэффициента сглаживания в диапазоне от 0.1 до 0.9 с шагом 0.05, нам понадобиться семнадцать раз произвести полный расчет величины ошибок прогнозирования. Как видим, требуется не так уж много вычислений. Но для модели линейного роста с демпфированием оптимизировать необходимо уже три параметра сглаживания, и для того чтобы перебрать все их комбинации по сетке с тем же шагом 0.05, потребуется уже 4913 проходов.
Количество полных проходов, которое требуется для перебора всех возможных значений параметров, очень быстро возрастает с увеличением количества параметров, уменьшением шага их изменения и увеличением диапазона поиска. Если в дальнейшем возникнет необходимость кроме параметров сглаживания оптимизировать и начальные значения моделей, то методом простого перебора это сделать уже будет достаточно сложно.
Проблемы, связанные с поиском минимума функций многих переменных хорошо изучены и существует достаточно много различных алгоритмов такого рода. Описание и сравнение разных методов поиска минимума функции можно найти в литературе [7]. Все эти методы в первую очередь направлены на уменьшение количества обращений к целевой функции, то есть на снижение вычислительных затрат в процессе поиска минимума.
Часто в различной литературе можно встретить упоминание о так называемых квазиньютоновских методах оптимизации. Скорее всего, это связано с высокой их эффективностью, но для демонстрации подхода к оптимизации процесса прогнозирования достаточно будет реализовать какой-нибудь более простой метод. Остановим свой выбор на методе Пауэлла. Метод Пауэлла не требует вычисления производных целевой функции и относится к методам поиска.
Программно данный метод, впрочем, как и любой другой, может быть реализован по-разному. Окончание поиска может осуществляться при достижении определенной точности по значению целевой функции или по значению аргумента. Кроме того, конкретная реализация может включать в себя возможность использования ограничений на допустимый диапазон изменения параметров функции.
В нашем случае алгоритм безусловного поиска минимума методом Пауэлла реализован в виде класса PowellsMethod. Алгоритм прекращает поиск при достижении заданной точности по значению целевой функции. В качестве прототипа при реализации данного метода был использован алгоритм, приведенный в литературе [8].
Ниже приведен исходный код класса PowellsMethod.
#property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #define GOLD 1.618034 #define CGOLD 0.3819660 #define GLIMIT 100.0 #define SHFT(a,b,c,d) (a)=(b);(b)=(c);(c)=(d); #define SIGN(a,b) ((b) >= 0.0 ? fabs(a) : -fabs(a)) #define FMAX(a,b) (a>b?a:b) class PowellsMethod:public CObject { protected: double P[],Xi[]; double Pcom[],Xicom[],Xt[]; double Pt[],Ptt[],Xit[]; int N; double Fret; int Iter; int ItMaxPowell; double FtolPowell; int ItMaxBrent; double FtolBrent; int MaxIterFlag; public: void PowellsMethod(void); void SetItMaxPowell(int n) { ItMaxPowell=n; } void SetFtolPowell(double er) { FtolPowell=er; } void SetItMaxBrent(int n) { ItMaxBrent=n; } void SetFtolBrent(double er) { FtolBrent=er; } int Optimize(double &p[],int n=0); double GetFret(void) { return(Fret); } int GetIter(void) { return(Iter); } private: void powell(void); void linmin(void); void mnbrak(double &ax,double &bx,double &cx,double &fa,double &fb,double &fc); double brent(double ax,double bx,double cx,double &xmin); double f1dim(double x); virtual double func(const double &p[]) { return(0); } }; void PowellsMethod::PowellsMethod(void) { ItMaxPowell= 200; FtolPowell = 1e-6; ItMaxBrent = 200; FtolBrent = 1e-4; } void PowellsMethod::powell(void) { int i,j,m,n,ibig; double del,fp,fptt,t; n=N; Fret=func(P); for(j=0;j<n;j++)Pt[j]=P[j]; for(Iter=1;;Iter++) { fp=Fret; ibig=0; del=0.0; for(i=0;i<n;i++) { for(j=0;j<n;j++)Xit[j]=Xi[j+n*i]; fptt=Fret; linmin(); if(fabs(fptt-Fret)>del){del=fabs(fptt-Fret); ibig=i;} } if(2.0*fabs(fp-Fret)<=FtolPowell*(fabs(fp)+fabs(Fret)+1e-25))return; if(Iter>=ItMaxPowell) { Print("powell exceeding maximum iterations!"); MaxIterFlag=1; return; } for(j=0;j<n;j++){Ptt[j]=2.0*P[j]-Pt[j]; Xit[j]=P[j]-Pt[j]; Pt[j]=P[j];} fptt=func(Ptt); if(fptt<fp) { t=2.0*(fp-2.0*(Fret)+fptt)*(fp-Fret-del)*(fp-Fret-del)-del*(fp-fptt)*(fp-fptt); if(t<0.0) { linmin(); for(j=0;j<n;j++){m=j+n*(n-1); Xi[j+n*ibig]=Xi[m]; Xi[m]=Xit[j];} } } } } void PowellsMethod::linmin(void) { int j,n; double xx,xmin,fx,fb,fa,bx,ax; n=N; for(j=0;j<n;j++){Pcom[j]=P[j]; Xicom[j]=Xit[j];} ax=0.0; xx=1.0; mnbrak(ax,xx,bx,fa,fx,fb); Fret=brent(ax,xx,bx,xmin); for(j=0;j<n;j++){Xit[j]*=xmin; P[j]+=Xit[j];} } void PowellsMethod::mnbrak(double &ax,double &bx,double &cx, double &fa,double &fb,double &fc) { double ulim,u,r,q,fu,dum; fa=f1dim(ax); fb=f1dim(bx); if(fb>fa) { SHFT(dum,ax,bx,dum) SHFT(dum,fb,fa,dum) } cx=bx+GOLD*(bx-ax); fc=f1dim(cx); while(fb>fc) { r=(bx-ax)*(fb-fc); q=(bx-cx)*(fb-fa); u=bx-((bx-cx)*q-(bx-ax)*r)/(2.0*SIGN(FMAX(fabs(q-r),1e-20),q-r)); ulim=bx+GLIMIT*(cx-bx); if((bx-u)*(u-cx)>0.0) { fu=f1dim(u); if(fu<fc){ax=bx; bx=u; fa=fb; fb=fu; return;} else if(fu>fb){cx=u; fc=fu; return;} u=cx+GOLD*(cx-bx); fu=f1dim(u); } else if((cx-u)*(u-ulim)>0.0) { fu=f1dim(u); if(fu<fc) { SHFT(bx,cx,u,cx+GOLD*(cx-bx)) SHFT(fb,fc,fu,f1dim(u)) } } else if((u-ulim)*(ulim-cx)>=0.0){u=ulim; fu=f1dim(u);} else {u=cx+GOLD*(cx-bx); fu=f1dim(u);} SHFT(ax,bx,cx,u) SHFT(fa,fb,fc,fu) } } double PowellsMethod::brent(double ax,double bx,double cx,double &xmin) { int iter; double a,b,d,e,etemp,fu,fv,fw,fx,p,q,r,tol1,tol2,u,v,w,x,xm; a=(ax<cx?ax:cx); b=(ax>cx?ax:cx); d=0.0; e=0.0; x=w=v=bx; fw=fv=fx=f1dim(x); for(iter=1;iter<=ItMaxBrent;iter++) { xm=0.5*(a+b); tol2=2.0*(tol1=FtolBrent*fabs(x)+2e-19); if(fabs(x-xm)<=(tol2-0.5*(b-a))){xmin=x; return(fx);} if(fabs(e)>tol1) { r=(x-w)*(fx-fv); q=(x-v)*(fx-fw); p=(x-v)*q-(x-w)*r; q=2.0*(q-r); if(q>0.0)p=-p; q=fabs(q); etemp=e; e=d; if(fabs(p)>=fabs(0.5*q*etemp)||p<=q*(a-x)||p>=q*(b-x)) d=CGOLD*(e=(x>=xm?a-x:b-x)); else {d=p/q; u=x+d; if(u-a<tol2||b-u<tol2)d=SIGN(tol1,xm-x);} } else d=CGOLD*(e=(x>=xm?a-x:b-x)); u=(fabs(d)>=tol1?x+d:x+SIGN(tol1,d)); fu=f1dim(u); if(fu<=fx) { if(u>=x)a=x; else b=x; SHFT(v,w,x,u) SHFT(fv,fw,fx,fu) } else { if(u<x)a=u; else b=u; if(fu<=fw||w==x){v=w; w=u; fv=fw; fw=fu;} else if(fu<=fv||v==x||v==w){v=u; fv=fu;} } } Print("Too many iterations in brent"); MaxIterFlag=1; xmin=x; return(fx); } double PowellsMethod::f1dim(double x) { int j; double f; for(j=0;j<N;j++) Xt[j]=Pcom[j]+x*Xicom[j]; f=func(Xt); return(f); } int PowellsMethod::Optimize(double &p[],int n=0) { int i,j,k,ret; k=ArraySize(p); if(n==0)N=k; else N=n; if(N<1||N>k)return(0); ArrayResize(P,N); ArrayResize(Xi,N*N); ArrayResize(Pcom,N); ArrayResize(Xicom,N); ArrayResize(Xt,N); ArrayResize(Pt,N); ArrayResize(Ptt,N); ArrayResize(Xit,N); for(i=0;i<N;i++)for(j=0;j<N;j++)Xi[i+N*j]=(i==j?1.0:0.0); for(i=0;i<N;i++)P[i]=p[i]; MaxIterFlag=0; powell(); for(i=0;i<N;i++)p[i]=P[i]; if(MaxIterFlag==1)ret=-1; else ret=Iter; return(ret); }
Основным методом класса является метод Optimize.
Метод Optimize
Входные параметры :
- double &p[] – массив, содержащий на входе начальные величины параметров, оптимальное значение которых должно быть найдено, на выходе массив содержит найденные оптимальные значения этих параметров.
- int n=0 – количество аргументов в массиве p[]. При n=0 количество параметров считается равным размеру массива p[].
Возвращаемое значение:
- Возвращает количество итераций, которое потребовалось для работы алгоритма, или -1 если было достигнуто максимально
допустимое их количество.
В процессе поиска оптимальных значений параметров происходит итеративное приближение к точке минимума целевой функции. Метод Optimize возвращает количество итераций, понадобившихся для достижения минимума функции с заданной точностью. На каждой итерации происходит несколько обращений к целевой функции, то есть количество вызовов целевой функции может значительно (в десятки, а то и в сотни раз) превышать количество итераций, возвращаемое методом Optimize.
Другие методы класса.
Метод SetItMaxPowell
Входные параметры:
- Int n – максимально допустимое для метода Пауэлла количество итераций. Значение по умолчанию 200.
Возвращаемое значение:
- Нет.
Задается максимально допустимое количество итераций, при достижении которого поиск будет прекращен независимо от того, удалось или нет обнаружить с заданной точностью минимум целевой функции. При этом в журнал будет выведено соответствующее сообщение.
Метод SetFtolPowell
Входные параметры:
- double er – точность. Величина отклонения от значения минимума целевой функции, при достижении которой метод Пауэлла прекращает поиск. Значение по умолчанию 1e-6.
Возвращаемое значение:
- Нет.
Метод SetItMaxBrent
Входные параметры:
- Int n – максимально допустимое количество итераций для вспомогательного метода Брента. Значение по умолчанию 200.
Возвращаемое значение:
- Нет.
Задается максимально допустимое количество итераций. При его достижении вспомогательный метод Брента прекратит поиск и в журнал будет выведено соответствующее сообщение.
Метод SetFtolBrent
Входные параметры:
- double er – точность. Величина, определяющая точность при поиске минимума для вспомогательного метода Брента. Значение по умолчанию 1e-4.
Возвращаемое значение:
- Нет.
Метод GetFret
Входные параметры:
- Нет.
Возвращаемое значение:
- Возвращает найденное минимальное значение целевой функции.
Метод GetIter
Входные параметры:
- Нет.
Возвращаемое значение:
- Возвращает количество итераций, которое потребовалось для работы алгоритма.
Виртуальная функция func(const double &p[])
Входные параметры:
- const double &p[] – адрес массива содержащего
оптимизируемые параметры. Размер массива соответствует количеству параметров функции.
Возвращаемое значение:
- Возвращает значение функции
соответствующее переданным ей параметрам.
Виртуальначя
функция func() в каждом конкретном случае должна быть переопределена в
производном от PowellsMethod классе. Функция func()
является целевой функцией, для которой при обращении к алгоритму поиска будут
найдены ее аргументы, соответствующие минимальному возвращаемому функцией
значению.
В данной реализации метода Пауэлла для определения направления поиска по каждому из параметров используется одномерный метод параболической интерполяции Брента. Точность и максимально допустимое количество итераций для этих методов можно задавать раздельно при помощи обращения к SetItMaxPowell, SetFtolPowell, SetItMaxBrent и SetFtolBrent.
Таким образом можно изменить принятые по умолчанию характеристики алгоритма. Это может понадобиться в случае, если, например, для конкретной целевой функции, установленная по умолчанию точность оказалась завышенной и в процессе поиска алгоритму требуется слишком большое количество итераций. Изменением значения требуемой точности можно оптимизировать процедуру поиска для различных категорий целевых функций.
Несмотря на кажущуюся сложность алгоритма, реализующего метод Пауэлла, использовать его достаточно просто.
Приведем пример. Пусть у нас имеется функция
![]()
и нам необходимо найти величины параметров ![]() и
и ![]() , при которых функция будет иметь наименьшее значение.
, при которых функция будет иметь наименьшее значение.
Создадим скрипт, демонстрирующий способ решения этой задачи.
#property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" class PM_Test:public PowellsMethod { public: void PM_Test(void) {} private: virtual double func(const double &p[]); }; double PM_Test::func(const double &p[]) { double f,r1,r2; r1=p[0]-0.5; r2=p[1]-6.0; f=r1*r1*4.0+r2*r2; return(f); } void OnStart() { int it; double p[2]; p[0]=8; p[1]=9; PM_Test *pm = new PM_Test; it=pm.Optimize(p); Print("Iter= ",it," Fret= ",pm.GetFret()); Print("p[0]= ",p[0]," p[1]= ",p[1]); delete pm; }
При написании скрипта в первую очередь была создана
как член класса PM_Test
функция func(), которая по переданным ей величинам параметров p[0] и p[1] вычисляет значение заданной тестовой функции. Далее в теле функции OnStart() искомым параметрам присваиваются начальные значения. С этих значений будет начат поиск.
Далее
создается экземпляр класса PM_Test и обращением к методу Optimize производится
запуск процесса поиска искомых величин p[0] и p[1], при этом методы родительского
класса PowellsMethod будут обращаться к переопределенной нами функции func(). По завершении поиска в журнал будет выведено количество произведенных итераций, значение функции в точке найденного минимума и найденные значения параметров p[0]=0.5 и p[1]=6.
Файл PowellsMethod.mqh и тестовый пример PM_Test.mq5 размещены в конце статьи в архиве Files.zip. Для того чтобы откомпилировать PM_Test.mq5, необходимо, чтобы он был расположен в том же каталоге, что и файл PowellsMethod.mqh.
9. Оптимизация значений параметров модели
В предыдущем разделе была представлена реализация метода поиска минимума функции и приведен простой пример ее использования. Теперь перейдем к рассмотрению вопросов, связанных с оптимизацией параметров непосредственно самой модели экспоненциального сглаживания.
Для начала максимально упростим представленный ранее класс AdditiveES, исключив из него все элементы, связанные с учетом сезонной компоненты, так как далее в статье все равно не предполагается рассматривать модели, учитывающие сезонность. Это позволит исходный код класса сделать более легким для восприятия и сократить количество вычислений. Кроме того, так же исключим все вычисления связанные с прогнозированием и расчетом доверительных интервалов прогноза, так легче продемонстрировать подход к оптимизации параметров используемой модели линейного роста с демпфированием.
#property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" class OptimizeES:public PowellsMethod { protected: double Dat[]; int Dlen; double Par[5]; int NCalc; public: void OptimizeES(void) {} int Calc(string fname); private: int readCSV(string fnam,double &dat[]); virtual double func(const double &p[]); }; int OptimizeES::Calc(string fname) { int i,it; double relmae,naiv,s,t,alp,gam,phi,e,ae,pt; if(readCSV(fname,Dat)<0){Print("Error."); return(-1);} Dlen=ArraySize(Dat); NCalc=200; if(NCalc<0||NCalc>Dlen-1){Print("Error."); return(-1);} Par[0]=Dat[Dlen-NCalc]; Par[1]=0; Par[2]=0.5; Par[3]=0.5; Par[4]=0.5; it=Optimize(Par); s=Par[0]; t=Par[1]; alp=Par[2]; gam=Par[3]; phi=Par[4]; relmae=0; naiv=0; for(i=Dlen-NCalc;i<Dlen;i++) { e=Dat[i]-(s+phi*t); relmae+=MathAbs(e); naiv+=MathAbs(Dat[i]-Dat[i-1]); ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } relmae/=naiv; PrintFormat("%s: N=%i, RelMAE=%.3f",fname,NCalc,relmae); PrintFormat("Iter= %i, Fmin= %e",it,GetFret()); PrintFormat("p[0]= %.5f, p[1]= %.5f, p[2]= %.2f, p[3]= %.2f, p[4]= %.2f", Par[0],Par[1],Par[2],Par[3],Par[4]); return(0); } int OptimizeES::readCSV(string fnam,double &dat[]) { int n,asize,fhand; fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI); if(fhand==INVALID_HANDLE) { Print("FileOpen Error!"); return(-1); } asize=512; ArrayResize(dat,asize); n=0; while(FileIsEnding(fhand)!=true) { dat[n++]=FileReadNumber(fhand); if(n+128>asize) { asize+=128; ArrayResize(dat,asize); } } FileClose(fhand); ArrayResize(dat,n-1); return(0); } double OptimizeES::func(const double &p[]) { int i; double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt; s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1; if (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;} else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;} if (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;} else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;} if (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; } else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;} sse=0; for(i=Dlen-NCalc;i<Dlen;i++) { e=Dat[i]-(s+phi*t); sse+=e*e; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } return(NCalc*MathLog(k1*k2*k3*sse)); }
Класс OptimizeES создан как производный от класса PowellsMethod и в него включено переопределение виртуальной функция func(). Как уже ранее упоминалось, на вход этой функции должны передаваться параметры, для которых вычисляется значение, величина которого будет минимизироваться в процессе оптимизации.
В соответствии с методом максимального правдоподобия в функции func() вычисляется логарифм суммы квадрата ошибок предсказания на один шаг вперед. Вычисление ошибок производится в цикле для NCalc последних значений последовательности.
Для сохранения устойчивости модели нам необходимо ввести ограничения на диапазон изменения ее параметров. Определим этот диапазон для параметров Alpha и Gamma от значения 0.05 до 0.95, а для параметра Phi от 0.05 до 1.0. Но в нашем случае для оптимизации используется метод безусловного поиска минимума, не предусматривающий использования ограничений на значения аргументов целевой функции.
Для того чтобы учесть налагаемые на параметры ограничения и при этом не изменять алгоритм поиска, попытаемся свести задачу поиска минимума функции многих переменных с ограничениями к задаче безусловного поиска минимума. Для этого воспользуемся так называемым методом штрафных функций. Этот метод легко продемонстрировать для одномерного случая.
Предположим, что у нас имеется функция одного аргумента (область определения которой лежит в диапазоне от 2.0 до 3.0) и алгоритм, который в процессе поиска может задавать любые значения параметру этой функции. В этом случае можно поступить следующим образом: если алгоритм поиска передал аргумент, превосходящий максимально допустимое значение, например 3.5, то можно вычислить функцию для аргумента равного 3.0, а затем полученный результат умножить на коэффициент, пропорциональный величине превышения максимального значения, например, k=1+(3.5-3)*200.
Если таким же образом поступить и со значениями аргумента, которые оказались ниже минимально возможного, то нам гарантировано возрастание результирующей целевой функции за пределами допустимого диапазона изменений ее аргумента. Такое искусственное увеличение возвращаемого значения целевой функции позволяет скрыть от алгоритма, осуществляющего поиск, тот факт, что передаваемый функции аргумент был каким-то образом ограничен, и гарантировать то, что минимум результирующей функции будет располагаться в заданных пределах аргумента. Такой подход легко переносится и на случай функции нескольких переменных.
Осовноым методом класса OptimizeES является метод Calc. При обращении к этому методу производится чтение данных из файла, поиск оптимальных величин параметров модели и для найденных значений параметров вычисляется оценка точности предсказания RelMAE. При этом количество обрабатываемых значений считанной из файла последовательности, задается в переменной NCalc.
Ниже приведен пример скрипта Optimization_Test.mq5, использующего класс OptimizeES.
#property copyright "2011, victorg" #property link "https://www.mql5.com" #include "OptimizeES.mqh" OptimizeES es; void OnStart() { es.Calc("Dataset\USDJPY_M1_1100.TXT"); }
В результате исполнения этого скрипта мы должны получить следующий результат.

Рисунок 6. Результат исполнения скрипта Optimization_Test.mq5
Несмотря на то, что мы получили возможность находить оптимальные значения параметров и начальных значений модели, все же остается один параметр, оптимизировать который простыми средствами не удастся – это количество значений последовательности, по которым производится оптимизация. Производя оптимизацию по последовательности большой длинны, мы будем получать оптимальные значения параметров, в среднем обеспечивающих минимальную ошибку на всей ее длине.
Но если характер последовательности на протяжении этого интервала изменялся, то для отдельных ее фрагментов найденные значения уже не будут являться оптимальными. С другой стороны, если резко сократить длину последовательности, то мы получим оптимальные параметры для этого короткого отрезка, но в этом случае нет никакой гарантии, что эти значения будут оптимальными и на более продолжительном интервале времени.
Файлы OptimizeES.mqh и Optimization_Test.mq5 размещены в конце статьи в архиве Files.zip. При компиляции необходимо, чтобы файлы OptimizeES.mqh и PowellsMethod.mqh были размещены в том же каталоге, что и компилируемый файл Optimization_Test.mq5. В приведенном примере используется содержащий тестовую последовательность файл USDJPY_M1_1100.TXT, который должен находиться в каталоге MQL5FilesDataset.
В таблице 2 приведены значения оценки точности прогнозирования RelMAE, полученные при помощи этого скрипта. Прогнозирование производилось для восьми тестовых последовательностей, о которых говорилось в начале статьи. При построении прогноза использовались 100, 200 и 400 последних значений каждой из этих последовательностей.
| N=100 | N=200 | N=400 | |
|---|---|---|---|
| EURRUR M1 |
0.980 | 1.000 | 0.968 |
| EURRUR M30 |
0.959 | 0.992 | 0.981 |
| EURUSD M1 |
0.995 | 0.981 | 0.981 |
| EURUSD M30 |
1.023 | 0.985 | 0.999 |
| USDJPY M1 |
1.004 | 0.976 | 0.989 |
| USDJPY M30 |
0.993 | 0.987 | 0.988 |
| XAUUSD M1 |
0.976 | 0.993 | 0.970 |
| XAUUSD M30 |
0.973 | 0.985 | 0.999 |
Таблица 2. Ошибки прогнозирования RelMAE.
Как видим, оценки величины ошибок прогноза оказались близкими к единице, но в большинстве случаев точность прогноза используемой модели для заданных последовательностей превышает точность наивного метода.
10. Индикатор IndicatorES.mq5
Ранее при рассмотрении класса AdditiveES.mqh был приведен индикатор AdditiveES_Test.mq5, построенный на базе этого класса. В этом индикаторе все параметры сглаживания задавались вручную.
Теперь после рассмотрения метода, позволяющего производить оптимизацию параметров модели, можно создать такой же индикатор, оптимальные значения параметров и начальных значений которого будут определяться автоматически, задавать вручную нужно будет только длину обрабатываемой выборки. При этом исключим вычисления связанные с учетом сезонности.
Ниже приведен исходный код класса CIndiсatorES который используется при написании индикатора.
#property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" class CIndicatorES:public PowellsMethod { protected: double Dat[]; int Dlen; double Par[5]; public: void CIndicatorES(void) { } void CalcPar(double &dat[]); double GetPar(int n) { if(n>=0||n<5)return(Par[n]); else return(0); } private: virtual double func(const double &p[]); }; void CIndicatorES::CalcPar(double &dat[]) { Dlen=ArraySize(dat); ArrayResize(Dat,Dlen); ArrayCopy(Dat,dat); Par[0]=Dat[0]; Par[1]=0; Par[2]=0.5; Par[3]=0.5; Par[4]=0.5; Optimize(Par); } double CIndicatorES::func(const double &p[]) { int i; double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt; s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1; if (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;} else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;} if (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;} else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;} if (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; } else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;} sse=0; for(i=0;i<Dlen;i++) { e=Dat[i]-(s+phi*t); sse+=e*e; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } return(Dlen*MathLog(k1*k2*k3*sse)); }
Данный класс содержит методы CalcPar и GetPar, первый из которых предназначен для вычисления оптимального значения параметров модели, а второй для доступа к этим значениям. Кроме того, класс CIndicatorES включает в себя переопределение виртуальной функции func().
Исходный код индикатора IndicatorES.mq5:
#property copyright "2011, victorg" #property link "https://www.mql5.com" #property indicator_chart_window #property indicator_buffers 4 #property indicator_plots 4 #property indicator_label1 "History" #property indicator_type1 DRAW_LINE #property indicator_color1 clrDodgerBlue #property indicator_style1 STYLE_SOLID #property indicator_width1 1 #property indicator_label2 "Forecast" #property indicator_type2 DRAW_LINE #property indicator_color2 clrDarkOrange #property indicator_style2 STYLE_SOLID #property indicator_width2 1 #property indicator_label3 "ConfUp" #property indicator_type3 DRAW_LINE #property indicator_color3 clrCrimson #property indicator_style3 STYLE_DOT #property indicator_width3 1 #property indicator_label4 "ConfDn" #property indicator_type4 DRAW_LINE #property indicator_color4 clrCrimson #property indicator_style4 STYLE_DOT #property indicator_width4 1 input int nHist=80; #include "CIndicatorES.mqh" #define NFORE 12 double Hist[],Fore[],Conf1[],Conf2[]; double Data[]; int NDat; CIndicatorES Es; int OnInit() { NDat=nHist; if(NDat<24)NDat=24; MqlRates rates[]; CopyRates(NULL,0,0,NDat,rates); ArrayResize(Data,NDat); SetIndexBuffer(0,Hist,INDICATOR_DATA); PlotIndexSetString(0,PLOT_LABEL,"History"); SetIndexBuffer(1,Fore,INDICATOR_DATA); PlotIndexSetString(1,PLOT_LABEL,"Forecast"); PlotIndexSetInteger(1,PLOT_SHIFT,NFORE); SetIndexBuffer(2,Conf1,INDICATOR_DATA); PlotIndexSetString(2,PLOT_LABEL,"ConfUp"); PlotIndexSetInteger(2,PLOT_SHIFT,NFORE); SetIndexBuffer(3,Conf2,INDICATOR_DATA); PlotIndexSetString(3,PLOT_LABEL,"ConfDN"); PlotIndexSetInteger(3,PLOT_SHIFT,NFORE); IndicatorSetInteger(INDICATOR_DIGITS,_Digits); return(0); } int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,start; double s,t,alp,gam,phi,e,f,a,a1,a2,a3,var,ci; if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);} if(prev_calculated==rates_total)return(rates_total); start=rates_total-NDat; PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat); PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE); PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE); PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE); for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; Es.CalcPar(Data); s=Es.GetPar(0); t=Es.GetPar(1); alp=Es.GetPar(2); gam=Es.GetPar(3); phi=Es.GetPar(4); f=(s+phi*t); var=0; for(i=0;i<NDat;i++) { e=Data[i]-f; var+=e*e; a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1; f=(s+phi*t); Hist[start+i]=f; } var/=(NDat-1); a1=1; a2=0; a3=1; for(i=rates_total-NFORE;i<rates_total;i++) { a1=a1*phi; a2+=a1; Fore[i]=s+a2*t; ci=1.96*MathSqrt(var*a3); a=alp*(1+a2*gam); a3+=a*a; Conf1[i]=Fore[i]+ci; Conf2[i]=Fore[i]-ci; } return(rates_total); }
В индикаторе при поступлении каждого нового бара происходит поиск оптимальных значений параметров модели, модель просчитывается для заданного числа NHist баров и строится прогноз и доверительные границы прогноза.
Единственным параметром индикатора является длина обрабатываемой последовательности, минимальное значение которой ограничивается на уровне 24 баров. Все расчеты в индикаторе производятся на основании значений open[]. Горизонт прогнозирования составляет 12 баров. Код индикатора IndicatorES.mq5 и файл CIndicatorES.mqh размещены в конце статьи в архиве Files.zip.
Рисунок 7. Результат работы индикатора IndicatorES.mq5
На рисунке 7 приведен пример работы индикатора IndicatorES.mq5. При работе индикатора, 95% доверительный интервал прогноза будет принимать значения, соответствующие найденным оптимальным величинам параметров модели. Чем больше значения параметров сглаживания, тем быстрее при увеличении горизонта прогноза увеличивается доверительный интервал.
При несложной доработке индикатор IndicatorES.mq5 может быть использован не только для прогнозирования непосредственно котировок валют, но и для построения прогноза значений различного рода индикаторов или предварительно подготовленных данных.
Заключение
Основной целью статьи было знакомство читателя с используемыми для прогнозирования аддитивными моделями экспоненциального сглаживания. В процессе демонстрации их практического применения были затронуты и некоторые сопутствующие вопросы. Однако представленные в статье материалы можно рассматривать лишь как первое прикосновение к огромному пласту связанных с прогнозированием проблем и решений.
Хочется обратить внимание на то, что приведенные в статье классы, функции, скрипты и индикаторы были созданы в процессе написания статьи и предназначены в первую очередь для использования в качестве иллюстрации к материалам статьи. Поэтому серьезного тестирования на устойчивость и отсутствие ошибок не производилось. Кроме того, приведенные в статье индикаторы следует рассматривать только как демонстрацию программной реализации рассматриваемых в статье методов.
Скорее всего, точность прогнозирования приведенного в статье индикатора IndicatorES.mq5 можно несколько увеличить, если использовать модификации применяемой модели, которые будут лучше учитывать особенности рассматриваемых котировок. Так же можно дополнить индикатор другими моделями. Но эти вопросы уже выходят за рамки данной статьи.
В завершении следует отметить, что модели экспоненциального сглаживания в определенных случаях в состоянии давать прогнозы, не уступающие по точности прогнозам, полученным при использовании более сложных моделей, при этом лишний раз подтверждая тот факт, что самая сложная модель далеко не всегда является самой лучшей.
Ссылки
- Everette S. Gardner Jr. Exponential smoothing: The state of the art – Part II. June 3, 2005.
- Rob J Hyndman. Forecasting based on state space models for exponential smoothing. 29 August 2002.
- Rob J Hyndman et al. Prediction intervals for exponential smoothing using two new classes of state space models. 30 January 2003.
- Rob J Hyndman and Muhammad Akram. Some nonlinear exponential smoothing models are unstable. 17 January 2006.
- Rob J Hyndman and Anne B Koehler. Another look at measures of forecast accuracy. 2 November 2005.
- Лукашин Ю.П., Адаптивные методы краткосрочного прогнозирования временных рядов: Учебное пособие. – М.: Финансы и статистика, 2003.-416 с.
- Химмельблау Д., Прикладное нелинейное программирование. М.: Мир, 1975.
- Numerical Recipes in C. The Art of Scientific Computing. SecondEdition. Cambridge University Press.
Экспоненциальное сглаживание
Экспоненциальное сглаживание
является одним из наиболее распространенных приемов, используемых для
сглаживания временных рядов, а также для прогнозирования. В основе процедуры
сглаживания лежит расчёт экспоненциальных скользящих средних сглаживаемого
ряда.
Главное достоинство прогнозной модели, основанной на экспоненциальных
средних, состоит в том, что она способна последовательно адаптироваться
к новому уровню процесса без значительного реагирования на случайные отклонения.
Исторически метод независимо был разработан Брауном и Холтом. Холт также
разработал модели экспоненциального сглаживания для процессов с постоянным
уровнем, процессов с линейным ростом и процессов с сезонными эффектами.
Процедура простого экспоненциального сглаживания осуществляется по следующим
формулам:
![]()
![]()
где:
-
Xt-1. Фактическое
наблюдение в момент t-1; -
St.
Значение экспоненциального среднего в момент t; -
α.
Параметр сглаживания, α = const, α ϵ (0; 1].
Экспоненциальное среднее в момент t
здесь выражено как взвешенная сумма текущего наблюдения и экспоненциального
среднего прошлого наблюдения с весами α
и (1 – α) соответственно.
Если последовательно использовать данное рекуррентное соотношение, то
значение St
можно выразить через значения временного ряда X:
![]()
Таким образом, величина St оказывается
взвешенной суммой всех членов ряда. Причем значения весов уменьшаются
экспоненциально в зависимости от удаленности наблюдения относительно момента
t. Это и объясняет название «экспоненциальное
среднее».
Экспоненциальное сглаживание можно представить как фильтр, на вход которого
в виде потока последовательно поступают члены исходного ряда, а на выходе
формируются значения экспоненциальных средних. Причем, сглаженный ряд
St
имеет тоже математическое ожидание, что и ряд X,
но меньшую дисперсию.
При высоком значении α дисперсия
сглаженного ряда не значительно отличается от дисперсии ряда X.
Чем меньше α, тем в большей степени
сокращается дисперсия сглаженного ряда (то есть подавляются колебания
исходного ряда).
Далее экспоненциальное среднее можно использовать для построения краткосрочных
прогнозов. В этом случае предполагается, что исходный ряд описывается
моделью:
![]()
где:
-
at.
Изменяющийся во времени средний уровень ряда; -
errt.
Случайные неавтокоррелированные отклонения с нулевым математическим
ожиданием.
Прогнозная модель имеет вид:
![]()
где:
-
 . Прогноз, сделанный
. Прогноз, сделанный
в момент T на τ единиц времени
(шагов) вперед; -
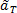 . Оценка aT.
. Оценка aT.
Оценкой параметра модели aT служит экспоненциальное
среднее ряда ST. Таким образом, все свойства экспоненциального
среднего распространяются на прогнозную модель. В частности, если привести
рекуррентную формулу к следующему виду:
![]()
и рассматривать St-1
как прогноз на один шаг вперед, то величина (Xt-1 – St-1) есть погрешность этого прогноза,
а новый прогноз St получается в результате корректировки
предыдущего прогноза с учетом его ошибки. В этом и состоит сущность адаптации.
На основе простого экспоненциального сглаживания были разработаны более
сложные модели сглаживания временных рядов, содержащих периодические сезонные
колебания и/или обладающих тенденцией роста.
Данная система позволяет строить наряду с простым экспоненциальным сглаживанием
модели, отражающие эффекты роста (линейного, экспоненциального или затухающего)
и сезонности (аддитивного или мультипликативного), которыми обладает исходный
ряд.
В общем виде рекуррентная формула экспоненциального сглаживания записывается
следующим образом:
![]()
где множители d1
и d2
определяются в зависимости от выбранной модели сглаживания. К примеру,
при простом экспоненциальном сглаживании, рассмотренном выше, d1 = Xt, d2 = St-1.
См. также:
Модель
с сезонными эффектами | Модели
роста | Метод наилучшей пробы
| Контейнер моделирования: модель «Экспоненциальное
сглаживание» | Анализ временных рядов: «Экспоненциальное
сглаживание» | IModelling.Expsmooth
| ISmExponentialSmoothing




![{displaystyle {begin{aligned}s_{t}&=alpha x_{t}+(1-alpha )s_{t-1}\[3pt]&=alpha x_{t}+alpha (1-alpha )x_{t-1}+(1-alpha )^{2}s_{t-2}\[3pt]&=alpha left[x_{t}+(1-alpha )x_{t-1}+(1-alpha )^{2}x_{t-2}+(1-alpha )^{3}x_{t-3}+cdots +(1-alpha )^{t-1}x_{1}right]+(1-alpha )^{t}x_{0}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08e0741e7160744aaff5c671b60bc05f0be172fb)





![{displaystyle {begin{aligned}a_{t}&=2s'_{t}-s''_{t}\[5pt]b_{t}&={frac {alpha }{1-alpha }}(s'_{t}-s''_{t}).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/496559e07c278001d2b3e1cf46743c3c4f9cae7c)
![{displaystyle {begin{aligned}s_{0}&=x_{0}\[5pt]s_{t}&=alpha {frac {x_{t}}{c_{t-L}}}+(1-alpha )(s_{t-1}+b_{t-1})\[5pt]b_{t}&=beta (s_{t}-s_{t-1})+(1-beta )b_{t-1}\[5pt]c_{t}&=gamma {frac {x_{t}}{s_{t}}}+(1-gamma )c_{t-L}\[5pt]F_{t+m}&=(s_{t}+mb_{t})c_{t-L+1+(m-1){bmod {L}}},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cee3212f28cf23aad40563caab52147a225fd2a8)




