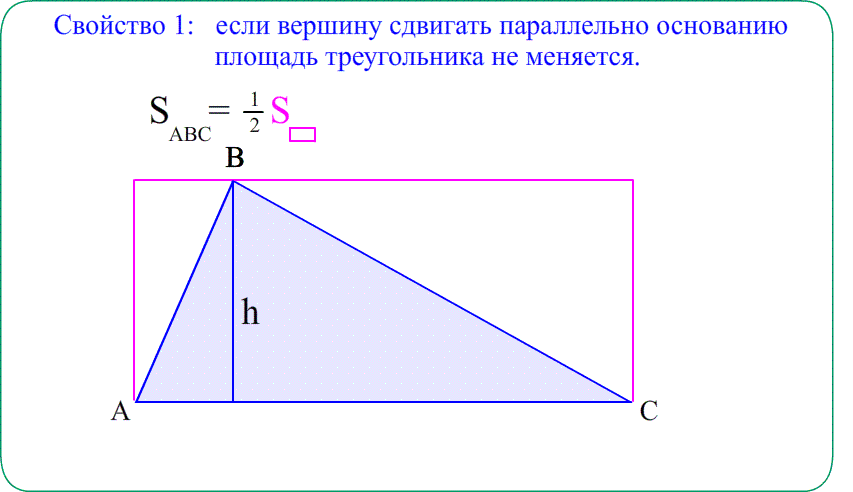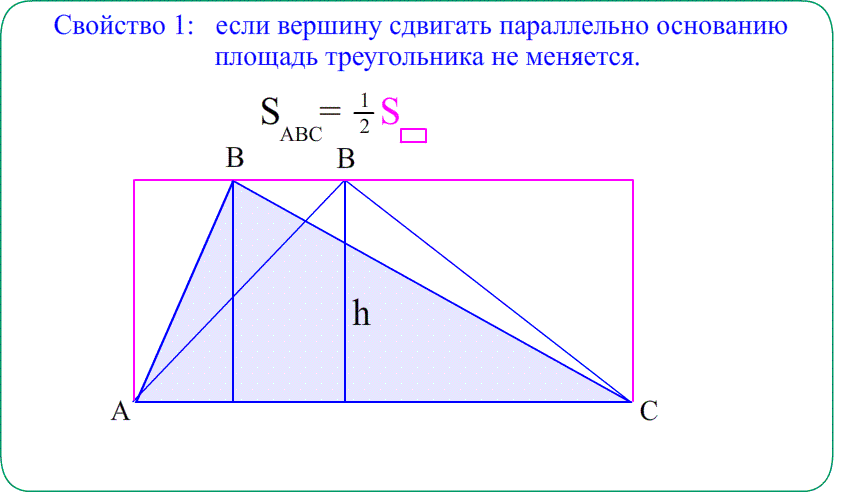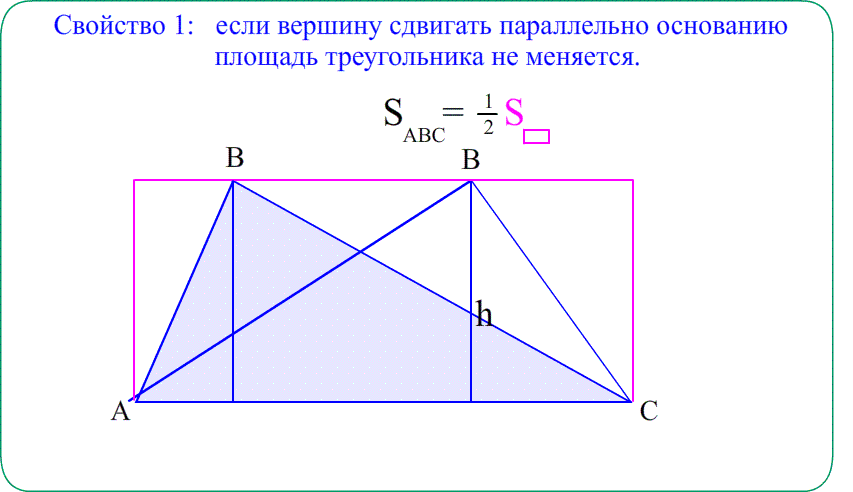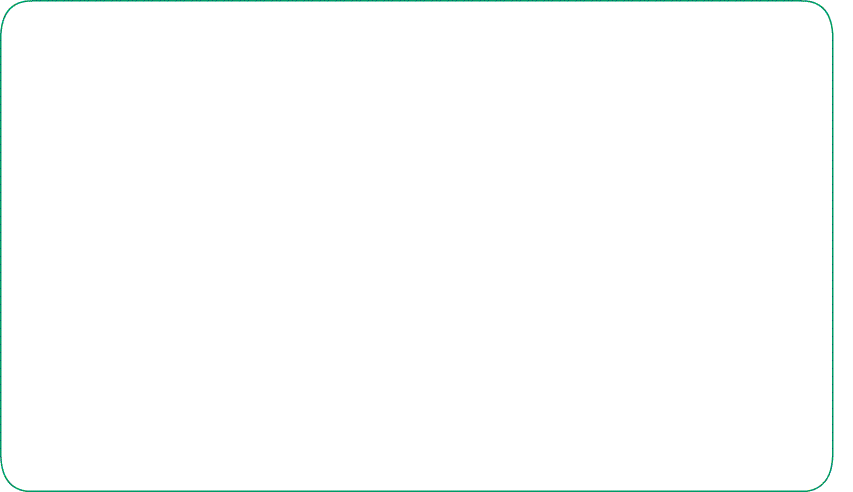
Всем привет, сегодня я покажу как выводятся 4-основные формулы для нахождения площади треугольника, для понимания следующего материала нужно знать теорему синусов, площадь прямоугольника.
*UDP доказательство формулы Герона в этой статье*
Для начала поймем один частный случай(если это понимаете, пролистывайте дальше).
Площадь прямоугольного треугольника.
У нас есть прямоугольный треугольник с катетами a,b, нужно найти его площадь.
Достраиваем до прямоугольника.
Площадь такого прямоугольника будет a * b, а значит площадь прямоугольного треугольника будет 1/2 * a * b(т.е. половинка от площади прямоугольника).
Этот факт нам понадобится для доказательства первой формулы.
Площадь треугольника через основание и высоту.
Мы опустили высоту на основание a, замечаем что исходный треугольник разбился на два прямоугольный треугольника, значит посчитаем их площадь, но для начала назовём отрезки x, y , на которые высота делит основание a.
Найдем площадь 1,2 треугольника и сложим их(т.к он и состоит из этих площадей).
А теперь вот здесь выносим общий множитель за скобку.
x + y – это и есть a, => получаем формулу половина основания на высоту.
Площадь через синус угла между сторонами.
Опустим высоту на основание b и назовём её x. Посмотрим на этот прямоугольный треугольник
Нам нужно найти x, как это можно сделать если нам известен только угол альфа и гипотенуза a? Очевидно, расписать синус этого угла и выразить от туда x.
Ну и теперь используем ранее доказанную формулу “половина основания на высоту”.
Произведение всех сторон на 4 радиуса описанной окружности.
Чтобы доказать эту формулу, нужно знать теорему синусов. и помнить ранее доказанную формулу.
Выразим синус угла альфа из теоремы синусов.
Подставляем синус альфа в ранее доказанную формулу.
Вот и вся формула. Изи, не правда ли? Теперь чуть посложнее.
Площадь треугольника через полупериметр и радиус вписанной окружности.
У нас есть треугольник ABC со сторонами a,b,c , в него вписана окружность радиуса r с центром O, которая касается сторон в точках K, L, M.
Проведём радиус в точки касания и соединим вершины треугольника с центром окр.
Теперь считаем площадь вот этих трех выделенных треугольников
Площадь AOC = 1/2 r * a, AOB = 1/2 r * b, COB = 1/2 r * c.
значит площадь ABC = AOC + AOB + COB
1/2 * r выносим за скобки.
(a + b + c )/ 2 это полупериметр p.
Вот и наша формула.
Если хотите узнать доказательство формулы Герона, заходите на эту статью.
Спасибо за внимание.
Учебник
Геометрия, 9 класс
Формулы площадей через синус угла
Основные свойства площадей фигур:
- Равные фигуры имеют равные площади. Две фигуры состоящие из одинаковых кусков – равновеликие.
- Аддитивность: Площадь фигуры, разрезанной на несколько частей, равна сумме площадей этих частей ;
- Площадь прямоугольника равна произведению ширины на длину … произведение сторон.
Задача 1: В параллелограмме известны стороны $7$, $10$ и синус угла между ними $frac{1}{2}$. Найти площадь параллелограмма.
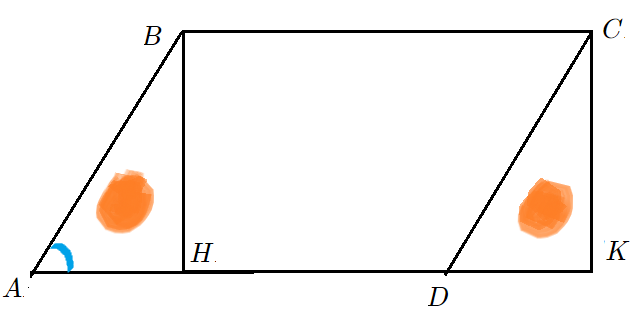
- Решение: Опустим высоты $BH$ и $CK$ на основание $AD$ . Они помогут “увидеть” площадь.
- Что есть синус $angle BAH$ в прямоугольном треугольнике $bigtriangleup ABH$? Отношение катета $BH$ к гипотенузе $AB$.
- Формула синуса позволит выразить высоту $BH$ через сторону $AB$ и синус $frac{1}{2}$. Высота $CK$ такая же.
- Параллелограмм $ABCD$ состоит из кусков: $bigtriangleup ABH$ и $4$-угольник $HBCD$. Площадь – сумма площадей кусков.
- Прямоугольник $HBCK$ состоит из кусков $HBCD$ и $bigtriangleup DCK$. Площадь также “сумма кусков”.
- Треугольники $bigtriangleup ABH$ и $bigtriangleup DCK$ одинаковые. Значит, параллелограмм и прямоугольник равновеликие.
- Площадь Параллелограмма $ABCD$ так же, как прямоугольника $HBCD$ равна высота на основание.
- $S_{ABCD}=S_{ABH}+S_{HBCD}=S_{HBCD}+S_{DCK}=S_{HBCK}=BHcdot HK=ABcdotsin angle BADcdot AD=7cdotfrac{1}{2}cdot10$
Теорема “о площади параллелограмма и треугольника через синус угла”:
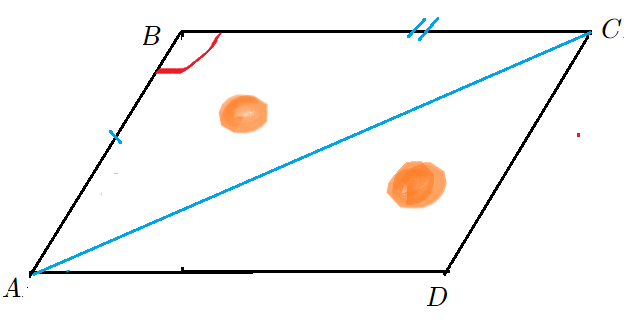
- Площадь параллелограмма равна произведению сторон на синус угла параллелограмма:
- Формулы $S=acdot bcdotsin angle BAD$ $S_{ABCD}=ABcdot BCcdotsin D$
- Площадь треугольника равна половине произведения сторон треугольника на синус угла между ними.
- Формулы $S=frac{1}{2}cdot acdot bcdotsin angle C$ $S_{bigtriangleup ABC}=frac{1}{2}cdot ABcdot BCcdotsin angle CBA$
Площадь треугольника также легко получить через площадь параллелограмма, равновеликого с двумя треугольниками, приставленными друг к другу по диагонали. Тогда площадь одного треугольника будет равна половине площади параллелограмма с тем же основанием и с той же высотой.
Задача 2: Диагонали четырехугольника делятся точкой пересечения на отрезки $3$, $5$ и $6$, $7$ . Синус угла между диагоналями $0,2$. Найти площади треугольников и всего четырехугольника.
- Дано: $BO=3$ $OD=5$ $CO=6$ $AO=7$ … угол между $sinangle AOB=0,2$. Найти: $S_{ABCD}=?$.
- Решение: Диагонали делят четырехугольник на 4 треугольника. Площадь = сумме 4-х площадей.
- Аддитивность: $S_{ABCD}=S_{bigtriangleup AOB}+S_{bigtriangleup BOC}+S_{bigtriangleup COD}+S_{bigtriangleup AOD}$.
- Площадь одного из них по формуле: $S_{bigtriangleup AOB}=frac{1}{2}cdot AOcdot OBcdot sin angle AOB=frac{1}{2}cdot 7 cdot 3cdot 0,2=2,1$
- Каковы синусы остальных углов? Свойство: Синусы смежных углов равны: $sinangle BOC=sinangle COD=sinangle AOD=0,2$
- Тогда, площади других треугольников $frac{1}{2}cdot 3 cdot 6cdot 0,2=1,8$ $frac{1}{2}cdot 6 cdot 5cdot 0,2=3$ $frac{1}{2}cdot 5 cdot 7cdot 0,2=3,5$
- Площадь четырехугольника равна сумме этих площадей Ответ: $S_{ABCD}=2,1+1,8+3+3,5=10,4$
Теоретически, по-другому: Распишем получение площади $S_{ABCD}$ в буквах, без числовых значений:
- $frac{1}{2}cdot OAcdot OBcdot sin angle AOB+frac{1}{2}cdot OBcdot OCcdot sin angle AOB+frac{1}{2}cdot OCcdot ODcdot sin angle AOB+frac{1}{2}cdot ODcdot OAcdot sin angle AOB$
- Вынос за скобки множителей $S_{ABCD}=frac{1}{2}cdot sin angle AOBcdot left(OAcdot OB+OBcdot OC+OCcdot OD+ODcdot OAright)$
- $S_{ABCD}=frac{1}{2}cdot sin angle AOBcdot left(OBcdotleft(OA+OCright)+ODcdotleft(OA+OCright)right)=frac{1}{2}cdot sin angle AOBcdot AC cdot (OB+OD)$
- Получаем $S_{ABCD}=frac{1}{2}cdot AC cdot BDcdot sin angle AOB$ $Rightarrow$ $S_{ABCD}=frac{1}{2}cdot (7+6) cdot (3+5)cdot 0,2=13cdot 0,8=10,4$

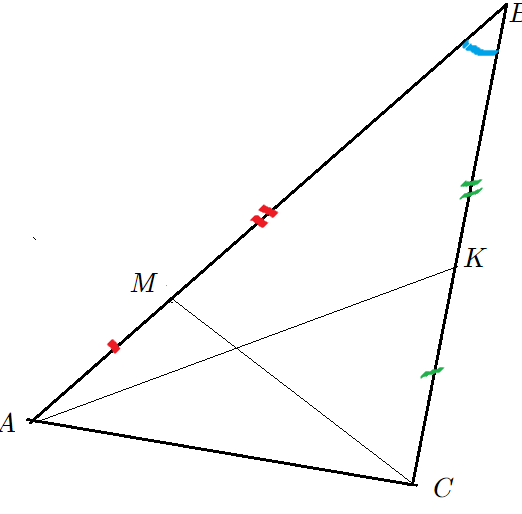
Задача 3: В треугольнике известны стороны $AB=10$ , $BC=12$ и угол $angle ABC=30$ . Точка $M$ делит сторону $AB$ в отношении 3 : 5, а точка $K$ делит сторону $BC$ в отношении 2 : 3. Найти площади и отношение площадей треугольников $ABK$ и $MBC$.
- Дано: $AB=10$, $BC=12$, $frac{AM}{MB}=frac{3}{5}$, $frac{BK}{KC}=frac{2}{3}$, $angle ABC=30$. Найти: $frac{S_{bigtriangleup ABK}}{S_{bigtriangleup MBC}}=?$
- Точка делит отрезок в известном соотношении. Находим части как систему уравнений $frac{x}{y}=?$ $x+y=?$
- $frac{AM}{MB}=frac{3}{5}$, аддитивность $AM+MB=AB=10$ $Rightarrow$ $frac{AM}{AB}=frac{3}{3+5}$ $Rightarrow$ $AM=frac{15}{4}$, $MB=frac{25}{4}$
- $frac{BK}{KC}=frac{2}{3}$, $BK+KC=12$ из свойств пропорций $BK=frac{24}{5}$, $KC=frac{36}{5}$
- Найдем площадь через синус $S_{bigtriangleup ABK}=frac{1}{2}cdot AB cdot BK cdot sin angle ABC = frac{1}{2}cdot 10 cdot frac{24}{5} cdot sin 30= 24 cdot 0,5=12$
- В треугольнике $MBC$ тот же угол, $S_{bigtriangleup MBC}=frac{1}{2}cdot MB cdot BC cdot sin angle ABC = frac{1}{2}cdot frac{25}{4} cdot 12 cdot 0,5=frac{75}{4}$
- отношение площадей треугольников $frac{S_{bigtriangleup ABK}}{S_{bigtriangleup MBC}}=frac{12}{frac{75}{4}}=frac{16}{25}$ Ответ: $frac{16}{25}$
Замечание, продолжение: Можно ли найти отношение площадей при неизвестных значениях сторон и угла?
- Зная лишь как делят точки $M$ и $K$ стороны треугольника, на какие пропорции ?!
- Дано только $frac{AM}{MB}=frac{3}{5}$, $frac{BK}{KC}=frac{2}{3}$. Выразим отрезки через стороны $AB$ и $BC$.
- Выразим площади $S_{bigtriangleup ABK}$ , $S_{bigtriangleup MBC}$ также через стороны $AB$ и $BC$ и угол $angle ABC$.
- Составим отношение площадей, выразим через стороны и угол. Что получится? Что можно сделать, ?
Теорема “о площади четырехугольника через диагонали и синус угла”:
- Площадь четырехугольника равна половине произведения диагоналей на синус угла между ними:
- Формулы $S=frac{1}{2}cdot d_1 cdot d_2 cdotsin angle alpha$ $S_{ABCD}=frac{1}{2}cdot AC cdot BDcdot sin angle AOB$
- Площадь ромба равна половине произведения диагоналей. … диагонали перпендикулярны!
- Формулы $S=frac{1}{2}cdot d_1 cdot d_2=frac{1}{2}cdot AC cdot BD$ $angle AOB=90$ $sin angle AOB=1$
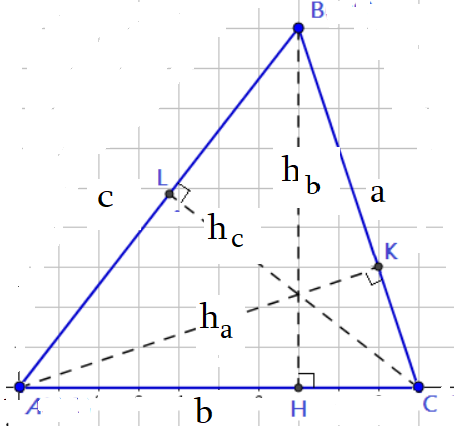
Формулы площади треугольника:
$S=frac{acdot h_a}{2}=frac{acdot bcdotsin C}{2}$ $S=frac{bcdot h_b}{2}=frac{bcdot ccdotsin A}{2}$ $S=frac{ccdot h_c}{2}=frac{ccdot acdotsin B}{2}$.
$sin A=frac{h_b}{c}=frac{h_c}{b}$ $sin B=frac{h_a}{c}=frac{h_c}{a}$ $sin C=frac{h_b}{a}=frac{h_a}{b}$.
$S_{ABC}=frac{1}{2}cdot ACcdot BCcdotsin C$ $S_{ABC}=frac{1}{2}cdot ABcdot BCcdotsin B$ $S_{ABC}=frac{1}{2}cdot ACcdot ABcdotsin A$ .
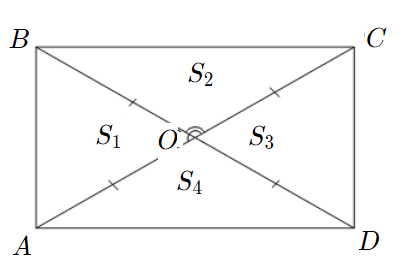
Задача 4: В прямоугольнике диагонали $10$ и угол между ними $30$. Найти площадь.
- Дано: $ABCD$ – прямоугольник , $AC=10$ , $angle AOB=30$ Найти: $S_{ABCD}$ .
- Решение: В прямоугольнике диагонали равны и пересекаются по середине $AO=OB=5$
- $bigtriangleup AOB$ и $bigtriangleup COD$ равные $Rightarrow$ $S_1=S_3$ ;
- $bigtriangleup BOC$ и $bigtriangleup AOD$ равные $Rightarrow$ $S_2=S_4$ .
- Смежные, $angle BOC=180-angle AOB=150$. Найдем отношение $frac{S_1}{S_2}=frac{frac{1}{2}AOcdot OBcdotsin30}{frac{1}{2}BOcdot OCcdotsin150}$
- $sin30=sinleft(180-30right)=sin150$. тогда $frac{S_1}{S_2}=frac{frac{1}{2}cdot5cdot5cdotsin150}{frac{1}{2}cdot5cdot5cdotsin150}=1$ Значит, $S_1=S_2$
- Аналогично: $frac{S_3}{S_4}=frac{frac{1}{2}DOcdot OCcdotsin30}{frac{1}{2}AOcdot ODcdotsin150} =1$ $Rightarrow$ $S_3=S_4$, площади равные.
- Диагонали рассекают прямоугольник на четыре равновеликих: треугольника $S_1=S_2=S_3=S_4$ .
- … тогда, по свойству аддитивности площадей $S_1=S_2=S_3=S_4=frac{1}{4}S_{ABCD}$ .
- $S_{AOB}=S_1=frac{1}{2}AOcdot OBcdot sin 30=frac{1}{2}cdot 5cdot 5cdot frac{1}{2}=frac{25}{4}$ $Rightarrow$ $S_{ABCD}=4cdotfrac{25}{4}$
- Найдя площадь АОВ, нашли площадь прямоугольника умножением на 4. Ответ: $S_{ABCD}=25$
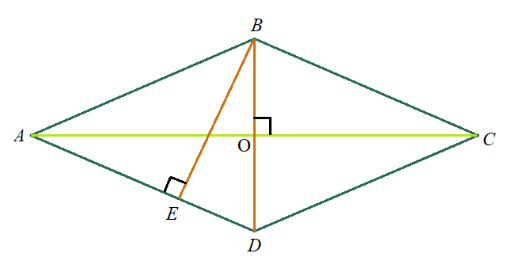
Задача 5: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Дано: ромб $ABCD$ , $BD=13$, высота $EB=12$ , Найти: $S_{ABCD}$ .
- Решение: прямоугольный $bigtriangleup BED$, подобен тем, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Одинаковый “состав” углов. Все прямоугольные,
- Прямоугольный $bigtriangleup BED$, по Пифагору выразим катет $DE=sqrt{BD^2-BE^2}=5$
- Диагонали в ромбе делятся пополам: $BO=OD=frac{BD}{2}=6,5$ $AO=frac{AC}{2}$ $AC=2cdot AO$
- Для нахождения площади ромба нам нужно найти вторую диагональ.
- $bigtriangleup BED sim bigtriangleup AOD$ $Rightarrow$ $frac{AO}{BE}=frac{OD}{ED}$ $Rightarrow$ $AO=frac{ODcdot BE}{ED}=frac{6,5cdot 12}{5}=15,6$ $AC=2cdot AO=31,2$
- Ответ: Площадь ромба через диагонали: $S_{ABCD}=frac{1}{2}cdot ACcdot BD=0,5cdot 31,2cdot13=202,8$


Задача 6. Площадь равнобедренного треугольника равна $100$ , а угол при вершине $30^o$ 1) Найти его боковые стороны . 2) Найти тригонометрию $15^o$
- Решение: 1) Известны площадь и угол, значит используем формулу площади через синус $30^o$ .
- Пусть боковая сторона $a$ , $S=frac{1}{2}acdot acdotsin30$ , тогда $100=frac{1}{2}a^2cdotsin30$ $Leftrightarrow$ $100=frac{1}{2}a^2cdotfrac{1}{2}$ $Rightarrow$
- $a=sqrt{400}=20$ Ответ: $a=20$
- 2) По теореме косинусов найдем основание $c=sqrt{a^2+a^2-2cdot acdot acdotfrac{sqrt{3}}{2}}=asqrt{2-sqrt{3}}$
- Из вершины равнобедренного угла проведем биссектрису к основанию. По свойству равнобедренности
- она будет и высотой $h$ (треугольник поделится на 2 прямоугольных с углами 15 градусов) и медианой,
- а значит основание поделится пополам , как и угол 30 у вершины поделится по 15 градусов.
- По прямоугольнему треугольнику (половинка): $sin15=frac{0,5cdot c}{a}=frac{0,5cdot acdotsqrt{2-sqrt{3}}}{a}=frac{sqrt{2-sqrt{3}}}{2}$
- Площадь через основание $S=frac{1}{2}cdot ccdot h$, найдем высоту $h=frac{2cdot S}{c}=frac{2cdot0,5cdot a^2cdotsin30}{acdotsqrt{2-sqrt{3}}}=frac{a}{2cdotsqrt{2-sqrt{3}}}$
- В прямоугольном треугольнике стороны $h$, $frac{c}{2}$, $a$. Тогда $cos15=frac{h}{a}=frac{frac{a}{2cdotsqrt{2-sqrt{3}}}}{a}=frac{1}{2cdotsqrt{2-sqrt{3}}}$
Интерактивные Упражнения
Площадь прямоугольного треугольника
Ирина Алексеевна Антоненко
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
На этой странице вы узнаете, как вычислить площадь прямоугольного треугольника, также здесь вы найдёте онлайн-калькуляторы для вычисления площади прямоугольного треугольника по различным заданным величинам.
Определение 1
Прямоугольный треугольник — это треугольник, один из углов которого является прямым, при этом два другие угла — острые.
Для того чтобы воспользоваться приведёнными онлайн-калькуляторами для расчётов, введите известные величины.
Одной из самых простых формул для вычисления площади прямоугольного треугольника является формула через катеты.
Площадь прямоугольного треугольника по двум катетам

Формула площади прямоугольного треугольника по двум катетам выглядит как:
$S = frac12 cdot a cdot b$, где
$S$ – площадь треугольника,
$a$ – первый катет данного треугольника,
$b$ – второй катет данного треугольника.
Пример 1
Задача
Дан прямоугольный треугольник, две меньшие стороны которого равны $3$ и $4$. Чему равна его площадь?
Решение:
Самой длинной стороной в треугольнике является гипотенуза, поэтому воспользуемся формулой вычисления площади через катеты:
$S = frac12 cdot a cdot b = frac12 cdot 3 cdot 4 = 6$.
Ответ: $6$.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Также площадь прямоугольного треугольника можно вычислить если известна гипотенуза и угол между гипотенузой и одним из катетов.
Площадь прямоугольного треугольника по гипотенузе и углу

Площадь прямоугольного треугольника через гипотенузу можно найти по формуле для площади треугольника через 2 стороны и синус угла между ними:
$S = frac12 cdot a cdot c cdot sin (α)$ (1).
Для начала необходимо найти одну из его сторон.
Для этого вспомним определение косинуса:
$cos (α) = frac{a}{c}$.
Из него выразим сторону $a$:
$a = c cdot cos (α)$.
Подставим $a$ в формулу (1):
$S = frac12 c^2 cdot cos (α) cdot sin (α)$, здесь
$c$ — гипотенуза;
$α$ — угол между сторонами $a$ и $c$.
Пример 2
Задача
Гипотенуза прямоугольного треугольника равна $7$, а угол $α$ между гипотенузой и катетом $a$ равен $30°$. Найдите, чему равна площадь треугольника.
Решение:
Найдём сторону $a$:
$a = c cdot cos (30°) ≈ 7 cdot 0.866 ≈ 6.06$
Подставим полученное значение для вычисления площади треугольника через синус угла:
$S = frac12 cdot a cdot c cdot sin (α) = frac12 cdot 6.06 cdot 7 cdot 0.5 = 10.605$.
Ответ: $10.605$.
Другим способом вычисления площади прямого треугольника является вычисление через формулу Герона.
Площадь прямоугольного треугольника по формуле Герона

Рассчитать площадь прямоугольного треугольника по формуле Герона можно следующим образом:
$S = (p – a) cdot (p – b)$, где
$S$ – площадь треугольника,
$a$ – первый катет,
$b$ – второй катет,
$p$ – полупериметр данного треугольника, вычисляемый по формуле:
$p = frac{a + b + c}{2}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 10.06.2019
Площадь треугольника через синус угла
Если вам необходимо вычислить площадь треугольника через синус угла, тогда вы зашли именно по адресу, потому что сегодня мы детально изучим этот вопрос.
Подобный род задач достаточно распространен в геометрии и, несмотря на свою простоту, неправильное использование формулы может привести к неверному результату.
В общем случае площадь треугольника можно вычислить по формуле: половина произведения двух сторон на синуса угла между ними.
Формулы площади треугольника через синус угла:
Схематическое изображение треугольника:

Где b, с, а – стороны треугольника;
γ, α, β – углы между сторонами.

Если известна только одна сторона и величины всех трех углов, тогда площадь можно найти как:

Площадь равнобедренного треугольника через синус:

здесь a = c,
β – угол между a и c,
α – угол между a и b.
Как можно было увидеть вышеуказанная формула ничем не отличается от общей.
Площадь прямоугольного треугольника через синус:


Где а,b,с – стороны треугольника
А,В,С – углы между сторонами.
Пример задачи
Рассмотрим задачу, в которой известно размеры двух сторон треугольника, а также величина угла между ними. Таким образом, мы можем определить площадь треугольника, которая находится как половина произведения двух сторон и синуса угла между ними.
Площадь треугольника через синус угла
Если вам необходимо вычислить площадь треугольника через синус угла, тогда вы зашли именно по адресу, потому что сегодня мы детально изучим этот вопрос.
Подобный род задач достаточно распространен в геометрии и, несмотря на свою простоту, неправильное использование формулы может привести к неверному результату.
В общем случае площадь треугольника можно вычислить по формуле: половина произведения двух сторон на синуса угла между ними.
Формулы площади треугольника через синус угла:
Схематическое изображение треугольника:
Где b, с, а – стороны треугольника;
γ, α, β – углы между сторонами.
Если известна только одна сторона и величины всех трех углов, тогда площадь можно найти как:
Площадь равнобедренного треугольника через синус:
Как можно было увидеть вышеуказанная формула ничем не отличается от общей.
Площадь прямоугольного треугольника через синус:
Где а,b,с – стороны треугольника
А,В,С – углы между сторонами.
Пример задачи
Рассмотрим задачу, в которой известно размеры двух сторон треугольника, а также величина угла между ними. Таким образом, мы можем определить площадь треугольника, которая находится как половина произведения двух сторон и синуса угла между ними.
Площадь треугольника через синус
Определение
Площадь треугольника через синус — это площадь треугольника,
выраженная через две любые стороны треугольника и синус угла между ними.
Синус угла — это число, которое используется для нахождения
разных величин в треугольниках, его можно найти в специальных таблицах.
Введение
Площадь треугольника кроме половины произведения высоты
на основания, можно также найти и другим способом.
Мало кто знает, но через синусы углов можно найти обычно
не только стороны, но и площадь любого треугольника!
Площадь треугольника выраженная без синуса численно равна
половине произведения двух сторон друг на друга
на синус угла между ними.
Площадь треугольника через синус ищется только в том случае,
если по другой формуле площадь треугольника найти нельзя.
Теорема
( S = frac<1>2 * BC * AC * sin angle BCA )
Площадь произвольного треугольника равна полусумме
произведения двух любых сторон треугольника друг на друга,
и на синус угла между этими сторонами.
Формула
[ S = frac<1>2 * a * b * sin α ]
Где a, b — две стороны треугольника, синус α — синус угла α.
Пример
Для примера, возьмем треугольник omk, изображенный на рисунке 1, со сторонами om, mk, ok.
Известно, что mk равен 6, ok равен 8, синус угла okm равен 1/4.
Нужно найти площадь треугольника omk.
Дано: △omk, mk = 6, ok = 8, sin okm = 1/4.
Найти: S △omk — ?
Решение:
1) ( S = frac<1>2*a*b*sin α ) ( implies ) ( S = frac<1>2*mk*ok*sin okm )
2) S = 1/2 * 6 * 8 * 1/4 = 1/2 * 6 * 8 * 0.25 = 1/2 * 48 * 0.25 = 1/2 * 12 = 6
Ответ: Площадь треугольника omk равна 6.
Доказательство
Докажем, что площадь произвольного треугольника
равна полусумме произведения двух любых сторон
друг на друга, и на синус угла между этими сторонами.
Чтобы вам наглядно было видно, как мы доказываем,
используем один из известнейших треугольников — египетский треугольник.
Высота в египетском треугольнике равна длине одного из катетов.
Построим прямоугольный треугольник, изображенный на рисунке 2,
со сторонами 3,4,5 с одним из углов 90 градусов.
Первым делом найдем площадь обычной формулой,
затем с помощью синуса. Площадь равна половине
основания на высоту — ½3*4 = 6. Теперь найдем с
помощью синуса: ½3*4*sin90 = 6 * 1 = 6. Как видим,
полученные значения площадей сходятся, соответственно
через синус можно найти площадь треугольника ч.т.д.
Теперь, чтобы найти площадь треугольника нам не нужно
знать основание и высоту, можно знать только
две стороны и синус угла между ними.
Заключение
В заключение, можно сказать, что площадь
треугольника можно найти разными способами.
Например, в прямоугольном треугольнике площадь
рассчитать легче чем в любом другом треугольнике,
так как высота уже известна. Именно поэтому,
в школьном курсе, отчасти так подробно изучаются
прямоугольные треугольники. В Древнем Египте были
распространены прямоугольные треугольники со
сторонами 3,4,5; 6,8,10; 5,12,13. Длины этих прямоугольных
треугольников треугольников целые, что значительно,
упрощало разного рода вычисления.
Формулу площади треугольника делает универсальной то,
что она может применена к абсолютно любым треугольникам.
Главное, чтобы были известные две стороны,
и угол или синус угла между ними.
Формула площади треугольника через синус — универсальна,
поэтому может быть применена к любым видам треугольников.
Как найти площадь треугольника
О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
[spoiler title=”источники:”]
http://colibrus.ru/ploschad-treugolnika-cherez-sinus-ugla-i-dve-storony/
http://skysmart.ru/articles/mathematic/ploshad-treugolnika
[/spoiler]