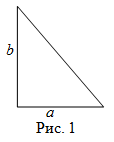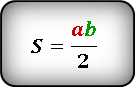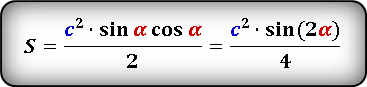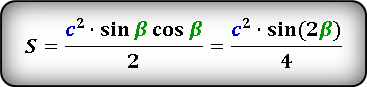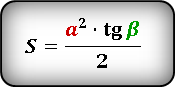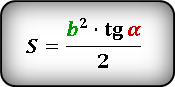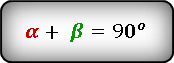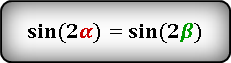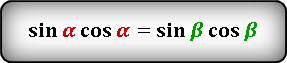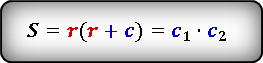Содержание:
- Формула
- Примеры вычисления площади прямоугольного треугольника
Формула
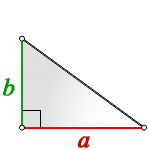
Чтобы найти площадь прямоугольного треугольника $ABC$ (рис. 1),
надо найти произведение катетов
$a$ и
$b$ и поделить его на два. То есть
$$mathrm{S}_{Delta A B C}=frac{a b}{2}$$
Напомним, что катетами прямоугольного треугольника называются стороны, которые пересекаются под прямым углом.
Примеры вычисления площади прямоугольного треугольника
Пример
Задание. Найти площадь прямоугольного треугольника
$ABC$, если известно, что длины его катетов равны 3 см и 4 см.
Решение. Искомая площадь равна половине произведения катетов, то есть
$mathrm{S}_{Delta A B C}=frac{3 cdot 4}{2}=frac{12}{2}=6$ (см2)
Ответ. $mathrm{S}_{Delta A B C}=6$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить площадь прямоугольного треугольника, один из катетов которого равен 6 см, а гипотенуза 10 см.
Решение. Искомая площадь равна половине произведения катетов. Используя теорему Пифагора,
найдем второй катет заданного треугольника:
$b=sqrt{10^{2}-6^{2}}=sqrt{100-36}=sqrt{64}=8$ (см)
Тогда площадь
$S=frac{6 cdot 8}{2}=frac{48}{2}=24$ (см2)
Ответ. $S=24$ (см2)
Читать дальше: как найти площадь равнобедренного треугольника.
Найти площадь прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Найти площадь прямоугольного треугольника
Чтобы посчитать площадь прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- длины катетов a и b
- длину гипотенузы с и длину любого из катетов (a или b)
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- длину гипотенузы с и один из острых углов (α или β)
Найти площадь прямоугольного треугольника по двум катетам
Катет a =
Катет b =
S =
0
Просто введите длины двух катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?
Формула
S = ½ ⋅ a ⋅ b
Пример
К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:
S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²
Найти площадь прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет (a или b) =
S =
0
Введите длины гипотенузы и одного из катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?
Формула
S = ½ ⋅ a ⋅ √c² – a² = ½ ⋅ b ⋅ √c² – b²
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:
S = 2 ⋅ √5² – 2² / 2 = √25 – 4 ≈ 4.58 см²
Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) = °
S =
0
Введите длину одного из катетов и прилежащий к нему острый угол в градусах.
То есть к катету a прилежащий ∠β, а к катету b – ∠α
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:
S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²
Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) = °
S =
0
Введите длину одного из катетов и противолежащий к нему острый угол в градусах.
То есть к катету a противолежащий ∠α, а к катету b – ∠β
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(90 – α) = ½ ⋅ b² ⋅ tg(90 – β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:
S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²
Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов
Гипотенуза c =
Угол (α или β) = °
S =
0
Введите длину гипотенузы и один из острых угол в градусах.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?
Формула
S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:
S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²

Формула:
S
=
1
2
ab
Где: a, b – стороны.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
1
4
С2
·sin(2α)
Где: C – гипотенуза, α – острый угол.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
1
2
a2
·tg(α)
Где: a – катет, α – острый угол.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
R·(R+C)
Где: С – гипотенуза, R – радиус вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
D
2
·(
D
2
+ C
)
Где: С – гипотенуза, D – диаметр вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
S
π
·(
S
π
+ C
)
Где: С – гипотенуза, S – площадь вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
P
2π
·(
P
2π
+ C
)
Где: С – гипотенуза, P – длина вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
C1
·
C2
Где: C1 , C2 – части гипотенузы.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
1
2
ch
Где: c – гипотенуза, h – высота.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано
Площадь треугольника равна половине произведения гипотенузы и высоты.
Содержание материала
- Площадь прямоугольного треугольника по формуле Герона
- Видео
- Площадь прямоугольного треугольника по катету и противолежащему углу
- Если он равносторонний
- Формула для нахождения площади прямоугольного треугольника через катеты
- Если известны длины трех сторон
- Как найти площадь равностороннего треугольника
Площадь прямоугольного треугольника по формуле Герона

Для вычисления площади треугольника применяются различные формулы, в зависимости от известных исходных данных. Выше приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления. Приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.
Наш калькулятор для вычисления площади поможет вам вычислить площадь разных видов треугольников или проверить уже выполненные вычисления.
В зависимости от вида треугольника и его известных исходных данных, площадь треугольника можно вычислить по различным формулам.
Видео
Площадь прямоугольного треугольника по катету и противолежащему углу
Пусть в прямоугольном треугольнике известны катет a и противолежащий угол α (Рис.5):
Найдем площадь прямоугольного треугольника. Коангенс угла α прямоугольного треугольника равна:

Откуда
 . . |
(12) |
Подставляя (12) в (1), получим формулу площади прямоугольного треугольника по катету и противожащему углу:
 . . |
(13) |
Пример 5. Известны катет и противолежащий угол прямоугольного треугольника: 
Решение. Для вычисления площади треугольника воспользуемся формулой (13). Подставляя значения 
Ответ:
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.
Формула для нахождения площади прямоугольного треугольника через катеты
Чтобы найти площадь, нужно вывести формулу:
Так как в прямоугольном треугольнике катеты перпендикулярны, то один катет — это высота, проведенная ко второму катету.
Отсюда следует, что площадь прямоугольного треугольника равна половине произведения его катетов.
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через катеты.
S = 1/2 (a × b), где a и b — катеты
Если известны длины трех сторон
Делайте так:
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Как найти площадь равностороннего треугольника
- Умножьте квадрат стороны треугольника на корень из трёх.
- Поделите результат на четыре.
- S — искомая площадь треугольника.
- a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.
- 7 причин полюбить математику
- ТЕСТ: Помните ли вы геометрию?
- 10 хитрых головоломок со спичками для тренировки воображения
- Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
- ТЕСТ: Сможете ли вы решить простые математические примеры?
Теги
Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется – гипотенуза
1. Если известны только катеты
a, b – катеты треугольника
Формула площади треугольника через катеты ( S ) :
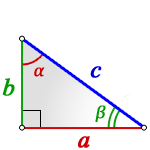
2. Если известны острый угол и гипотенуза или катет
c – гипотенуза
a, b – катеты
α, β – острые углы
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если
то справедливы следующие тождества:
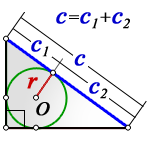
3. Если известны радиус вписанной окружности и гипотенуза
c – гипотенуза
c1, c2 – отрезки полученные делением гипотенузы, точкой касания окружности
r – радиус вписанной окружности
О – центр вписанной окружности
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :
- Подробности
-
Опубликовано: 07 сентября 2011
-
Обновлено: 13 августа 2021