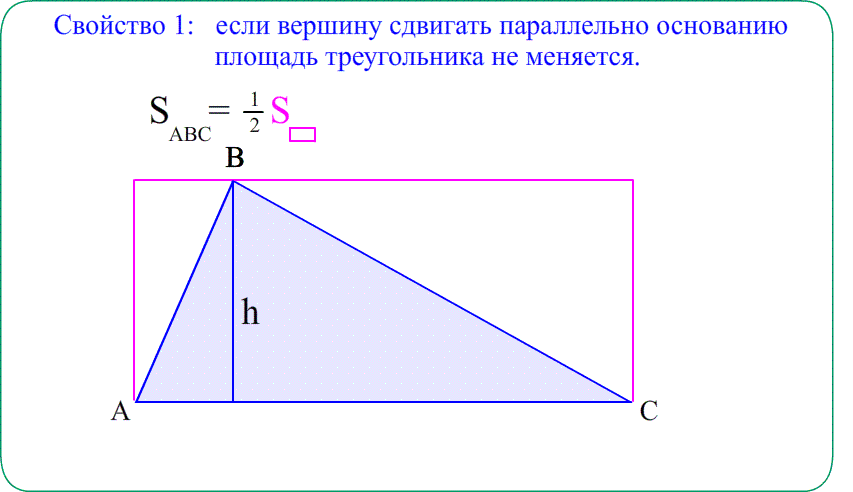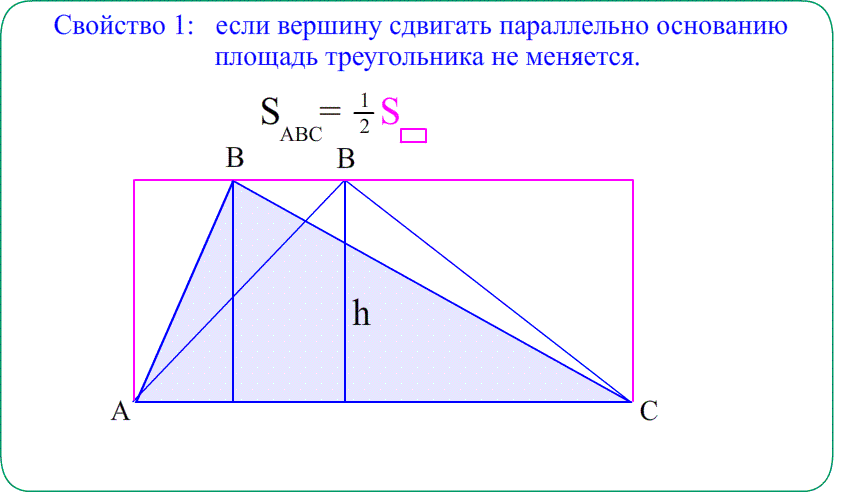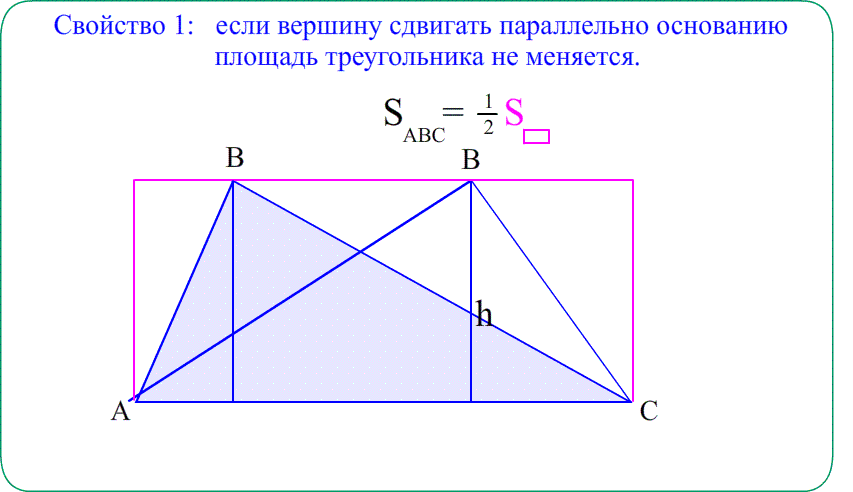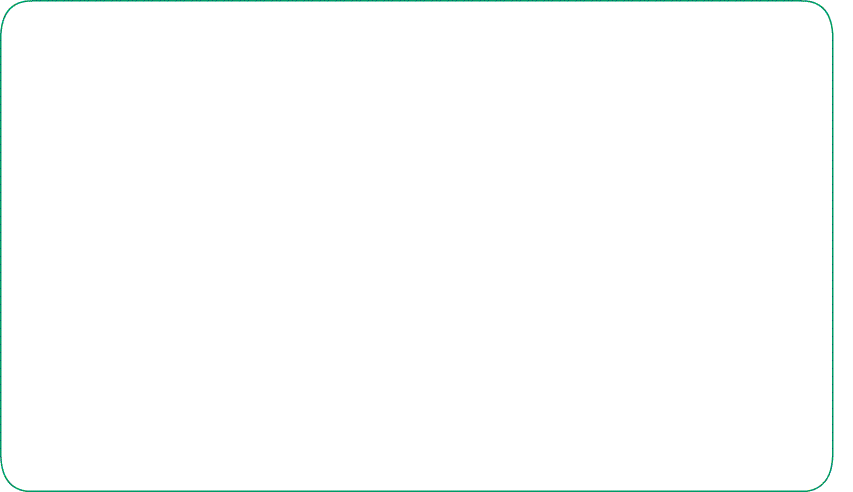
Площадь равнобедренного треугольника важна для вычисления многих геометрических и математических задач. Например, определение площади любого многоугольника связано с его разделением на ряд треугольников и расчетом площади каждого из них.
Геометрическое тело, обладающее двумя равными сторонами и углами – есть частный случай простого разностороннего многоугольника.
Каждая из идентичных линий называется боковой, а третья – основанием.
Если в таком треугольнике опустить среднюю линию из его вершины на 3-ю сторону, то образовавшиеся два плоских тела будут идентичны (так как имеют все признаки подобия).
Площадь (S) фигуры с тремя углами возможно установить:
-
по двум сторонам и высоте;
-
через угол между двумя сторонами и величину одной из них;
-
по двум сторонам;
-
через синус противолежащего основанию угла;
-
зная синус прилежащего угла и др.
Площадь равнобедренного треугольника через высоту
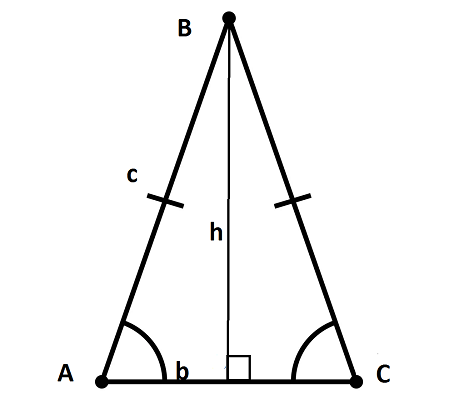
Вычисление площади треугольника с использованием его высоты и параметров основания – самый актуальный вариант, на базе которого строятся многие другие методы решения.
У планиметрической фигуры с двумя тождественными углами и боковыми отрезками высота может рассматриваться, как медиана и биссектриса. То есть линия, проведенная из вершины, делит планиметрический объект на два эквивалентных прямоугольных треугольника.
И общая их площадь сводится к:
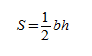
где:
-
b – размер основания;
-
h – высота.
Задача №1.
Требуется рассчитать S тупоугольного равнобедренного многоугольника. Его h=3 см, а длина b = 8 см.
Вычисления выглядят следующим образом:
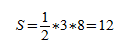
Ответ: 12 см2.
Площадь равнобедренного треугольника через стороны
Найти S планиметрического тела с двумя одинаковыми чертами, зная их параметры, возможно.
Для этого необходима теорема Пифагора, формулы которой видны на картинке,
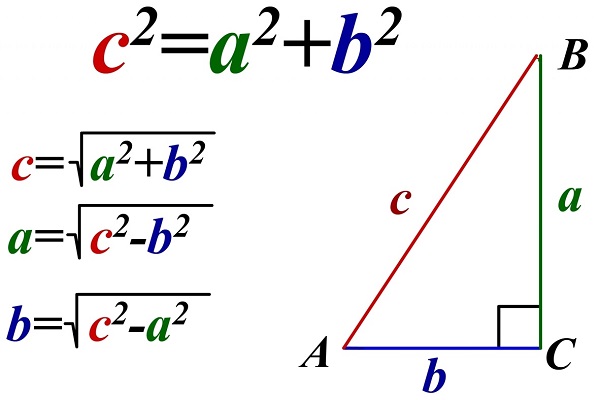
и формула для отыскания S через биссектрису S = ½ * b * h.
После проведения медианы к середине 3-его отрезка, в равнобедренном треугольнике образуются 2 единообразных плоских тела с h между 2-мя катетами.
Таким образом, используя свойство сторон прямоугольного треугольника, выводим формулу, которая показана на картинке:
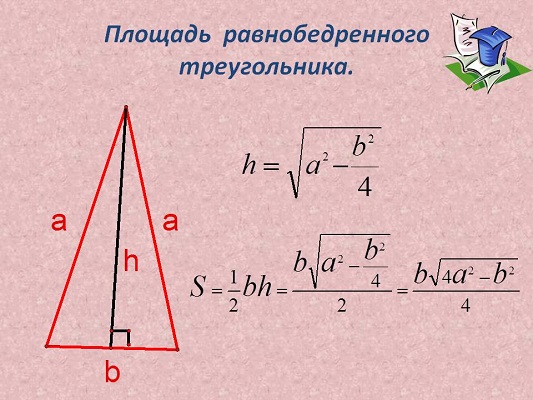
При высчитывание S равностороннего треугольника это выражение примет другой вид. Сравнить формулы нахождения площади равностороннего и равнобедренного треугольников можно, взглянув на картинку:
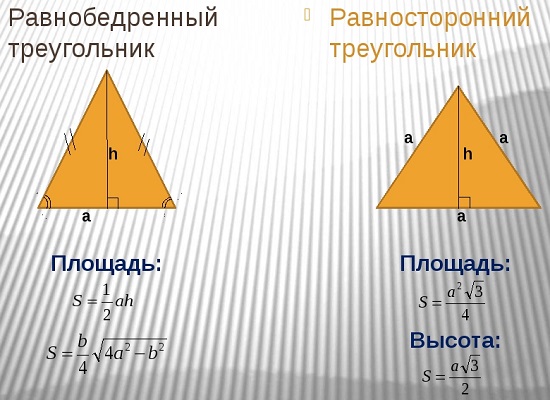
Задача №2.
У остроугольного равнобедренного треугольника даны габариты боковины b = 3 см и базиса a = 2 см. Надлежит найти его S:
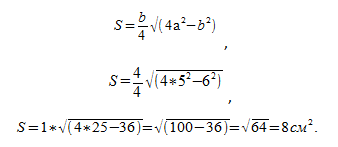
Ответ: 8 см2.
Площадь равнобедренного треугольника через синус угла
В геометрии встречаются задания по отысканию площади многоугольника с тремя схожими краями через данный угол и длину прилегающей стороны.
В этой ситуации определение размера h будет осуществляться с использованием угла, прилегающего к измеренной грани. Таким образом выводится выражение, которое хорошо иллюстрирует следующая картинка:
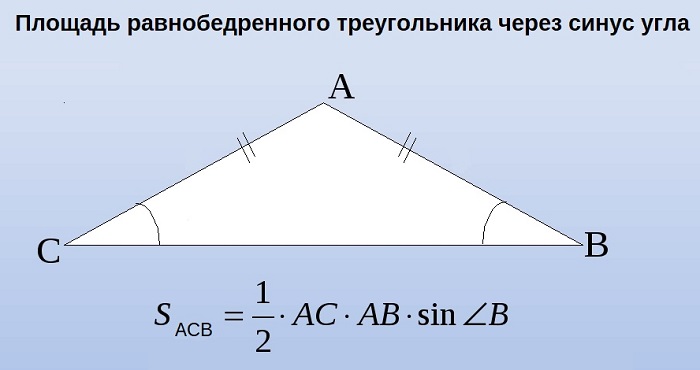
Задача №3.
Посмотрим на рисунок, приведенный выше. Известно, что ∠ACB фигуры 30 градусов, а величина его боковой стороны AC = AB равняется 4 см. Требуется вычислить её S.
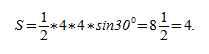
Ответ: 4 см2.
Формула площади равнобедренного треугольника через тангенс угла
Как правило, в планиметрии нередко встречаются задания по нахождению S треугольника, в котором определено значение стороны и угол.
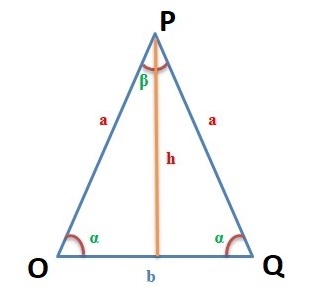
Рисунок 1
Разнообразные равенства для решения задач, в том числе и нахождения S через тангенс угла, можно увидеть ниже:
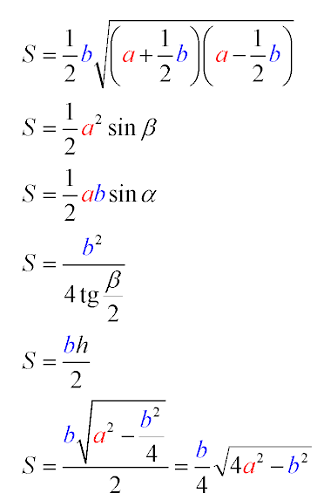
Задача №4.
Дан равнобедренный треугольник OPQ (см. рис. 1). Известны величины: основание OQ = 5 см и угол QOP = 450. Требуется найти площадь треугольника OPQ.
Прежде всего посмотрим, как найти нам требуемую величину и какую применить формулу. Остановим свой выбор на формуле нахождения площади S по тангенсу угла.
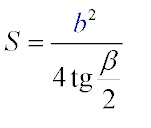
Зная, что у нас равнобедренный треугольник, у которого углы у основания равны, найдем третий угол:
180 — 45 — 45 = 900 — угол OPQ.
Вычисляем SOPQ:
SOPQ = 52/4 * tg 45° = 25/4 * 1 = 6, 25 см2
Ответ: 6,25 см2.
Вот так, используя прежде всего знания о свойствах фигур, можно получать самые разнообразные способы вычисления той величины, какая требуется в задаче.
Площадь равнобедренного треугольника – формулы вычисления
Площадь равнобедренного треугольника важна для вычисления многих геометрических и математических задач. Например, определение площади любого многоугольника связано с его разделением на ряд треугольников и расчетом площади каждого из них.
Геометрическое тело, обладающее двумя равными сторонами и углами – есть частный случай простого разностороннего многоугольника.
Каждая из идентичных линий называется боковой, а третья – основанием.

Если в таком треугольнике опустить среднюю линию из его вершины на 3-ю сторону, то образовавшиеся два плоских тела будут идентичны (так как имеют все признаки подобия).
Площадь (S) фигуры с тремя углами возможно установить:
по двум сторонам и высоте;
через угол между двумя сторонами и величину одной из них;
по двум сторонам;
через синус противолежащего основанию угла;
зная синус прилежащего угла и др.
Площадь равнобедренного треугольника через высоту
Вычисление площади треугольника с использованием его высоты и параметров основания – самый актуальный вариант, на базе которого строятся многие другие методы решения.
У планиметрической фигуры с двумя тождественными углами и боковыми отрезками высота может рассматриваться, как медиана и биссектриса. То есть линия, проведенная из вершины, делит планиметрический объект на два эквивалентных прямоугольных треугольника.
И общая их площадь сводится к:
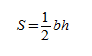
b – размер основания;
Требуется рассчитать S тупоугольного равнобедренного многоугольника. Его h=3 см, а длина b = 8 см.
Вычисления выглядят следующим образом:
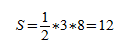
Площадь равнобедренного треугольника через стороны
Найти S планиметрического тела с двумя одинаковыми чертами, зная их параметры, возможно.
Для этого необходима теорема Пифагора, формулы которой видны на картинке,
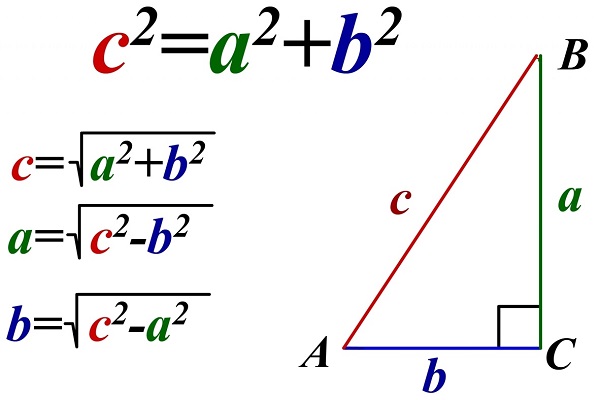
и формула для отыскания S через биссектрису S = ½ * b * h.
После проведения медианы к середине 3-его отрезка, в равнобедренном треугольнике образуются 2 единообразных плоских тела с h между 2-мя катетами.
Таким образом, используя свойство сторон прямоугольного треугольника, выводим формулу, которая показана на картинке:

При высчитывание S равностороннего треугольника это выражение примет другой вид. Сравнить формулы нахождения площади равностороннего и равнобедренного треугольников можно, взглянув на картинку:

У остроугольного равнобедренного треугольника даны габариты боковины b = 3 см и базиса a = 2 см. Надлежит найти его S:
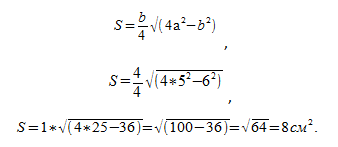
Площадь равнобедренного треугольника через синус угла
В геометрии встречаются задания по отысканию площади многоугольника с тремя схожими краями через данный угол и длину прилегающей стороны.
В этой ситуации определение размера h будет осуществляться с использованием угла, прилегающего к измеренной грани. Таким образом выводится выражение, которое хорошо иллюстрирует следующая картинка:

Посмотрим на рисунок, приведенный выше. Известно, что ∠ACB фигуры 30 градусов, а величина его боковой стороны AC = AB равняется 4 см. Требуется вычислить её S.
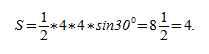
Формула площади равнобедренного треугольника через тангенс угла
Как правило, в планиметрии нередко встречаются задания по нахождению S треугольника, в котором определено значение стороны и угол.

Разнообразные равенства для решения задач, в том числе и нахождения S через тангенс угла, можно увидеть ниже:
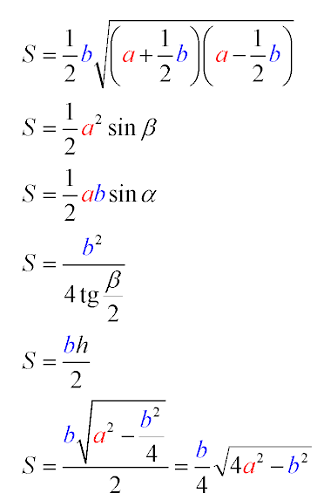
Дан равнобедренный треугольник OPQ (см. рис. 1). Известны величины: основание OQ = 5 см и угол QOP = 45 0 . Требуется найти площадь треугольника OPQ.
Прежде всего посмотрим, как найти нам требуемую величину и какую применить формулу. Остановим свой выбор на формуле нахождения площади S по тангенсу угла.
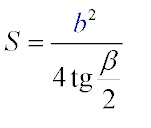
Зная, что у нас равнобедренный треугольник, у которого углы у основания равны, найдем третий угол:
180 — 45 — 45 = 90 0 — угол OPQ.
SOPQ = 5 2 /4 * tg 45° = 25/4 * 1 = 6, 25 см 2
Вот так, используя прежде всего знания о свойствах фигур, можно получать самые разнообразные способы вычисления той величины, какая требуется в задаче.
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Площадь треугольника через синус

Определение
Площадь треугольника через синус — это площадь треугольника,
выраженная через две любые стороны треугольника и синус угла между ними.
Синус угла — это число, которое используется для нахождения
разных величин в треугольниках, его можно найти в специальных таблицах.
Введение
Площадь треугольника кроме половины произведения высоты
на основания, можно также найти и другим способом.
Мало кто знает, но через синусы углов можно найти обычно
не только стороны, но и площадь любого треугольника!
Площадь треугольника выраженная без синуса численно равна
половине произведения двух сторон друг на друга
на синус угла между ними.
Площадь треугольника через синус ищется только в том случае,
если по другой формуле площадь треугольника найти нельзя.
Теорема
( S = frac<1>2 * BC * AC * sin angle BCA )
Площадь произвольного треугольника равна полусумме
произведения двух любых сторон треугольника друг на друга,
и на синус угла между этими сторонами.
Формула
[ S = frac<1>2 * a * b * sin α ]
Где a, b — две стороны треугольника, синус α — синус угла α.
Пример
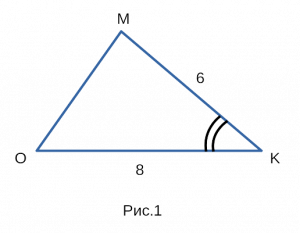
Для примера, возьмем треугольник omk, изображенный на рисунке 1, со сторонами om, mk, ok.
Известно, что mk равен 6, ok равен 8, синус угла okm равен 1/4.
Нужно найти площадь треугольника omk.
Дано: △omk, mk = 6, ok = 8, sin okm = 1/4.
Найти: S △omk — ?
Решение:
1) ( S = frac<1>2*a*b*sin α ) ( implies ) ( S = frac<1>2*mk*ok*sin okm )
2) S = 1/2 * 6 * 8 * 1/4 = 1/2 * 6 * 8 * 0.25 = 1/2 * 48 * 0.25 = 1/2 * 12 = 6
Ответ: Площадь треугольника omk равна 6.
Доказательство
Докажем, что площадь произвольного треугольника
равна полусумме произведения двух любых сторон
друг на друга, и на синус угла между этими сторонами.
Чтобы вам наглядно было видно, как мы доказываем,
используем один из известнейших треугольников — египетский треугольник.
Высота в египетском треугольнике равна длине одного из катетов.
Построим прямоугольный треугольник, изображенный на рисунке 2,
со сторонами 3,4,5 с одним из углов 90 градусов.
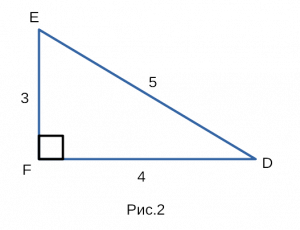
Первым делом найдем площадь обычной формулой,
затем с помощью синуса. Площадь равна половине
основания на высоту — ½3*4 = 6. Теперь найдем с
помощью синуса: ½3*4*sin90 = 6 * 1 = 6. Как видим,
полученные значения площадей сходятся, соответственно
через синус можно найти площадь треугольника ч.т.д.
Теперь, чтобы найти площадь треугольника нам не нужно
знать основание и высоту, можно знать только
две стороны и синус угла между ними.
Заключение
В заключение, можно сказать, что площадь
треугольника можно найти разными способами.
Например, в прямоугольном треугольнике площадь
рассчитать легче чем в любом другом треугольнике,
так как высота уже известна. Именно поэтому,
в школьном курсе, отчасти так подробно изучаются
прямоугольные треугольники. В Древнем Египте были
распространены прямоугольные треугольники со
сторонами 3,4,5; 6,8,10; 5,12,13. Длины этих прямоугольных
треугольников треугольников целые, что значительно,
упрощало разного рода вычисления.
Формулу площади треугольника делает универсальной то,
что она может применена к абсолютно любым треугольникам.
Главное, чтобы были известные две стороны,
и угол или синус угла между ними.
Формула площади треугольника через синус — универсальна,
поэтому может быть применена к любым видам треугольников.
[spoiler title=”источники:”]
http://mozgan.ru/Geometry/AreaTriangle
http://colibrus.ru/ploschad-treugolnika-cherez-sinus-ugla-i-dve-storony/
[/spoiler]
Площадь равнобедренного треугольника важна для вычисления многих геометрических и математических задач. Например, определение площади любого многоугольника связано с его разделением на ряд треугольников и расчетом площади каждого из них.
Геометрическое тело, обладающее двумя равными сторонами и углами – есть частный случай простого разностороннего многоугольника.
Каждая из идентичных линий называется боковой, а третья – основанием.

Если в таком треугольнике опустить среднюю линию из его вершины на 3-ю сторону, то образовавшиеся два плоских тела будут идентичны (так как имеют все признаки подобия).
Площадь (S) фигуры с тремя углами возможно установить:
-
по двум сторонам и высоте;
-
через угол между двумя сторонами и величину одной из них;
-
по двум сторонам;
-
через синус противолежащего основанию угла;
-
зная синус прилежащего угла и др.
Содержание
- Площадь равнобедренного треугольника через высоту
- Площадь равнобедренного треугольника через стороны
- Площадь равнобедренного треугольника через синус угла
- Формула площади равнобедренного треугольника через тангенс угла
Площадь равнобедренного треугольника через высоту
Вычисление площади треугольника с использованием его высоты и параметров основания – самый актуальный вариант, на базе которого строятся многие другие методы решения.
У планиметрической фигуры с двумя тождественными углами и боковыми отрезками высота может рассматриваться, как медиана и биссектриса. То есть линия, проведенная из вершины, делит планиметрический объект на два эквивалентных прямоугольных треугольника.
И общая их площадь сводится к:

где:
-
b — размер основания;
-
h – высота.
Задача №1.
Требуется рассчитать S тупоугольного равнобедренного многоугольника. Его h=3 см, а длина b = 8 см.
Вычисления выглядят следующим образом:

Ответ: 12 см2.
Площадь равнобедренного треугольника через стороны
Найти S планиметрического тела с двумя одинаковыми чертами, зная их параметры, возможно.
Для этого необходима теорема Пифагора, формулы которой видны на картинке,

и формула для отыскания S через биссектрису S = ½ * b * h.
После проведения медианы к середине 3-его отрезка, в равнобедренном треугольнике образуются 2 единообразных плоских тела с h между 2-мя катетами.
Таким образом, используя свойство сторон прямоугольного треугольника, выводим формулу, которая показана на картинке:

При высчитывание S равностороннего треугольника это выражение примет другой вид. Сравнить формулы нахождения площади равностороннего и равнобедренного треугольников можно, взглянув на картинку:

Задача №2.
У остроугольного равнобедренного треугольника даны габариты боковины b = 3 см и базиса a = 2 см. Надлежит найти его S:

Ответ: 8 см2.
Площадь равнобедренного треугольника через синус угла
В геометрии встречаются задания по отысканию площади многоугольника с тремя схожими краями через данный угол и длину прилегающей стороны.
В этой ситуации определение размера h будет осуществляться с использованием угла, прилегающего к измеренной грани. Таким образом выводится выражение, которое хорошо иллюстрирует следующая картинка:

Задача №3.
Посмотрим на рисунок, приведенный выше. Известно, что ∠ACB фигуры 30 градусов, а величина его боковой стороны AC = AB равняется 4 см. Требуется вычислить её S.

Ответ: 4 см2.
Формула площади равнобедренного треугольника через тангенс угла
Как правило, в планиметрии нередко встречаются задания по нахождению S треугольника, в котором определено значение стороны и угол.

Рисунок 1
Разнообразные равенства для решения задач, в том числе и нахождения S через тангенс угла, можно увидеть ниже:

Задача №4.
Дан равнобедренный треугольник OPQ (см. рис. 1). Известны величины: основание OQ = 5 см и угол QOP = 450. Требуется найти площадь треугольника OPQ.
Прежде всего посмотрим, как найти нам требуемую величину и какую применить формулу. Остановим свой выбор на формуле нахождения площади S по тангенсу угла.

Зная, что у нас равнобедренный треугольник, у которого углы у основания равны, найдем третий угол:
180 — 45 — 45 = 900 — угол OPQ.
Вычисляем SOPQ:
SOPQ = 52/4 * tg 45° = 25/4 * 1 = 6, 25 см2
Ответ: 6,25 см2.
Вот так, используя прежде всего знания о свойствах фигур, можно получать самые разнообразные способы вычисления той величины, какая требуется в задаче.
Предыдущая
ГеометрияПлощадь сферы – формулы и примеры вычислений
Следующая
ГеометрияТеорема о трех перпендикулярах – правило, формулировка и примеры решения задач

$$S = {bover 4}sqrt{4a^2-b^2}$$
Что обозначают буквы?
a – боковая сторона треугольника
b – основание треугольника

$$S = {1over 2}a^2sinalpha$$
Что обозначают буквы?
a – боковая сторона треугольника
α – угол между боковыми сторонами

$$S = {b^2over 4{tan{alpha over 2}}}$$
Что обозначают буквы?
b – основание треугольника
α – угол между боковыми сторонами

$$S = {1over 2}absinalpha$$
Что обозначают буквы?
a, b – стороны треугольника
α – угол между этими сторонами
Треугольник — многоугольник, образованный тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. При этом точки называются вершинами треугольника, а отрезки – его сторонами. Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла. Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Учебник
Геометрия, 9 класс
Формулы площадей через синус угла
Основные свойства площадей фигур:
- Равные фигуры имеют равные площади. Две фигуры состоящие из одинаковых кусков – равновеликие.
- Аддитивность: Площадь фигуры, разрезанной на несколько частей, равна сумме площадей этих частей ;
- Площадь прямоугольника равна произведению ширины на длину … произведение сторон.
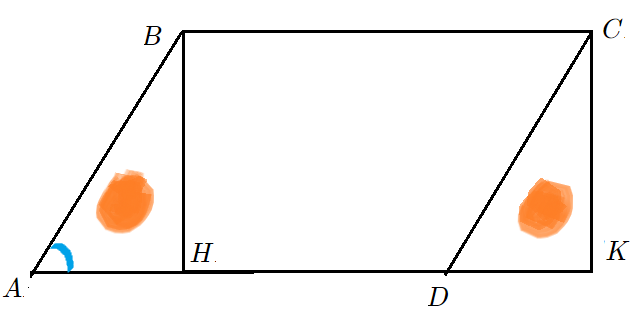
Задача 1: В параллелограмме известны стороны $7$, $10$ и синус угла между ними $frac{1}{2}$. Найти площадь параллелограмма.
- Решение: Опустим высоты $BH$ и $CK$ на основание $AD$ . Они помогут “увидеть” площадь.
- Что есть синус $angle BAH$ в прямоугольном треугольнике $bigtriangleup ABH$? Отношение катета $BH$ к гипотенузе $AB$.
- Формула синуса позволит выразить высоту $BH$ через сторону $AB$ и синус $frac{1}{2}$. Высота $CK$ такая же.
- Параллелограмм $ABCD$ состоит из кусков: $bigtriangleup ABH$ и $4$-угольник $HBCD$. Площадь – сумма площадей кусков.
- Прямоугольник $HBCK$ состоит из кусков $HBCD$ и $bigtriangleup DCK$. Площадь также “сумма кусков”.
- Треугольники $bigtriangleup ABH$ и $bigtriangleup DCK$ одинаковые. Значит, параллелограмм и прямоугольник равновеликие.
- Площадь Параллелограмма $ABCD$ так же, как прямоугольника $HBCD$ равна высота на основание.
- $S_{ABCD}=S_{ABH}+S_{HBCD}=S_{HBCD}+S_{DCK}=S_{HBCK}=BHcdot HK=ABcdotsin angle BADcdot AD=7cdotfrac{1}{2}cdot10$
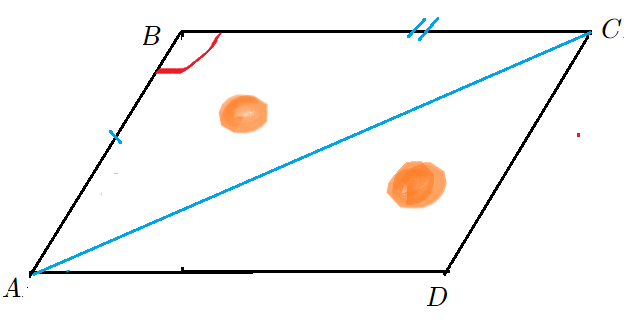
Теорема “о площади параллелограмма и треугольника через синус угла”:
- Площадь параллелограмма равна произведению сторон на синус угла параллелограмма:
- Формулы $S=acdot bcdotsin angle BAD$ $S_{ABCD}=ABcdot BCcdotsin D$
- Площадь треугольника равна половине произведения сторон треугольника на синус угла между ними.
- Формулы $S=frac{1}{2}cdot acdot bcdotsin angle C$ $S_{bigtriangleup ABC}=frac{1}{2}cdot ABcdot BCcdotsin angle CBA$
Площадь треугольника также легко получить через площадь параллелограмма, равновеликого с двумя треугольниками, приставленными друг к другу по диагонали. Тогда площадь одного треугольника будет равна половине площади параллелограмма с тем же основанием и с той же высотой.
Задача 2: Диагонали четырехугольника делятся точкой пересечения на отрезки $3$, $5$ и $6$, $7$ . Синус угла между диагоналями $0,2$. Найти площади треугольников и всего четырехугольника.
- Дано: $BO=3$ $OD=5$ $CO=6$ $AO=7$ … угол между $sinangle AOB=0,2$. Найти: $S_{ABCD}=?$.
- Решение: Диагонали делят четырехугольник на 4 треугольника. Площадь = сумме 4-х площадей.
- Аддитивность: $S_{ABCD}=S_{bigtriangleup AOB}+S_{bigtriangleup BOC}+S_{bigtriangleup COD}+S_{bigtriangleup AOD}$.
- Площадь одного из них по формуле: $S_{bigtriangleup AOB}=frac{1}{2}cdot AOcdot OBcdot sin angle AOB=frac{1}{2}cdot 7 cdot 3cdot 0,2=2,1$
- Каковы синусы остальных углов? Свойство: Синусы смежных углов равны: $sinangle BOC=sinangle COD=sinangle AOD=0,2$
- Тогда, площади других треугольников $frac{1}{2}cdot 3 cdot 6cdot 0,2=1,8$ $frac{1}{2}cdot 6 cdot 5cdot 0,2=3$ $frac{1}{2}cdot 5 cdot 7cdot 0,2=3,5$
- Площадь четырехугольника равна сумме этих площадей Ответ: $S_{ABCD}=2,1+1,8+3+3,5=10,4$
Теоретически, по-другому: Распишем получение площади $S_{ABCD}$ в буквах, без числовых значений:
- $frac{1}{2}cdot OAcdot OBcdot sin angle AOB+frac{1}{2}cdot OBcdot OCcdot sin angle AOB+frac{1}{2}cdot OCcdot ODcdot sin angle AOB+frac{1}{2}cdot ODcdot OAcdot sin angle AOB$
- Вынос за скобки множителей $S_{ABCD}=frac{1}{2}cdot sin angle AOBcdot left(OAcdot OB+OBcdot OC+OCcdot OD+ODcdot OAright)$
- $S_{ABCD}=frac{1}{2}cdot sin angle AOBcdot left(OBcdotleft(OA+OCright)+ODcdotleft(OA+OCright)right)=frac{1}{2}cdot sin angle AOBcdot AC cdot (OB+OD)$
- Получаем $S_{ABCD}=frac{1}{2}cdot AC cdot BDcdot sin angle AOB$ $Rightarrow$ $S_{ABCD}=frac{1}{2}cdot (7+6) cdot (3+5)cdot 0,2=13cdot 0,8=10,4$

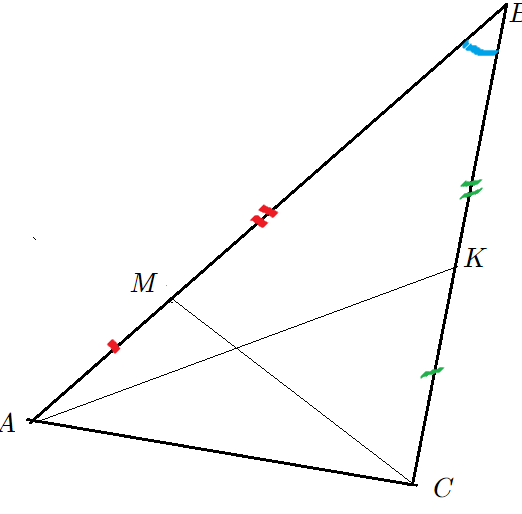
Задача 3: В треугольнике известны стороны $AB=10$ , $BC=12$ и угол $angle ABC=30$ . Точка $M$ делит сторону $AB$ в отношении 3 : 5, а точка $K$ делит сторону $BC$ в отношении 2 : 3. Найти площади и отношение площадей треугольников $ABK$ и $MBC$.
- Дано: $AB=10$, $BC=12$, $frac{AM}{MB}=frac{3}{5}$, $frac{BK}{KC}=frac{2}{3}$, $angle ABC=30$. Найти: $frac{S_{bigtriangleup ABK}}{S_{bigtriangleup MBC}}=?$
- Точка делит отрезок в известном соотношении. Находим части как систему уравнений $frac{x}{y}=?$ $x+y=?$
- $frac{AM}{MB}=frac{3}{5}$, аддитивность $AM+MB=AB=10$ $Rightarrow$ $frac{AM}{AB}=frac{3}{3+5}$ $Rightarrow$ $AM=frac{15}{4}$, $MB=frac{25}{4}$
- $frac{BK}{KC}=frac{2}{3}$, $BK+KC=12$ из свойств пропорций $BK=frac{24}{5}$, $KC=frac{36}{5}$
- Найдем площадь через синус $S_{bigtriangleup ABK}=frac{1}{2}cdot AB cdot BK cdot sin angle ABC = frac{1}{2}cdot 10 cdot frac{24}{5} cdot sin 30= 24 cdot 0,5=12$
- В треугольнике $MBC$ тот же угол, $S_{bigtriangleup MBC}=frac{1}{2}cdot MB cdot BC cdot sin angle ABC = frac{1}{2}cdot frac{25}{4} cdot 12 cdot 0,5=frac{75}{4}$
- отношение площадей треугольников $frac{S_{bigtriangleup ABK}}{S_{bigtriangleup MBC}}=frac{12}{frac{75}{4}}=frac{16}{25}$ Ответ: $frac{16}{25}$
Замечание, продолжение: Можно ли найти отношение площадей при неизвестных значениях сторон и угла?
- Зная лишь как делят точки $M$ и $K$ стороны треугольника, на какие пропорции ?!
- Дано только $frac{AM}{MB}=frac{3}{5}$, $frac{BK}{KC}=frac{2}{3}$. Выразим отрезки через стороны $AB$ и $BC$.
- Выразим площади $S_{bigtriangleup ABK}$ , $S_{bigtriangleup MBC}$ также через стороны $AB$ и $BC$ и угол $angle ABC$.
- Составим отношение площадей, выразим через стороны и угол. Что получится? Что можно сделать, ?
Теорема “о площади четырехугольника через диагонали и синус угла”:
- Площадь четырехугольника равна половине произведения диагоналей на синус угла между ними:
- Формулы $S=frac{1}{2}cdot d_1 cdot d_2 cdotsin angle alpha$ $S_{ABCD}=frac{1}{2}cdot AC cdot BDcdot sin angle AOB$
- Площадь ромба равна половине произведения диагоналей. … диагонали перпендикулярны!
- Формулы $S=frac{1}{2}cdot d_1 cdot d_2=frac{1}{2}cdot AC cdot BD$ $angle AOB=90$ $sin angle AOB=1$
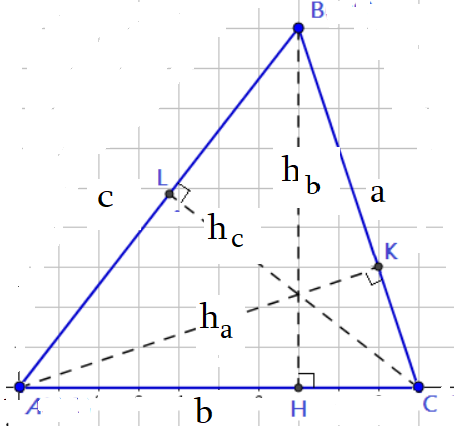
Формулы площади треугольника:
$S=frac{acdot h_a}{2}=frac{acdot bcdotsin C}{2}$ $S=frac{bcdot h_b}{2}=frac{bcdot ccdotsin A}{2}$ $S=frac{ccdot h_c}{2}=frac{ccdot acdotsin B}{2}$.
$sin A=frac{h_b}{c}=frac{h_c}{b}$ $sin B=frac{h_a}{c}=frac{h_c}{a}$ $sin C=frac{h_b}{a}=frac{h_a}{b}$.
$S_{ABC}=frac{1}{2}cdot ACcdot BCcdotsin C$ $S_{ABC}=frac{1}{2}cdot ABcdot BCcdotsin B$ $S_{ABC}=frac{1}{2}cdot ACcdot ABcdotsin A$ .
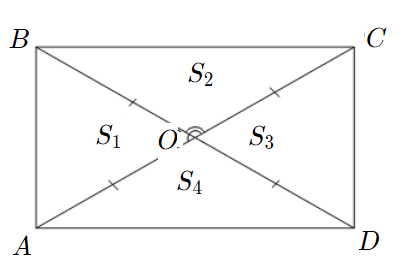
Задача 4: В прямоугольнике диагонали $10$ и угол между ними $30$. Найти площадь.
- Дано: $ABCD$ – прямоугольник , $AC=10$ , $angle AOB=30$ Найти: $S_{ABCD}$ .
- Решение: В прямоугольнике диагонали равны и пересекаются по середине $AO=OB=5$
- $bigtriangleup AOB$ и $bigtriangleup COD$ равные $Rightarrow$ $S_1=S_3$ ;
- $bigtriangleup BOC$ и $bigtriangleup AOD$ равные $Rightarrow$ $S_2=S_4$ .
- Смежные, $angle BOC=180-angle AOB=150$. Найдем отношение $frac{S_1}{S_2}=frac{frac{1}{2}AOcdot OBcdotsin30}{frac{1}{2}BOcdot OCcdotsin150}$
- $sin30=sinleft(180-30right)=sin150$. тогда $frac{S_1}{S_2}=frac{frac{1}{2}cdot5cdot5cdotsin150}{frac{1}{2}cdot5cdot5cdotsin150}=1$ Значит, $S_1=S_2$
- Аналогично: $frac{S_3}{S_4}=frac{frac{1}{2}DOcdot OCcdotsin30}{frac{1}{2}AOcdot ODcdotsin150} =1$ $Rightarrow$ $S_3=S_4$, площади равные.
- Диагонали рассекают прямоугольник на четыре равновеликих: треугольника $S_1=S_2=S_3=S_4$ .
- … тогда, по свойству аддитивности площадей $S_1=S_2=S_3=S_4=frac{1}{4}S_{ABCD}$ .
- $S_{AOB}=S_1=frac{1}{2}AOcdot OBcdot sin 30=frac{1}{2}cdot 5cdot 5cdot frac{1}{2}=frac{25}{4}$ $Rightarrow$ $S_{ABCD}=4cdotfrac{25}{4}$
- Найдя площадь АОВ, нашли площадь прямоугольника умножением на 4. Ответ: $S_{ABCD}=25$
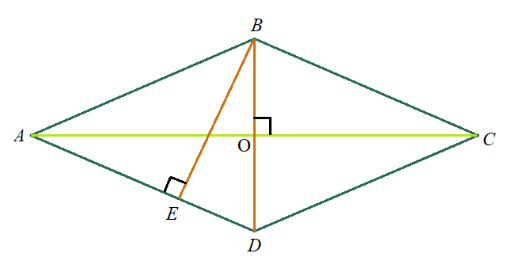
Задача 5: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Дано: ромб $ABCD$ , $BD=13$, высота $EB=12$ , Найти: $S_{ABCD}$ .
- Решение: прямоугольный $bigtriangleup BED$, подобен тем, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Одинаковый “состав” углов. Все прямоугольные,
- Прямоугольный $bigtriangleup BED$, по Пифагору выразим катет $DE=sqrt{BD^2-BE^2}=5$
- Диагонали в ромбе делятся пополам: $BO=OD=frac{BD}{2}=6,5$ $AO=frac{AC}{2}$ $AC=2cdot AO$
- Для нахождения площади ромба нам нужно найти вторую диагональ.
- $bigtriangleup BED sim bigtriangleup AOD$ $Rightarrow$ $frac{AO}{BE}=frac{OD}{ED}$ $Rightarrow$ $AO=frac{ODcdot BE}{ED}=frac{6,5cdot 12}{5}=15,6$ $AC=2cdot AO=31,2$
- Ответ: Площадь ромба через диагонали: $S_{ABCD}=frac{1}{2}cdot ACcdot BD=0,5cdot 31,2cdot13=202,8$


Задача 6. Площадь равнобедренного треугольника равна $100$ , а угол при вершине $30^o$ 1) Найти его боковые стороны . 2) Найти тригонометрию $15^o$
- Решение: 1) Известны площадь и угол, значит используем формулу площади через синус $30^o$ .
- Пусть боковая сторона $a$ , $S=frac{1}{2}acdot acdotsin30$ , тогда $100=frac{1}{2}a^2cdotsin30$ $Leftrightarrow$ $100=frac{1}{2}a^2cdotfrac{1}{2}$ $Rightarrow$
- $a=sqrt{400}=20$ Ответ: $a=20$
- 2) По теореме косинусов найдем основание $c=sqrt{a^2+a^2-2cdot acdot acdotfrac{sqrt{3}}{2}}=asqrt{2-sqrt{3}}$
- Из вершины равнобедренного угла проведем биссектрису к основанию. По свойству равнобедренности
- она будет и высотой $h$ (треугольник поделится на 2 прямоугольных с углами 15 градусов) и медианой,
- а значит основание поделится пополам , как и угол 30 у вершины поделится по 15 градусов.
- По прямоугольнему треугольнику (половинка): $sin15=frac{0,5cdot c}{a}=frac{0,5cdot acdotsqrt{2-sqrt{3}}}{a}=frac{sqrt{2-sqrt{3}}}{2}$
- Площадь через основание $S=frac{1}{2}cdot ccdot h$, найдем высоту $h=frac{2cdot S}{c}=frac{2cdot0,5cdot a^2cdotsin30}{acdotsqrt{2-sqrt{3}}}=frac{a}{2cdotsqrt{2-sqrt{3}}}$
- В прямоугольном треугольнике стороны $h$, $frac{c}{2}$, $a$. Тогда $cos15=frac{h}{a}=frac{frac{a}{2cdotsqrt{2-sqrt{3}}}}{a}=frac{1}{2cdotsqrt{2-sqrt{3}}}$