You should upgrade or use an alternative browser.
-
Forums
-
Homework Help
-
Introductory Physics Homework Help
Density of a Spring
-
Thread starter
mkarydas -
Start date
Mar 12, 2014
- Mar 12, 2014
- #1
A spring has one side attached to the wall and the other one free.The spring has at rest
length L, and linear mass density ρ(x)= constant. Suppose we pull the spring to a new length L’.
1)Find the new mass density of the spring ρ'(x).
Now after trying it at home with a spring it is clear to me that the mass density of the spring becomes smaller as we get from the wall to the other end (after i have streched it). So there must be an explanation to this…
Answers and Replies
- Mar 12, 2014
- #2
One side gets shorter, the other gets longer. The effects cancel, the volume remains the same, as does the density.
- Mar 12, 2014
- #3
Now after trying it at home with a spring it is clear to me that the mass density of the spring becomes smaller as we get from the wall to the other end (after i have streched it). So there must be an explanation to this…
… how did you determine the mass density so that it was clear to you?
This is a startling result, please be specific about the kind of spring and what measurements you made.
Be careful to define your terms.
Note: the spring constant depends on the density of the material – if density changed so easily, then the spring constant would not be, um, constant…
- Mar 12, 2014
- #4
Chet
- Mar 12, 2014
- #5
- Mar 12, 2014
- #6
This is not the kind of thing that a student is likely to notice in an improvised experiment at home.
We can also imagine the spring is not made of coils – we just have a straight length of metal, fix one end, pull (very hard) on the other end – the metal gets longer and the sides “suck in” … mass stays the same so the linear mass density is lower.
Maybe it is a torsional spring, or a bent-beam spring?
Of course we could use a rubber band – but is that a good “spring” for these purposes: the slightest pull may pass it’s elastic limit?
All this is why I want to see the details of the experiment before commenting properly.
- Mar 13, 2014
- #7
- Mar 13, 2014
-
- #8
The linear mass density of the spring is the number of coils per unit length.
Now if you stretch the spring then the number of coils per Δχ is not the same everywhere in the spring. (There are more coils per unit length at the wall than at the other end which means the linear density drops)
In other words the spring appears more stretched at the other end than at the end attached to the wall.
I have included a picture which shows that a stretched spring has the same number of coils per length everywhere (maybe this is idealized but still has to be explained theoretically) but this is NOT what you see if you do the experiment at home with a normal spring.
Attachments
-
250px-HookesLawForSpring-English.png
- Mar 13, 2014
- #9
I have included a picture which shows that a stretched spring has the same number of coils per length everywhere (maybe this is idealized but still has to be explained theoretically) but this is NOT what you see if you do the experiment at home with a normal spring.
It’s fairly easy to calculate the number of coils per unit length at each point along the spring’s length as a function of the spring’s stiffness at each point. If the spring has the same stiffness all along its length, the coils will be evenly spaced. If it doesn’t, they won’t be.
I conclude that your spring is not uniform along its length.
- Mar 13, 2014
- #10
Suppose you take a steel spring of given length and number of coils/unit length.
The linear mass density of the spring is the number of coils per unit length.
Now if you stretch the spring then the number of coils per Δχ is not the same everywhere in the spring. (There are more coils per unit length at the wall than at the other end which means the linear density drops)
In other words the spring appears more stretched at the other end than at the end attached to the wall.
I have included a picture which shows that a stretched spring has the same number of coils per length everywhere (maybe this is idealized but still has to be explained theoretically) but this is NOT what you see if you do the experiment at home with a normal spring.
Flip your spring around and do the experiment again. Is the spring density now higher away from the wall?
- Mar 13, 2014
- #11
The spring has the same density when it is not stretched and it doesn’t matter which side i stick to the wall..
- Mar 13, 2014
- #12
- Mar 13, 2014
-
- #13
it is clear to me that the mass density of the spring becomes smaller as we get from the wall to the other end (after i have streched it).
Please explain why “it is clear to you”.
The simplest explanation for all this is “you believe something which is not true”, but unless you tell us WHY you think it is true, we can’t explain why you are wrong.
- Mar 13, 2014
- #14
- Mar 13, 2014
- #15
Is the spring vertical, by any chance?
Y’know, I had been wondering the same thing
although the original attachment shows the springs drawn horizontally…
- Mar 13, 2014
- #16
What dauto said how does the spring know the difference between a still hand and the wall is true, meaning it shouldn’t know… Although if you do the experiment for example with a rubber band of a given color ( blue) then the side near to the wall is darker than the side of your hand ( because it is more dense) …
- Mar 13, 2014
- #17
A horizontal real spring is (usually) supported by a surface which will add drag when the spring is extended slightly. This can produce a varied coil density with horizontal distance. Perhaps in the home experiment
mkarydas had the spring lying on the ground or a table-top?
If it is supported only at the ends, then the spring will form a catenary – will will also show a changing coil density with horizontal length.
If the spring is suspended vertically, then the total mass below the higher spring elements is greater – resulting in a greater extension the farther up you go. (I’m looking for an unambiguous picture of this online btw.)
But if we define mass-per-unit-length in terms of the path around the coils, that is a different story.
It seems that this was not what OP intended by linear mass density. <phew>.
Breaking the spring into small elements should be able to deal with the case that there are no drag or weight forces acting on it – but this is not a situation you can easily test at home.
- Mar 14, 2014
- #18
If the spring is suspended vertically, then the total mass below the higher spring elements is greater – resulting in a greater extension the farther up you go. (I’m looking for an unambiguous picture of this online btw.)
https://www.youtube.com/watch?v=SArLksloZ9E
Just the first few seconds. Apart from the fact that they have a computer simulation of something, I’ve no idea what the rest of the video is about.
This effect doesn’t show up for most real springs, because the tension required to stretch them significantly is much greater than their weight.
- Mar 14, 2014
- #19
This effect doesn’t show up for most real springs, because the tension required to stretch them significantly is much greater than their weight.
There are quite stretchy plastic slinkies though – the pics I’ve found showing the effect all leave off the support or they are computer simulations of a spring.
There are videos of suspended slinkies getting released:
i.e.
The first one is quite clear… I could take a still from that.
Suggested for: Density of a Spring
- May 1, 2023
- Feb 7, 2023
- Jan 27, 2023
- Dec 4, 2022
- Feb 8, 2023
- Oct 21, 2022
- Sep 22, 2022
- Feb 17, 2023
- Feb 20, 2023
- Feb 13, 2023
-
Forums
-
Homework Help
-
Introductory Physics Homework Help
Вопрос сколько весит пружина носит важный практический характер.
Если нет весов, то как эту массу пружины рассчитать?
Нужно перемножить объем пружины на её плотность.
Объем пружины зависит от диаметра и количества витков.
Плотность от типа материала.
Калькулятор расчета массы пружины здесь.
Как всегда всё просто! Вес пружины это результат перемножения её объема на плотность.

ПОМОГИТЕ С ФИЗИКОЙ СРОЧНО!!
1) Определить коэффициент жесткости пружины с помощью динамометра и груза, массой 100 гр.
2)как определить плотность твердого тела с помощью линейки и весов.
3) определить фокус тонкой линзы
Светило науки – 2 ответа – 0 раз оказано помощи
1. Сила которая будет на динамометре разделить на величину равную разности длины пружины с подвешенным грузом и без него.
2. С помощью линейки измерить высоту длину и ширину тела и перемножить эти величины – получишь объем тела, взвесить на весах тело – получишь массу тела, плотность равна отношению массы и объема, p=m/V
Основные
понятия
Пружина
растяжения — это спирально-цилиндрическая
пружина, витки которой прилегают друг
к другу. Пружина подвергается действию
противоположно направленных усилий,
приложенных вдоль ее оси.
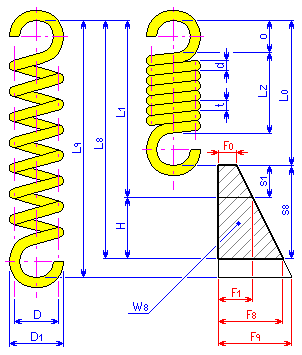
Размеры
|
d |
диаметр |
|
D |
средний |
|
D1 |
наружный |
|
D2 |
внутренний |
|
H |
рабочая |
|
t |
шаг |
|
o |
высота |
|
sx |
деформация |
|
Lx |
длина |
|
Fx |
рабочая |
|
W8 |
энергия |
|
x |
индекс, |
Навивка
-
Вправо
(стандарт) -
Влево
(должна отображаться соответствующая
надпись)
Состояния
-
Свободное:
пружина не нагружена (индекс 0) -
Предварительная
нагрузка: пружина с минимальной рабочей
нагрузкой (индекс 1) -
Полная
нагрузка: пружина с максимальной рабочей
нагрузкой (индекс 8) -
Предел:
пружина вдавлена до касания витков
(индекс 9).
Зацепы
пружин растяжения
Высота
зацепа пружины растяжения
Где:
|
L0 |
длина |
|
LZ |
длина |
Часто
используемые зацепы пружин растяжения
|
Тип |
Изображение |
|
Половина |
|
|
Обычно |
|
|
Полный |
|
|
Используется |
|
|
Полный |
|
|
Когда |
|
|
Полный |
|
|
Обычно |
|
|
Поднятый |
|
|
Обычно |
|
|
Два |
|
|
Используется |
|
|
Два |
|
|
Когда |
Расчет
пружин в метрических единицах
Общие
формулы расчета
Коэффициент
использования материала
Наружный
диаметр пружины
D1 =
D + d [мм]
Где:
|
D |
средний |
|
|
d |
диаметр |
Внутренний
диаметр пружины
D2 =
D – d [мм]
Где:
|
D |
средний |
|
|
d |
диаметр |
Рабочая
деформация
H
= L81=
s81[мм]
Где:
|
L8 |
длина |
|
|
L1 |
длина |
|
|
s8 |
деформация |
|
|
s1 |
деформация |
Высота
зацепа пружины
Где:
|
L0 |
длина |
|
|
LZ |
длина |
Индекс
пружины
c
= D/d [-]
Где:
|
D |
средний |
|
|
d |
диаметр |
Поправочный
коэффициент Валя
Где:
|
c |
индекс |
|
|
LZ |
длина |
Начальное
растяжение
Где:
|
d |
диаметр |
|
|
0 |
напряжение |
|
|
D |
средний |
|
|
Kw |
поправочный |
Общая
сила, действующая в пружине
Где:
|
d |
диаметр |
|
|
G |
напряжение |
|
|
D |
средний |
|
|
Kw |
поправочный |
|
|
G |
модуль |
Жесткость
пружины
Где:
|
d |
диаметр |
|
|
G |
модуль |
|
|
D |
средний |
|
|
n |
количество |
|
|
F8 |
рабочее |
|
|
F1 |
рабочее |
|
|
H |
рабочая |
Расчет
конструкции пружины
При
проектировании пружины подбирается
диаметр проволоки, количество витков
и длина свободной пружины L0 для
заданной нагрузки, материала и сборочных
размеров.
Если
рассчитанная пружина не соответствует
ни одному значению диаметра проволоки
для данного напряжения 0 согласно
формуле, расчет пружины повторяется с
использованием скорректированного
значения напряжения в свободном состоянии
из рекомендуемого диапазона.
Пружине
без начального растяжения соответствует
средний рекомендуемый шаг витков t =
0,35 D [мм].
Если
рассчитанная пружина не соответствует
ни одному значению диаметра проволоки
для выбранного шага, расчет пружины
повторяется с использованием
скорректированного значения шага из
рекомендуемого диапазона 0,3 D ≤ t ≤ 0,4
D [мм].
Конструкция
пружины определяется с учетом условия
прочности 8≤ usA и
рекомендуемых диапазонов некоторых
геометрических параметров пружины:
L0≤ D
и L0≤ 31,5
д и 4 ≤ D/d ≤16 и n 2.
Задание
нагрузки, материала и сборочных размеров
пружины
Вначале
выполняется проверка входных величин
для расчета.
Затем
вычисляется длина пружины в свободном
состоянии.
После
расчета выбирается диаметр проволоки,
количество витков и диаметры пружины
– так, чтобы высота зацепа соответствовала
выбранному типу зацепа. Кроме того,
должны выполняться упомянутые выше
прочностные и геометрические условия.
Конструкция пружины должна удовлетворять
по диаметрам всем заданным начальным
условиям. При отсутствии таких
дополнительных условий предельный
диаметр пружины устанавливается по
геометрическим условиям для
минимально/максимально допустимого
диаметра проволоки.
Отбираются
все диаметры проволоки (от меньшего к
большему), которые проходят по прочностным
и геометрическим условиям. Проверяются
высота зацепа и количество витков. Если
все условия выполнены, расчет конструкции
завершается, и текущие значения параметров
принимаются в качестве его результатов,
независимо от того, как прошел бы расчет
при других подходящих диаметрах
проволоки. Таким образом, полученная
пружина имеет минимально возможный
диаметр проволоки и минимально возможное
количество витков.
Вычисленное
значение высоты зацепа должно находиться
в пределах d ≤ o ≤ 30 d. Комбинация
диаметра проволоки, количества витков
и диаметра пружины должна давать в итоге
такую высоту зацепа, которая удовлетворяет
его типу. Вначале в качестве типа зацепа
берется полный виток, затем, если он не
годится–полный виток внутри и т.д.
Задание
нагрузки, материала и диаметра пружины
Вначале
выполняется проверка входных величин
для расчета.
После
проверки выбирается диаметр проволоки,
количество витков, длина пружины в
свободном состоянии и сборочные размеры
пружины – так, чтобы высота зацепа
соответствовала выбранному типу зацепа.
Кроме того, должны выполняться прочностные
и геометрические условия. Если сборочный
размер L1 или
L8 взят
из спецификации или значение рабочей
деформации пружины ограничено, конструкция
пружины должна соответствовать этому
условию. В остальных случаях предельные
значения сборочных размеров пружины и
ее длины в свободном состоянии определяются
геометрическими условиями для заданного
диаметра пружины и минимального/максимального
допустимого диаметра проволоки.
Формула
для проектирования пружины по заданному
диаметру проволоки.
где
значение 8 =
0,85 A используется
в качестве величины напряжения материала
пружины при кручении в полностью
нагруженном состоянии.
Если
для данного диаметра проволоки не
удается подобрать подходящую комбинацию
размеров пружины, расчетная процедура
оценивает другие диаметры проволоки.
Они проверяются, начиная от меньшего к
большему, до тех пор пока не будет
достигнуто такое количество витков,
при котором высота зацепа удовлетворяет
всем условиям. Расчет конструкции
завершается, и текущие значения параметров
принимаются в качестве его результатов,
независимо от того, как прошел бы расчет
при других подходящих диаметрах
проволоки. Таким образом, полученная
пружина имеет минимально возможный
диаметр проволоки и минимально возможное
количество витков.
Вычисленное
значение высоты зацепа должно находиться
в пределах d ≤ o ≤ 30 d. Для
высоты, вычисленной таким способом,
выбирается соответствующий тип зацепа.
Комбинация диаметра проволоки, количества
витков, длины пружины в свободном
состоянии и сборочных размеров пружины
должна давать в итоге такую высоту
зацепа, которая удовлетворяет его типу.
Вначале в качестве типа зацепа берется
полный виток, затем, если он не
годится–полный виток внутри и т.д.
Задание
максимального рабочего усилия, материала,
сборочных размеров и диаметра пружины
Вначале
выполняется проверка входных величин
для расчета.
Затем
подбирается диаметр проволоки, количество
витков, длина свободной пружины и
минимальное рабочее усилие F1 таким
образом, чтобы высота зацепа пружины
соответствовала выбранному типу зацепа.
Кроме того, должны выполняться прочностные
и геометрические условия.
Формула
для проектирования пружины по заданному
диаметру проволоки.
где
значение 8 =
0,9 A используется
в качестве величины напряжения материала
пружины при кручении в полностью
нагруженном состоянии.
Если
для данного диаметра проволоки не
удается подобрать подходящую комбинацию
размеров пружины, расчетная процедура
оценивает другие диаметры проволоки.
Они проверяются, начиная от меньшего к
большему, до тех пор пока не будет
достигнуто такое количество витков,
при котором высота зацепа удовлетворяет
всем условиям. Расчет конструкции
завершается, и текущие значения параметров
принимаются в качестве его результатов,
независимо от того, как прошел бы расчет
при других подходящих диаметрах
проволоки. Таким образом, полученная
пружина имеет минимально возможный
диаметр проволоки и минимально возможное
количество витков.
Проверочный
расчет пружины
Расчет
соответствующих значений сборочных
размеров и рабочего отклонения для
указанной нагрузки, материала и размеров
пружины.
Сначала
проверяются расчетные входные значения.
Затем на основании приведенных ниже
формул вычисляются сборочные размеры.
Длина
предварительно нагруженной пружины
Длина
полностью нагруженной пружины
Где:
|
L0 |
длина |
|
|
F1 |
рабочая |
|
|
D |
средний |
|
|
n |
количество |
|
|
G |
модуль |
|
|
d |
диаметр |
|
|
F8 |
рабочее |
Рабочая
деформация
H
= L18[мм]
Расчет
рабочих сил
Расчет
соответствующих сил, действующих в
пружинах в рабочем состоянии для
указанного материала, сборочных размеров
и размеров пружины. Сначала проверяются
и рассчитываются входные данные, а затем
выполняется расчет рабочих сил с помощью
следующих формул.
Минимальное
рабочее усилие
Максимальное
рабочее усилие
Расчет
выходных параметров пружины
Эта
часть является общей для всех типов
расчета пружины. Расчет производится
в следующем порядке.
Коэффициент
высоты зацепа
Жесткость
пружины
Длина
части с витками
|
Пружина |
|
|
Lz = |
|
|
Пружина |
|
|
Lz = |
Деформация
предварительно нагруженной пружины
s1 =
L1 –
L0 [мм]
Полная
деформация пружины
s8 =
L8 –
L0 [мм]
Напряжение
при кручении материала пружины в
состоянии предварительной нагрузки
Напряжение
материала пружины при кручении при
полном нагружении
Предельное
усилие в пружине
Деформация
в предельном состоянии
Где:
|
k |
жесткость |
|
|
F9 |
рабочее |
|
|
F0 |
начальное |
Предельная
длина пружины
L9 =
L0 +
s9 [мм]
Энергия
деформации пружины
Длина
развернутой проволоки
|
l |
|||
|
Где |
|||
|
для |
|||
|
l0 = D |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = D |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = |
Масса
пружины
Собственная
частота колебаний пружины
Проверка
нагрузки пружины
8≤ us
A
Обзор
используемых переменных:
|
d |
диаметр |
|
k |
жесткость |
|
D |
средний |
|
D1 |
наружный |
|
D2 |
внутренний |
|
F |
обобщенное |
|
G |
модуль |
|
H |
рабочая |
|
c |
индекс |
|
Kw |
поправочный |
|
l |
длина |
|
L |
обобщенная |
|
LZ |
длина |
|
m |
масса |
|
n |
количество |
|
o |
высота |
|
t |
шаг |
|
s |
обобщенная |
|
us |
коэффициент |
|
|
плотность |
|
|
напряжение |
|
A |
допустимое |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины. Что же это за величина, и как она связана с деформацией тел и законом Гука?
Содержание:
- Сила упругости и закон Гука
- Определение коэффициента жесткости
- Расчет жесткости системы
- Последовательное соединение системы пружин
- Параллельное соединение системы пружин
- Вычисление коэффициента жесткости опытным методом
- Примеры задач на нахождение жесткости
- Видео
Сила упругости и закон Гука
Для начала определим основные термины, которые будут использоваться в данной статье. Известно, если воздействовать на тело извне, оно либо приобретет ускорение, либо деформируется. Деформация — это изменение размеров или формы тела под влиянием внешних сил. Если объект полностью восстанавливается после прекращения нагрузки, то такая деформация считается упругой; если же тело остается в измененном состоянии (например, согнутом, растянутом, сжатым и т. д. ), то деформация пластическая.
Примерами пластических деформаций являются:
- лепка из глины;
- погнутая алюминиевая ложка.
В свою очередь, упругими деформациями будут считаться:
- резинка (можно растянуть ее, после чего она вернется в исходное состояние);
- пружина (после сжатия снова распрямляется).
В результате упругой деформации тела (в частности, пружины) в нем возникает сила упругости, равная по модулю приложенной силе, но направленная в противоположную сторону. Сила упругости для пружины будет пропорциональна ее удлинению. Математически это можно записать таким образом:
F = – k·x;
где F — сила упругости, x — расстояние, на которое изменилась длина тела в результате растяжения, k — необходимый для нас коэффициент жесткости. Указанная выше формула также является частным случаем закона Гука для тонкого растяжимого стержня. В общей форме этот закон формулируется так: «Деформация, возникшая в упругом теле, будет пропорциональна силе, которая приложена к данному телу». Он справедлив только в тех случаях, когда речь идет о малых деформациях (растяжение или сжатие намного меньше длины исходного тела).
Определение коэффициента жесткости
Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:
k = F/x.
Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.
Единица измерения жесткости в СИ — Н/м.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.
Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
k = k1 + k2 + … + ki.
Измерение жесткости пружины опытным путем – в этом видео.
Вычисление коэффициента жесткости опытным методом
С помощью несложного опыта можно самостоятельно рассчитать, чему будет равен коэффициент Гука. Для проведения эксперимента понадобятся:
- линейка;
- пружина;
- груз с известной массой.
Последовательность действий для опыта такова:
- Необходимо закрепить пружину вертикально, подвесив ее к любой удобной опоре. Нижний край должен остаться свободным.
- При помощи линейки измеряется ее длина и записывается как величина x1.
- На свободный конец нужно подвесить груз с известной массой m.
- Длина пружины измеряется в нагруженном состоянии. Обозначается величиной x2.
- Подсчитывается абсолютное удлинение: x = x2-x1. Для того чтобы получить результат в международной системе единиц, лучше сразу перевести его из сантиметров или миллиметров в метры.
- Сила, которая вызвала деформацию, — это сила тяжести тела. Формула для ее расчета — F = mg, где m — это масса используемого в эксперименте груза (переводится в кг), а g — величина свободного ускорения, равная приблизительно 9,8.
- После проведенных расчетов остается найти только сам коэффициент жесткости, формула которого была указана выше: k = F/x.
Примеры задач на нахождение жесткости
Задача 1
На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.
- Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
- По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.
Ответ: жесткость пружины составит 2500 Н/м.
Задача 2
Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.
- Найдем силу тяжести, деформирующей пружину: F = mg = 10 · 9.8 = 98 Н.
- Определим коэффициент упругости: k = F/x = 98 / 0.04 = 2450 Н/м.
- Рассчитаем, с какой силой действует второй груз: F = mg = 25 · 9.8 = 245 Н.
- По закону Гука запишем формулу для абсолютного удлинения: x = F/k.
- Для второго случая подсчитаем длину растяжения: x = 245 / 2450 = 0,1 м.
Ответ: во втором случае пружина растянется на 10 см.
Видео
Из этого видео вы узнаете, как определить жесткость пружины.