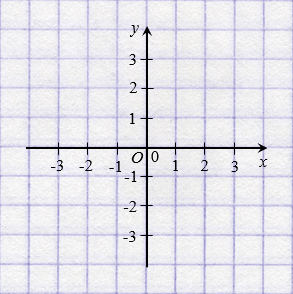Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Как найти координаты точки
Поддержать сайт
Каждой точке координатной плоскости соответствуют две координаты.
Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.
Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.
Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».
Обозначают координаты точки, как указано выше (·) A (2; 3).
Пример (·) A (2; 3) и (·) B (3; 2).
Запомните!
На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.
Особые случаи расположения точек
- Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0). - Начало координат — точка O имеет координаты, равные нулю O (0,0).
- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).
Как найти положение точки по её координатам
Найти точку в системе координат можно двумя способами.
Первый способ
Чтобы определить положение точки по её координатам,
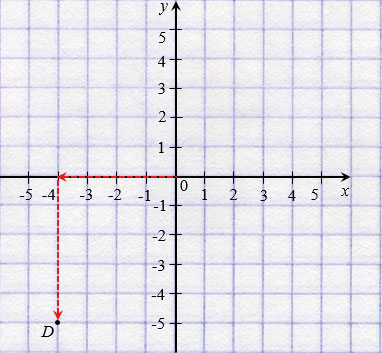
например, точки D (−4 , 2), надо:
- Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox». - Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy». - Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.
Второй способ
Чтобы найти точку D (−4 , 2) надо:
- Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−». - Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».
Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Координаты на плоскости
- Координатная плоскость
Указать положение точки на плоскости можно с помощью координат. Для этого проведем на плоскости две перпендикулярные координатные прямые так, чтобы их начала отсчета совпадали.
Эти прямые называют осями координат, точку их пересечения О – начало отсчета.
Горизонтальная ось – ось абсцисс, обозначают буквой 

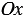
Вертикальная ось – ось ординат, обозначают буквой 

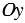
Оси 

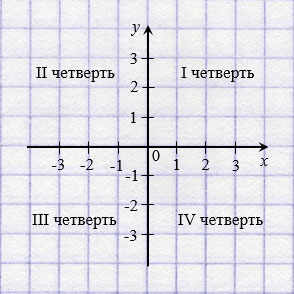
Координатные оси разбивают плоскость на четыре части, которые называют координатными четвертями и нумеруют так, как показано на рисунке ниже.
Отметим на координатной плоскости точку А. Проведем через нее прямую АВ, перпендикулярную оси абсцисс (АВ 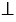
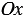
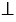
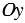
Точка В на оси 





Обратите внимание, записывая координаты точки, абсциссу всегда ставят на первое место, а ординату – на второе. Если числа 5 и 

У начала координат абсцисса и ордината равны нулю, записывают так: О(0; 0). Если точка лежит на оси абсцисс, то ее ордината равна нулю, а если на оси ординат, то нулю равна ее абсцисса. На рисунке ниже: Р(
Чтобы попасть в точку D с координатами (


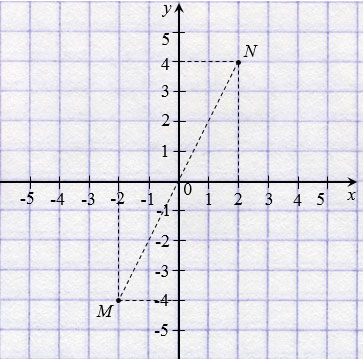
Две точки с противоположными абсциссами и ординатами симметричны относительно начала координат.
На рисунке ниже точки N(2; 4) и М(

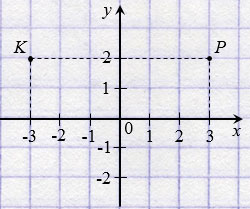
Две точки, имеющие равные ординаты и противоположные абсциссы, симметричны относительно оси ординат.
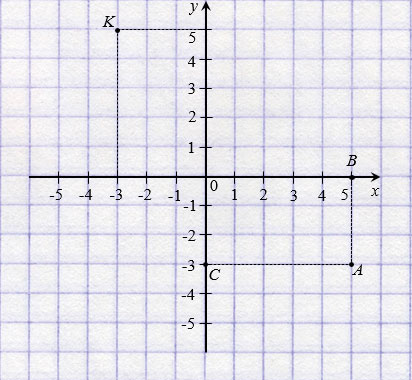
На рисунке ниже точки Р(3; 2) и К(
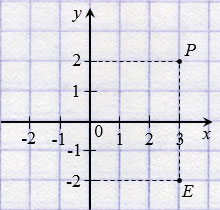
Две точки, имеющие равные абсциссы и противоположные ординаты, симметричны относительно оси абсцисс.
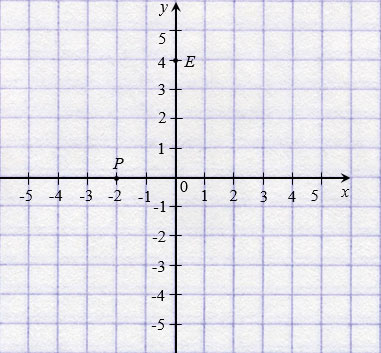
На рисунке ниже точки Р(3; 2) и Е(3; 
Советуем посмотреть:
Перпендикулярные прямые
Осевая и центральная симметрии
Параллельные прямые
Координаты на плоскости
Правило встречается в следующих упражнениях:
6 класс
Номер 1312,
Мерзляк, Полонский, Якир, Учебник
Номер 1315,
Мерзляк, Полонский, Якир, Учебник
Номер 1316,
Мерзляк, Полонский, Якир, Учебник
Номер 1317,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Задание 1391,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1418,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1434,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1466,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1547,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 782,
Мерзляк, Полонский, Якир, Учебник
Номер 822,
Мерзляк, Полонский, Якир, Учебник
Номер 827,
Мерзляк, Полонский, Якир, Учебник
Номер 859,
Мерзляк, Полонский, Якир, Учебник
Номер 861,
Мерзляк, Полонский, Якир, Учебник
Номер 870,
Мерзляк, Полонский, Якир, Учебник
Номер 994,
Мерзляк, Полонский, Якир, Учебник
Номер 995,
Мерзляк, Полонский, Якир, Учебник
Номер 1211,
Мерзляк, Полонский, Якир, Учебник
Номер 11,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 6,
Мерзляк, Полонский, Якир, Учебник
Номер 322,
Мерзляк, Полонский, Якир, Учебник
Номер 331,
Мерзляк, Полонский, Якир, Учебник
Номер 335,
Мерзляк, Полонский, Якир, Учебник
Номер 351,
Мерзляк, Полонский, Якир, Учебник
Номер 354,
Мерзляк, Полонский, Якир, Учебник
Номер 359,
Мерзляк, Полонский, Якир, Учебник
Номер 362,
Мерзляк, Полонский, Якир, Учебник
Номер 364,
Мерзляк, Полонский, Якир, Учебник
Номер 367,
Мерзляк, Полонский, Якир, Учебник
Встала задача найти положение точки относительно плоскости. Возможные положения: на плоскости, выше плоскости и ниже плоскости.
Всем знакомо уравнение плоскости.Ax + By + Cz + D = 0
И вроде бы всё просто, из курса школьной геометрии помним, если взять координаты (x, y, z) искомой точки и подставить в уравнение можно понять, где точка находится. Если =0 значит на плоскости, <0 под плоскостью, >0 над.
Хорошо, рассмотрим плоскость 2x + 3y + 4z + 5 = 0 и точку K(0, 0, 0). Получаем, 5 > 0 – точка лежит выше плоскости. Отлично, теперь умножим левую и правую часть уравнения плоскости на -1. Получаем эквивалентное уравнение -2x - 3y - 4z - 5 = 0 для нашей плоскости. Опять проверим точку K(0, 0, 0). Получаем, -5 < 0 – точка лежит ниже плоскости.
Я понимаю, что где-то совершаю глупую ошибку, но не могу понять где. Подскажите, пожалуйста.
До этого занятия мы обсуждали с вами только прямую и все, что с ней связано.
Сегодня урок посвятим изучению плоскости.
Узнаем, что называют координатной плоскостью и как получить её из обычной плоскости.
Эта информация доступна зарегистрированным пользователям
Познакомимся с прямоугольной системой координат на плоскости и разберем ее основные характеристики и особенности.
Выясним области применения и использования систем координат в практических целях и в жизни человека.
Научимся пользоваться прямоугольной системой координат на плоскости: определять координаты заданных точек и по заданным координатам точки находить ее положение на координатной плоскости.
Представим движение автомобиля по прямолинейному участку дороги.
Эта информация доступна зарегистрированным пользователям
Любой прямолинейный участок дороги легко представить с помощью координатной прямой.
Координатная прямая позволяет нам связать точки на этой прямой с числом.
Вам уже известно, как из любой прямой получить координатную прямую.
Необходимо на прямой выбрать начало отсчета, задать направление и единичный отрезок (масштаб).
Эта информация доступна зарегистрированным пользователям
В результате с помощью координатной прямой вы однозначно определите, что конкретной точке на прямой соответствует ее единственное верное значение с соответствующим знаком.
И наоборот, если известна координата точки, то можно определить положение этой точки на координатной прямой.
Таким образом, для указания местоположения точки (в нашем случае автомобиля) на прямой нужна только одна координата на координатной оси.
В жизни часто приходится устанавливать положение точки по нескольким параметрам. В таком случае для однозначного определения положения точки требуется больше информации.
Предположим, купили мы билет на концерт.
Чтобы определить расположение конкретного кресла в зале, в билете указывают адрес места: номер ряда и номер кресла в ряду.
Так как каждому месту ставится в соответствие два числа, то для однозначного определения положения точки нам не будет хватать одной координатной прямой.
Для обозначения числами точного положения точки на плоскости используют математическую модель, которую называют координатной плоскостью.
Чтобы из обычной плоскости получить координатную, необходимо на этой плоскости задать определенную систему координат.
Существует различные системы координат.
Мы рассмотрим прямоугольную систему координат на плоскости.
Прямоугольной системой координат на плоскости называют систему из двух взаимно перпендикулярных прямых с общим началом отсчета и общей масштабной единицей.
Рассмотрим основные составляющие прямоугольной системы координат.
Эта информация доступна зарегистрированным пользователям
Две перпендикулярные прямые – это координатные оси:
Горизонтальная прямая – ось абсцисс (Ох).
Вертикальная прямая – ось ординат (Оу).
Точка пересечения координатных прямых – это начало координат (начало отсчета), её обозначают точкой О(0).
Единичный отрезок выбирается чаще всего одинаковый для каждой координатной оси.
Направление осей указывается стрелкой, каждая ось подписывается буквой.
Для координатных осей обычно выбирают положительное направление, т.е. «по умолчанию» принято использовать правостороннюю систему координат, в которой за положительное направление осей принимают ось ординат, направленную вверх, и ось абсцисс, направленную вправо.
Если приходится по каким-либо причинам использовать левостороннюю прямоугольную систему координат, то данный факт оговаривают в задаче.
Положение точки на плоскости определяется двумя упорядоченными числами: координатами х и y.
Координату точки по оси Ох называют абсцисса – х.
Координату точки по оси Оу называют ордината – y.
Эта информация доступна зарегистрированным пользователям
Координату точки на плоскости записывают так:
(х; y), причем обязательно на первом месте в скобках стоит абсцисса точки (х), а на втором – ордината этой точки (y)
Например, координата точки A:
A(2;-1), где
х = 2 (координата точки по оси Ох – абсцисса точки А)
y = –1 (координата точки по оси Оу – ордината точки А)
Эта информация доступна зарегистрированным пользователям
Координаты могут иметь различные числовые значения, в том числе быть равными нулю.
Если ордината точки равна нулю, то точка лежит на оси Ох.
Если абсцисса точки равна нулю, то точка лежит на оси Оу.
Оси координат разбивают плоскость на четыре части – координатные четверти (по-другому их называют координатные углы или квадранты).
Нумерация координатных плоскостей ведется против часовой стрелки римскими цифрами I, II, III, IV.
Если точка имеет положительную координату х (х > 0) и положительную координату у (у > 0), то она лежит в I координатной четверти.
Если точка имеет отрицательную координату х (х < 0) и положительную координату у (у > 0), то она лежит во II координатной четверти.
Если точка имеет отрицательную координату х (х < 0) и отрицательную координату у (у < 0), то она лежит в III координатной четверти.
Если точка имеет положительную координату х (х > 0) и отрицательную координату у (у < 0), то она лежит в IV координатной четверти.
Эта информация доступна зарегистрированным пользователям
Например, у точки N( 1;-5) координата х положительна, а координата у отрицательная, следовательно, точка N находится в IV (четвертой) координатной четверти.
Прямоугольную систему координат называют так же декартовой системой координат.
Эта информация доступна зарегистрированным пользователям
Метод координат- это способ определения местоположения точки или тела с помощью чисел и других символов и некоторой системы координат.
Координаты и метод координат применяются и используются в различных сферах нашей жизни.
Например, координаты на картах и планах задаются числами. Для любой точки на поверхности Земли можно определить пару чисел (широту и долготу).
Координаты врача в больнице задаются номером этажа и номером кабинета.
Место в зрительном зале определяется парой чисел: номером ряда и номером кресла в ряду.
Эта информация доступна зарегистрированным пользователям
Место в поезде, указанное в билете, определяют два числа: номер вагона и номер полки.
Некоторый образ прямоугольной координатной системы прослеживается в знаменитых играх, таких как шахматы и «Морской бой».
На шахматной доске каждый квадрат имеет свои координаты: буквы латинского алфавита и цифры.
Эта информация доступна зарегистрированным пользователям
С помощью названия столбца и названия ряда (подобно координатным осям) можно определить положение шахматной фигур на игровом поле – их координаты.
Похожая ситуация складывается в игре «Морской бой».
На игровом поле (поле состоит из квадрата 10х10, разлинованного в клетку) изображаются условные корабли в виде прямоугольников и квадратов.
Задача игроков определить место положения кораблей, тем самым вычеркнуть – «уничтожить» их с поля соперника.
Такое же поле (10х10) чертится пустым, чтобы отмечать на нем координаты сбитых кораблей соперника.
Эта информация доступна зарегистрированным пользователям
Строки и столбцы задают нам подобие координатных осей, а каждый квадратик поля имеет свою координату: букву и число.
Применяется метод координат в создании различного рода таблиц.
Таблицы часто содержат большое количество упорядоченной информации.
Опять же, строки и столбцы задают нам подобие координатных осей, а координаты каждой ячейки таблицы задаются парой символов или чисел (в зависимости от специфики таблицы).
Например, таблица расписания уроков.
Конкретному времени и классу соответствует определенный урок.
Существуют специальные компьютерные программы, с помощью которых можно создавать таблицы, производить вычисления и анализировать данные.
Эта информация доступна зарегистрированным пользователям
Любой ячейке в такой таблице соответствует два символа, которые однозначно определяют ее, – это пара «число-буква».
Применение набора чисел для описания положения любой точки очень удобный инструмент.
Системы координат широко используются в современных науках и в технике.
В геодезии и картографии широта и долгота однозначно определяется положением на поверхности Земного шара.
Прямоугольная система координат применяется в военной типографии: земная поверхность на военных картах условно разбита на прямоугольники определенных размеров.
Эта информация доступна зарегистрированным пользователям
Местоположение точки на такой карте отмечается, как в Декартовой системе координат.
Кроме географических объектов военная карта несет информацию о составе войск, их дислокации и расположении, о количестве и расположении боевой техники, о составе войск, боевых действиях, происходящих и планируемых, и многое другое.
В космонавтике и астрономии с помощью особых координатных систем определяют положение звезд и иных небесных тел, вспомогательных точек на небесной сфере, а также положение и траектории летательных аппаратов.
В авиации наиболее часто используют одновременно три различные системы координат: земная, связанная и скоростная.
Земная жестко связана с Землей, применяется для определения летательного аппарата (как точки) относительно земных объектов.
Для расчета взлета, посадки и полетов на близкие расстояния используется прямоугольная система координат, в иных случаях используется более сложный расчет и система координат.
Связанная система координат служит для определения положения объектов внутри летательного аппарата.
Скоростная используется для определения положения летательного аппарата относительно воздушного потока и расчета аэродинамических параметров судна.
В морской навигации (мореплавании, судоходстве) географические координаты замеряют с помощью координатной сетки, которая состоит из взаимно параллельных линий.
Эта информация доступна зарегистрированным пользователям
Горизонтальные прямые – это линии параллелей.
Вертикальные прямые – это линии меридианов.
На левом крайнем и правом крайнем меридиане нанесена шкала географической широты точки.
На верхней и нижней параллели нанесены шкалы для измерения долготы точки.
Современные навигационные устройства, конечно, во многом превосходят бумажные из прошлого, так как они способны найти не только координаты точки, но и проложить безопасный маршрут до нее.
Даже и в этом случае нужна карта и система координат только электронная.
Программирование станков с программным управлением также тесно связана с применением системы координат.
Перемещение рабочих частей станка в пространстве при изготовлении детали задается с помощью прямоугольной системы координат.
Как вы смогли убедиться, координаты и метод координат широко используются во многих сферах нашей жизни.
Применение метода координат позволяет определить положение объекта как на плоскости, так и в пространстве.
Чтобы определить положение тела на плоскости, объект представляют точкой и находят координату этой точки на двух осях пространства.
Рассмотрим алгоритмы решения математических задач с помощью прямоугольной декартовой системы координат на плоскости.
Определение координат заданных точек на координатной плоскости.
Если на координатной плоскости задана некоторая точка А и требуется найти ее координаты, то это делается следующим образом.
Через точку А проводят две прямые: одна параллельная оси Оу, вторая – оси Ох.
Прямая, параллельная оси Оу, пересечет ось Ох в точке, которая является абсциссой точки А.
Прямая параллельная оси Ох, пересечет ось Оу в точке, которая является ординатой точки А.
Эта информация доступна зарегистрированным пользователям
Координата точки А записывается так:
А(хА;уА)
хА– абсцисса точки А (координата по оси Ох).
уА– ордината точки А (координата по оси Оу).
Построение точки на координатной плоскости по заданным координатам.
Чтобы построить точки на плоскости по заданным координатам, действуют в обратном порядке.
Отложить на оси Ох абсциссу точки А и провести перпендикулярную прямую оси Ох через отложенную координату хА.
На оси Оу отложить ординату точки А и провести перпендикулярную прямую оси Оу через отложенную координату уА.
На пересечении полученных перпендикулярных прямых получится точка А(хА; уА).
Эта информация доступна зарегистрированным пользователям
Рассмотрим простейшие примеры решения математических задач с помощью прямоугольной декартовой системы координат на плоскости.
Задача 1.
Построить точку М(-4;2) на координатной плоскости.
Решение.
Изобразим прямоугольную систему координат с единичным отрезком, в котором 1 деление = 1 единица.
Для построения точки М необходимо:
Отложить на оси Ох (влево от нуля) число (-4) и провести перпендикулярную прямую к оси Ох через эту точку.
Отложить на оси Оу число (2) и провести перпендикулярную прямую к оси Оу через эту точку.
На пересечении проведенных перпендикулярных прямых получим точку М (-4;2).
Эта информация доступна зарегистрированным пользователям
Задача 2.
Определите координату точки А в прямоугольной системе координат с единичным отрезком, в котором 1 деление = 1 единица.
Эта информация доступна зарегистрированным пользователям
Решение.
Через точку А проводим прямую параллельную оси Оу.
Прямая пересечет ось Ох в точке с координатой (-3) – это абсцисса точки А.
Через точку А проводим прямую параллельную оси Ох.
Прямая пересечет ось Оу в точке с координатой (2) – это ордината точки А.
Запишем полученную координату точки А: А(-3;2).
Эта информация доступна зарегистрированным пользователям
Задача 3.
По знакам координат точки легко определить, в какой координатной четверти находится точка.
Определите, в какой координатной четверти прямоугольной системы координат находится точка В (-21;25).
Решение.
Заметим, что абсцисса и ордината точки В имеют большие значения, поэтому определение местоположения этой точки по заданным координатам нецелесообразно.
Воспользуемся иным способом.
Нам известно, что все четверти координатной плоскости определяются знаками каждой из координат.
Координата х точки В (абсцисса точки В) отрицательное число (-21 < 0).
Значит, точка В находится слева от оси Оу, т.е. либо во II, либо в III четверти.
Координата у точки В (ордината точки В) положительное число (25 > 0).
Значит, точка В находится выше оси Ох.
Если точка находится слева от оси Оу и сверху оси Ох (х < 0,у > 0), то она находится в левом верхнем углу, а это II координатная четверть прямоугольной системы координат.
Задача 4.
Коля отметил на координатной плоскости координаты углов комнаты A(0;0), B(5;0), C(0;3), D(5;3), в которой он хочет сделать ремонт.
Сколько квадратных метров линолеума понадобится Коле для его комнаты?
Решение:
Отметим точки на координатной плоскости по заданным координатам.
Эта информация доступна зарегистрированным пользователям
Соединим эти точки, получим прямоугольник со сторонами 5 м и 3 м, – это длина и ширина Колиной комнаты.
Найдем площадь этого прямоугольника, узнаем площадь комнаты, а значит, и площадь линолеума, который потребуется Коле.
Площадь прямоугольника найдем по формуле (mathbf{S = a cdot b})
(mathbf{S = 5 cdot 3 = 15}) (м2) линолеума нужно Коле для ремонта комнаты.
Ответ: S = 15 м2
Эта информация доступна зарегистрированным пользователям
Легенды об изобретении декартовой системы координат.
Легенда первая.
Рене Декарт, посещая театры Парижа, каждый раз был удивлен неразберихе, путанице, перебранкам, а порой и вызовам на дуэль, которые возникали в связи с отсутствием четкого распределения зрителей по местам в зале.
Предложенная Декартом система нумерации, в которой каждое место получало номер ряда и порядковый номер от края ряда, решила все споры и разногласия.
Так была придумана декартова система координат.
Легенда вторая.
Однажды Рене Декарт весь день провел в кровати, размышляя о чем-то важном.
Над ним надоедливо летала и жужжала муха и не давала ему сосредоточиться.
Он стал размышлять, как бы описать математически положение мухи в любой момент времени и, предугадав ее движение, иметь возможность ее прихлопнуть…
Так была придумана декартова система координат.
Читайте также
В этой статье мы найдем ответы на вопросы о том, как создать проекцию точки на плоскость и как определить координаты этой проекции. Опираться в теоретической части будем на понятие проецирования. Дадим определения терминам, сопроводим информацию иллюстрациями. Закрепим полученные знания при решении примеров.
Проецирование, виды проецирования
Для удобства рассмотрения пространственных фигур используют чертежи с изображением этих фигур.
Проекция фигуры на плоскость – чертеж пространственной фигуры.
Очевидно, что для построения проекции существует ряд используемых правил.
Проецирование – процесс построения чертежа пространственной фигуры на плоскости с использованием правил построения.
Плоскость проекции – это плоскость, в которой строится изображение.
Использование тех или иных правил определяет тип проецирования: центральное или параллельное.
Частным случаем параллельного проецирования является перпендикулярное проецирование или ортогональное: в геометрии в основном используют именно его. По этой причине в речи само прилагательное «перпендикулярное» часто опускают: в геометрии говорят просто «проекция фигуры» и подразумевают под этим построение проекции методом перпендикулярного проецирования. В частных случаях, конечно, может быть оговорено иное.
Отметим тот факт, что проекция фигуры на плоскость по сути есть проекция всех точек этой фигуры. Поэтому, чтобы иметь возможность изучать пространственную фигуру на чертеже, необходимо получить базовый навык проецировать точку на плоскость. О чем и будем говорить ниже.
Проекция точки на плоскость
Напомним, что чаще всего в геометрии, говоря о проекции на плоскость, имеют в виду применение перпендикулярной проекции.
Произведем построения, которые дадут нам возможность получить определение проекции точки на плоскость.
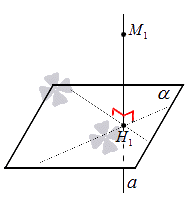
Допустим, задано трехмерное пространство, а в нем – плоскость α и точка М1, не принадлежащая плоскости α. Начертим через заданную точку М1 прямую а перпендикулярно заданной плоскости α. Точку пересечения прямой a и плоскости α обозначим как H1, она по построению будет служить основанием перпендикуляра, опущенного из точки М1 на плоскость α.
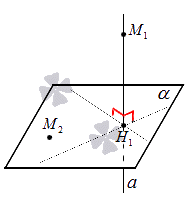
В случае, если задана точка М2, принадлежащая заданной плоскости α, то М2 будет служить проекцией самой себя на плоскость α.
Проекция точки на плоскость – это либо сама точка (если она принадлежит заданной плоскости), либо основание перпендикуляра, опущенного из заданной точки на заданную плоскость.
Нахождение координат проекции точки на плоскость, примеры
Пускай в трехмерном пространстве заданы: прямоугольная система координат Oxyz, плоскость α, точка М1(x1, y1, z1). Необходимо найти координаты проекции точки М1 на заданную плоскость.
Решение очевидным образом следует из данного выше определения проекции точки на плоскость.
Обозначим проекцию точки М1 на плоскость α как Н1. Согласно определению, H1 является точкой пересечения данной плоскости α и прямой a, проведенной через точку М1 (перпендикулярной плоскости). Т.е. необходимые нам координаты проекции точки М1 – это координаты точки пересечения прямой a и плоскости α.
Таким образом, для нахождения координат проекции точки на плоскость необходимо:
– получить уравнение плоскости α (в случае, если оно не задано). Здесь вам поможет статья о видах уравнений плоскости;
– определить уравнение прямой a, проходящей через точку М1 и перпендикулярной плоскости α (изучите тему об уравнении прямой, проходящей через заданную точку перпендикулярно к заданной плоскости);
– найти координаты точки пересечения прямой a и плоскости α (статья – нахождение координат точки пересечения плоскости и прямой). Полученные данные и будут являться нужными нам координатами проекции точки М1 на плоскость α.
Рассмотрим теорию на практических примерах.
Определите координаты проекции точки М1 (-2, 4, 4) на плоскость 2х – 3y + z – 2 = 0.
Решение
Как мы видим, уравнение плоскости нам задано, т.е. составлять его необходимости нет.
Запишем канонические уравнения прямой a, проходящей через точку М1 и перпендикулярной заданной плоскости. В этих целях определим координаты направляющего вектора прямой a. Поскольку прямая а перпендикулярна заданной плоскости, то направляющий вектор прямой a – это нормальный вектор плоскости 2х – 3y + z – 2 = 0. Таким образом, a→ = (2, -3, 1) – направляющий вектор прямой a.
Теперь составим канонические уравнения прямой в пространстве, проходящей через точку М1 (-2, 4, 4) и имеющей направляющий вектор a→ = (2, -3, 1):
x+22=y-4-3=z-41
Для нахождения искомых координат следующим шагом определим координаты точки пересечения прямой x+22=y-4-3=z-41 и плоскости 2х-3y + z – 2 = 0. В этих целях переходим от канонических уравнений к уравнениям двух пересекающихся плоскостей:
x+22=y-4-3=z-41⇔-3·(x+2)=2·(y-4)1·(x+2)=2·(z-4)1·(y-4)=-3·(z+4)⇔3x+2y-2=0x-2z+10=0
Составим систему уравнений:
3x+2y-2=0x-2z+10=02x-3y+z-2=0⇔3x+2y=2x-2z=-102x-3y+z=2
И решим ее, используя метод Крамера:
∆=32010-22-31=-28∆x=220-100-22-31=0⇒x=∆x∆=0-28=0∆y=3201-10-2221=-28⇒y=∆y∆=-28-28=1∆z=32210-102-32=-140⇒z=∆z∆=-140-28=5
Таким образом, искомые координаты заданной точки М1 на заданную плоскость α будут: (0, 1, 5).
Ответ: (0, 1, 5).
В прямоугольной системе координат Oxyz трехмерного пространства даны точки А(0, 0, 2); В(2, -1, 0); С (4, 1, 1) и М1(-1, -2, 5). Необходимо найти координаты проекции М1 на плоскость АВС
Решение
В первую очередь запишем уравнение плоскости, проходящей через три заданные точки:
x-0y-0z-02-0-1-00-24-01-01-2=0⇔xyz-22-1-241-1=0⇔⇔3x-6y+6z-12=0⇔x-2y+2z-4=0
Далее рассмотрим еще один вариант решения, отличный от того, что мы использовали в первом примере.
Запишем параметрические уравнения прямой a, которая будет проходить через точку М1 перпендикулярно плоскости АВС. Плоскость х – 2y + 2z – 4 = 0 имеет нормальный вектор с координатами (1, -2, 2), т.е. вектор a→= (1, -2, 2) – направляющий вектор прямой a.
Теперь, имея координаты точки прямой М1 и координаты направляющего вектора этой прямой, запишем параметрические уравнения прямой в пространстве:
x=-1+λy=-2-2·λz=5+2·λ
Затем определим координаты точки пересечения плоскости х – 2y + 2z – 4 = 0 и прямой
x=-1+λy=-2-2·λz=5+2·λ
Для этого в уравнение плоскости подставим:
x=-1+λ, y=-2-2·λ, z=5+2·λ
Теперь по параметрическим уравнениям x=-1+λy=-2-2·λz=5+2·λ найдем значения переменных x, y и z при λ=-1: x=-1+(-1)y=-2-2·(-1)z=5+2·(-1)⇔x=-2y=0z=3
Таким образом, проекция точки М1 на плоскость АВС будет иметь координаты (-2, 0, 3).
Ответ: (-2, 0, 3).
Отдельно остановимся на вопросе нахождения координат проекции точки на координатные плоскости и плоскости, которые параллельны координатным плоскостям.
Пусть задана точки М1(x1, y1, z1) и координатные плоскости Oxy, Оxz и Oyz. Координатами проекции этой точки на данные плоскости будут соответственно: (x1, y1, 0), (x1, 0, z1) и (0, y1, z1). Рассмотрим также плоскости, параллельные заданным координатным плоскостям:
Cz+D=0⇔z=-DC, By+D=0⇔y=-DB
И проекциями заданной точки М1 на эти плоскости будут точки с координатами x1,y1, -DC, x1, -DB, z1 и -DA, y1, z1.
Продемонстрируем, как был получен этот результат.
В качестве примера определим проекцию точки М1(x1, y1, z1) на плоскость Ax+D=0 . Остальные случаи – по аналогии.
Заданная плоскость параллельна координатной плоскости Oyz и i→= (1, 0, 0) является ее нормальным вектором. Этот же вектор служит направляющим вектором прямой, перпендикулярной к плоскости Oyz. Тогда параметрические уравнения прямой, проведенной через точку M1 и перпендикулярной заданной плоскости, будут иметь вид:
x=x1+λy=y1z=z1
Найдем координаты точки пересечения этой прямой и заданной плоскости. Подставим сначала в уравнение Аx+ D = 0 равенства: x=x1+λ, y=y1, z=z1 и получим: A·(x1+λ)+D=0⇒λ=-DA-x1
Затем вычислим искомые координаты, используя параметрические уравнения прямой при λ=-DA-x1:
x=x1+-DA-x1y=y1z=z1⇔x=-DAy=y1z=z1
Т.е., проекцией точки М1(x1, y1, z1) на плоскость будет являться точка с координатами -DA, y1, z1.
Необходимо определить координаты проекции точки М1(-6, 0, 12) на координатную плоскость Oxy и на плоскость 2y-3=0 .
Решение
Координатной плоскости Oxy будет соответствовать неполное общее уравнение плоскости z = 0. Проекция точки М1 на плоскость z = 0 будет иметь координаты (-6, 0, 0).
Уравнение плоскости 2y-3=0 возможно записать как y=322 . Теперь просто записать координаты проекции точки M1(-6, 0, 12) на плоскость y=322 :
-6, 322, 12
Ответ: (-6, 0, 0) и -6, 322, 12