Как найти полупериметр треугольника зная площадь – Сайт, где вы сможете решить свои вопросы

Фо́рмула Герона — формула для вычисления площади треугольника $S$ по длинам его сторон $a,b,c$ :

${displaystyle S={sqrt {p(p-a)(p-b)(p-c)}}}$ ,

где $p$ — полупериметр треугольника: ${displaystyle p={tfrac {1}{2}}cdot (a+b+c)}$ .

Формула содержится в «Метрике» Герона Александрийского (I век н. э.) и названа в его честь (хотя она была известна ещё Архимеду). Герон интересовался треугольниками с целочисленными сторонами, площади которых тоже являются целыми, такие треугольники носят название героновых, простейшим героновым треугольником является египетский треугольник.

Доказательство 1 (тригонометрическое):

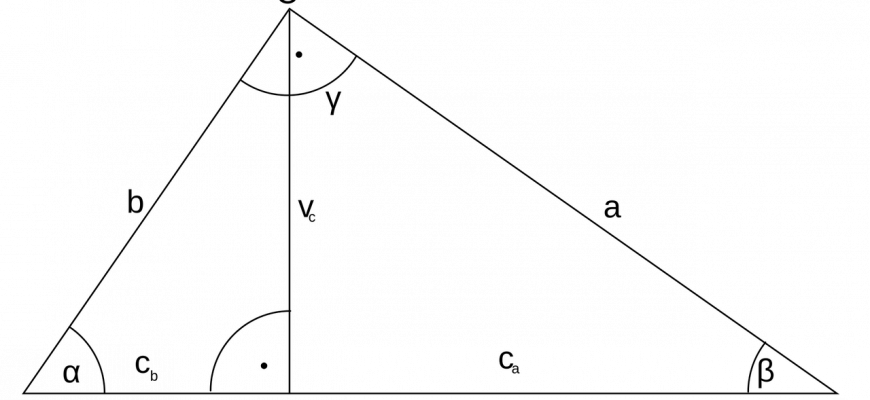
Доказательство 2 (на основе теоремы Пифагора):

Треугольник со сторонами a, b, c и высотой

h, разделяющей основание

c на

d и (c − d).

По теореме Пифагора имеем следующие равенства для гипотенуз: a² = h² + (c − d)² и b² = h² + d² — см. рисунок справа. Вычитая из первого равенства второе, получаем a² − b² = c² − 2cd. Это уравнение позволяет нам выразить d через стороны треугольника:

${displaystyle d={frac {-a^{2}+b^{2}+c^{2}}{2c}}}$

Для высоты h у нас было равенство h² = b² − d², в которое можно подставить полученное выражение для d и применить формулы для квадратов:

${displaystyle {begin{aligned}h^{2}&=b^{2}-left({frac {-a^{2}+b^{2}+c^{2}}{2c}}right)^{2}={frac {(2bc-a^{2}+b^{2}+c^{2})(2bc+a^{2}-b^{2}-c^{2})}{4c^{2}}}\&={frac {((b+c)^{2}-a^{2})(a^{2}-(b-c)^{2})}{4c^{2}}}={frac {(b+c-a)(b+c+a)(a+b-c)(a-b+c)}{4c^{2}}}\end{aligned}}}$

Замечая, что ${displaystyle b+c-a=2p-2a}$ , $a+b+c=2p$ , $a+b-c=2p-2c$ , ${displaystyle a-b+c=2p-2b}$ , получаем:

${displaystyle {begin{aligned}h^{2}&={frac {2(p-a)cdot 2pcdot 2(p-c)cdot 2(p-b)}{4c^{2}}}={frac {4p(p-a)(p-b)(p-c)}{c^{2}}}end{aligned}}}$

Используя основное равенство для площади треугольника ${displaystyle S={frac {ch}{2}}}$ и подставляя в него полученное выражение для h, в итоге имеем:

${displaystyle {begin{aligned}S={sqrt {{frac {c^{2}}{4}}cdot {frac {4p(p-a)(p-b)(p-c)}{c^{2}}}}}={sqrt {p(p-a)(p-b)(p-c)}}end{aligned}}}$

ч.т.д.

Вариации и обобщения[править | править код]

Формулу Герона можно записать с помощью определителя в виде^[1]:

$-16S^{2}={begin{vmatrix}0&a^{2}&b^{2}&1\a^{2}&0&c^{2}&1\b^{2}&c^{2}&0&1\1&1&1&0end{vmatrix}}={begin{vmatrix}a&b&c&0\b&a&0&c\c&0&a&b\0&c&b&aend{vmatrix}}$

Первый определитель последней формулы является частным случаем определителя Кэли — Менгера^[en] для вычисления гиперобъёма симплекса.

через длины высот $h_{a}$ , $h_{b}$ и $h_{c}$ и полусумму их обратных величин $H=(h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1})/2$ ^[3]:

$S^{-1}=4{sqrt {H(H-h_{a}^{-1})(H-h_{b}^{-1})(H-h_{c}^{-1})}}$ ;

через углы треугольника $alpha$ , $beta$ и $gamma$ , полусумму их синусов ${displaystyle s=(sin alpha +sin beta +sin gamma )/2}$ и диаметр описанной окружности ${displaystyle D={tfrac {a}{sin alpha }}={tfrac {b}{sin beta }}={tfrac {c}{sin gamma }}}$ ^[4]:

$S=D^{2}{sqrt {s(s-sin alpha )(s-sin beta )(s-sin gamma )}}.$

Площадь вписанного в окружность четырёхугольника вычисляется по формуле Брахмагупты:

$S={sqrt {(p-a)(p-b)(p-c)(p-d)}}$ ,

где $p={frac {a+b+c+d}{2}}$ — полупериметр четырёхугольника; в данном случае треугольник оказывается предельным случаем вписанного четырёхугольника при устремлении длины одной из сторон к нулю. Та же формула Брахмагупты через определитель^[5]:

$S={frac {1}{4}}{sqrt {-{begin{vmatrix}a&b&c&-d\b&a&-d&c\c&-d&a&b\-d&c&b&aend{vmatrix}}}}$

где:

${displaystyle {begin{aligned}a&={sqrt {xYZ}}\b&={sqrt {yZX}}\c&={sqrt {zXY}}\d&={sqrt {xyz}}\X&=(w-U+v),(U+v+w)\x&=(U-v+w),(v-w+U)\Y&=(u-V+w),(V+w+u)\y&=(V-w+u),(w-u+V)\Z&=(v-W+u),(W+u+v)\z&=(W-u+v),(u-v+W)end{aligned}}}$ .

где $theta _{s}={frac {theta _{a}+theta _{b}+theta _{c}}{2}}$ — полупериметр.

Примечания[править | править код]

↑ Weisstein, Eric W. Heron’s Formula. Архивная копия от 5 сентября 2015 на Wayback Machine From MathWorld–A Wolfram Web Resource.
↑ Benyi, Arpad, “A Heron-type formula for the triangle, « Mathematical Gazette» 87, July 2003, 324—326.
↑ Mitchell, Douglas W., “A Heron-type formula for the reciprocal area of a triangle, ” Mathematical Gazette 89, November 2005, 494.
↑ Mitchell, Douglas W., “A Heron-type area formula in terms of sines, ” Mathematical Gazette 93, March 2009, 108—109.
↑ Стариков В. Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов. Выпуск 1/ Гл ред. Романова И .В Чебоксары: ЦДИП «INet», 2014. С. 37-39
↑ W. Kahan, «What has the Volume of a Tetrahedron to do with Computer Programming Languages?», [1] Архивная копия от 27 июня 2013 на Wayback Machine, pp. 16-17.
↑ Маркелов С. Формула для объёма тетраэдра// Математическое просвещение. Вып. 6. 2002. С. 132

Литература[править | править код]

§ 258 в А. П. Киселёв, Геометрия по Киселёву, arΧiv:1806.06942 [math.HO].
Николаев Н. О площади треугольника // В.О.Ф.Э.М.. — 1890. — № 108. — С. 227—228.
Raifaizen, Claude H. A Simpler Proof of Heron’s Formula (англ.) // Mathematics Magazine : magazine. — 1971. — Vol. 44. — P. 27—28. — доказательство формулы Герона на основе теоремы Пифагора

Источник

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Треугольник – это многоугольник с тремя сторонами.

По формуле Герона

Формула Герона для нахождения площади треугольника:

Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:

Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Площадь прямоугольного треугольника

Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.

Формула нахождения площади прямоугольного треугольника через катеты:

Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.

Формула нахождения площади равнобедренного треугольника через две стороны:

Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:

Площадь равностороннего треугольника через стороны

Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.

Формула нахождения площади равностороннего треугольника через сторону:

Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:

Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

Please wait.

We are checking your browser. mathvox.ru

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d6f4953aed87a6d • Your IP : 85.95.188.35 • Performance & security by Cloudflare

Площадь треугольника через стороны

Площадь треугольника через стороны — это
площадь треугольника, которая выражена через
три стороны треугольника и полупериметр.

Полупериметр — это половина суммы
длин всех сторон треугольника.

Площадь любого треугольника можно рассчитать по
разным формулам. Одна из популярных формул:

С помощью этой формулы можно найти площадь
треугольника зная длину основания и высоту.
Но, иногда требуется найти площадь треугольника,
зная только стороны треугольника. Так, как у
каждого треугольника три стороны, то соответственно
три длины. Но, как же найти площадь?

Площадь треугольника через стороны легко рассчитать
зная Формулу Герона.Герон — греческий математик, в
честь которого и была названа эта формула. В чем суть
формулы Герона? Как найти площадь треугольника через длины сторон?

Площадь произвольного треугольника равна квадратному
корню из произведения полупериметра на разницу
между полупериметром и стороной a, полупериметром
и стороной b, полупериметром и стороной c.

Можно сделать вывод, что, чтобы рассчитать площадь треугольника
по Формуле Герона, нужно знать все стороны данного треугольника.

Формула Герона:

a, b, c — длины сторон треугольника;
p — полупериметр;
S — площадь;

Формула полупериметра:

Обобщение площади треугольника через стороны:

Подставив в вышеперечисленные формулы длины всех сторон,
можно найти площадь любого треугольника. С помощью формулы
площади треугольника через три стороны, можно также
найти не только площадь, но и периметр.

[spoiler title=”источники:”]

http://mathvox.ru/geometria/treugolniki/treugolniki-glava-1/perimetr-poluperimetr-treugolnika/

http://colibrus.ru/ploschad-treugolnika-cherez-storony/

[/spoiler]

Источник

Содержание

– Как найти Полупериметр если есть периметр?
– Как найти площадь треугольника зная его периметр?
– Как найти Полупериметр трапеции?
– Что такое площадь треугольника 3 класс?
– Что такое площадь 3 класс?

Чтобы найти полупериметр треугольника, нужно сложить длины всех его сторон, и полученный результат разделить на два.

Как найти Полупериметр если есть периметр?

Если периметр – это сумма длин всех сторон фигуры, то полупериметр – сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках – (a+b)).

Как найти площадь треугольника зная его периметр?

Площадь треугольника = a * h/2. Периметр треугольника = a + b + c.

Как найти Полупериметр трапеции?

Трапеция – это четырехугольник с двумя параллельными сторонами. Чтобы найти периметр трапеции, нужно сложить длины всех четырех сторон. Зачастую в задачах длины некоторых сторон не даны, но известны другие величины, например, высота или угол трапеции.

Что такое площадь треугольника 3 класс?

Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.

Что такое площадь 3 класс?

Площадь – внутренняя часть любой плоской геометрической фигуры. Квадрат – это прямоугольник, у которого все стороны равны. … Квадратный сантиметр – квадрат со стороной 1 сантиметр.

Интересные материалы:

Как долго принимать аллохол?
Как долго проходят симптомы цистита?
Как долго проходит корочка от Микроблейдинга?
Как долго проходит красный загар?
Как долго растет груша?
Как долго шпаклевать стены?
Как долго сходят корочки после Пудрового напыления бровей?
Как долго смывается тоник для волос?
Как долго смывается тоник с волос?
Как долго смывается тонировка с волос?

Источник

Содержание материала

Треугольники [ править ]
Видео
Если известны длины трех сторон
Для прямоугольного треугольника
Площадь треугольника по гипотенузе и острому углу
Площадь прямоугольного треугольника по катету и прилежащему углу
Если он равнобедренный
Как найти Полупериметр трапеции?

Треугольники [ править ]

В любом треугольнике расстояние вдоль границы треугольника от вершины до точки на противоположном крае, которой касается вневписанная окружность, равно полупериметру.

Полупериметр чаще всего используется для треугольников; формула для полупериметра треугольника со сторонами a , b и c имеет вид

Видео

Если известны длины трех сторон

Делайте так:

Найдите периметр. Для этого сложите все три стороны.
Найдите полупериметр – разделите периметр на два. Запомните значение.
Отнимите от полупериметра длину первой стороны. Запомните.
Отнимите от полупериметра длину второй стороны. Тоже запомните.
Отнимите от полупериметра длину третьей стороны. И ее запомните.
Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Для прямоугольного треугольника

Для прямоугольного треугольника чаще всего используют одну формулу — половину произведения катетов. Потому что их всегда можно найти с помощью правил тригонометрии или теоремы Пифагора.

, где , — стороны.

Площадь треугольника по гипотенузе и острому углу

, где — гипотенуза, — любой из прилегающих острых углов.

Гипотенузой принято называть сторону, которая лежи

Гипотенузой принято называть сторону, которая лежит напротив прямого угла.

Площадь прямоугольного треугольника по катету и прилежащему углу

, где — катет, — прилежащий угол.

Катетом принято называть одну из двух сторон, обра

Катетом принято называть одну из двух сторон, образующих прямой угол.

Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Как найти Полупериметр трапеции?