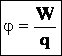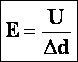Понятие электрического потенциала является одним из важных основ теории электростатики и электродинамики. Понимание его сущности является необходимым условием для дальнейшего изучения этих разделов физики.
Содержание
- 1 Что такое электрический потенциал
- 2 Свойства потенциала
- 3 Разность потенциалов
- 4 Эквипотенциальные поверхности
Что такое электрический потенциал
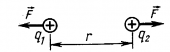
Пусть в поле, создаваемым неподвижным зарядом Q, помещён единичный заряд q, на который действует сила Кулона F=k*Qq/r.
Здесь и далее k=((1/4)*π* ε0* ε), где ε0 — электрическая постоянная (8,85*10-12 Ф/м), а ε – диэлектрическая постоянная среды.
Внесённый заряд под действием этой силы может перемещаться, а сила при этом совершит определенную работу. Это означает, что система из двух зарядов обладает потенциальной энергией, зависящей от величины обоих зарядов и расстояния между ними, причём величина этой потенциальной энергии не зависит от величины заряда q. Здесь и вводится определение электрического потенциала – он равен отношению потенциальной энергии поля к величине заряда:
φ=W/q,
где W – потенциальная энергия поля, создаваемого системой зарядов, а потенциал является энергетической характеристикой поля. Чтобы переместить заряд q в электрическом поле на какое-то расстояние, надо затратить определённую работу на преодоление кулоновских сил. Потенциал точки равен работе, которую надо затратить для перемещения единичного заряда из этой точки в бесконечность. При этом надо отметить, что:
- эта работа будет равна убыли потенциальной энергии заряда (A=W2-W1);
- работа не зависит от траектории перемещения заряда.
В системе СИ единицей измерения потенциала является один Вольт (в русскоязычной литературе обозначается буквой В, в зарубежной – V). 1 В=1Дж/1 Кл, то есть, можно говорить о потенциале точки в 1 вольт, если для перемещения заряда в 1 Кл в бесконечность потребуется совершить работу в 1 Джоуль. Название выбрано в честь итальянского физика Алессандро Вольта, внесшего значительный вклад в развитие электротехники.
Чтобы наглядно представить, что такое потенциал, его можно сравнить с температурой двух тел или температурой, замеренной в разных точках пространства. Температура служит мерой нагрева объектов, а потенциал – мерой электрической заряженности. Говорят, что одно тело нагрето более другого, также можно сказать, что одно тело заряжено более, а другое – менее. Эти тела обладают разным потенциалом.
Значение потенциала зависит от выбора системы координат, поэтому требуется какой-то уровень, который надо принять за ноль. При измерении температуры за базовую границу можно принять, например, температуру тающего льда. Для потенциала за нулевой уровень обычно принимают потенциал бесконечно удаленной точки, но для решения некоторых задач за нулем можно считать, например, потенциал земли или потенциал одной из обкладок конденсатора.
Свойства потенциала
Среди важных свойств потенциала надо отметить следующие:
- если поле создается несколькими зарядами, то потенциал в конкретной точке будет равен алгебраической (с учетом знака заряда) сумме потенциалов, создаваемых каждым из зарядов φ=φ1+φ2+φ3+φ4+φ5+…+φn;
- если расстояния от зарядов таковы, что сами заряды можно считать точечными, то суммарный потенциал считается по формуле φ=k*(q1/r1+q2/r2+q3/r3+…+qn/rn), где r – расстояние от соответствующего заряда то рассматриваемой точки.
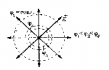
Если поле образовано электрическим диполем (двумя связанными зарядами противоположного знака), то потенциал в любой точке, находящейся на расстоянии r от диполя будет равен φ=k*p*cosά/r2, где:
- p – электрическое плечо диполя, равное q*l, где l – расстояние между зарядами;
- r – расстояние до диполя;
- ά – угол между плечом диполя и радиус-вектором r.
Если точка лежит на оси диполя, то cosά=1 и φ=k*p/r2.
Разность потенциалов
Если две точки обладают определённым потенциалом, и если они не равны, то говорят о том, что между двумя точками существует разность потенциалов. Разность потенциалов возникает между точками:
- потенциал которых определяется зарядами разных знаков;
- точкой с потенциалом от заряда любого знака и точкой с нулевым потенциалом;
- точками, имеющими потенциал равного знака, но отличающимися по модулю.
То есть, разность потенциалов не зависит от выбора системы координат. Можно провести аналогию с бассейнами с водой, расположенными на разной высоте относительно нулевой отметки (например, уровня моря).
Вода каждого бассейна имеет определенную потенциальную энергию, но если соединить два любых бассейна трубкой, то в каждой из них возникнет поток воды, расход которой определяется не только размерами трубки, но и разностью потенциальных энергий в гравитационном поле Земли (то есть, разностью высот). Абсолютное значение потенциальных энергий значения в данном случае не имеет.
Точно так же, если соединить проводником две точки с разным потенциалом, по нему потечёт электрический ток, определяемый не только сопротивлением проводника, но и разностью потенциалов (но не их абсолютным значением). Продолжая аналогию с водой, можно сказать, что вода в верхнем бассейне скоро закончится, и если не найдется той силы, которая переместит воду обратно наверх (например, насоса), то и поток очень быстро прекратится.
Так и в электрической цепи – чтобы поддерживать разность потенциалов на определенном уровне, потребуется сила, переносящая заряды (точнее, носители зарядов) к точке с наибольшим потенциалом. Такая сила называется электродвижущей силой и сокращенно обозначается ЭДС. ЭДС может носить различную природу – электрохимическую, электромагнитную и т.п.
На практике имеет значение в основном разность потенциалов между начальной и конечной точками траектории движения носителей зарядов. В этом случае эту разность называют напряжением, и оно в СИ также измеряется в вольтах. О напряжении в 1 Вольт можно говорить, если поле совершает работу в 1 Джоуль при перемещении заряда в 1 Кулон из одной точки в другую, то есть 1В=1Дж/1Кл, и Дж/Кл также может являться единицей измерения разности потенциалов.
Эквипотенциальные поверхности
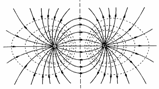
Если потенциал нескольких точек одинаков, и эти точки образуют поверхность, то такая поверхность называется эквипотенциальной. Таким свойством обладает, например, сфера, описанная вокруг электрического заряда, ведь электрическое поле убывает с расстоянием одинаково во все стороны.
Все точки этой поверхности имеют одинаковую потенциальную энергию, поэтому при перемещении заряда по такой сфере работа затрачиваться не будет. Эквипотенциальные поверхности систем из нескольких зарядов имеют более сложную форму, но у них есть одно интересное свойство – они никогда не пересекаются. Силовые линии электрического поля всегда перпендикулярны поверхностям с одинаковым потенциалом в каждой их точке. Если эквипотенциальную поверхность рассечь плоскостью, получится линия равных потенциалов. Она имеет те же свойства, что и эквипотенциальная поверхность. На практике равный потенциал имеют, например, точки на поверхности проводника, помещенного в электростатическое поле.
Разобравшись с понятием потенциала и разности потенциалов, можно приступать к дальнейшему изучению электрических явлений. Но не ранее, потому что без понимания базовых принципов и понятий углубить знания не получится.
-
Выражение потенциала любой точки схемы через потенциалы соседних точек.
Рассмотрим
на примере схемы рис. 15.
Рис.
15. Схема электрической цепи
Перед
расчетом произвольно выбираются
направления токов во всех ветвях и
больше не меняются в процессе расчета.
Найдем
разность потенциалов между точками d
и n
на пути ncabmd.
;
.
(18)
При
движении от точки n
к точке c
потенциал скачком возрастает на величину
ЭДС .
На участках ca
и ab
движемся против тока, т.е. в сторону
возрастания потенциала, поэтому падения
напряжения
и
входят в выражение (18) со знаком «плюс».
Далее на участке bm
скачок потенциала, поэтому падение
напряжения
входит в выражение (18) со знаком «плюс».
Разность
потенциалов между точками d
и n
по кратчайшему пути будет:
Udn
=
I3R3.
(19)
Знак
«плюс» соответствует возрастанию
потенциала при движении от точки n
к точке d
по току.
Если
при расчете по двум разным путям между
одними и теми же точками получается
одинаковая разность потенциалов, то
можно считать, что токи рассчитаны
верно. Это дополнительное средство
проверки правильности расчета.
Найдем
теперь разность потенциалов между
точками b
и m
на пути mdncab:
Ubm
=
I2R2
– I3R3
+
E3
+ I6R6
+ I4R4;
(20)
. (21)
-
Первый и второй законы Кирхгофа. Составление уравнений для расчета токов в схемах при наличии в них источников эдс и тока.
Первый
закон Кирхгофа формируется следующим
образом: алгебраическая сумма токов,
сходящихся в узле равна нулю. Математически
это записывается так:
.
(22)
Здесь
n
– число узлов, для которых составляются
уравнения по первому закону Кирхгофа.
Положительными
считаются токи, подходящие к узлу,
отрицательными – отходящие от узла.
В
схеме рис. 15 пять узлов: a,
b,
c,
d,
n.
Количество уравнений, которые нужно
составить по первому закону Кирхгофа,
равно числу узлов без единицы:
. (23)
Здесь
У=5
число
узлов.
Узлы,
для которых составляются уравнения,
выбираются произвольно.
Составим
четыре уравнения по первому закону
Кирхгофа для узлов a,
b,
c,
d:
-
;
(24)
b)
;
(25)
c)
;
(26)
d)
–
.
(27)
Уравнение
для последнего узла не составляется,
так как оно может быть выведено из ранее
составленных уравнений (24), (25), (26) и (27).
В
схеме рис. 15 число ветвей В
равно семи, оно всегда равно числу
неизвестных токов.
Второй
закон Кирхгофа формулируется следующим
образом: алгебраическая сумма падений
напряжений вдоль любого замкнутого
контура равно алгебраической сумме ЭДС
того же контура.
.
(28)
Здесь
n
– число контуров, для которых составляются
уравнения по второму закону Кирхгофа.
Любой
замкнутый путь в схеме называется
электрическим контуром. Ветвь с источником
тока не учитывается при подсчете числа
контуров.
Так
в схеме рис. 15 шесть контуров: admba,
acnda,
abca,
cndabc,
cadmbc
и cndmbc.
Независимым
контуром называется такой контур, в
который входит хотя бы одна новая ветвь,
не вошедшая в предыдущие контуры.
Независимых
контуров на схеме рис. 15 всего три: admba,
adnca,
abca.
Контуры
,
и
не
являются независимыми контурами, так
как входящие в них ветви уже использованы
при составлении первых трех контуров.
Выберем
также произвольно направления обхода
независимых контуров, например, все по
часовой стрелке.
Число
уравнений ,
которые
нужно составить по второму закону
Кирхгофа равно числу ветвей
минус ,
т.е. число уравнений, составленных по
первому закону Кирхгофа
. (29)
Это
всегда равно числу независимых контуров
. (30)
При
составлении уравнений по второму закону
Кирхгофа падение напряжения следует
считать положительным, если направление
тока в данной ветви совпадает с
направлением обхода контура, и
отрицательным – если ток не совпадает
с направлением обхода.
Составим
уравнения по второму закону Кирхгофа
для выбранных независимых контуров:
admba
;
(31)
abca ;
(32)
acnda
I1R1
+ I6R6
– I3R3
= -E3.
(33)
ЭДС
контура берутся со знаком «плюс», если
их направления совпадают с направлением
обхода контура, и «минус» – если не
совпадают.
17
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Потенциал. Разность потенциалов.
Разность потенциалов (напряжение) между 2-мя точками поля равняется отношению работы поля по перемещению заряда из начальной точки в конечную к этому заряду:
,
Так как работа по перемещению заряда в потенциальном поле не зависит от формы траектории, то, зная напряжение между двумя точками, мы определим работу, которая совершается полем по перемещению единичного заряда.
Если есть несколько точечных зарядов, значит, потенциал поля в некоторой точке пространства определяется как алгебраическая сумма потенциалов электрических полей каждого заряда в данной точке:
.
Эквипотенциальной поверхностью, или поверхностью равного потенциала, является поверхность, для любых точек которой разность потенциалов равна нулю. Это означяет, что работа по перемещению заряда по такой поверхности равна нулю, следовательно, линии напряженности электрического поля перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности однородного поля представляют собой плоскости, а точечного заряда — концентрические сферы.
Вектор напряженности 

Напряжение и напряженность однородного поля .
В однородном электрическом поле напряженность E в каждой точке одинакова, и работа A по перемещению заряда q параллельно на расстояние d между двумя точками с потенциалами φ1, и φ2 равна:
,
.
Т.о., напряженность поля пропорциональна разности потенциалов и направлена в сторону уменьшения потенциала. Поэтому положительный заряд будет двигаться в сторону уменьшения потенциала, а отрицательный — в сторону его увеличения.
Единицей напряжения (разности потенциалов) является вольт. Исходя из формулы 

Электрический потенциал простыми словами: формулы, единица измерения
Электрический потенциал – это скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.
Если вы хотите расширить свои знания об электрическом потенциале или сначала узнать, что такое электрический потенциал, то вы пришли по адресу.
Простое объяснение
В классической механике рассмотрение проблемы с точки зрения энергии может значительно упростить ситуацию по сравнению с рассмотрением ее с точки зрения сил, действующих на систему. В частности, в этом контексте существенную роль играет тот факт, что энергия является сохраняющейся переменной.
Также в классической электродинамике рассмотрение на энергетическом уровне оказывается очень полезным. Поэтому электрический потенциал φ (также называемый электростатическим потенциалом) определяется как отношение потенциальной энергии Eпот пробного электрического заряда и его величины электрического заряда q: φ = Eпот / q .
Возможность определения такого электрического потенциала обусловлена тем, что электрическое поле E распределения заряда и результирующая электростатическая сила Fc на пробном электрическом заряде является консервативной силой, подобной гравитационной силе.
Электрический потенциал имеет единицу измерения вольт В или также джоуль на кулон Дж / Кл .
Формулы
В этом разделе мы познакомим вас с двумя важными формулами для электрического потенциала определенных распределений электрических зарядов. Мы также кратко обсудим аналогию между электрическим потенциалом и гравитацией.
Пластинчатый конденсатор
Мы рассматриваем ситуацию, когда две плоские пластины расположены параллельно на расстоянии d друг от друга. Кроме того, пусть одна из двух пластин заряжена положительно, а другая – отрицательно. Такая комбинация также называется пластинчатым конденсатором. Обозначим точку на положительной пластине через A, а точку на отрицательной пластине через B. Тогда для разности потенциалов между этими двумя точками получим:
Здесь E – величина электрического поля между двумя пластинами, которое предполагается однородным. Такая разность потенциалов также называется электрическим напряжением, которое существует между этими двумя точками.
Из этого уравнения видно, что электрический потенциал на положительно заряженной пластине (пластина A) выше, чем потенциал на отрицательно заряженной пластине (пластина B). Поэтому положительный заряд в пластинчатом конденсаторе перемещается к отрицательной пластине. В общем случае электрическое поле – а значит, и направление движения положительного заряда – направлено в ту сторону, в которой электрический потенциал убывает быстрее всего.
Рис. 1. Пластинчатый конденсатор
Аналогия с гравитационным полем
Если умножить уравнение (приведенное выше в статье) на величину электрического заряда q пробного электрического заряда и предположить, что отрицательно заряженная пластина имеет электрический потенциал, равный нулю, то электрическая потенциальная энергия на расстоянии h от пластины равна:
Eпот. эл = q * φ = q * E * h
Здесь φ обозначает электрический потенциал в точке пробного электрического заряда.
Сравним это уравнение с потенциальной энергией в однородном гравитационном поле:
Eпот. гр = m * g * h .
Мы определяем, что количество заряда электрического q играет роль массы m, а величина электрического поля E играет роль гравитационного ускорения g. Масса, находящаяся на высоте h над землей, ускоряется по направлению к земле под действием земного притяжения.
Таким образом, масса движется в том направлении, в котором уменьшается ее потенциальная энергия. Аналогично, положительный электрический заряд движется в направлении, в котором его электрическая потенциальная энергия будет уменьшаться. Поскольку электрическая потенциальная энергия и электрический потенциал линейно связаны, это наблюдение аналогично тому, что положительно заряженная частица движется в направлении уменьшения электрического потенциала.
Рис. 2. Аналогия с гравитационным полем
Подобно потенциальной энергии, только разность потенциалов имеет физический смысл, поскольку при определении электрического потенциала необходимо произвольно определить точку отсчета, от которой затем можно обозначить другие точки в пространстве. В этом смысле электрический потенциал сам по себе не имеет реального физического смысла, поскольку для данной точки в пространстве его значение можно изменить, выбрав другую точку отсчета. Таким образом, электрический потенциал ведет себя подобно высоте, потому что вы не можете говорить о высоте, пока у вас нет точки отсчета.
На топографической карте – пути, вдоль которых высота не меняется, называются изолиниями. Аналогично, пути, вдоль которых электрический потенциал постоянен, называются эквипотенциальными линиями.
Заряженные частицы
Предположим, что частица с зарядом q находится в начале выбранной нами системы координат. Пусть положение другой точки равно r и пусть r – расстояние между двумя точками. Для электрического потенциала в точке r действует следующее соотношение:
φ (r) = q / 4 * π * ε0 * r ,
здесь ε0 – электрическая постоянная.
В этом уравнении предполагается, что под действием электрического поля положительный пробный электрический заряд переносится из бесконечности в положение r.
Примеры задач
Наконец, давайте вместе рассчитаем небольшой пример. Предположим, что электрон ускоряется от отрицательно заряженной пластины к положительно заряженной через разность потенциалов 2000 В. Как изменяется потенциальная энергия электрона?
Для разности электрических потенциалов между двумя пластинами: φB – φA = ΔEпот / q , преобразованной в искомое изменение потенциальной энергии, получаем:
Величина электрического заряда электрона равна qe = e = – 1,6 * 10 -19 Кл и поэтому получаем:
ΔEпот = e * ( φB – φA ) = – 1,6 * 10 -19 Кл * 2000 В = -3,2 * 10 -19 Дж.
Обратите внимание, что [ В ] = Дж / Кл. Кроме того, мы предположили, что пластина с точкой B заряжена положительно, поэтому перед 2000 В нет знака минус. Расчет показывает, что потенциальная энергия электрона уменьшается.
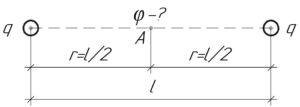
Найти потенциал электрического поля в точке, лежащей посредине между двумя
Найти потенциал электрического поля в точке, лежащей посредине между двумя зарядами по 50 нКл, расположенными на расстоянии 1 м в вакууме.
Задача №6.3.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
Так как заряды одинаковы, и они находятся на одинаковом расстоянии (r) от точки A, в которой нужно определить потенциал, значит потенциалы электрических полей в точке A, создаваемых каждым зарядом, также одинаковы. Это видно из формулы:
Здесь (k) – коэффициент пропорциональности, равный 9·10 9 Н·м 2 /Кл 2 .
Учитывая, что точка A находится посредине между двумя зарядами ((r=frac)), то:
Искомый потенциал (varphi) равен сумме потенциалов электрических полей в точке A, создаваемых каждым зарядом, поскольку потенциал – величина скалярная. Учитывая вышесказанное, имеем:
В итоге решение задачи в общем виде выглядит так:
Ответ: 1,8 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Для школьников.
Теория вопроса.
Если электрическое поле создаётся системой неподвижных зарядов, то при расчётах полей пользуются принципом суперпозиции: находят поля, создаваемые каждым зарядом в отдельности, затем их суммируют. Можно мысленно в точку поля помещать пробный (положительный) заряд. Куда направлена сила, действующая на этот заряд со стороны данного заряда, туда же направлен вектор напряжённости.
Учитываем, что потенциал алгебраическая величина. Его знак совпадает со знаком заряда, создающего поле.
В задаче 3 можно представить, что речь идёт о конденсаторе. Между заряженными разноимённо пластинами электрическое поле существует (получена формула для его расчёта), а вне пластин конденсатора электрического поля нет.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Занятие 49. Потенциал точки электростатического поля. Разность потенциалов.
Следующая запись: Как графически изображают электростатические поля. Две характеристики поля.
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (начиная с электростатики) даны в Занятии 45.
|
Потенциал. Разность потенциалов. Напряжение. |
|
|
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: – энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. |
|
|
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора. |
|
|
– следствие принципа суперпозиции полей (потенциалы складываютсяалгебраически). |
|
|
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах: |
|
|
Разность потенциалов |
|
|
|
|
|
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат! |
|
|
Единица разности потенциалов
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж. |
|
|
Связь между напряженностью и напряжением. |
|
|
Из доказанного выше: напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d). |
|
|
Из этого соотношения видно:
|
|
|
Эквипотенциальные поверхности. ЭПП – поверхности равного потенциала. Свойства ЭПП: – работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; – вектор напряженности перпендикулярен к ЭПП в каждой ее точке. |
|
|
|
|
|
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр. |
|
|
Потенциальная энергия взаимодействия зарядов. |
|
|
|
|
|
Потенциал поля точечного заряда |
|
|
|
|
|
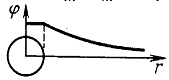
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда. |
|
|
Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными. |