Как найти путь пройденный маятником – Сайт, где вы сможете решить свои вопросы

Как найти путь, пройденный маятником?

путь маятника

Амплитуда
колебаний материальной точки составляет 30 мм, а частота 100 Гц. Определите
путь, пройденный этой точкой за 1,5 с.

Решение.

Одно
полное колебание материальная точка совершает за время, равное периоду
колебаний T = u^-1 , следовательно, за
время t она совершает N = t/T = tu колебаний.
При этом за одно колебание точка проходит путь l₁ = 4A. Значит, за время t, т.е. за N колебаний, она пройдет путь L
= 4Atu = 4•30•10^-3•1,5•100 м = 18 м.

Ответ:
L
= 18 м.

Источник: Подготовка к тестированию по физике. Шепелевич. В. Г.

Источник

Как найти путь, пройденный грузиком пружинного маятника?

Никита Багров

Ученик

(95),
закрыт

13 лет назад

Леонид Фурсов

Высший разум

(787967)

13 лет назад

Решение. x=X0*cos(((2*pi)/T)*t); t=10; T=8; Пройденный путь будет равен 5 амплитудам колебаний, т. е. 0,05*5=0,25(м) . За четверть периода пройденный путь равен 1 амплитуде. По условию задачи мы имеем 5 четвертей периода. Следовательно, пройденный путь будет равен 5*Х0=0,25(м) . Использование формулы ВАМ даст не путь, а перемещение.

Источник: физика.

Источник

Механические колебания.

Гармонические колебания.
Уравнение гармонических колебаний.
Пружинный маятник.
Математический маятник.
Свободные и вынужденные колебания.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания – это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания – это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия – это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела – это величина его наибольшего отклонения от положения равновесия.

Период колебаний $T$ – это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний $nu$ – это величина, обратная периоду: $nu =1/T$ . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

к оглавлению ▴

Гармонические колебания.

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой $x$ . Положению равновесия отвечает значение $x=0$ . Основная задача механики в данном случае состоит в нахождении функции $x(t)$ , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них – синус и косинус – являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на $pi /2$ , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

Гармонические колебания – это колебания, при которых координата зависит от времени по гармоническому закону:

$x=Acos(omega t+alpha )$ (1)

Выясним смысл входящих в эту формулу величин.

Положительная величина $A$ является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому $A$ – амплитуда колебаний.

Аргумент косинуса $omega t+alpha$ называется фазой колебаний. Величина $alpha$ , равная значению фазы при $t=0$ , называется начальной фазой. Начальная фаза отвечает начальной координате тела: $x_{0}=Acos alpha$ .

Величина называется $omega$ циклической частотой. Найдём её связь с периодом колебаний $T$ и частотой $nu$ . Одному полному колебанию отвечает приращение фазы, равное $2 pi$ радиан: $omega T=2 pi$ , откуда

$omega = frac{displaystyle 2pi }{displaystyle T}$ (2)

$omega =2 pi nu$ (3)

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):

$x=Acos(frac{displaystyle 2pi t }{displaystyle T}+ alpha), x=Acos(2 pi nu t + alpha)$ .

График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину $x_{0}$ и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае $x_{0}=A$ , поэтому можно положить $alpha=0$ . Мы получаем закон косинуса:

$x=Acos omega t$ .

График гармонических колебаний в этом случае представлен на рис. 2.

Рис. 2. Закон косинуса

Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае $x_{0}=0$ , так что можно положить $alpha =-pi /2$ . Получаем закон синуса:

$x=Asin omega t$ .

График колебаний представлен на рис. 3.

Рис. 3. Закон синуса

к оглавлению ▴

Уравнение гармонических колебаний.

Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:

$v_{x}=dot{x}=-Aomega sin(omega t+alpha )$ . (4)

Теперь дифференцируем полученное равенство (4):

$a_{x}=ddot{x}=-Aomega^{2} cos(omega t+alpha )$ . (5)

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем $-omega^{2}$ :

$a_{x}=-omega^{2}x$ . (6)

Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:

$ddot{x}+omega^{2}x=0$ . (7)

C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными $A, alpha$ ;

-никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой $omega$ и только их. Две константы $A, alpha$ определяются из начальных условий – по начальным значениям координаты и скорости.

к оглавлению ▴

Пружинный маятник.

Пружинный маятник – это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу $m$ , жёсткость пружины равна $k$ .

Координате $x=0$ отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости $vec F$ со стороны пружины. Второй закон Ньютона для груза в проекции на ось $X$ имеет вид:

$ma_{x}=F_{x}$ . (8)

Если $x>0$ (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и $F_{x}<0$ . Наоборот, если $x<0$ , то $F_{x}>0$ . Знаки $x$ и $F_{x}$ всё время противоположны, поэтому закон Гука можно записать так:

$F_{x}=-kx$

Тогда соотношение (8) принимает вид:

$ma_{x}=-kx$

или

$a_{x}=-frac{displaystyle k}{displaystyle m}x$ .

Мы получили уравнение гармонических колебаний вида (6), в котором

$omega ^{2}=frac{displaystyle k}{displaystyle m}$ .

Циклическая частота колебаний пружинного маятника, таким образом, равна:

$omega =sqrt{frac{displaystyle k}{displaystyle m}}$ . (9)

Отсюда и из соотношения $T=2 pi / omega$ находим период горизонтальных колебаний пружинного маятника:

$T=2 pi sqrt{frac{displaystyle m}{displaystyle k}}$ . (10)

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).

к оглавлению ▴

Математический маятник.

Математический маятник – это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна $l$ . Сопротивлением воздуха пренебрегаем.

Запишем для маятника второй закон Ньютона:

$m vec a=m vec g + vec T$ ,

и спроектируем его на ось $X$ :

$ma_{x}=T_{x}$ .

Если маятник занимает положение как на рисунке (т. е. $x>0$ ), то:

$T_{x}=-Tsinvarphi =-Tfrac{displaystyle x}{displaystyle l}$ .

Если же маятник находится по другую сторону от положения равновесия (т. е. $x<0$ ), то:

$T_{x}=Tsinvarphi =-Tfrac{displaystyle x}{displaystyle l}$ .

Итак, при любом положении маятника имеем:

$ma_{x}=-Tfrac{displaystyle x}{displaystyle l}$ . (11)

Когда маятник покоится в положении равновесия, выполнено равенство $T=mg$ . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство $T approx mg$ . Воспользуемся им в формуле (11):

$ma_{x}=-mgfrac{displaystyle x}{displaystyle l}$ ,

или

$a_{x}=-frac{displaystyle g}{displaystyle l}x$ .

Это – уравнение гармонических колебаний вида (6), в котором

$omega ^{2}=frac{displaystyle g}{displaystyle l}$ .

Следовательно, циклическая частота колебаний математического маятника равна:

$omega =sqrt{frac{displaystyle g}{displaystyle l}}$ . (12)

Отсюда период колебаний математического маятника:

$T=2pi sqrt{frac{displaystyle l}{displaystyle g}}$ . (13)

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

к оглавлению ▴

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).

Рис. 6. Затухающие колебания

Вынужденные колебания – это колебания, совершаемые системой под воздействием внешней силы $F(t)$ , периодически изменяющейся во времени (так называемой вынуждающей силы).

Предположим, что собственная частота колебаний системы равна $omega_{0}$ , а вынуждающая сила зависит от времени по гармоническому закону:

$F(t)=F_{0}cos omega t$ .

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
$omega$ вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.

Рис. 7. Резонанс

Мы видим, что вблизи частоты $omega=omega_{r}$ наступает резонанс – явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: $omega_{r} approx omega_{0}$ , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, $omega_{r} = omega_{0}$ , а амплитуда колебаний возрастает до бесконечности при $omega Rightarrow omega_{0}$ .

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Механические колебания.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Формулы математического маятника в физике

Формулы математического маятника

Определение и формулы математического маятника

Определение

Математический маятник – это колебательная система, являющаяся частным случаем физического маятника, вся масса которого
сосредоточена в одной точке, центре масс маятника.

Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.

Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.

Формулы математического маятника, рисунок 1

Уравнение движения математического маятника

Математический маятник – классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:

[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]

где $varphi $ – угол отклонения нити (подвеса) от положения равновесия.

Решением уравнения (1) является функция $varphi (t):$

[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]

где $alpha $ – начальная фаза колебаний; ${varphi }_0$ – амплитуда колебаний; ${omega }_0$ – циклическая частота.

Колебания гармонического осциллятора – это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.

Циклическая частота и период колебаний математического маятника

Циклическая частота математического маятника зависит только от длины его подвеса:

[ {omega }_0=sqrt{frac{g}{l}}left(3right).]

Период колебаний математического маятника ($T$) в этом случае равен:

[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]

Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.

Уравнение энергии для математического маятника

При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:

[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]

где $E_k$ – кинетическая энергия маятника; $E_p$ – потенциальная энергия маятника; $v$ – скорость движения маятника; $x$ – линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол – смещение связан с $x$ как:

[varphi =frac{x}{l}left(6right).]

Максимальное значение потенциальной энергии математического маятника равно:

[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]

Максимальная величина кинетической энергии:

[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]

где $h_m$ – максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ – максимальная скорость.

Примеры задач с решением

Пример 1

Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?

Решение. Сделаем рисунок.

Формулы математического маятника, пример 1

Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:

[frac{mv^2}{2}=mgh left(1.1right).]

Из уравнения (1.1) найдем искомую высоту:

[h=frac{v^2}{2g}.]

Ответ. $h=frac{v^2}{2g}$

Пример 2

Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}

Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:

[T=2pi sqrt{frac{l}{g}}left(2.1right).]

Выразим из нее ускорение:

[g=frac{4{pi }^2l}{T^2} .]

Проведем вычисления ускорения силы тяжести:

[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).]

Ответ. $g=9,87 frac{м}{с^2}$

Читать дальше: формулы пружинного маятника.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Механические колебания и волны

1. Механические колебания — точно или приблизительно повторяющееся движение, при котором тело смещается относительно положения равновесия, отклоняясь от него то в одну, то в другую сторону.

Для того чтобы возникли и совершались механические колебания необходима колебательная система. В механике изучаются две колебательные систем: математический и пружинный маятники.

2. Колебательная система — математический маятник — представляет собой тело, подвешенное на нити, размеры которого много меньше длины нити. Кроме того, нить математического маятника нерастяжима и не имеет массы, вся масса такого маятника сосредоточена в подвешенном к нити грузе.

В положении равновесия (рис. 59) на маятник действуют противоположно направленные сила тяжести ( vec{F}_т ) и сила упругости ( vec{F}_у ). Их равнодействующая равна нулю.

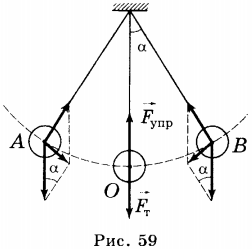
При отклонении маятника от положения равновесия вправо эти две силы направлены
под углом друг к другу, и их равнодействующая ( vec{F} ) уже не равна нулю. Под действием равнодействующей силы ( vec{F} ) маятник начнёт двигаться к положению равновесия. Поскольку груз обладает инертностью, то он пройдет положение равновесия и отклонится от него в другую сторону. Дойдя до крайнего левого положения, маятник под действием равнодействующей сил тяжести и упругости начнёт двигаться к положению равновесия. Пройдя его, он опять отклонится вправо. Процесс будет повторяться. Таким образом, в процессе колебаний изменяются смещение, скорость, действующая на него сила, ускорение маятника. При этом ускорение маятника прямо пропорционально его смещению и направлено в противоположную сторону. Для математического маятника это равенство имеет вид: ( vec{a}=-frac{vec{g}}{l} ), где ( l ) — длина нити маятника.

3. Колебательная система — пружинный маятник — это груз, прикреплённый к пружине (рис. 60). Считают, что масса пружины маятника мала по сравнению с массой груза, деформацией тела пренебрегают по сравнению с деформацией пружины. Кроме того, полагают, что деформация пружины подчиняется закону Гука ( (F=-kx) ).

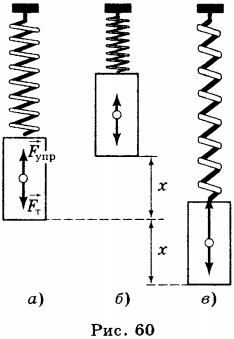
В состоянии равновесия пружина не деформирована (рис. 60), и на груз в горизонтальном направлении силы не действуют.

При выведении груза из состояния равновесия, на него будет действовать сила упругости
пружины ( vec{F}_у ), прямо пропорциональная её удлинению и направленная к положению равновесия. Под действием этой силы груз начнёт двигаться к положению равновесия.

Благодаря инертности груз пройдёт положение равновесия. Пружина сожмется, и в ней опять возникнет сила упругости. Дойдя до крайнего левого положения, груз остановится, а затем под действием силы упругости начнёт возвращаться в положение равновесия. Пройдя его, он отклонится вправо, и процесс повторится. Пружинный маятник будет совершать свободные колебания относительно положения равновесия.

Колебания, которые маятник совершает за счет однократно переданной ему энергии, называются свободными.

В соответствии со вторым законом Ньютона ( F=ma ). С другой стороны, ( F=-kx ). Откуда ( ma=-kx ), ( a=-frac{kx}{m} ). Таким образом, ускорение колебаний пружинного маятника, так же как и математического, прямо пропорционально его смещению с обратным знаком. Такие колебания называются гармоническими.

4. Отклонение маятника от положения равновесия называется смещением ( (x) ), а максимальное отклонение — амплитудой колебаний ( (A, или ,x_0) ).

Движение маятника от т. А до т. В и обратно до т. А называется полным колебанием. Время, за которое маятник совершает одно полное колебание, называется периодом колебаний (см. рис. 59). Период обозначают буквой ( T ) и измеряют в секундах.

Если маятник совершил за 4 секунды 8 полных колебаний, то его период равен 0,5 с.

Величину, обратную периоду, называют частотой колебаний. Частоту обозначают буквой ( nu ). По определению ( nu=1/T ). Единица частоты 1 герц (Гц).

Один герц — это частота таких колебаний, при которых за 1 секунду совершается одно полное колебание: 1 Гц = 1 с^-1.

Если частота колебаний 5 Гц, то это означает, что за 1 секунду совершается 5 полных колебаний. Период таких колебаний равен: ( T ) = 0,2 с.

Период колебаний математического и пружинного маятников зависит от характеристик этих систем.

Формула периода колебаний математического маятника: ( T=2pisqrt{frac{l}{g}} ), где ( l ) — длина нити маятника, ( g ) — ускорение свободного падения.

Формула периода колебаний пружинного маятника имеет вид: ( T=2pisqrt{frac{m}{k}} ), где ( m ) — масса груза, ( k ) — коэффициент жёсткости пружины.

5. Основной задачей механики является определение положения тела, т.е. его координаты, в любой момент времени. Эта задача может быть решена, если известно уравнение, выражающее зависимость координаты тела от времени. Для гармонического колебания это уравнение имеет вид: ( x=x_0!cos!omega t ) или ( x=x_0!sin!omega t ), в зависимости от того, какой была координата (смещение) маятника в начальный момент времени. В том случае, если маятник в начальный момент времени был отклонен от положения равновесия (начальная координата не равна нулю), изменение координаты происходит по закону косинуса; если он начал двигаться из положения равновесия ( (x_0=0) ), то изменение координаты (смещения) подчиняется закону синуса. В записанном уравнении координаты ( omega ) — циклическая частота колебаний. Циклическая частота колебаний равна числу колебаний за ( 2pi ) секунд: ( omega=2pisqrt{frac{2pi}{T}} ). Циклическая частота, так же как и период колебаний маятника, зависит от параметров колебательной системы: ( omega=2pisqrt{frac{g}{l}} ) и ( omega=2pisqrt{frac{k}{m}} ).

6. При выведении маятника из положения равновесия ему сообщают потенциальную энергию. За счет этой энергии происходит движение маятника к положению равновесия. В процессе движения потенциальная энергия переходит в кинетическую. В положении равновесия потенциальная энергия маятника равна нулю, а его кинетическая энергия максимальна. При движении маятника влево кинетическая энергия переходит в потенциальную; в крайнем левом положении кинетическая энергия равна нулю, а потенциальная — максимальна. В отсутствие трения полная механическая энергия маятника сохраняется.

7. При наличии сопротивления воздуха сообщенная маятнику энергия расходуется на совершение работы против силы трения, энергия маятника постоянно уменьшается, и колебания со временем прекращаются. Говорят, что они затухают.

Таким образом, реальные свободные колебания маятника всегда затухающие.

Для получения незатухающих колебаний необходимо компенсировать потери энергии. Это можно сделать, действуя на маятник с некоторой периодической силой. В этом случае колебания происходят под действием внешней силы и становятся вынужденными. Работа этой силы и восполняет потери энергии, вызванные трением. Эти колебания будут вынужденными.

Вынужденные колебания — это колебания, происходящие под действием внешней, периодически изменяющейся силы. Частота вынужденных колебаний равна частоте изменения действующей на тело силы. Частота вынужденных колебаний равна частоте изменения внешней силы.

8. Если подвесить к верёвке, прикреплённой к стойке, несколько маятников разной длины и привести в колебания один из них, то и другие маятники начнут колебаться. Частота их колебаний будет равна частоте колебаний маятника, возбудившего колебании. При этом с наибольшей амплитудой будет колебаться маятник, длина которого равна длине этого маятника. Следовательно, наибольшую амплитуду колебаний имеет маятник, собственная частота колебаний которого совпадает с частотой вынуждающей силы. Явление, которое наблюдается в этом случае, называется резонансом.

Резонанс — явление резкого возрастания амплитуды вынужденных колебаний тела, наступающего при равенстве частоты изменения внешней силы и частоты собственных колебаний тела.

Явление резонанса необходимо учитывать в практике. Известны случаи, когда вследствие резонанса разваливался на части самолёт в воздухе, ломались гребные винты у судов, рушились железнодорожные рельсы. Во всех этих случаях с резонансом приходится бороться, изменяя либо собственную частоту системы, либо частоту силы, вызывающей колебания.

9. Механической волной называется процесс распространения механических колебаний в среде.

Если закрепить конец шнура, слегка натянуть его и сместить свободный конец вверх, а затем вниз, т.е. привести его в колебания, то но шнуру «побежит» волна. Каждая точка
шнура будет совершать вынужденные колебания с частотой внешней силы, но с некоторым опозданием. При распространении колебаний по шнуру волна «бежит» в горизонтальном направлении, а колебания частицы совершают в вертикальном направлении.

Волны, направление распространения которых перпендикулярно направлению колебаний частиц среды, называются поперечными.

Поперечные волны представляют собой чередование горбов и впадин (рис. 61).

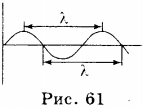
Расстояние между двумя ближайшими горбами или впадинами называется длиной волны.

Длина волны обозначается букой ( lambda ) и измеряется в метрах.

На расстояние, равное длине волны, волна распространяется за время, равное периоду колебаний.

10. Если закрепить один конец длинной пружины, а по другому ударить, то возникшее на конце пружины сгущение витков «побежит» по ней (рис. 62). В этом случае волна представляет собой распространение сгущений и разрежений. Частицы среды при этом совершают колебания вдоль направления распространения волны. Такие волны называют продольными.

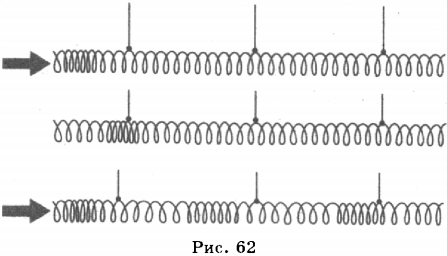
Продольные волны — это такие, направление распространения которых совпадает с направлением колебаний частиц среды.

11. Волновое движение имеет следующие особенности:

механические волны образуются благодаря инертности частиц среды и взаимодействию между ними, проявляющемуся в существовании сил упругости;
каждая частица среды совершает вынужденные колебания такие же, что и первая частица, приведенная в колебания, частота которых равна частоте внешней силы. Период колебаний всех частиц одинаков;
колебание каждой частицы происходит с запаздыванием, которое обусловлено её инертностью. Это запаздывание тем больше, чем дальше находится частица от источника колебаний;
вместе с волной не переносится вещество, переносится энергия.

12. Распространение продольных волн связано с изменением объёма тела. Они могут распространяться как в твёрдых, так и в жидких и газообразных телах, поскольку во всех этих телах при изменении объёма возникают силы упругости.

Распространение поперечных волн связано главным образом с изменением формы тела. В газах и жидкостях при изменении формы силы упругости не возникают, поэтому поперечные волны в них распространяться не могут. Поперечные волны распространяются только в твёрдых телах.

Примером волнового движения в твёрдом теле является распространение колебаний во время землетрясений. От центра землетрясения распространяются как продольные, так и поперечные волны. Сейсмическая станция принимает сначала продольные волны, а затем поперечные, т.к. скорость последних меньше. Если известны скорости поперечной и продольной волн и измерен промежуток времени между их приходом, то можно определить расстояние от центра землетрясения до станции.

13. Скоростью волны считается скорость перемещения гребня или впадины в поперечной волне, сгущения или разрежения в продольной волне.

За время, равное периоду колебаний ( (T) ), гребень или впадина перемещаются на расстояние, равное длине волны ( (lambda) ). Следовательно, скорость волны ( (v) ) равна: ( v=frac{lambda}{T} ).

Поскольку ( T=frac{1}{v} ), то формулу для скорости можно записать иначе: ( v=lambda nu ).

Скорость волны равна произведению длины волны и частоты колебаний.

14. Колебания, происходящие с частотой от 16 Гц до 20 000 Гц, являются звуковыми колебаниями. Для распространения звуковых колебаний, так же как и любых механических колебаний, необходима упругая среда.

Скорость звука можно определить, если известны расстояние от источника звука ( S ) и время распространения звука ( t ): ( v=frac{S}{t} ). Скорость звука неодинакова в разных средах и зависит от температуры среды.

Физиологическим характеристикам звука (громкости, высоте тона) соответствуют физические характеристики. Громкость звука определяется амплитудой колебаний. Чем она больше, тем громче звук. Звук тем выше, чем больше частота колебаний.

Содержание

ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
Ответы

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Какой путь пройдёт груз математического маятника за 10 полных колебаний, если амплитуда колебаний равна 3 см?

1) 30 см
2) 60 см
3) 90 см
4) 120 см

2. Маятник совершает 20 полных колебаний за 10 с. Чему равна частота колебаний маятника?

1) 20 Гц
2) 2 Гц
3) 1 Гц
4) 0,5 Гц

3. Во сколько раз надо изменить массу груза пружинного маятника, чтобы период колебаний увеличился в 9 раз?

1) увеличить в 3 раза
2) уменьшить в 9 раз
3) уменьшить в 81 раз
4) увеличить в 81 раз

4. Массу груза математического маятника, совершающего гармонические колебания, увеличили в 9 раз. При этом период колебаний

1) увеличился в 3 раза
2) увеличился в 9 раз
3) уменьшился в 3 раза
4) не изменился

5. Если перенести математический маятник с Земли на Марс, то

1) частота колебаний не изменится
2) частота колебаний увеличится
3) частота колебаний уменьшится
4) маятник не будет колебаться

6. На рисунке представлен график колебаний математического маятника. Период колебаний маятника равен

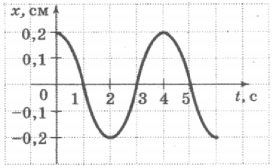
1) 1 с
2) 2 с
3) 3 с
4) 4 с

7. Период колебаний частиц в волне можно вычислить по формуле

1) ( T=frac{nu}{lambda} )
2) ( T=frac{lambda}{nu} )
3) ( T=lambdanu )
4) ( T=vnu )

8. На рисунке показан график волны, бегущей вдоль упругого шнура, в некоторый момент времени. Длина волны равна расстоянию

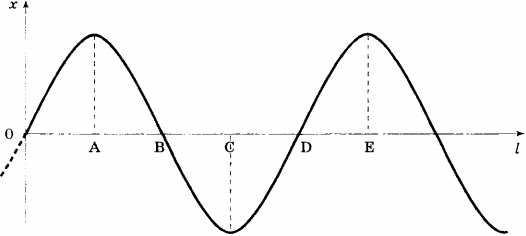
1) ВС
2) BD
3) BE
4) OD

9. Сравните громкость звука и высоту тона двух звуковых колебаний, если для первого колебания: амплитуда ( A_1 ) = 2 мм, частота ( nu_1 ) = 500 Гц, для второго колебания: ( A_2 ) = 4 мм, частота ( nu_w ) = 300 Гц.

1) громкость первого звука больше, чем второго, а высота тона меньше
2) и громкость, и высота тона первого звука больше, чем второго
3) и громкость и высота тона первого звука, меньше, чем второго
4) громкость первого звука меньше, чем второго, а высота тона больше

10. Волна частотой 3 Гц распространяется в среде со скоростью 6 м/с. Длина волны равна

1) 18 м
2) 2 м
3) 1 м
4) 0,5 м

11. Математический маятник отвели в сторону и отпустили. Как будут изменяться значения величин, характеризующих колебания маятника при его движении к положению равновесия. Для каждой величины из первого столбца подберите соответствующее характеру её изменения слово из второго столбца. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры могут повторяться.

ВЕЛИЧИНЫ
A) смещение
Б) скорость
B) потенциальная энергия

ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличивается
2) уменьшается
3) не изменяется

12. Среди приведённых ниже положений укажите два правильных и запишите их номера в таблице.

1) Звук распространяется только в воздухе.
2) Колебания, частота которых больше 20 000 Гц, называются ультразвуком.
3) Инфразвук — колебания, частота которых больше 16 Гц.
4) Эхо — явление многократного отражения звуковых волн от преград.
5) Звуковые волны — поперечные.

Часть 2

13. Мимо рыбака, сидящего на пристани, прошло 5 гребней волны за 10 с. Каков период колебаний поплавка на волнах?

Ответы

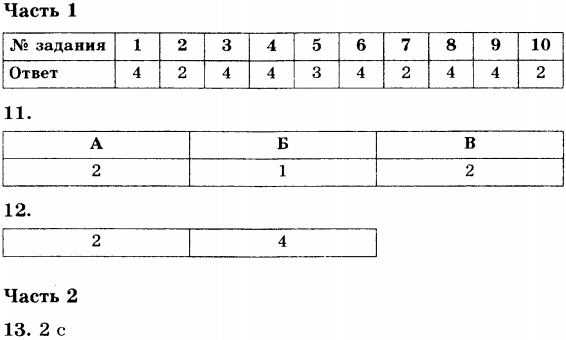
Механические колебания и волны

3.3 (65.64%) 39 votes

Источник