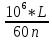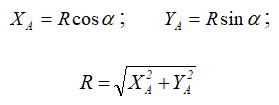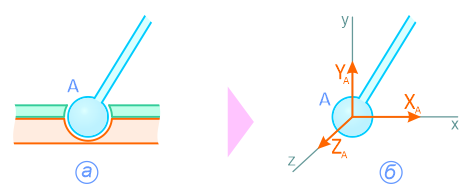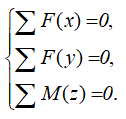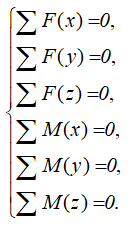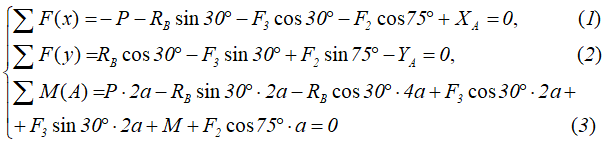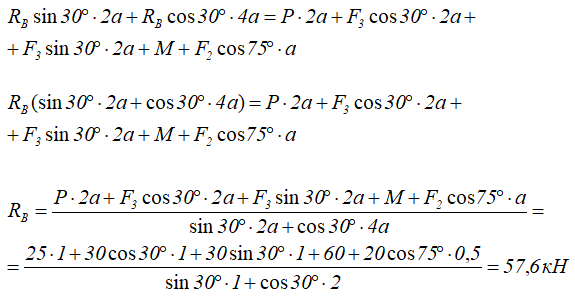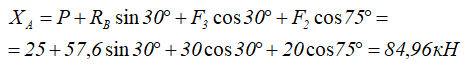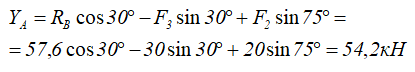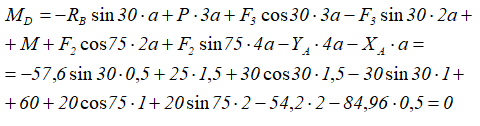Как найти реакцию опоры подшипников

Решение выполняется в два этапа:

1.Определение
реакций в опорах предварительно выбранных
подшипни­ков: по
результатам первого этапа проводится
проверочный расчет подшипни­ков.

2.Определение
реакций в опорах окончательно принятых
подшипников, построение эпюр изгибающих
и крутящих моментов и составление схемы
нагру­жения подшипников; второй
этап выполняется при проверочном расчете
валов на прочность.

Расчет
выполняется в следующей последовательности:

• вычерчивается
  расчетная схема вала в соответствии с
  выполненной схе­мой нагружения валов
  редуктора;

• выписываем
  исходные данные для расчета: силы в
  зацеплении редуктор- ной пары (F_t,F_r,
  F_a)
  и консольные силы гибкой передачи ^,_п
  и муфты Fm

• расставляем
  расстояния между точками приложения
  реакций в опорах подшипников и консольной
  силы;

• определяем
  реакции в опорах предварительно
  выбранных подшипников вала в вертикальной
  и горизонтальной плоскости, составив
  два уравнения равно­весия плоской
  системы сил;

• определяем
  суммарные радиальные реакции опор
  подшипников, напри­мер, R_a
  = J^fy,
  Н, где R_Ax
  и R_Ay
  – соответственно реакции в опоре
  под­шипника А в горизонтальной и
  вертикальной плоскости;

Расчеты
в вертикальной плоскости:

• определяем
  реакции в опорах окончательно принятых
  подшипников, со­ставив два уравнения
  равновесия плоской системы сил;

• определяем
  значения изгибающих моментов по
  участкам, составив урав­нения
  изгибающих моментов;

• строим
  в масштабе эпюру изгибающих моментов
  и указываем макси­мальный момент;

Выполняем
расчеты в горизонтальной плоскости
аналогично расчетам в вертикальной
плоскости.

• определяем
  крутящий
  момент на валу и строим в масштабе его
  эпюру. Знак эпюры определяется
  направлением момента от окружной силы
  F_t,
  если смотреть со стороны выходного
  конца вала.

• определяем
  суммарные реакции опор подшипников
  вала.

• определяем
  суммарные изгибающие моменты в наиболее
  нагруженных

сечениях
вала М_су„
= I
MJ
+ MJ,
Н-м, где М_х
и М_у
– соответственно изгибающиемоменты
в горизонтальной и вертикальной
плоскости.составляем
схему нагружения подшипников.

9 Проверка долговечности подшипников

Конструкция
подшипникового узла должна обеспечивать
фиксацию валов

в осевом
направлении, компенсацию температурных
деформаций, надежную

смазку и
защиту подшипников от посторонних
частиц, удобство монтажа, демонтажа и
регулировки.

Выбор
типоразмера подшипника зависит от
характера нагрузки, ее вели-

чины и
направления, частоты вращения и условий
эксплуатации.

Проектируют
подшипниковые узлы в такой последовательности:

1. Выполняют
эскизную компоновку узла; на основании
расчетной схемы

намечают
расстояние между опорами и закрепленными
на валу деталями.

2. На
основании кинематической схемы и силовой
характеристики меха-

низма
определяют величины и направления
нагрузок на опоры.

3. Намечают
тип подшипника с учетом нагрузок,
конструкции узла, усло-

вий эксплуатации
и монтажа.

4. Определяют
эквивалентную нагрузку и проверяют
расчетную долговеч-

ность
подшипника.

5. Назначают
посадки на внутренние и наружные кольца
подшипника и

выбирают
способ крепления колец на посадочных
местах.

6. Определяют
систему смазки и конструкцию уплотнения.

7.
Окончательно оформляют конструкцию
подшипникового узла.

При выборе
подшипников следует руководствоваться
не только конструк-

тивными, но
и экономическими соображениями; например,
учитывать, что шари-

ковые
подшипники дешевле роликовых, подшипники
повышенных классов точ-

ности
значительно дороже подшипников
нормального класса.

В опорах,
подверженных действию ударных нагрузок,
предпочтение сле-

дует отдавать
роликоподшипникам. При действии на узел
только радиальных на-

грузок
следует, как правило, ставить
шарикоподшипники.

Для
подшипников с частотой вращения кольца
n < 1 мин-1 основной харак-

теристикой
служит статическая грузоподъемность
Со; при большей частоте вра-

щения –
динамическая грузоподъемность С.

По ГОСТ
18855-73 динамической грузоподъемностью
радиальных и ради-

ально-упорных
подшипников называют величину постоянной
радиальной нагрузки, которую группа
идентичных подшипников с неподвижным
наружным кольцом может выдержать в
течение 1 млн. оборотов внутреннего
кольца. Для упорных подшипников
динамическая грузоподъемность — это
постоянная центральная осевая нагрузка,
которую любой из группы идентичных
подшипников сможет выдерживать в течение
1 млн. оборотов одного из колец подшипника.
Под номинальной долговечностью понимают
срок службы подшипников, в течение
которого неменее 90% из данной группы
при одинаковых условиях должны проработать
безпоявления признаков усталости
металла.

Расчетную
долговечность L в млн. оборотов L_hили в часах определяют по

динамической
грузоподъемности С и величине эквивалентной
нагрузки Рэ

где L –
долговечность подшипника, млн. об;

а1 –
коэффициент надежности;

а₂₃– обобщенный коэффициент совместного
влияния качества металла и ус-

ловий
эксплуатации подшипника;

С –
динамическая грузоподъемность, Н;

Рэ –
эквивалентная динамическая нагрузка,
Н;

m – показатель
степени, для шариковых радиальных
подшипников, m =3, для

роликоподшипников
m =3,33.

Для любых
подшипников

L_h=

где Lh –
базовая долговечность, ч;

~ 174 ~

L –
долговечность подшипника, млн. об;

n – частота
вращения подшипника, мин-1.

Требуемая
долговечность подшипника предусмотрена
ГОСТ 16162-85 и

составляет:
для червячных редукторов не менее 5000ч,
а для зубчатых – не менее

10000ч.

Эквивалентная
нагрузка в зависимости от вращения
колец, радиальной и

осевой
нагрузки определяется для радиальных
шарикоподшипников и радиально-

упорных
шарико – и роликоподшипников

P_э=(XVF_r+YF_a)K_σK_T

Для упорных
шариковых и роликовых подшипников

Pэ=FaKσKт

где – коэффициент
радиальной нагрузки (таблицы 10.2 – 10.3);

– коэффициент
осевой нагрузки (таблицы 10.1 – 10.2);

– коэффициент,
учитывающий вращение колец; при вращении
внутреннего

кольца ,
наружного кольца ;

– радиальная
нагрузка, Н;

– осевая
нагрузка, Н;

– температурный
коэффициент (таблица 10.1);

– коэффициент
безопасности (таблица 10.4)__

Определение сил, нагружающих подшипники

Определение радиальных реакций. Вал на подшипниках, установленных по одному в опоре, условно рассматривают как балку на шарнирно-подвижных опорах или как балку с одной шарнирно-подвижной и од­ной шарнирно-неподвижной опорой. Ради­альную реакцию Fr подшипника считают приложенной к оси вала в точке пересече­ния с ней нормалей, проведенных через середины контактных площадок. Для ради­альных подшипников эта точка расположе­на на середине ширины подшипника. Для радиально-упорных подшипников расстояние а между этой точкой и торцом подшипника может быть определено графиче­ски (рис. 25) или аналитически:

подшипники шариковые радиально-упорные однорядные

а = 0,5[B + 0,5(d + D)tga];

подшипники роликовые конические однорядные

а = 0,5[Т + (d + D)е / 3].

Ширину В кольца, монтажную высоту Т коэффициент е осевого нагружения, угол а контакта, а также диаметры d и D при­нимают по каталогу.

Рис.25.Расположение точки приложения радиальной реакции в радиально-упорных подшипниках

Реакции опор определяют из уравнения равновесия: сумма моментов внешних сил относительно рассматриваемой опоры и момента реакции в другой опоре равна ну­лю.

В ряде случаев направление вращения может быть переменным или неопределен­ным, причем изменение направления вра­щения может привести к изменению не только направления, но и значений реак­ций опор. При установке на концы валов соединительных муфт направление силы на вал от муфты неизвестно. В таких случаях при расчете реакций рассматривают наибо­лее опасный вариант. Возможная ошибка при этом приводит к повышению надежно­сти.

Определение осевых реакций. При уста­новке вала на двух радиальных шариковых или радиально-упорных подшипниках не­регулируемых типов осевая сила Fa, нагру­жающая подшипник, равна внешней осевой силе F_A, действующей на вал. Силу F_A вос­принимает тот подшипник, который огра­ничивает осевое перемещение вала под действием этой силы.

При определении осевых сил, нагру­жающих радиально-упорные подшипники регулируемых типов, следует учитывать осевые силы, возникающие под действием радиальной нагрузки Fr вследствие наклона контактных линий. Значения этих сил за­висят от типа подшипника, угла контакта, значений радиальных сил, а также от того, как отрегулированы подшипники (см. рис 22, а-в). Если подшипники собраны с большим зазором, то всю нагрузку воспри­нимает только один или два шарика или ролика (рис. 22, а). Осевая составляющая нагрузки при передаче ее одним телом ка­чения равна F_rtga. Условия работы под­шипников при таких больших зазорах не­благоприятны, и поэтому такие зазоры не­допустимы. Обычно подшипники регули­руют так, чтобы осевой зазор при устано­вившемся температурном режиме был бы близок к нулю. В этом случае под действи­ем радиальной нагрузки Fr находятся около половины тел качения (рис. 22, б), а сум­марная по всем нагруженным телам каче­ния осевая составляющая из-за наклона контактных линий равна е’ Fr и представля­ет собой минимальную осевую силу, кото­рая должна действовать на радиально-упорный подшипник при заданной ради­альной силе:

Fa min = е′ Fr. (24)

Для шариковых радиально-упорных под­шипников с углом контакта а < 18° Famin = e’Fr , где е’ — коэффициент мини­мальной осевой нагрузки. В подшипниках такого типа действительный угол контакта отличается от начального и зависит от ра­диальной нагрузки Fr и базовой статиче­ской грузоподъемности Соr. Поэтому коэф­фициент е’ определяют по формулам:

для подшипников с углом контакта а = 12°

е′ = 0,563(Fr / Cor)^0,195; (25)

для подшипников с углом контакта а = 15°

е′ = 0,579(Fr / Cor)^0,136 (26)

Для шариковых радиально-упорных под­шипников с углом контакта а ≥ 18° е′ = е и Famin = eFr . Значения коэффициента еосевого нагружения принимают по табл. 64.

Для конических роликовых.е’ = 0,83е и Famin = 0,83 е Fr. Значения коэффициента е принимают по каталогу.

Под действием силы Faminнаружное кольцо подшипника поджато к крышке корпуса. При отсутствии упора кольца в крышку оно будет отжато в осевом направ­лении, что приведет к нарушению нормальной работы подшипника. Для обеспечения нормальных условий работы oceвая сила, нагружающая подшипник, должна быть не меньше минимальной: Fa > Famin.

Это условие должно быть выполнено для каждой опоры.

Если Fa≥ Famin, то более половины или все тела качения подшипника находятся под нагрузкой (см. рис. 22, в). Жесткость опоры с ростом осевой нагрузки увеличивается, поэтому в некоторых опорах, например в опорах шпинделей станков, применяют сборку с предварительным натягом. Для нормальной работы радиально-упорных подшипников необходимо, в каждой опоре осевая сила, нагружающий подшипник, была бы не меньше минимальной:

F_a1 ≥ F_{a1 min}и F_a2 ≥ F_{a2 min}

Кроме того, должно быть выполнено условие равновесия вала — равенство нуля суммы всех осевых сил, действующих на вал. Например, для схемы по рис. 26 имеем:

F_A + F_a1 – F_a2 = 0

Пример нахождения осевых peaкций опор. В представленной на рис. 26 расчетной схеме обозначены: F_Aи F_R — внешние осевая и радиальная нагрузки, действующие на вал; F_r1 и F_r2 — радиальные peaкции опор; F_a1 и F_a2 — осевые реакции опор.

Решение может быть найдено при совместном удовлетворении трех уравнений:

— из условия Fa≥ Famin в каждой oпоре с учетом (24) следует:

F_a1 ≥ e₁′ F_r1, F_a2 ≥ e₁′ F_r2

— из условия равновесия вала под действием осевых сил следует:

Рис. 26. Схема нагружения вала и опор с радиально-упорными регулируемыми подшипниками

Для нахождения решения применяют метод попыток, предварительно осевую силу в одной из опор принимая равной минимальной.

1. Пусть, например, F_a1 = e₁′ F_r1 .

Тогда из условия равновесия вала имеем

F_a2 = F_A + F_a1 = F_A + e′F_r1.

Проверяем выполнение условия Fa > Faminдля второй опоры. Если при этом F_a2 ≥ e₂‘ F_r2 — то осевые силы найдены правильно. Если F_a2 < е₂′ F_r2 (что недопус­тимо), то нужно предпринять вторую попытку.

2. Следует принять: F_a2 = е₂′ F_r2 . Тогда из условия равновесия вала имеем

F_a1 = F_a2 — F_A = e₂‘ F_r2 — F_A.

При этом условие F_a1 ≥ e₁′ F_r1 будет обя­зательно выполнено.

Подбор подшипников

Основной критерий работоспособности и порядок подбора подшипников зависит от значения частоты вращения кольца. Подшипники выбирают по статической грузоподъемности, если они воспринимают внешнюю нагрузку в неподвижном состоя­нии или при медленном вращении (n≤ 10об/мин). Подшипники, работающие при n > 10об/мин, выбирают по динамиче­ской грузоподъемности, рассчитывая их ресурс при требуемой надежности. Под­шипники, работающие при частоте враще­ния n > 10об/мин и резко переменной нагрузке, также следует проверять на ста­тическую грузоподъемность.

Предварительно назначают тип и схему Установки подшипников (см. выше). Подбор подшипников выполняют для обе­их опор вала. В некоторых изделиях, например в редукторах, для обеих опор применяют подшипники одного типа и одного размера. Тогда подбор выполняют по наиболее нагруженной опоре. Иногда из соотношения радиальных и осевых сил нельзя заранее с уверенностью сказать, какая опора более нагружена. Тогда расчет ведут параллельно для обеих опор до получения значений эквивалентных нагрузок, по которым и определяют более нагруженную опору.

Расчет подшипников на статическую грузоподъемность

Значения базовой статической грузо­подъемности для каждого подшипника за­ранее подсчитаны по формулам (1)-(4) и указаны в каталоге.

При расчете на статическую грузоподъ­емность проверяют, не будет ли статиче­ская эквивалентная нагрузка на подшипник превосходить статическую грузоподъем­ность, указанную в каталоге:

Роr≤ Соrили Poa≤ Coa

При выборе и расчете подшипников следует иметь в виду, что допустимая ста­тическая эквивалентная нагрузка Ро может быть меньше, равна или больше базовой статической грузоподъемности. Значение этой нагрузки зависит от требований к плавности хода, малошумности и к момен­ту трения, а также и от действительной геометрии поверхностей контакта. Чем вы­ше перечисленные требования, тем меньше значение допустимой статической эквива­лентной нагрузки.

Если не требуется высокая плавность хода, то возможно кратковременное повы­шение Por(Poa) до 2Cor(2Coa). При повы­шенных требованиях к плавности хода, малошумности и к стабильности момента трения рекомендуют уменьшить допускае­мую статическую эквивалентную нагрузку Pоr(Pоа) до Cоr/ S₀ (Соa/ S₀). Коэффици­ент запаса S₀ = 1,5 для упорных подшипни­ков крановых крюков и подвесов; S₀ = 2 для приборных прецизионных поворотных устройств; S₀ = 4 для ответственных тяжелонагруженных опор и поворотных кругов.

Пример. Проверить пригодность под­шипника 210 для следующих условий рабо­ты: вращение медленное (до 1об/мин) эпи­зодическое при действии нагрузки с со­ставляющими: радиальной Fr = 9000Н и осевой Fo = 1600Н; требования к мало­шумности и плавности хода — высокие.

Решение. Базовая статическая радиаль­ная грузоподъемность подшипника 210 по каталогу Соr= 19800Н. Для шарикового радиального однорядного подшипника в соответствии с табл. 59 X₀ = 0,6 и Y₀ = 0,5. Подставив в (5) и (6), получим

Por = X₀Fr + Y₀Fa = 0,6 · 9000 + 0,5 · 1600 = 6200H;

Por= Fr = 9000H.

Принимаем наибольшее значение Por= 9000H. Для шариковых подшипников с высокими требованиями к малошумности и плавности хода можно принять S₀ = 2. Для таких условий работы должно выпол­няться соотношение Роr≤ Соr / S₀. После подстановки получим:

9000 < 19800/2 = 9900.

Следовательно, для данных условий ра­боты подшипник 210 пригоден.

Расчет подшипников на заданный ресурс

Исходные данные:F_r1, F_r2 — ра­диальная нагрузка (радиальная реакция) каждой опоры двухопорного вала, Н: Fa -внешняя осевая сила, действующая на вал, Н; n- частота вращения кольца (как пра­вило, частота вращения вала), об/мин; d — диаметр посадочной поверхности вала, ко­торый берут из компоновочной схемы, мм; L’sa, L’sah — требуемый ресурс при необхо­димой вероятности безотказной работы подшипника соответственно в млн. об.или в ч; режим нагружения; условия эксплуата­ции подшипникового узла (возможная пе­регрузка, рабочая температура и др.).

Условия работы подшипников весьма разнообразны и могут различаться по вели­чине кратковременных перегрузок, рабочей температуре, вращению внутреннего или наружного кольца и др. Влияние этих фак­торов на работоспособность подшипников учитывают введением в расчет эквивалент­ной динамической нагрузки (19) — (22) до­полнительных коэффициентов.

Подбор подшипников качения выполня­ют в такой последовательности.

1. Предварительно назначают тип и схему установки подшипников.

2. Для назначенного подшипника из ка­талога выписывают следующие данные:

— для шариковых радиальных и радиально-упорных с углом контакта а < 18° значения базовых динамической Сr и ста­тической Соr радиальных грузоподъемностей;

— для шариковых радиально-упорных углом контакта а ≥ 18° значение Сr, а из табл. 64 значения коэффициентов X радиальной, Y осевой нагрузок, коэффициента осевого нагружения:

— для конических роликовых значений Сr, Y и е, а также принимают X = 0,4 (табл. 66).

3. Из условия равновесия вала и условия ограничения минимального ypoвня осевых нагрузок на радиально-упорные подшипники определяют осевые силы F_a1, F_a2.

4. Для подшипников шариковых радиальных, а также шариковых радиально-упорных с углом контакта а < 18° по табл. 64 в соответствии с имеющейся информацией находят значения X, Yи е в зависимости от

f₀Fa / CorилиFa / (i z D_w²).

5. Сравнивают отношение Fa/(VFr) с коэффициентом е и окончательно принимают значения коэффициентов X и Y: при Fa/(VFr)≤eпринимают X = 1 и Y=0, при Fa/(VFr)>eдля подшипников шариковых радиальных и радиально-упорных окончательно принимают записанные ранее (в п.1 и 4) значения коэффициентов X и Y.

Здесь V — коэффициент вращения кольца: V = 1 при вращении внутреннего кольца подшипника относительно направления радиальной нагрузки и V= 1, 2 при вpaщении наружного кольца.

Для двухрядных конических роликовых подшипников значения X, Y и е – по табл. 66.

6. Вычисляют эквивалентную динамическую нагрузку:

— радиальную для шариковых радиальных и шариковых или роликовых радиально-упорных

Рr = (VXFr + YFa) K_БK_T; (27)

— радиальную для роликовых радиальных подшипников:

Pr =Fr V К_БК_Т; (28)

— осевую для шариковых и роликовых упорных подшипников:

Pа = Fа К_БК_Т (29)

— осевую для шариковых и роликовых упорно-радиальных подшипников

Pa = (XFr+ YFa) K_БK_T. (30)

Значение коэффициента К_Б безопасно­сти принимают по табл. 69, а температур­ного коэффициента К_Т — в зависимости от рабочей температуры t_раб подшипника:

69. Рекомендуемые значения коэффициентов безопасности

Для работы при повышенных температурах применяют подшипники со специальной стабилизирующей термообработкой изготовленные из теплостойких сталей. Для подшипников, работающих при переменных режимах нагружения, задаваемых циклограммой нагрузок и соответствующими этим нагрузкам частотами вращения (рис. 27), вычисляют эквивалентную динамическую нагрузку при переменном режи­ме нагружения

где Рi и Li — постоянная эквивалентная на­грузка (радиальная или осевая) на i-м ре­жиме и продолжительность ее действия в млн. об. Если Li задана в ч-Lhi, то ее пере­считывают на млн. об.с учетом частоты вращения n_i, об/мин:

Если нагрузка на подшипник изменяется по линейному закону от Рminдо Рmax, то эквивалентная динамическая нагрузка

Рис. 27.Аппроксимация нагрузок и частот вращения

Известно, что режимы работы машин с переменной нагрузкой сведены к шести типовым режимам нагружения (см. ГОСТ 21354-87. Передачи зубчатые цилиндриче­ские эвольвентные внешнего зацепления. Расчет на прочность): 0 — постоянному; I -тяжелому; II — среднему равновероятному; III- среднему нормальному; IV — легкому; V — особо легкому.

Для подшипников опор валов зубчатых передач, работающих при типовых режимах нагружения, расчеты удобно вести с помо­щью коэффициента эквивалентности К_E:

При этом по известным максимальным, длительно действующим силам F_r1max, F_{r2 max}, F_Amax(соответствующим максимальному из длительно действующих вра­щающему моменту) находят эквивалентные нагрузки [3]:

по которым в соответствии с пп. 2-6 ведут расчет подшипников, как при постоянной нагрузке.

7. Определяют скорректированный по уровню надежности и условиям примене­ния расчетный ресурс подшипника, ч:

где С — базовая динамическая грузоподъем­ность подшипника (радиальная Сr или осевая Са), Н; Р — эквивалентная динамическая нагрузка (радиальная Рr или осевая, а при переменном режиме нагружения или Р_Еа), Н; k — показатель степени: k для шариковых и k = 10/3 для роликовых подшипников; n — частота вращения кольца, об/мин; а₁ — коэффициент, корректирующий ресурс в зависимости от необходимой надежности (табл. 68); а₂₃ — коэффициент, характеризующий совместное влияние на ресурс особых свойств подшипника и условий его эксплуатации (табл. 70).

Базовый расчетный ресурс подтверждают результатами испытаний подшипника на специальных машинах и в определенных условиях, характеризуемых наличием гидродинамической пленки масла между контактирующими поверхностями колец и отсутствием повышенных перекосов колец подшипника. В реальных условиях эксплуатации возможны отклонения от этих условий, что приближенно и oценивают коэффициентом а₂₃.

При выборе коэффициента а₂₃ различают следующие условия применения подшипника:

1 — обычные (материал обычной плавкой, наличие перекосов колец, отсутствие надежной гидродинамической пленки масла, наличие в нем инородных частиц);

2 — характеризующиеся наличием упругой гидродинамической пленки масла в контакте колец и тел качения (параметр Δ ≥ 2,5); отсутствие повышенных перекосов в узле; сталь обычного изготовления;

3 — то же, что в п.2, но кольца и тела качения изготовлены изстали электрошлакового или вакуумно-дугового переплава.

70. Рекомендуемые значения коэффициента

71. Рекомендуемые значения расчетных ресурсов для машин и оборудования

Здесь Δ — параметр режима смазки — ха­рактеризует гидродинамический режим смазки подшипника (относительную толщину смазочной пленки). Расчет Δ приве­ди, например, в [1, 2].

Формулы расчета ресурса справедливы при частотах вращения свыше 10об/мин до предельных по каталогу, а также если Pr (или Pa), а при переменных нагрузках Рrmax(или Pamax) не превышают 0,5Сr (или 0,5Ca).

8. Оценивают пригодность намеченного размера подшипника. Подшипник пригоден, если расчетный ресурс больше или равен требуемому:

Lsah≥ Lsah′.

В некоторых случаях в одной опоре ус­танавливают два одинаковых радиальных или радиально-упорных однорядных под­шипника, образующих один подшипнико­вый узел. При этом пару подшипников рассматривают как один двухрядный под­шипник. При определении ресурса по формуле п. 7 вместо Сr подставляют базо­вую динамическую радиальную грузоподъемность С_rсум комплекта из двух подшип­ников: для шарикоподшипников С_rсум = 1,625 Сr, для роликоподшипников С_rсум = 1,714Сr. Базовая статическая ради­альная грузоподъемность такого комплекта равна удвоенной номинальной грузоподъ­емности одного однорядного подшипника C_0rcум = 2С_0r.

При определении эквивалентной на­грузки Рr значения коэффициентов X и Y принимают как для двухрядных подшипни­ков: для шарикоподшипников по табл. 64; для роликоподшипников — по табл. 66.

Рекомендуемые значения ресурсов под­шипников различных машин приведены в табл. 71.

Пример 1. Подобрать подшипники ка­чения для опор выходного вала цилиндри­ческого зубчатого редуктора (рис. 28). Час­тота вращения вала n = 120об/мин. Тре­буемый ресурс при вероятности безотказной работы 90%: L_10ah′ = 25000ч. Диаметр посадочных поверхностей вала d = 60мм. Максимальные, длительно действующие силы: F_r1max=6400Н, F_r2mах = 6400Н, F_Amax= 2900H. Режим нагружения — II(средний равновероятный). Возможны кратковременные перегрузки до 150% но­минальной нагрузки. Условия применения подшипников — обычные. Ожидаемая тем­пература работы t_pаб = 50°С.

Решение. 1. Для переменного типового режима нагруженияII коэффициент экви­валентности К_E = 0,63 (см. п.6).

Вычисляем эквивалентные нагрузки, приводя переменный режим нагружения к эквивалентному постоянному:

F_r1 = K_EF_{r1 max} = 0,63 · 6400 = 4032Н;

Рис. 28. Расчетная схема к примеру 1

F_r2 = K_EF_r2max = 0,63 · 6400 = 4032Н;

F_A = K_EF_Amax = 0,63 · 2900 = 1827Н.

2. Предварительно назначаем шариковые радиальные подшипники легкой ceрии 212. Схема установки подшипников: 2а (см. рис. 24) — обе опоры фиксирующие; каждая фиксирует вал в одном направлении.

3. Для принятых подшипников по каталогу находим: Сr — 52000Н, Соr = 31000H, d = 60мм, D = 110мм, Dw= 15,88мм.

4. Для радиальных шарикоподшипников из условия равновесия вала следует F_a1 = F_A= 1827Н, F_a2 = 0. Дальнейший расчет выполняем для более нагруженного подшипника опоры 1.

5. По табл. 58 для отношений D_wcosа / Dpw = 15,88cos0° / 85 = 0,19 находим значение f₀ = 14,2; здесь Dpw= 0,5(d + D) = 0,5(60 + 110) = 85мм. Далее по табл. 64 определяем значение коэффициента е для отношения f₀F_a1 / Соr = 14,2 × 1827 / 31000 = 0,837 : е = 0,27.

6. Отношение Fa / Fr = 1827 / 4032 = 0,45, что больше е = 0,27. По табл. 64 для отношения f₀F_a1 / Cor = 0,837 принимаем Х = 0,56, Y= 1,64.

7. Эквивалентная динамическая радиальная нагрузка по формуле (27) при V = 1 (вращение внутреннего кольца); К_Б = 1,4 (см. табл. 69); К_Т = 1 (t_раб < 100°С)

Рr = (1 · 0,56 · 4032 + 1,64 · 1827) 1,4 · 1 = 7356Н.

8. Расчетный скорректированный ресурс подшипника по формуле (31) при а₁= 1 (вероятность безотказной работы 90%, табл. 68), а₂₃ = 0,7 (обычные условия применения, табл. 70), k = 3 (шариковый подшипник)

9. Так как расчетный ресурс больше требуемого: L_10ah > L_10ah′ (34344 > 25000), то предварительно назначенный подшипник 212 пригоден. При требуемом ресурсе надежность выше 90%.

Пример 2. Подобрать подшипники для опор вала редуктора привода цепного кон­вейера (рис. 29). Частота вращения вала n = 200об/мин. Требуемый ресурс при вероятности безотказной работы 90%:

L_10ah′ = 20000ч. Диаметр посадочных поверхностей вала d = 45мм. Максимальные, длительно действующие силы: F_r1max= 9820Н, F_r2max = 8040Н, F_Amax= 3210Н. Режим нагружения — III (средний нормальный). Возможны кратковременные перегрузки до 150% номинальной нагрузки. Условия применения подшипников обычные. Ожидаемая температура работы t_раб = 45°С.

Решение. 1. Для переменного типового режима нагруженияIII коэффициент экви­валентности К_E= 0,56 (см. п.6).

Вычисляем эквивалентные нагрузки, при­водя переменный режим нагружения к экви­валентному постоянному:

2. Предварительно назначаем кониче­ские роликовые подшипники легкой серии — 7209А. Схема установки подшипников: 2а (см. рис. 24) — обе опоры фиксирующие: каждая фиксирует вал в одном направле­нии.

3. Для принятых подшипников из ката­лога находим: Сr = 62700Н, е = 0,4, Y = 1,5.

4. Минимально необходимые для нор­мальной работы радиально-упорных под­шипников осевые силы:

Рис.29. Расчетная схема к примеру 2

Находим осевые силы, нагружающие подшипники.

Примем F_a1 – F_{a1 min} = 1826Н; тогда из условия равновесия вала следует: F_a2 = F_a1 +F_A= 1826 + 1798 = 3624Н, что больше — F_a2min= 1495Н, следовательно, осевые реакции опор найдены правильно.

5. Отношение F_a1 / F_r1 = 1826 / 5499 = 0,33, что меньше е = 0,4. Тогда для опо­ры 1: Х = 1, У = 0.

Отношение F_a2 / F_r2 = 3624 / 4502 = 0,805, что больше е = 0,4. Тогда для опо­ры 2: X = 0,4, У = 1,5.

6. Эквивалентная динамическая ради­альная нагрузка для подшипников при V = 1; К_Б = 1,4 (см. табл. 69) и К_Т = 1 (t_раб < 100°С) в опорах 1 и 2.

7. Для подшипника более нагруженной опоры 2 вычисляем по формуле (31) рас­четный скорректированный ресурс при а₁ = 1 (вероятность безотказной работы 90%, табл. 68), a₂₃ = 0,6 (обычные условия применения, табл. 70) и k = 10/3 (роли­ковый подшипник)

8. Так как расчетный ресурс больше требуемого: L_10ah > L_10ah′ (21622 > 20000), то предварительно назначенный подшип­ник 7209А пригоден. При требуемом ресур­се надежность несколько выше 90%.

Пример 3. Подобрать подшипники для опор вала червяка (рис. 30). Частота вращения вала 920об/мин. Требуемый ресурс при вероятности безотказной работы 90%:

L_10ah′ = 2000ч. Диаметр посадочных по­верхностей вала d = 30мм. Максимальные, длительно действующие силы: F_{r1 max} = 1000Н, F_{r2 max} = 1200Н, F_Amax = 2200Н.

Рис. 30. Расчетная схема к примеру 3

Режим нагружения — 0 (постоянный). Воз­можны кратковременные перегрузки до 150% номинальной нагрузки. Условия при­менения подшипников — обычные. Ожи­даемая температура работы t_раб = 65°С.

Решение. 1. Для типового режима на­гружения 0 коэффициент эквивалентности K_E= 1,0.

Вычисляем эквивалентные нагрузки:

2. Предварительно назначаем шарико­вые радиально-упорные подшипники лег­кой серии — 36206, угол контакта α = 12°. Схема установки подшипников: 2а (см. рис. 24) – обе опоры фиксирующие; каждая фиксирует вал в одном направлении.

3. Для принятых подшипников из ката­лога находим: Сr = 22000Н, Сor = 12000Н, d= 30мм, D = 62мм, Dw = 9,53мм.

4. Минимально необходимые для нор­мальной работы радиально-упорных под­шипников осевые силы в соответствии с формулами (24), (25):

для опоры 1

Находим осевые силы, нагружающие подшипники.

Примем F_a1 = F_{a1 min} = 347Н, тогда условия равновесия вала следует: F_a2 = F_a1 + F_A = 347 + 2200 = 2547Н, что больше F_a2min= 431Н, следовательно, осевые реакции опор найдены правильно.

5. Дальнейший расчет выполняем более нагруженной опоры 2. По табл. для отношения Dwcosα / Dpw = 9,53 × cos12°/46 = 0,2 находим значение f₀ = 14 , здесь Dpw= 0,5(d + D) = 0,5(30 + 62) = 46. Далее по табл. 64 определяем значение коэффициента е для отношений f₀iF_a2 / Сor = 14 · 1 · 2547 / 12000 = 2,97 : е = 0,49 (определено линейным интерполировав для промежуточных значений «относительной осевой нагрузки» и угла контакта). Отношение F_a2 / F_r2 = 2547 / 1200 = 2,12, что больше е = 0,49. Тогда для опоры (табл. 64): Х= 0,45; Y= 1,11 (определеным линейным интерполированием для значений «относительной осевой нагрузки» 2,! и угла контакта 12°).

6. Эквивалентная динамическая радиальная нагрузка по формуле (27) при V = 1, К_Б =1,3 (см. табл. 69) и К_Т = 1 (t_раб < 100°С)

7. Расчетный скорректированный ресурс, при а₁ = 1 (вероятность безотказной работы 90%, табл. 68), а₂₃ = 0,7 (обычные условия применения, табл. 70) и k = 3 (шариковый подшипник)

8. Так как расчетный ресурс больше требуемого: L10ah > L10ah′ (2317 > 2000), то предварительно назначенный подшипник 36206 пригоден. При требуемом ресурсе надежность несколько выше 90%.

Пример 4. Вычислить скорректирован­ный расчетный ресурс роликовых конических подшипников 1027308А фиксирующей опоры вала червяка (рис. 31). Частота вращения вала n = 970об/мин. Вероятность безотказной работы 95%. Максимальные, длительно действующие силы: F_rmax = 3500Н, F_Amax = 5400Н. Режим нагру­жения — I(тяжелый). Возможны кратковременные перегрузки до 150% номиналь­ной нагрузки. Условия применения под­шипников — обычные. Ожидаемая темпера­тура работы t_раб = 85°С.

Решение. 1. Для переменного типового режима нагруженияI коэффициент эквива­лентности K_E = 0,8 (см. п.6).

Вычисляем эквивалентные нагрузки, при­водя переменный режим нагружения к экви­валентному постоянному:

2. Для роликоподшипника конического с большим углом конусности — условное обозначение 1027308A- по каталогу Сr= 69300Н, е = 0,83.

3. Подшипниковый узел фиксирующей опоры червяка образуют два одинаковых роликовых радиально-упорных конических подшипника, которые рассматривают как один двухрядный подшипник, нагружен­ный силами Fr и Fa = F_A. Для комплекта из двух роликоподшипников имеем С_rсум = 1,714Сr= 1,714 · 69300 = 118780Н.

4. Отношение Fa/ Fr = 4320/2800 = 1,543, что больше е = 0,83. Определим значение угла контакта α (табл. 66):

α = arctg(e / 1,5) = arctg(0,83 / 1,5) = 28,96°.

Тогда для двухрядного роликового радиально-упорного подшипника:

Х= 0,67;

Y=0,67ctgα = 0,67ctg28,96º = 1,21.

5. Эквивалентная динамическая радиальная нагрузка по формуле (27) при V = 1; К_Б = 1,4; К_Т = 1

6. Расчетный скорректированный ресурс а₁ = 0,62 (вероятность безотказной работы 95%, табл. 68), а₂₃ = 0,6 (табл. 70) и k = 10/3 (роликовый подшипник)

Рис. 31. Расчетная схема к примеру 4

Расчет допустимой осевой нагрузки для роликовых радиальных подшипников

Роликоподшипники с короткими ци­линдрическими роликами, как правило, применяют только для восприятия ради­альных сил. Способность роликовых ради­альных подшипников выдерживать осевые нагрузки зависит от конструкции подшип­ника и качества их исполнения.

Подшипники типов 12000, 42000, 62000 и 92000 помимо радиальной могут также воспринимать бортиками колец и торцами роликов относительно небольшие осевые нагрузки, которые в определенных допус­тимых пределах не вызывают снижения расчетного ресурса, при вычислении кото­рого учитывают лишь радиальные силы. Это обусловлено тем, что радиальные силы воспринимают образующие роликов, кон­тактирующие с дорожками качения колец, тогда как осевые силы действуют на борта колец и торцовые поверхности роликов.

При этом важную роль имеют характер нагрузки, частота вращения и смазывание подшипника.

Допустимую осевую нагрузку [Fa] можно определить по формулам:

— для подшипников серий диаметров 1, 2, 3 и 4

— для подшипников серий диаметров 5 и 6

где k_A и k_B — коэффициенты, значения ко­торых приведены в табл. 72 и 73; Сor — ста­тическая грузоподъемность, Н; n — наи­большая частота вращения, об/мин; D и d -соответственно наружный диаметр и диа­метр отверстия подшипника.

При малых частотах вращения допусти­мы случайные кратковременные нагрузки большей величины, но не выше 40% стати­ческой грузоподъемности подшипника.

72. Значения коэффициента k_A

73. Значения коэффициента k_B

Связями называют тела, ограничивающие свободу перемещения рассматриваемого тела.

Реакции связей — это усилия, с которыми связи действуют на данное тело.

Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными.

Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.

Очень важно правильно расставить реакции связей, иначе написанные уравнения окажутся неверными.

Рассмотрим реакции связей основных типов, встречающихся при решении задач: гладкой поверхности, ребра, гибкой нити, стержня, шарнирных опор и заделок, а также примеры замены связей их реакциями.

Реакции гладкой поверхности и ребра

Ниже приведены примеры замены связей гладкой поверхности и ребра их реакциями.
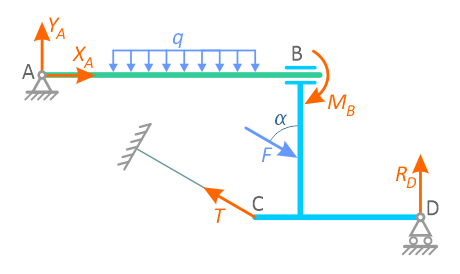
На рисунках 1.1–1.8 показаны примеры замены реакциями сил, расположенных в плоскости.

а – тело весом G на гладкой поверхности;
б – действие поверхности заменено реакцией – силой R;
в – в точке А связь «опорная точка» или ребро;
г – реакции направлены перпендикулярно
опираемой или опирающейся плоскостям

Рисунок 1.1

Реакция гладкой поверхности всегда направлена по нормали к этой поверхности (рисунок 1.1).

Реакции связей нити и стержня

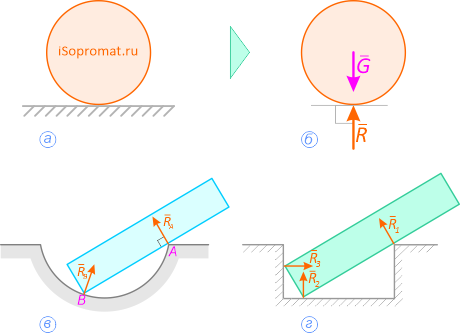
Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль самого троса (нити, цепи, стержня) (рисунок 1.2).

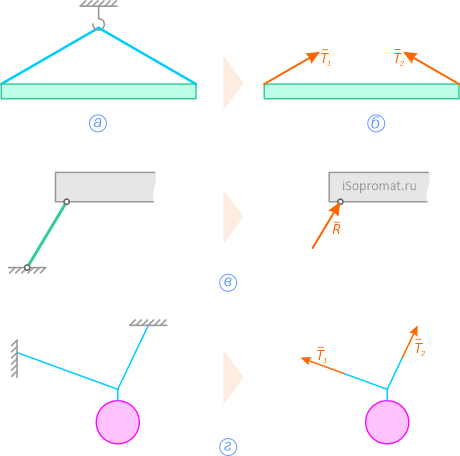
а – балка висит на двух тросах;
б – действие тросов заменено силами Т₁ и Т₂;
в – связь «идеальный стержень»;
г – связь «идеальная нить»

Рисунок 1.2

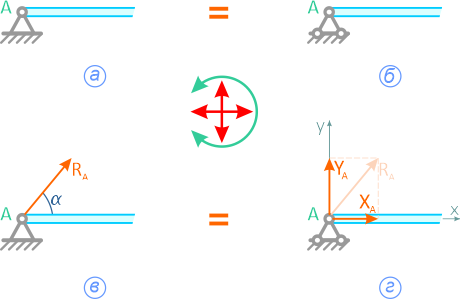
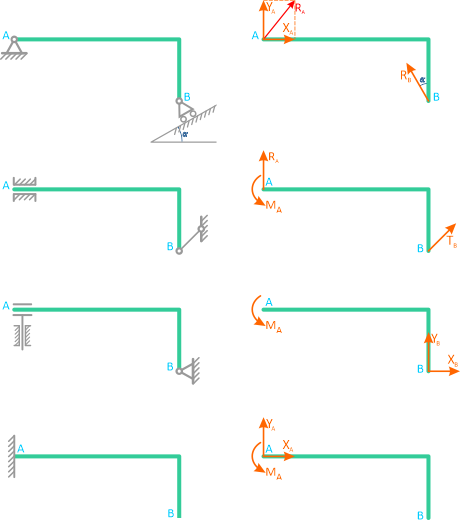
Реакции связей шарнирных опор

Шарнирные опоры допускают вращение относительно шарнира, поэтому в них не возникает вращающий момент.

Шарнирно-неподвижная опора может изображаться по-разному (рисунок 1.3,а или 1.3,б). Она может быть заменена либо силой R с углом α (рисунок 1.3,в), либо двумя силами, например, X_A и Y_A (рисунок 1.3,г).

Рисунок 1.3

Всегда можно перейти от R и α к X_A и Y_A (и наоборот):

Шарнирно-подвижная опора (рисунок 1.4,а, б, в) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное.

Реакция R может быть направлена только по нормали к опорной поверхности (рисунок 1.4, г).

Рисунок 1.4

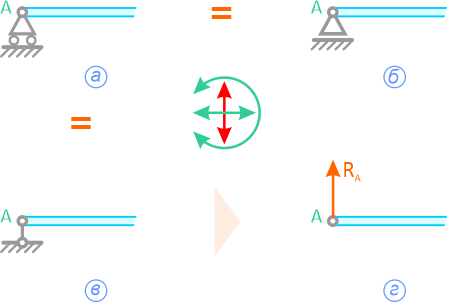
В следующем примере, связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (рисунок 1.5, б), а их действие заменено силами X_A, Y_A и R_B.

Рисунок 1.5

Подробнее про связи и реакции связей смотрите в нашем видео:

Другие видео

Реакции связи в заделках

Все виды заделок исключают поворот, поэтому в них всегда возникает связь «момент».

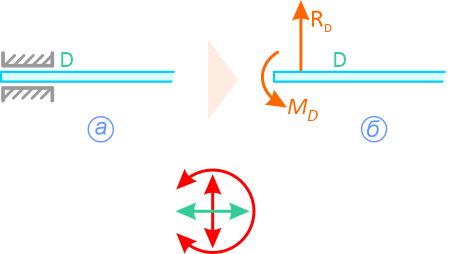
Соединение стержня и втулки в плоскости (рисунок 1.6) – скользящая заделка. Отбросив втулку – получаем действие на стержень силы R_D и момента M_D.

Рисунок 1.6

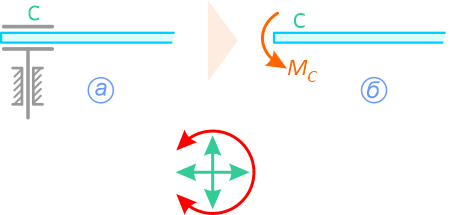
На рисунке 1.7, а изображена бискользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет только момент M_C (рисунок 1.7, б).

Рисунок 1.7

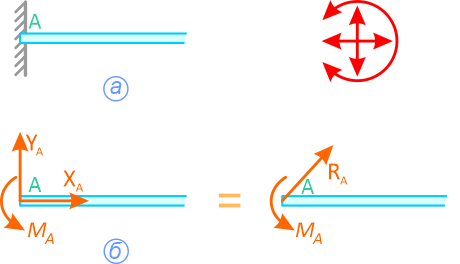
Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила R_A с углом α (или X_A и Y_A) и момент Μ_A (рисунок 1.8).

Рисунок 1.8

Реакции пространственных связей

Трехмерная шарнирно-неподвижная опора, или сферический шарнир (рисунок 1.9, а), заменяется системой сил (рисунок 1.9, б) X_A, Y_A и Z_A, т.е. силой, неизвестной по величине и направлению.

Рисунок 1.9

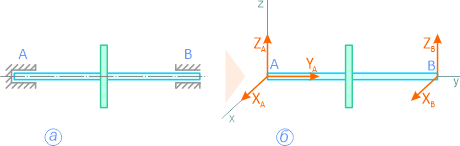
На рисунке 1.10, а показан вал с колесом, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. Действие опор заменено силами X_A, Y_A, Z_A и X_B, Z_B (рисунок 1.10, б).

Рисунок 1.10

На следующих рисунках показаны примеры замены различных типов связей их реакциями.

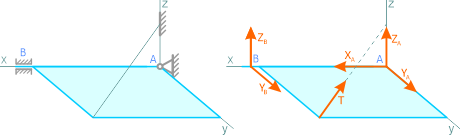
Рисунок 1.11

Трехмерная система удерживаемая в равновесии тремя типами связей: скользящей заделкой, шарнирно неподвижной опорой и тросом.

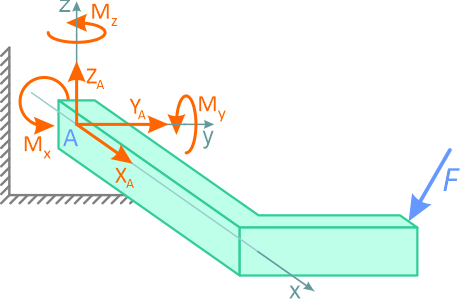
Рисунок 1.12

В общем случае пространственного нагружения, в глухой заделке может возникать до шести реакций связей: три силы и три момента.

Рисунок 1.13

Величина и истинное направление сил реакций связей определяются из уравнений равновесия рассматриваемой системы.
Для плоской системы сил составляется 3 уравнения

Для пространственной системы — до шести уравнений статики.

Из которых выражаются и рассчитываются искомые реакции.

Пример определения сил реакций связей

Задача
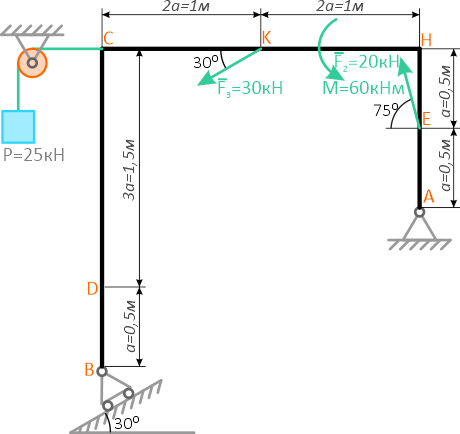
Жесткая рама закреплена в точке A шарнирной связью, а в точке B удерживается в состоянии статического равновесия опорой на катках, с упором в наклонную плоскость под углом 30°.

В точке C к раме привязан трос, перекинутый через блок и несущий на конце груз весом P=25кН.
На раму действует пара сил с моментом M=60кНм и две силы F₂ и F₃ приложенные в точках K и E и расположенные под углами 30° и 75° к горизонтальной оси.

Требуется определить реакции связей в точках A и B, вызываемые заданными действующими нагрузками.
При расчетах, принять размер a=0,5м.

Решение
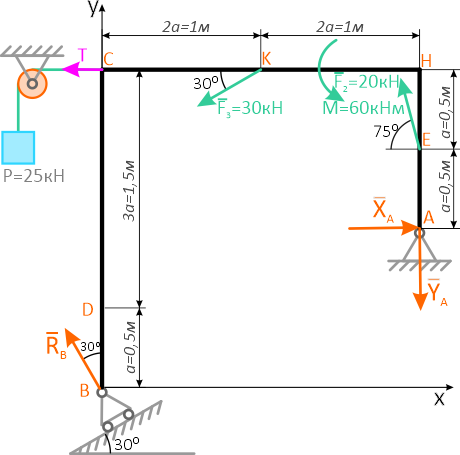
Рассмотрим равновесие рамной пластины.
Проведем координатные оси x-y и изобразим действующие на пластину внешние нагрузки: силы F, пару сил с моментом M, натяжение троса T (по модулю T=P) и реакции связей X_A, Y_A, R_B.

Реакцию неподвижной шарнирной опоры A изображаем двумя составляющими её связями. Реакция на катке направлена перпендикулярно опорной плоскости.
Для полученной плоской системы сил составим три уравнения равновесия системы.

При вычислении моментов сил F относительно точки A воспользуемся теоремой Вариньона, т.е. разложим силы на составляющие F_x=Fcosα и F_y=Fsinα и учтём что m_A(F)=m_A(F_x)+m_A(F_y).

Запишем уравнения сумм проекций сил на оси x и y, а также суммы моментов относительно любой точки системы, например, точки A.

Решая полученную систему уравнений, определяем неизвестные реакции связей катка и шарнирно-неподвижной опоры.

Из уравнения (3) находим реакцию катка

Из уравнения (1) горизонтальную реакцию в точке A

Из уравнения (2) — вертикальную.

Положительные значения найденных реакций говорят о том, что направление связей было выбрано, верно.

Проверку можно выполнить, составив уравнение суммы моментов, в котором будут записаны все искомые реакции, например, относительно точки D:

Ноль, полученный в ответе, означает правильность составления и решения уравнений

Ответ: Получены следующие значения сил реакций связей: в катке R_B=57,6кН, в шарнирной опоре X_A=84,96кН и Y_A=54,2кН.

Другие примеры решения задач >
Проекция силы на ось >