В школьном курсе теорема Вариньона часто фигурирует в качестве обычной задачи, в которой требуется доказать, что середины сторон четырёхугольника являются вершинами параллелограмма.
Её доказательство основано на свойствах средней линии треугольника.
Теорема (Вариньона)
Середины сторон четырёхугольника являются вершинами параллелограмма.
 Дано: ABCD — четырёхугольник,
Дано: ABCD — четырёхугольник,
M, N, K, F — середины его сторон.
Доказать: MNKF — параллелограмм.
Доказательство:
 1) Проведём диагональ AC.
1) Проведём диагональ AC.
2) Рассмотрим треугольник ABC.
Так как точки M и N — середины сторон AB и BC, отрезок MN — средняя линия треугольника ABC.
По свойствам средней линии треугольника,
![]()
![]()
3) Аналогично, FK — средняя линия треугольника ADC и
![]()
![]()
4) По признаку параллельности прямых, две прямые, параллельные третьей прямой, параллельны между собой:
![]()
А так как
![]()
и
![]()
то MN=FK.
5) В четырёхугольнике MKNF противоположные стороны параллельны и равны. Следовательно, MKNF — параллелограмм (по признаку).
Что и требовалось доказать.
Поскольку в школьном курсе геометрии рассматриваются только выпуклые четырёхугольники, доказательство приведено только для этого случая. Но и для невыпуклых четырёхугольников (в том числе, и для самопересекающихся), теорема также верна (доказывается аналогично).
Параллелограмм, образованный серединами сторон четырёхугольника, называется параллелограммом Вариньона (вариньоновским, вариньоновым).
Следствие 1.
Периметр параллелограмма Вариньона равен сумме диагоналей исходного параллелограмма:
![]()
(так как стороны MNKF равны половине диагонали AC или BD).
Следствие 2.
Площадь параллелограмма Вариньона равна половине площади исходного параллелограмма:
![]()
Доказательство:

![]()
![]()
углы COD и NMF равны (как внутренние накрест лежащие при параллельных прямых AC и MN и секущей BD),
![]()
![]()
![]()
Что и требовалось доказать.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 декабря 2021 года; проверки требуют 6 правок.

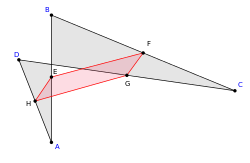
Красный четырёхугольник — параллелограмм
Теоре́ма Вариньо́на — геометрический факт, доказанный Пьером Вариньоном и утверждающий, что середины сторон произвольного четырёхугольника являются вершинами параллелограмма:
Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника.
Параллелограмм, образованный серединами сторон, иногда называется вариньоновским или вариньоновым.
Следствия[править | править код]
- Центр параллелограмма Вариньона лежит на середине отрезка, соединяющего середины сторон исходного четырёхугольника (в этой же точке пересекаются отрезки, соединяющие середины противоположных сторон — диагонали вариньоновского параллелограмма).
- Периметр параллелограмма Вариньона равен сумме диагоналей исходного четырёхугольника.
- Площадь параллелограмма Вариньона равна половине площади исходного четырёхугольника.
- Для прямоугольника и равнобедренной трапеции параллелограммом Вариньона является ромб, а для ромба — прямоугольник.
- Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны 2) бимедианы перпендикулярны.
- Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике: 1) диагонали перпендикулярны; 2) бимедианы равны.
- Параллелограмм Вариньона является квадратом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны и перпендикулярны; 2) бимедианы равны и перпендикулярны.
Доказательство[править | править код]
Доказательство, что площадь параллелограмма равна половине площади исходного четырёхугольника[править | править код]
Пусть диагональ 
















| выпуклый четырёхугольник | невыпуклый четырёхугольник | самопересекающийся четырёхугольник |
|---|---|---|
|
|
|
|
См. также[править | править код]
- Прямая Ньютона
- Теорема Ньютона (планиметрия)
- Четырехугольник
Примечания[править | править код]
Теорема Вариньона
В школьном курсе теорема Вариньона часто фигурирует в качестве обычной задачи, в которой требуется доказать, что середины сторон четырёхугольника являются вершинами параллелограмма.
Её доказательство основано на свойствах средней линии треугольника.
Середины сторон четырёхугольника являются вершинами параллелограмма.
Дано: ABCD — четырёхугольник,
M, N, K, F — середины его сторон.
Доказать : MNKF — параллелограмм.
1) Проведём диагональ AC.
2) Рассмотрим треугольник ABC.
Так как точки M и N — середины сторон AB и BC, отрезок MN — средняя линия треугольника ABC.
3) Аналогично, FK — средняя линия треугольника ADC и
4) По признаку параллельности прямых, две прямые, параллельные третьей прямой, параллельны между собой:
5) В четырёхугольнике MKNF противоположные стороны параллельны и равны. Следовательно, MKNF — параллелограмм (по признаку).
Что и требовалось доказать.
Поскольку в школьном курсе геометрии рассматриваются только выпуклые четырёхугольники, доказательство приведено только для этого случая. Но и для невыпуклых четырёхугольников (в том числе, и для самопересекающихся), теорема также верна (доказывается аналогично).
Параллелограмм, образованный серединами сторон четырёхугольника, называется параллелограммом Вариньона (вариньоновским, вариньоновым).
Периметр параллелограмма Вариньона равен сумме диагоналей исходного параллелограмма:
(так как стороны MNKF равны половине диагонали AC или BD).
Площадь параллелограмма Вариньона равна половине площади исходного параллелограмма:
углы COD и NMF равны (как внутренние накрест лежащие при параллельных прямых AC и MN и секущей BD),
Урок геометрии по теме “Теорема Вариньона. Решение задач”. 8-й класс
Класс: 8
Презентация к уроку
Загрузить презентацию (276 кБ)
Цель: изучить теорему Вариньона и научиться применять ее на практике с наименьшими временными затратами.
Задачи:
- Изучить теоретический материал: понятия «параллелограмм Вариньона», бимедианы четырехугольника, разобрать доказательство теоремы Вариньона и следствия из нее.
- Сравнить количество времени, необходимое для решения задач традиционным способом и, используя теорему Вариньона.
- Показать решение олимпиадных заданий с помощью параллелограмма Вариньона.
Ход урока
Введение
В 21 век, в век информационных технологий, главным ресурсом является время. Тысячи людей желают посещать тренинги, семинары и лекции по тайм-менеджменту, где бы их научили, как рационально, с минимальными потерями и максимальной пользой использовать свое время. Большую часть времени у ученика занимает обучение в школе и приготовление домашнего задания. Одним из самых сложных предметов в школе является геометрия. В частности, задачи на доказательство требуют значительной траты времени, поэтому у многих отсутствует интерес к решению подобных заданий. В теме «Четырехугольники» эту проблему может решить использование теоремы Вариньона.
Пьер Вариньон – французский математик и механик 18 века, который первым доказал, что середины сторон выпуклого четырехугольника являются вершинами параллелограмма. Эта теорема вызвала интерес у отечественных ученых лишь в 20 веке. Подробно ее применение показал украинский геометр – Г.Б.Филипповский и кандидат физико-математических наук, доцент МГУ В.В. Вавилов. В школе теорема Вариньона не входит в курс программы, но считаю изучение её необходимым.
1. Теоретическая часть
Вариньон Пьер [1] (1654–1722)
Пьер Вариньон родился во Франции в 1654 году. Обучался в иезуитском коллеже и университете в Кане, где стал магистром в 1682 году. Вариньон готовился к религиозной деятельности, но, изучая сочинения Эвклида и Декарта, увлекся математикой и механикой. Труды Вариньона посвящены теоретической механике, анализу бесконечно малых, геометрии, гидромеханике и физике. Вариньон был одним из первых ученых, ознакомивших Францию с анализом бесконечно малых. В конце 17 и начале 18 в. Вариньон руководил «Журналом ученых», в котором помещали свои работы по исчислению бесконечно малых братья Бернулли. В геометрии Вариньон изучал различные специальные кривые, в частности ввел термин «логарифмическая спираль». Главные заслуги Вариньона относятся к теоретической механике, а именно к геометрической статике. В 1687 Вариньон представил в Парижскую АН сочинение «Проект новой механики. », в котором сформулировал закон параллелограмма сил. В 1725 в Париже был издан трактат Вариньона «Новая механика или статика», представляющий собой систематическое изложение учения о сложении и разложении сил, о моментах сил и правилах оперирования ими, почти без изменений сохранившееся в учебниках статики до нашего времени. Написал учебник по элементарной геометрии (издан в 1731).
Теорема Вариньона [2]
Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого четырехугольника, является параллелограммом, и его площадь равна половине площади данного четырехугольника.
ABCD – выпуклый четырехугольник
AK=KB; BL=LC; CM=MD; AN=ND
1) KLMN – параллелограмм;
- Рассмотрим одну из сторон четырехугольника KLMN, например KL. KL– средняя линия треугольника ABC(по определению),следовательно, KL║AC. Аналогично, так как MN– средняя линия треугольника ADC,то MN║AC. Так как KL║AC и MN║AC следовательно, KL║NM и KL=MN=AC/2. Таким образом, KLMN – параллелограмм. Этот параллелограмм называется параллелограммом Вариньона данного четырехугольника.
- Средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника,
- т.е. SKBL = SABC/4, SMDN=SADS/4. Следовательно, S1+S3=SABCD /4. Аналогично, S2+S4=SABCD/4. Следовательно, S1+S3 + S2+S4 = SABCD /4 + SABCD/4 = SABCD/2.
Т.е., SKLMN = SABCD/2. Что и требовалось доказать.
Определение. Бимедианы четырехугольниках [3] – это отрезки, соединяющие середины противоположных сторон (диагонали параллелограмма Вариньона)

Следствия из теоремы Вариньона
Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны 2) бимедианы перпендикулярны.

Доказать: KLMN – ромб
Так как AC=BD (диагонали исходного четырехугольника равны по условию), то стороны параллелограмма Вариньона будут равны KL=LM=MN=NK (используя свойство средних линий треугольников, образованных при пересечении диагоналей исходного четырехугольника). Параллелограмм c равными сторонами является ромбом.

KLMN – параллелограмм Вариньона;
KM и LN перпендикулярны
Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом (по признаку ромба).
Что и требовалось доказать.
Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике: 1) диагонали перпендикулярны; 2) бимедианы равны
KLMN – параллелограмм Вариньона;
диагонали AC и BD – перпендикулярны
Так как диагонали AC и BD – перпендикулярны, то стороны параллелограмма Вариньона будут перпендикулярны. Следовательно, параллелограмм Вариньона является прямоугольником.
KLMN – параллелограмм Вариньона;
бимедианы KM и LN – равны
Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником (по признаку прямоугольника).
Что и требовалось доказать.
Параллелограмм Вариньона является квадратом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны и перпендикулярны; 2) бимедианы равны и перпендикулярны
KLMN – параллелограмм Вариньона;
диагонали AC и BD – перпендикулярны; AC=BD
Так как диагонали исходного четырехугольника AC и BD равны и перпендикулярны, то стороны параллелограмма Вариньона будут равны и перпендикулярны. Следовательно, параллелограмм Вариньона является квадратом.
KLMN – параллелограмм Вариньона;
бимедианы KM и LN – перпендикулярны; KM=LN
Доказать: KLMN – квадрат
Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом (по признаку квадрата).
Что и требовалось доказать.
2. Практическая часть. Решение задач.
Докажите, что а) середины сторон прямоугольника являются вершинами ромба. И наоборот, б) середины сторон ромба являются вершинами прямоугольника.
а) Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба (см. следствие 1);
Стороны прямоугольника перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба (см. следствие 1).
б) диагонали ромба перпендикулярны, поэтому середины сторон ромба являются вершинами прямоугольника (см. следствие 2);
Стороны ромба равны, поэтому середины сторон ромба являются вершинами прямоугольника (см. следствие 2).
У четырехугольника диагонали равны aи b. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Периметр параллелограмма Вариньона равен a+b.
Докажите, что середины сторон четырехугольника являются вершинами параллелограмма.
См. теорему Вариньона.
Докажите, что средние линии четырехугольника делятся точкой пересечения пополам.
Т.к. средние линии четырехугольника являются диагоналями параллелограмма Вариньона, то точка пересечения делит их пополам.
Олимпиадные задачи
1. Докажите, что если диагонали четырехугольника равны, то его площадь равна произведению средних линий [5].
Доказать: SABCD= KM*LN
Так как диагонали AC = BD, параллелограмм Вариньона является ромбом, площадь ромба равна половине произведения его диагоналей.
Что и требовалось доказать.
2. Докажите, что суммы площадей накрест лежащих четырехугольников, образованных пересечением бимедиан LN и KM выпуклого четырехугольника ABCD равны [6].
Воспользуемся теоремой о средней линии треугольника.
Что и требовалось доказать.
Заключение
«Нет ничего нового под солнцем, но есть кое-что старое, чего мы не знаем», – сказал американский литератор Лоренс Питер.
Пьер Вариньон жил в 18 веке, но теорема Вариньона как нельзя актуальна именно в наши дни, когда чтобы всё успеть, необходимо гораздо больше, чем 24 часа в сутки.
Поэтому была поставлена цель: изучить теорему Вариньона и научиться применять ее на практике с наименьшими временными затратами.
Для этого был разобран весь теоретический материал, решены задачи базового уровня, а также повышенной сложности (олимпиадные). Было подсчитано, что на решение задачи традиционным способом затрачивается 15-20 минут, а зная теорему Вариньона и следствия из нее, доказательство сводится к одному-двум предложениям и занимает 1-2 минуты. При этом экономия времени на доказательство в среднем составляет 15 минут. Таким образом, уже даже решение трех задач добавит дополнительные сорок пять минут (т.е. целый урок) на доказательство других, более сложных.
От этого повышается не только интерес к изучению данного предмета, но и сам процесс работы приносит удовлетворение. Цель работы считаю достигнутой.
Теорема Вариньона.
Теорема. Середины сторон произвольного четырехугольника являются вершинами параллелограмма, стороны которого равны половинам диагоналей данного четырехугольника, а площадь — половине площади данного четырехугольника.
Пример.
Доказательство.
HE — средняя линия треугольника ABD. Следовательно, HE||BD и HE=0,5·BD.
FG — средняя линия треугольника BCD. Следовательно, FG||BD и FG=0,5·BD.
Следовательно, отрезки HE и FG равны и параллельны, следовательно HEFG — параллелограмм.
Докажем, что площадь параллелограмма HEFG равна половине площади четырехугольника.
Пусть BD∩AC=O, тогда
Пусть EH∩AC=K, тогда ∠BOC=∠EKC как соответственные углы при параллельных прямых HE и BD и секущей AC.
∠EKC=∠EHG как соответственные углы при параллельных прямых AC и HG и секущей EH.
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/644122
http://anasta8ia.ru/teorema-varinona/
[/spoiler]

Теорема. Середины сторон произвольного четырехугольника являются вершинами параллелограмма, стороны которого равны половинам диагоналей данного четырехугольника, а площадь — половине площади данного четырехугольника.
Пример.

Доказательство.
HE — средняя линия треугольника ABD. Следовательно, HE||BD и HE=0,5·BD.
FG — средняя линия треугольника BCD. Следовательно, FG||BD и FG=0,5·BD.
Следовательно, отрезки HE и FG равны и параллельны, следовательно HEFG — параллелограмм.
Докажем, что площадь параллелограмма HEFG равна половине площади четырехугольника.
Пусть BD∩AC=O, тогда
SABCD=0,5·AC·BD·sin∠BOC
SHEFG=HG·HE·sin∠EHG
Пусть EH∩AC=K, тогда ∠BOC=∠EKC как соответственные углы при параллельных прямых HE и BD и секущей AC.
∠EKC=∠EHG как соответственные углы при параллельных прямых AC и HG и секущей EH.
Следовательно, ∠BOC=∠EHG.
SHEFG=HE·HG·sin∠EHG;
SHEFG=HE·HG·sin∠BOC;
SHEFG=0,5·AC·0,5·BD·sin∠BOC;
SHEFG=0,5·0,5·AC·BD·sin∠BOC;
SHEFG=0,5·SABCD.
Цель: изучить теорему Вариньона и научиться применять ее на практике с наименьшими временными затратами.
Задачи:
- Изучить теоретический материал: понятия «параллелограмм Вариньона», бимедианы четырехугольника, разобрать доказательство теоремы Вариньона и следствия из нее.
- Сравнить количество времени, необходимое для решения задач традиционным способом и, используя теорему Вариньона.
- Показать решение олимпиадных заданий с помощью параллелограмма Вариньона.
Ход урока
Введение
В 21 век, в век информационных технологий, главным ресурсом является время. Тысячи людей желают посещать тренинги, семинары и лекции по тайм-менеджменту, где бы их научили, как рационально, с минимальными потерями и максимальной пользой использовать свое время. Большую часть времени у ученика занимает обучение в школе и приготовление домашнего задания. Одним из самых сложных предметов в школе является геометрия. В частности, задачи на доказательство требуют значительной траты времени, поэтому у многих отсутствует интерес к решению подобных заданий. В теме «Четырехугольники» эту проблему может решить использование теоремы Вариньона.
Пьер Вариньон – французский математик и механик 18 века, который первым доказал, что середины сторон выпуклого четырехугольника являются вершинами параллелограмма. Эта теорема вызвала интерес у отечественных ученых лишь в 20 веке. Подробно ее применение показал украинский геометр – Г.Б.Филипповский и кандидат физико-математических наук, доцент МГУ В.В. Вавилов. В школе теорема Вариньона не входит в курс программы, но считаю изучение её необходимым.
1. Теоретическая часть
Вариньон Пьер [1] (1654–1722)
Пьер Вариньон родился во Франции в 1654 году. Обучался в иезуитском коллеже и университете в Кане, где стал магистром в 1682 году. Вариньон готовился к религиозной деятельности, но, изучая сочинения Эвклида и Декарта, увлекся математикой и механикой. Труды Вариньона посвящены теоретической механике, анализу бесконечно малых, геометрии, гидромеханике и физике. Вариньон был одним из первых ученых, ознакомивших Францию с анализом бесконечно малых. В конце 17 и начале 18 в. Вариньон руководил «Журналом ученых», в котором помещали свои работы по исчислению бесконечно малых братья Бернулли. В геометрии Вариньон изучал различные специальные кривые, в частности ввел термин «логарифмическая спираль». Главные заслуги Вариньона относятся к теоретической механике, а именно к геометрической статике. В 1687 Вариньон представил в Парижскую АН сочинение «Проект новой механики…», в котором сформулировал закон параллелограмма сил. В 1725 в Париже был издан трактат Вариньона «Новая механика или статика», представляющий собой систематическое изложение учения о сложении и разложении сил, о моментах сил и правилах оперирования ими, почти без изменений сохранившееся в учебниках статики до нашего времени. Написал учебник по элементарной геометрии (издан в 1731).
Теорема Вариньона [2]
Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого четырехугольника, является параллелограммом, и его площадь равна половине площади данного четырехугольника.
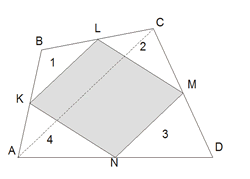 |
Дано: ABCD – выпуклый четырехугольник AK=KB; BL=LC; CM=MD; AN=ND Доказать: 1) KLMN – параллелограмм; 2) SKLMN= SABCD/2 |
Доказательство:
- Рассмотрим одну из сторон четырехугольника KLMN, например KL. KL – средняя линия треугольника ABC (по определению),следовательно, KL║AC. Аналогично, так как MN – средняя линия треугольника ADC,то MN║AC. Так как KL║AC и MN║AC следовательно, KL║NM и KL=MN=AC/2. Таким образом, KLMN – параллелограмм. Этот параллелограмм называется параллелограммом Вариньона данного четырехугольника.
- Средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника,
- т.е. SKBL = SABC/4, SMDN=SADS/4. Следовательно, S1+S3=SABCD /4. Аналогично, S2+S4=SABCD/4. Следовательно, S1+S3 + S2+S4 = SABCD /4 + SABCD/4 = SABCD/2.
Т.е., SKLMN = SABCD/2. Что и требовалось доказать.
Определение. Бимедианы четырехугольниках [3] – это отрезки, соединяющие середины противоположных сторон (диагонали параллелограмма Вариньона)
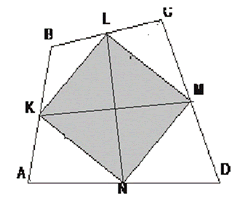
Следствия из теоремы Вариньона
Следствие 1
Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны 2) бимедианы перпендикулярны.
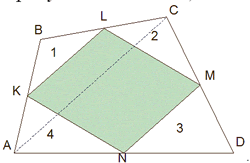 |
Дано: ABCD – четырехугольник; KLMN – параллелограмм Вариньона; AC=BD Доказать: KLMN – ромб |
Доказательство:
Так как AC=BD (диагонали исходного четырехугольника равны по условию), то стороны параллелограмма Вариньона будут равны KL=LM=MN=NK (используя свойство средних линий треугольников, образованных при пересечении диагоналей исходного четырехугольника). Параллелограмм c равными сторонами является ромбом.
2)
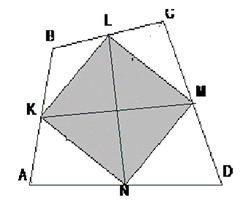 |
Дано: ABCD – четырехугольник; KLMN – параллелограмм Вариньона; KM и LN перпендикулярны Доказать: KLMN – ромб |
Доказательство:
Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом (по признаку ромба).
Что и требовалось доказать.
Следствие 2
Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике: 1) диагонали перпендикулярны; 2) бимедианы равны
1)
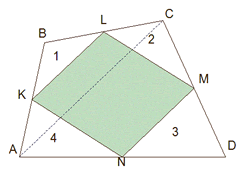 |
Дано: четырехугольник ABCD; KLMN – параллелограмм Вариньона; диагонали AC и BD – перпендикулярны Доказать: KLMN – прямоугольник |
Доказательство:
Так как диагонали AC и BD – перпендикулярны, то стороны параллелограмма Вариньона будут перпендикулярны. Следовательно, параллелограмм Вариньона является прямоугольником.
2)
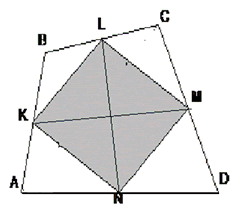 |
Дано: четырехугольник ABCD; KLMN – параллелограмм Вариньона; бимедианы KM и LN – равны Доказать: KLMN – прямоугольник |
Доказательство:
Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником (по признаку прямоугольника).
Что и требовалось доказать.
Следствие 3
Параллелограмм Вариньона является квадратом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны и перпендикулярны; 2) бимедианы равны и перпендикулярны
1)
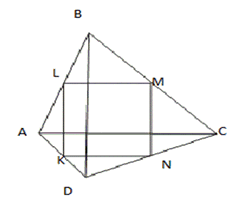 |
Дано: четырехугольник ABCD; KLMN – параллелограмм Вариньона; диагонали AC и BD – перпендикулярны; AC=BD Доказать: KLMN – квадрат |
Доказательство:
Так как диагонали исходного четырехугольника AC и BD равны и перпендикулярны, то стороны параллелограмма Вариньона будут равны и перпендикулярны. Следовательно, параллелограмм Вариньона является квадратом.
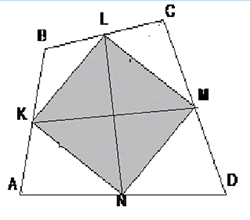 |
Дано: четырехугольник ABCD; KLMN – параллелограмм Вариньона; бимедианы KM и LN – перпендикулярны; KM=LN Доказать: KLMN – квадрат |
Доказательство:
Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом (по признаку квадрата).
Что и требовалось доказать.
2. Практическая часть. Решение задач.
Задача 1 [4]
Докажите, что а) середины сторон прямоугольника являются вершинами ромба. И наоборот, б) середины сторон ромба являются вершинами прямоугольника.
Доказательство:
а) Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба (см. следствие 1);
Стороны прямоугольника перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба (см. следствие 1).
б) диагонали ромба перпендикулярны, поэтому середины сторон ромба являются вершинами прямоугольника (см. следствие 2);
Стороны ромба равны, поэтому середины сторон ромба являются вершинами прямоугольника (см. следствие 2).
Задача 2
У четырехугольника диагонали равны aи b. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Решение:
Периметр параллелограмма Вариньона равен a+b.
Задача 3
Докажите, что середины сторон четырехугольника являются вершинами параллелограмма.
Решение:
См. теорему Вариньона.
Задача 4
Докажите, что средние линии четырехугольника делятся точкой пересечения пополам.
Доказательство:
Т.к. средние линии четырехугольника являются диагоналями параллелограмма Вариньона, то точка пересечения делит их пополам.
Олимпиадные задачи
1. Докажите, что если диагонали четырехугольника равны, то его площадь равна произведению средних линий [5].
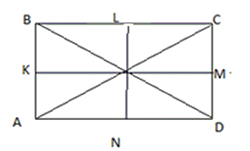 |
Дано: ABCD – четырехугольник; AC = BD Доказать: SABCD= KM*LN |
Доказательство:
Так как диагонали AC = BD, параллелограмм Вариньона является ромбом, площадь ромба равна половине произведения его диагоналей.
Что и требовалось доказать.
2. Докажите, что суммы площадей накрест лежащих четырехугольников, образованных пересечением бимедиан LN и KM выпуклого четырехугольника ABCD равны [6].
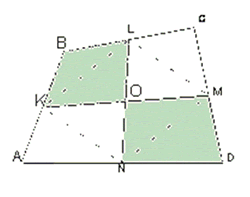
Доказательство:
Воспользуемся теоремой о средней линии треугольника.
Получаем: SBKL + SDMN = (SABC + SADC)/4 = SABCD/4 = (SABD + SCBD)/4 = SAKN+SCLM
Что и требовалось доказать.
Заключение
«Нет ничего нового под солнцем, но есть кое-что старое, чего мы не знаем», – сказал американский литератор Лоренс Питер.
Пьер Вариньон жил в 18 веке, но теорема Вариньона как нельзя актуальна именно в наши дни, когда чтобы всё успеть, необходимо гораздо больше, чем 24 часа в сутки.
Поэтому была поставлена цель: изучить теорему Вариньона и научиться применять ее на практике с наименьшими временными затратами.
Для этого был разобран весь теоретический материал, решены задачи базового уровня, а также повышенной сложности (олимпиадные). Было подсчитано, что на решение задачи традиционным способом затрачивается 15-20 минут, а зная теорему Вариньона и следствия из нее, доказательство сводится к одному-двум предложениям и занимает 1-2 минуты. При этом экономия времени на доказательство в среднем составляет 15 минут. Таким образом, уже даже решение трех задач добавит дополнительные сорок пять минут (т.е. целый урок) на доказательство других, более сложных.
От этого повышается не только интерес к изучению данного предмета, но и сам процесс работы приносит удовлетворение. Цель работы считаю достигнутой.
Список литературы:
- Интернет-ресурсы ru.wikipedia.org/wiki/Вариньон,_Пьер
- Филипповский Г. Б. Параллелограмм Вариньона решает задачи //Математика в школе № 4 – 2006, стр. 45–50
- В. Вавилов, П. Красников. Бимедианы четырехугольника//Математика. 2006 – №22.
- Геометрия: Учебник для 7 – 9 кл. общеобразовательных учреждений /Л. С. Атанасян, В.Ф. Бутузов, С. Б. Кадомцев и др, – М.: Просвещение, 2008.
- Геометрия: Доп. главы к шк. учеб. 8 кл.: Учеб. пособие для учащихся школ и классов с углубленным изучением математики / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 1996.
- Интернет-ресурсы easymath.com.ua/