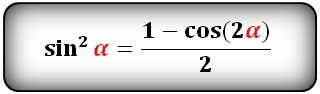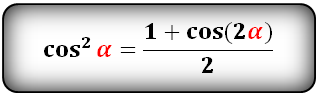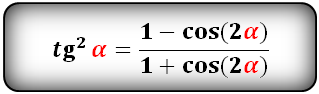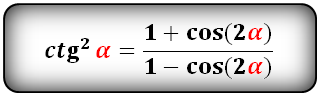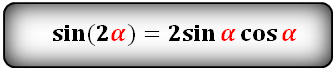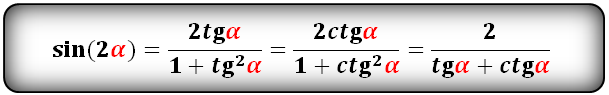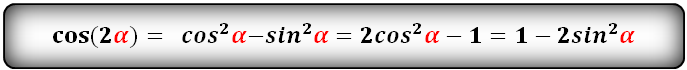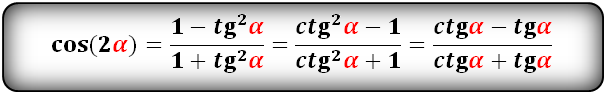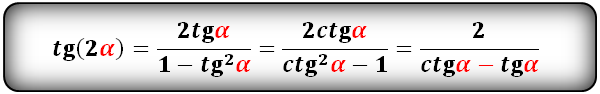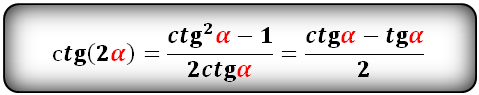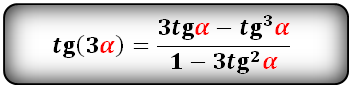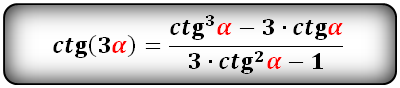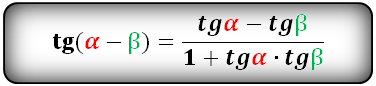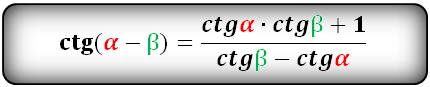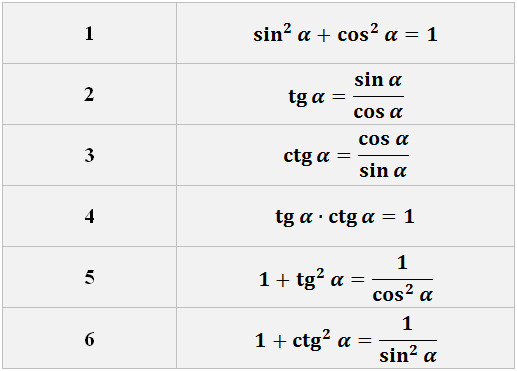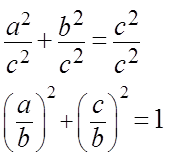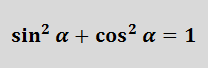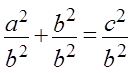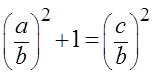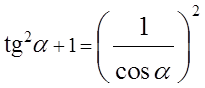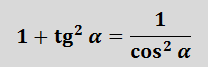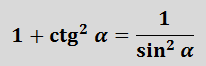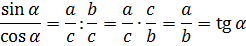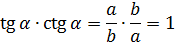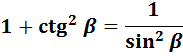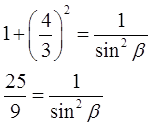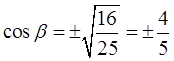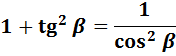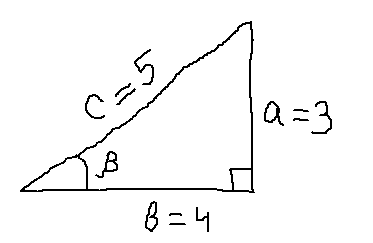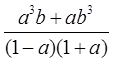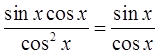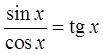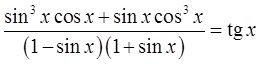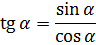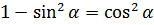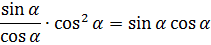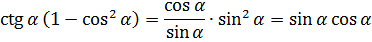Синус в квадрате
Синус (sin) — это тригонометрическая функция, геометрически представляющая отношение противолежащего катета к гипотенузе в прямоугольном треугольнике.
sin 2 (x)=sin(x)*sin(x)
Значение синуса находится в диапазоне от -1 до +1.
Смотрите также калькулятор вычисления синуса угла.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор вычисления квадрата синуса (синуса в квадрате). С помощью этого калькулятора вы в один клик сможете вычислить квадрат синуса любого угла.
Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).
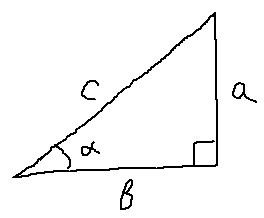
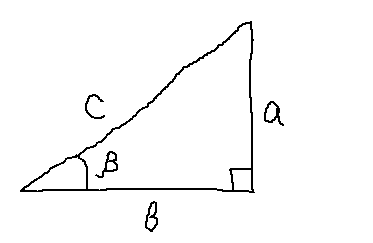
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 — cos 2 α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 — sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
user->isGuest) »]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => »]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else user->identity->profile->first_name) || !empty(Yii::$app->user->identity->profile->surname))user->identity->profile->first_name . ‘ ‘ . Yii::$app->user->identity->profile->surname; > else echo ‘Получайте деньги за каждый набранный балл!’; > ?>—>
Формулы двойного угла в тригонометрии
Формулы двойного угла служат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2 α , используя тригонометрические функции угла α . Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.
Список формул двойного угла
Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид n α записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin n α имеет то же значение, что и sin ( n α ) . При обозначении sin n α имеем аналогичную запись ( sin α ) n . Использование записи применимо для всех тригонометрических функций со степенями n .
Ниже приведены формулы двойного угла:
sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 · sin 2 α , cos 2 α = 2 · cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α c t g 2 α — c t g 2 α — 1 2 · c t g α
Отметим, что данные формулы sin и cos применимы с любым значением угла α . Формула тангенса двойного угла справедлива при любом значении α , где t g 2 α имеет смысл, то есть α ≠ π 4 + π 2 · z , z является любым целым числом. Котангенс двойного угла существует при любом α , где c t g 2 α определен на α ≠ π 2 · z .
Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.
Доказательство формул двойного угла
Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:
sin ( α + β ) = sin α · cos β + cos α · sin β и косинуса суммы cos ( α + β ) = cos α · cos β — sin α · sin β . Предположим, что β = α , тогда получим, что
sin ( α + α ) = sin α · cos α + cos α · sin α = 2 · sin α · cos α и cos ( α + α ) = cos α · cos α — sin α · sin α = cos 2 α — sin 2 α
Таким образом доказываются формулы синуса и косинуса двойного угла sin 2 α = 2 · sin α · cos α и cos 2 α = cos 2 α — sin 2 α .
Остальные формулы cos 2 α = 1 — 2 · sin 2 α и cos 2 α = 2 · cos 2 α — 1 приводят к виду cos 2 α = cos 2 α = cos 2 α — sin 2 α , при замене 1 на сумму квадратов по основному тождеству sin 2 α + cos 2 α = 1 . Получаем, что sin 2 α + cos 2 α = 1 . Так 1 — 2 · sin 2 α = sin 2 α + cos 2 α — 2 · sin 2 α = cos 2 α — sin 2 α и 2 · cos 2 α — 1 = 2 · cos 2 α — ( sin 2 α + cos 2 α ) = cos 2 α — sin 2 α .
Для доказательства формул двойного угла тангенса и котангенса применим равенства t g 2 α = sin 2 α cos 2 α и c t g 2 α = cos 2 α sin 2 α . После преобразования получим, что t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α и c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos α . Разделим выражение на cos 2 α , где cos 2 α ≠ 0 с любым значением α , когда t g α определен. Другое выражение поделим на sin 2 α , где sin 2 α ≠ 0 с любыми значениями α , когда c t g 2 α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:
t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α = 2 · sin α · cos α cos 2 α cos 2 α — sin 2 α cos 2 α = 2 · sin 2 α cos 2 α 1 — sin 2 α cos 2 α = 2 · t g α 1 — t g 2 α c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos = cos 2 α — sin 2 α sin 2 α 2 · sin α · cos α sin 2 α = cos 2 α sin 2 α — 1 2 · cos α sin α = c t g 2 α — 1 2 · c t g α
Примеры использования формул двойного угла
Данный пункт показывает несколько примеров решения с формулами двойного угла. Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2 α для α = 30 ° , применим значения тригонометрических функций для этих углов. Если α = 30 ° , тогда 2 α = 60 ° . Проверим значения sin 60 ° = 2 · sin 30 ° · cos 30 ° , cos 60 ° = cos 2 30 ° — sin 2 30 ° .
Подставив значения, получим t g 60 ° = 2 · t g 30 ° 1 — t g 2 30 ° и c t g 60 ° = c t g 2 30 ° — 1 2 · c t g 30 ° . .
Известно, что sin 30 ° = 1 2 , cos 30 ° = 3 2 , t g 30 ° = 3 3 , c t g 30 ° = 3 и
sin 60 ° = 3 2 , cos 60 ° = 1 2 , t g 60 ° = 3 , c t g 60 ° = 3 3 , тогда отсюда видим, что
2 · sin 30 ° · cos 30 ° = 2 · 1 2 · 3 2 = 3 2 , cos 2 30 ° — sin 2 30 ° = ( 3 2 ) 2 — ( 1 2 ) 2 = 1 2 , 2 · t g 30 ° 1 — t g 2 30 ° = 2 · 3 2 1 — ( 3 3 ) = 3
и c t g 2 30 ° — 1 2 · c t g 30 ° = ( 3 ) 2 — 1 2 · 3 = 3 3
Проведя вычисления, можно сделать вывод, что справедливость для α = 30 ° подтверждена.
Основное использование тригонометрических формул двойного угла – это преобразования тригонометрических выражений. Рассмотрим пример применения двойного угла, года имеем угол, отличный от 2 α . В примере допускается применение формулы двойного угла 3 π 5 . Тогда его необходимо преобразовать, в результате чего получим α = 3 π 5 : 2 = 3 π 10 . Отсюда следует, что формула двойного угла для косинуса будет иметь вид cos 3 π 5 = cos 2 3 π 10 — sin 2 3 π 10 .
Представить sin 2 α 3 через тригонометрические функции, при α 6 .
Заметим, что из условия имеем 2 α 3 = 4 · α 6 . Тогда использовав 2 раза формулу двойного угла, выразим sin 2 α 3 через тригонометрические функции угла α 6 . Применяя формулу двойного угла, получим sin 2 α 3 = 2 · sin α 3 · cos α 3 . После чего к функциям sin α 3 и cos α 3 применим формулы двойного угла: sin 2 α 2 = 2 · sin α 3 · cos α 3 = 2 · ( 2 · sin α 5 · cos α 6 ) · ( cos 2 α 6 — sin α 6 ) = = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6
Ответ: sin 2 α 3 = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6 .
Формулы тройного, четверного и т.д. угла
Таким же образом выводятся формулы тройного, четверного и т.д. углов. Формулы тройного угла можно вывести из формул сложения двойного угла.
sin 3 α = sin ( 2 α + α ) = sin 2 α · cos α + cos 2 α · sin α = 2 · sin α · cos α · cos α + ( cos 2 α — sin 2 α ) · sin α = = 3 · sin α · cos 2 α — sin 3 α
При замене cos 2 α на 1 — sin 2 α из формулы sin 3 α = 3 · sin α · cos 2 α — sin 3 α , она будет иметь вид sin 3 α = 3 · sin α — 4 · sin 3 α .
Так же приводится формула косинуса тройного угла:
cos 3 α = cos ( 2 α + α ) = cos 2 α · cos α — sin 2 α · sin α = = ( cos 2 α — sin 2 α ) · cos α — 2 · sin α · cos α · sin α = cos 3 α — 3 · sin 2 α · cos α
При замене sin 2 α на 1 — cos 2 α получим формулу вида cos 3 α = — 3 · cos α + 4 · cos 3 α .
При помощи полученных формул преобразуем формулу тройного угла для тангенса и котангенса тройного угла:
t g 3 α = sin 3 α cos 3 α = 3 · sin α · cos 2 α — sin 3 α cos 3 α — 3 · sin 2 α · cos α = 3 · sin α · cos 2 α — sin 3 α cos 3 α cos 3 α — 3 · sin 2 α · cos α cos 3 α = = 3 · sin α cos α — sin 3 α cos 3 α 1 — 3 · sin 2 α cos 2 α = 3 · t g α — t g 3 α 1 — 3 · t g 2 α ; c t g 3 α = cos 3 α sin 3 α = cos 3 α — 3 · sin 2 α · cos α 3 · sin α · cos 2 α — sin 3 α = cos 3 α — 3 · sin 2 α · cos α sin 3 α 3 · sin α · cos 2 α — sin 3 α sin 3 α = = cos 3 α sin 3 α — 3 · cos α sin α 3 · cos 2 α sin 2 α — 1 = c t g 3 α — 3 · c t g α 3 · c t g 2 α — 1
Чтобы выводить формулы четвертой степени, имеет смысл представить 4 α как 2 · 2 α , тогда имеет место использование формулы двойного угла два раза. Для выводы формулы 5 степени, представляем 5 α в виде 3 α + 2 α , что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.
Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)
sin(2α)- через sin и cos:
sin(2α)- через tg и ctg:
cos(2α)- через sin и cos:
cos(2α)- через tg и ctg:
tg(2α) и сtg(2α):
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):
Тригонометрические формулы преобразования разности аргументов
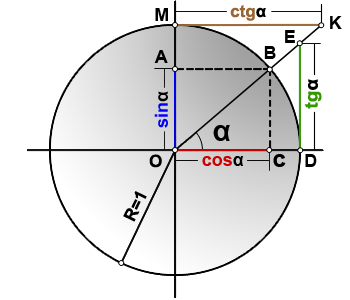
sin(α)=OA
cos(α)=OC
tg(α)=DE
ctg(α)=MK
R=OB=1
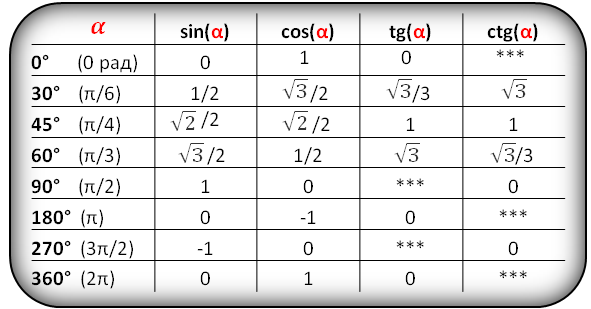
Значения функций для некоторых углов, α
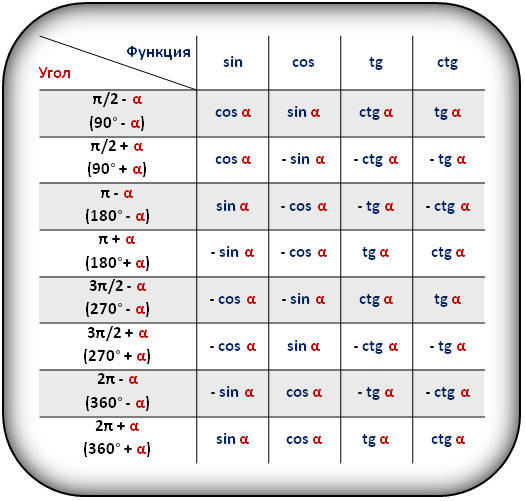
В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).
Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза – сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза – это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс – «x», что не меняет сути).
Синус угла альфа (sin ∠α) – это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) – отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза – это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 – cos 2 α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 – sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
user->isGuest) < echo (Html::a(‘Войдите’, [‘/user/security/login’], [‘class’ =>”]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => ”]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else < if(!empty(Yii::$app->user->identity->profile->first_name) || !empty(Yii::$app->user->identity->profile->surname))< $name = Yii::$app->user->identity->profile->first_name . ‘ ‘ . Yii::$app->user->identity->profile->surname; > else < $name = ”; >echo ‘Получайте деньги за каждый набранный балл!’; > ?>–>
При правильном ответе Вы получите 8 баллов
Упростить выражение с квадратом косинуса:
Выберите всего один правильный ответ.
Добавление комментариев доступно только зарегистрированным пользователям
Lorem iorLorem ipsum dolor sit amet, sed do eiusmod tempbore et dolore maLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborgna aliquoLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempbore et dLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborlore m mollit anim id est laborum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Lorem ipsum dolor sit amet, consectetu sed do eiusmod qui officia deserunt mollit anim id est laborum.
28.01.17 / 22:14, Иван ИвановичОтветить -2
Lorem ipsum dolor sit amet, consectetur adipisicing sed do eiusmod tempboLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod temLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborpborrum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии “на пальцах”.
Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
Или в виде формул:
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
| 0° | 30° | 45° | 60° | 90° | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sin | 0 | 1 | √3 | – | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ctg | – | √3 | 1 |
Принцип повтора знаков тригонометрических функцийУгол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны. Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно. Тригонометрический кругУглы в радианахДля математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π . Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций. Таблица СИНУСОВ для углов от 0° до 360° градусовСИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
Малая таблица значений тригонометрических функций (в радианах и градусах)
Полная таблица синусов для углов от 0° до 360° с шагом всего в 1°
Полная таблица синусов для углов от 91° до 180°
Таблица синусов для углов 181° — 270°
Таблица синусов для углов от 271° до 360° Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе. Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать». Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла. Чему равен синус 45? … – А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071 [spoiler title=”источники:”] http://matematika.club/articles/trigonometry/ http://kvn201.com.ua/table-of-sines.htm [/spoiler] |
Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
При правильном ответе Вы получите 8 баллов
Упростить выражение с квадратом косинуса:
Выберите всего один правильный ответ.
Добавление комментариев доступно только зарегистрированным пользователям
Lorem iorLorem ipsum dolor sit amet, sed do eiusmod tempbore et dolore maLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborgna aliquoLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempbore et dLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborlore m mollit anim id est laborum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Lorem ipsum dolor sit amet, consectetu sed do eiusmod qui officia deserunt mollit anim id est laborum.
Lorem ipsum dolor sit amet, consectetur adipisicing sed do eiusmod tempboLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod temLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborpborrum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Источник
Основное тригонометрическое тождество
9 класс, 10 класс, ЕГЭ/ОГЭ
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
Образовался прямоугольный треугольник OA1B.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Тангенс и котангенс через синус и косинус
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.

Задачка 2. Найдите значение cos α,
если:
Подставляем значения sin α:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Источник
Тригонометрические формулы. Их вывод
Наиболее часто встречающиеся тригонометрические формулы:
(blacktriangleright) Основные тождества: [begin <|l|l|>hline sin^2 alpha+cos^2 alpha =1& mathrm, alpha cdot mathrm, alpha =1 \ &(sinalphane 0, cosalphane 0)\[0.5ex] hline &\ mathrm, alpha=dfrac<sin alpha> <cos alpha>&mathrm, alpha =dfrac<cos alpha> <sin alpha>\&\ 1+mathrm^2, alpha =dfrac1 <cos^2 alpha>& 1+mathrm^2, alpha=dfrac1<sin^2 alpha>\&\ (cosalphane 0)& (sinalphane 0) \ hline end]
(blacktriangleright) Формулы сложения углов: [begin <|l|r|>hline &\ sin<(alphapm beta)>=sinalphacdot cosbetapm sinbetacdot cosalpha & cos<(alphapm beta)>=cosalphacdot cosbeta mp sinalphacdot sinbeta\ &\ hline &\ mathrm, (alphapm beta)=dfrac<mathrm, alphapm mathrm, beta><1 mp mathrm, alphacdot mathrm, beta> & mathrm, (alphapmbeta)=-dfrac<1mp mathrm, alphacdot mathrm, beta><mathrm, alphapm mathrm, beta>\&\ cosalphacosbetane 0&sinalphasinbetane 0\ hline end]
(blacktriangleright) Формулы понижения степени: [begin <|lc|cr|>hline &&&\ sin^2alpha=dfrac<1-cos<2alpha>>2 &&& cos^2alpha=dfrac<1+cos<2alpha>>2\&&&\ hline end]
(blacktriangleright) Формулы произведения функций: [begin <|c|>hline \ sinalphasinbeta=dfrac12bigg(cos<(alpha-beta)>-cos<(alpha+beta)>bigg)\\ cosalphacosbeta=dfrac12bigg(cos<(alpha-beta)>+cos<(alpha+beta)>bigg)\\ sinalphacosbeta=dfrac12bigg(sin<(alpha-beta)>+sin<(alpha+beta)>bigg)\\ hline end]
(blacktriangleright) Выражение синуса и косинуса через тангенс половинного угла: [begin <|l|r|>hline &\ sin<2alpha>=dfrac<2mathrm, alpha><1+mathrm^2, alpha> & cos<2alpha>=dfrac<1-mathrm^2, alpha><1+mathrm^2, alpha>\&\ cosalphane 0 & sinalphane 0\ hline end]
(blacktriangleright) Формула вспомогательного аргумента: [begin <|c|>hline text<Частный случай>\ hline \ sinalphapm cosalpha=sqrt2cdot sin<left(alphapm dfrac<pi>4right)>\\ sqrt3sinalphapm cosalpha=2sin<left(alphapm dfrac<pi>6right)>\\ sinalphapm sqrt3cosalpha=2sin<left(xpm dfrac<pi>3right)>\\ hline text<Общий случай>\ hline\ asinalphapm bcosalpha=sqrtcdot sin<(alphapm phi)>, cosphi=dfrac a<sqrt>, sinphi=dfrac b<sqrt>\\ hline end]
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
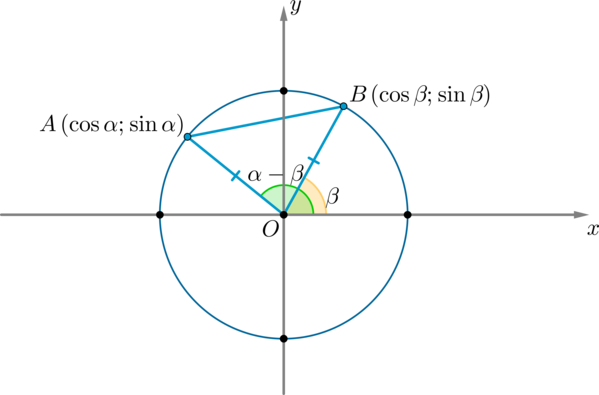
(AB^2=AO^2+BO^2-2AOcdot BOcdot cos(alpha-beta)=1+1-2cos(alpha-beta) (1)) (т.к. (AO=BO=R) – радиус окружности)
По формуле расстояния между двумя точками на плоскости:
Таким образом, сравнивая равенства ((1)) и ((2)) :
Отсюда и получается наша формула.
(blacktriangleright) Вывод остальных формул суммы/разности углов:
Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения (sin x=cos(90^circ-x)) и (cos x=sin (90^circ-x)) :
(blacktriangleright) Вывод формул двойного и тройного углов:
Данные формулы выводятся с помощью предыдущих формул:
1) (sin 2alpha=sin(alpha+alpha)=sinalphacosalpha+sinalphacosalpha=2sinalphacosalpha)
разделим числитель и знаменатель дроби на (cos^2alphane 0) (при (cosalpha=0 Rightarrow mathrm,2alpha=0) ):
5) (sin3alpha=sin(alpha+2alpha)=sinalphacos2alpha+cosalphasin2alpha=sinalpha(1-2sin^2alpha)+cosalphacdot 2sinalphacosalpha=)
6) Аналогично выводится, что (cos3alpha=cos(alpha+2alpha)=4cos^3alpha-3cosalpha)
(blacktriangleright) Вывод формул понижения степени:
Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:
1) (cos2alpha=2cos^2alpha-1 Rightarrow cos^2alpha=dfrac<1+cos2alpha>2)
2) (cos2alpha=1-2sin^2alpha Rightarrow sin^2alpha=dfrac<1-cos2alpha>2)
(blacktriangleright) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
Получим: (cos(alpha+beta)+cos(alpha-beta)=2cosalphacosbeta Rightarrow cosalphacosbeta=dfrac12Big(cos(alpha-beta)+cos(alpha+beta)Big))
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
3) Сложим формулы синуса суммы и синуса разности двух углов:
(blacktriangleright) Вывод формул суммы/разности функций:
Получили формулу суммы косинусов.
Получили формулу разности косинусов.
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
Аналогично выводится формула суммы котангенсов.
(blacktriangleright) Вывод формул выражения синуса и косинуса через тангенс половинного угла:
(разделим числитель и знаменатель дроби на (cos^2alphane 0) (при (cosalpha=0) и (sin2alpha=0) ):)
(blacktriangleright) Вывод формул вспомогательного угла:
Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.
(asin x+bcos x=sqrtleft(dfrac a<sqrt>sin x+ dfrac b<sqrt>cos x right)=sqrtbig(a_1sin x+b_1cos xbig))
(sqrt,big(cos phi sin x+sin phicos xbig)=sqrt,sin (x+phi)) (по формуле синуса суммы двух углов)
Значит, формула выглядит следующим образом: [<large,sin (x+phi),>> quad text <где >cos phi=dfrac a<sqrt>] Заметим, что мы могли бы, например, принять за (cos phi=b_1, sin phi=a_1) и тогда формула выглядела бы как [asin x+bcos x=sqrt,cos (x-phi)]
(blacktriangleright) Рассмотрим некоторые частные случаи формул вспомогательного угла:
(a) sin xpmcos x=sqrt2,left(dfrac1<sqrt2>sin xpmdfrac1<sqrt2>cos xright)=sqrt2, sin left(xpmdfrac<pi>4right))
(b) sqrt3sin xpmcos x=2left(dfrac<sqrt3>2sin xpm dfrac12cos xright)=2, sin left(xpmdfrac<pi>6right))
(c) sin xpmsqrt3cos x=2left(dfrac12sin xpmdfrac<sqrt3>2cos xright)=2,sinleft(xpmdfrac<pi>3right))
Источник
Связь между тригонометрическими функциями одного угла. Основные тригонометрические формулы.
Итак, в прошлый раз мы с вами успешно познакомились с тригонометрическими функциями — синусом, косинусом, тангенсом и котангенсом. И чётко уяснили себе следующее:
1. Синус, косинус, тангенс и котангенс — это просто какие-то безразмерные числа. Отношения сторон в прямоугольном треугольнике. Для каждого конкретного угла — свои.
2. Тригонометрические функции крепко-накрепко связаны с углом. Знаем угол — знаем и все его тригонометрические функции. И наоборот.
Если не уяснили эти простые вещи, то добро пожаловать по ссылочке, пока не поздно. А мы продолжаем.
То, что между этой великолепной четвёркой существует тесная связь, не вызывает никаких сомнений. Всякая связь в математике задаётся, чаще всего, формулами. В тригонометрии формул — огромное количество. Это и формулы приведения, и формулы сложения, двойного угла, понижения степени и многие-многие другие.
Здесь «альфа» — какой-то угол.
Эти шесть формул — краеугольный камень всей тригонометрии. То, чего не знать нельзя. Если вы не знаете, чему равен, скажем, косинус тройного угла — не проблема. Никто вас не осудит. Но если вы не знаете, что sin 2 x+cos 2 x = 1, то будьте готовы получить заслуженную двойку. Вот так вот.
Из этих формул сразу видно, что они неразрывно связывают между собой синус, косинус, тангенс и котангенс одного и того же угла. Именно эти формулы нам позволяют находить все тригонометрические функции одного и того же угла, если известна хотя бы одна из них. Причём (важно!) не находя сам угол! Такие задания очень популярны как сами по себе, так и могут быть промежуточным этапом в более серьёзных заданиях. В тригонометрических уравнениях, к примеру. И особенно в высшей математике, в тех же пределах, интегралах, дифференциальных уравнениях и прочих крутых темах.
Кстати говоря, хочу обратить ваше внимание на один частый ляп в неправильном написании тригонометрических функций в степенях — в квадрате, в кубе и так далее.
Например, выражение квадрат синуса (или синус в квадрате) в тригонометрии пишется вот так:
Двойка (т.е. степень) в этом случае пишется между углом и названием функции. Эта запись как раз и говорит нам о том, что в квадрат возводится именно сама функция (т.е. в нашем случае — синус).
будет говорить уже о том, что в квадрат возводится, не синус угла, а только сам угол! Почувствуйте разницу, что называется.)
Во избежание путаницы, ещё раз (и навсегда!) всё то же самое, но со скобочками:
sin 2 x = (sin x) 2
sin x 2 = sin(x 2 )
Конечно, заниматься возведением углов в квадрат мы в школьной тригонометрии вряд ли будем. За ненадобностью.) Зато возведением функций в квадрат — постоянно. Так что привыкаем, не путаемся и пишем правильно.
Ну что, посмотрим на вывод основных формул? Чтобы всё встало на свои места. Зачем и почему? Да потому, что любая формула запоминается гораздо проще, если есть возможность её «пощупать» в реале, а не механически зазубривать и бездумно принимать на веру, как само собой разумеющееся.) Тем более что это не просто, а очень просто!
Вывод и смысл основных тригонометрических формул.
Первым делом, я снова нарисую наш старый добрый прямоугольный треугольник. Не обязательно по линеечке, по клеточкам, а просто схематично. От руки.
Что нам понадобится ещё для дальнейшей работы?
1. Теорема Пифагора:
a 2 + b 2 = c 2
sin α = a/c
cos α = b/c
tg α = a/b
ctg α = b/a
Всё. Вот и все инструменты.
А вот теперь начинается самое весёлое. Сейчас я беру нашу горячо любимую теорему Пифагора a 2 + b 2 = c 2 и… начинаю всячески над ней издеваться, подвергая её всевозможным пыткам.) Результатами пыток станут целых три формулы из нашего списка!
Так у нас с вами рождается на свет формула №1:
Эта формула — самая популярная во всей тригонометрии! По-другому её ещё называют основным тригонометрическим тождеством.
Она же, но записанная слегка по-другому (в зависимости от того, что именно надо выразить):
Эти две модификации формулы №1 весьма и весьма часто применяются в примерах по тригонометрии! Именно они позволяют легко перевращать синусы в косинусы (и наоборот). Имеет смысл запомнить.
Давайте поделим и посмотрим:
И снова соображаем из тригонометрии (и нашего рисунка), что же такое a/b. Верно, тангенс альфа! А c/b? Так сразу и не скажешь… Стоп! Но ведь что такое b/c — это же нам ясно! Это косинус альфа! У нас же в формуле стоит тот же косинус, только перевёрнутый вверх ногами — c/b. Значит, справа в скобках у нас стоит величина, обратная косинусу: 1/cos α.
Итого имеем следующее:
Переписываем в привычном виде и рождаем формулу №5:
Попробуйте получить самостоятельно, очень полезно.)
Вторая, третья и четвёртая формулы выводятся совсем элементарно, исходя только из определения тригонометрических функций и элементарных действий с дробями. Теорема Пифагора здесь не нужна.
Что, например, у нас получится, если мы просто поделим синус на косинус?
И все дела.) С котангенсом — аналогично.
А если перемножить тангенс и котангенс? Ну-ка, ну-ка…
Вот и вся премудрость. Убедились, насколько всё просто?)
Решение простейших заданий по тригонометрии.
Теория теорией, но нам ведь опыт наращивать надо, верно? Так что пора приступать к задачкам. Всё как всегда — от совсем простых и безобидных до вполне себе серьёзных.
Здесь, ясное дело, надо искать формулу, связывающую тангенс и котангенс. Это четвёртая формула. Самое главное — сообразить, что вместо «альфа» можно писать любую другую букву. Лишь бы везде одна и та же была. Для нашего задания будет:
Можно прямо в эту формулу подставить значение ctg x = 1,25:
Осталось лишь решить это простенькое уравнение. Да-да. Ещё раз подчёркиваю, что любая формула, любое соотношение, соединённое знаком равенства («=»), — это всегда уравнение! А там, где уравнение, там автоматически и тождественные преобразования уравнений, да…
Наше соотношение — это тоже уравнение. Где роль неизвестного играет tg x. Прошу заметить, не икс, а именно весь тангенс целиком! Вас же не смущает уравнение, скажем, y·1,25 = 1? Что вы обычно делаете в таких случаях? Правильно, делите обе части на 1,25, чтобы слева остался чистый игрек. Вот и здесь тоже делим обе части на 1,25, добиваясь слева чистого тангенса.
И все дела. Это и есть верный ответ.
Можно поступить иначе. Сначала выразить из общей формулы тангенс:
А уже теперь подставить вместо ctg x его значение 1,25. Получим то же самое. И так и эдак можно. Разницы — никакой. Но… если осознать смысл этой формулы поглубже, то можно получить очень простой и очень полезный практический приём.
Запоминаем:
Если единицу разделить на котангенс, то получим тангенс. И наоборот, единица, делённая на тангенс, даёт котангенс. Эти две функции взаимно обратны!
Что? Не знаете, как разделить единичку на число? Ну, это вопрос не к тригонометрии. Вопрос к шестому классу, к дробям… Как разделить? Да просто перевернуть это самое число и все дела!
И так далее и тому подобное. В общем, вы поняли…)
Например, классика жанра:
2. Известно, что β — острый угол в прямоугольном треугольнике.
Ищем формулу, связывающую синус и косинус. Это самая первая формула:
Подставляем в неё известную нам величину 0,6 вместо косинуса:
И считаем, как обычно:
Вот, практически, и всё. У нас есть квадрат синуса. А нужен сам синус. Для этого осталось всего лишь извлечь корень и — ответ готов! Корень из 0,64 будет 0,8.
Два разных ответа получается. А нужен один. Второй — неправильный. Что делать? Да всё как обычно! Внимательно прочитать задание! Там зачем-то сказано: «… если β — острый угол…» А лишних слов в заданиях, как правило, не бывает, да… Именно эти слова — и есть дополнительная информация к решению.
Что такое острый угол? Это угол меньше 90 градусов. А у таких углов все тригонометрические функции (в том числе и синус, да…) всегда положительные. То есть, отрицательный ответ мы здесь просто отбрасываем. Имеем полное право.
Собственно, на данном этапе нам такие тонкости особо не нужны. Пока… Ибо сейчас мы работаем только с прямоугольными треугольниками, где углы могут быть только острые. И не знаем, счастливые, что бывают и отрицательные углы, и углы в 1000 градусов… И у всех этих жутких углов тоже есть свои тригонометрические функции! С плюсом и с минусом. Всё от конкретного угла зависит.
А вот старшеклассникам без учёта знака — никак. К сожалению… Но не будем бежать впереди паровоза. Всему своё время.)
Решаем следующую задачку. Покруче.
Определить косинус острого угла β в прямоугольном треугольнике, если ctgβ = 4/3.
На первый взгляд, всё просто. Но попробуем найти в нашем списке формулу, связывающую котангенс и косинус. Ищем и… Вы правы! Такой формулы нету.) Надо как-то выкручиваться…
Можно работать с шестой формулой:
Подставим в эту формулу значение котангенса и преобразуем:
Выразим из этой пропорции (т.е. тоже уравнения!) квадрат синуса:
Итак, квадрат синуса у нас есть. Теперь его легко можно превратить в квадрат косинуса по первой формуле:
cos 2 β = 1 — sin 2 β
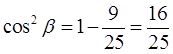
Извлекаем корень и определяем сам косинус:
Читаем ещё раз задание и вспоминаем, что у острого угла все тригонометрические функции всегда положительны. Отбрасываем отрицательное значение и получаем окончательный ответ:
Это был один способ. Можно решать и по-другому, через пятую формулу:
Для этого нам надо:
1) Превратить котангенс в тангенс по формуле №4;
2) Подставить значение тангенса в формулу;
3) Преобразовать выражение и выразить из него квадрат косинуса;
4) Извлечь корень и получить два значения косинуса;
5) Сообразить (из условия задания), что в прямоугольном треугольнике все тригонометрические функции всегда положительны. Отбросить отрицательный ответ и получить косинус.
Как видим, хрен редьки не слаще, да.) Но это ещё не всё. Для такого решения надо ещё вспомнить эти формулы! А если забыли? Собственно, в этом-то и кроется главная проблема в их применении. Да ещё и куча вычислений… В общем, не подарок…
Без паники! Для таких задачек есть очень простой и, главное, наглядный способ решения! Геометрический.) Читаем, вникаем и запоминаем.
Нарисуем этот котангенс!
Да-да! Схематично. Как? Очень просто! Берём черновик и рисуем любой прямоугольный треугольник. Кривовато, от руки, даже не соблюдая пропорций. У нас не ИЗО и не черчение с вами.) Выбираем любой острый угол и обозначаем его «бета».
Вспоминаем теперь, что котангенс — это отношение прилежащего катета к противолежащему. И ставим на соответствующих катетах их длины. Какие? А какие в нашем котангенсе записаны! 4 и 3. Противолежащий катет a = 3, а прилежащий b = 4.
Чего ещё нам не хватает для полного счастья? Гипотенузы нам не хватает! Не беда: Пифагор ещё никого не подводил.)
Итак, гипотенуза равна пяти. Подписываем на картинке.)
А теперь считаем косинус прямо по заклинанию: отношение прилежащего катета к гипотенузе.
Всё! Быстро, правда?) Вот такой красивый графический способ-лайт. Безо всяких формул.) Ну… почти. Ведь теорему Пифагора всяко надо знать, да.)
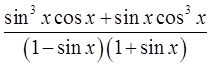
Что, внушает? В таких замороченных примерах необходимо понимать, что синусы и косинусы никоим образом не отменяют всей остальной математики. И подчиняются тем же самым общим правилам, что и обычные числа и буквы в алгебре! А именно — разложение на множители, формулы сокращённого умножения, раскрытие скобок, приведение подобных, сокращение дробей и т.п.
Вас же никак не смущает дробь
правда ведь? Хотя кого-то она, возможно, тоже смущает, да…
Естественно, к основным правилам алгебры добавляется ещё и специфика самой тригонометрии, от этого никуда не денешься. Собственно, с этой целью и разбираем соответствующий пример, да.)
Начнём с числителя нашей здоровенной дроби. Забудем на минутку про тригонометрию и прикинем, что там можно сделать, основываясь на обычных правилах алгебры. Да хотя бы вынести один синус за скобки! Верно, давайте вынесем:
sin 3 x·cos x + sin x·cos 3 x = sin x (sin 2 x·cos x+cos 3 x)
Ой, ещё и косинус вынести можно!
sin x (sin 2 x·cos x+cos 3 x) = sin x·cos x (sin 2 x+cos 2 x)
Вот так. Самые грамотные вообще сразу целиком вынесут произведение sin x·cos x за скобку. Знания и наблюдательность иногда очень помогают. Если они есть.)
А вот теперь и тригонометрия в дело вступает! Что у нас в скобочках? Да! В скобочках у нас — чистая формула №1. Или основное тригонометрическое тождество:
От умножения на единичку выражение не меняется. Значит, числитель нашей дроби будет не что иное, как просто sin x·cos x.
Всё. Числитель упростили до упора. Работаем со знаменателем:
А здесь что? Разность ква… Точно! Разность квадратов! Такая родная и знакомая формула:
Под буквой «a» здесь скрывается единичка, а под буквой «b» — выражение sin x. Ну и что? Важно понимать, что под буквами в алгебраических выражениях может скрываться всё что угодно! И числа, и синусы, и логарифмы, и степени — любые сложные выражения! Алгебре все выражения по плечу. Иначе она не была бы алгеброй, да…)
Вот и срабатываем прямо по формуле разности квадратов:
(1–sin x)(1+sin x) = 1 2 — (sin x) 2 = 1 — sin 2 x
А вот теперь соображаем, уже из тригонометрии, что
Вставляем упрощённые числитель и знаменатель в нашу дробь, сокращаем что сокращается и получаем:
Казалось бы, всё. В рамках алгебры 7-го класса такая дробь дальнейшему упрощению уже не поддаётся, но алгебра в этом примере и так постаралась на славу. Зато в рамках тригонометрии эта дробь вполне себе упрощается! Что же такое синус поделить на косинус? Тангенс, конечно же! Чистая формула №2.
Вот теперь всё. Значит, окончательный результат упрощения вот такой:
Эффект потрясающий, правда?
Запоминаем:
В тригонометрии очень популярны задания, где надо использовать алгебру 7-го класса. А именно — разложение на множители, формулы сокращённого умножения, раскрытие скобок, приведение подобных, сокращение дробей и т.п. Проверяем замороченные примеры на алгебру 7-го класса!
Ещё из той же оперы:
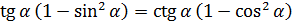
Напоминаю, что страшная фраза «доказать тождество» всего лишь означает, что надо упростить обе части предлагаемого равенства (или какую-то одну, более сложную) и убедиться, что слева и справа стоит одно и то же выражение.
Вот и пробуем добраться до одинакового выражения! Начинаем с левой части. Превращаем тангенс в отношение синуса к косинусу по второй формуле:
Выражение в скобках превращаем в квадрат косинуса по первой формуле:
Подставляем, сокращаем косинусы и получаем:
Ну вот. Левая часть упрощена по максимуму. С правой частью аналогично — формулы №1 и №3 нам в помощь:
Вот и всё! Слева и справа мы получили совершенно одинаковые выражения! А именно — sinα·cosα. Что и требовалось доказать.)
Итак, самое главное.
Чётко уясняем: тригонометрические функции (синус, косинус, тангенс и котангенс) одного угла неразрывно связаны между собой основными тригонометрическими формулами. Если нам известна хотя бы одна из функций — значит, можно (при наличии необходимой дополнительной информации) вычислить и все остальные!
А теперь порешаем, как обычно.
1. Косинус острого угла равен 7/25. Найдите синус этого угла.
2. Известно, что β — угол в прямоугольном треугольнике. Найти tgβ, если sinβ = 15/17.
3. Найдите косинус острого угла A, если известно, что ctg A = 2,4.
5. Упростите выражение и найдите его значение, если sinβ = 1:
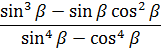
6. Известно, что tg y = 3. Найдите значение выражения:
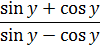
Что, страшно? Мы такого не решали? Да, не решали. Но и самим поразмышлять тоже иногда полезно, да.) Подсказка: основное свойство дроби вам в помощь! Ну и формула №2 для тангенса, само собой.)
Источник
Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
При правильном ответе Вы получите 8 баллов
Упростить выражение с квадратом косинуса:
Выберите всего один правильный ответ.
Добавление комментариев доступно только зарегистрированным пользователям
Lorem iorLorem ipsum dolor sit amet, sed do eiusmod tempbore et dolore maLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborgna aliquoLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempbore et dLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborlore m mollit anim id est laborum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Lorem ipsum dolor sit amet, consectetu sed do eiusmod qui officia deserunt mollit anim id est laborum.
Lorem ipsum dolor sit amet, consectetur adipisicing sed do eiusmod tempboLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod temLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborpborrum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Источник
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение тригонометрических уравнений.
Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Немного теории.
Тригонометрические уравнения
Уравнение cos(х) = а
Уравнение cos x = а, где ( |a| leqslant 1 ), имеет на отрезке ( 0 leqslant x leqslant pi ) только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac<pi> <2>right] ); если a
Уравнение tg(х) = а
Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.
Решение тригонометрических уравнений
Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.
Уравнения, сводящиеся к квадратным
Уравнение вида a sin(x) + b cos(x) = c
Используя формулы ( sin(x) = 2sinfrac <2>cosfrac<2>, ; cos(x) = cos^2 frac <2>-sin^2 frac <2>) и записывая правую часть уравпения в виде ( 2 = 2 cdot 1 = 2 left( sin^2 frac <2>+ cos^2 frac <2>right) ) получаем
В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях ( a neq 0, ; b neq 0, ; c neq 0, ; c^2 leqslant b^2+c^2 ) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на ( sqrt ):
Решить уравнение 4 sin(x) + 3 cos(x) = 5
Здесь a = 4, b = 3, ( sqrt = 5 ). Поделим обе части уравнения на 5:
Уравнения, решаемые разложением левой части на множители
Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.
Источник
Таблица СИНУСОВ для углов от 0° до 360° градусов
СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
| α (радианы) | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π | |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| SIN α (СИНУС) | 1/2 | √ 2/2 | √3 /2 | 1 | -1 |
Малая таблица значений тригонометрических функций (в радианах и градусах)
| Угол в градусах | Sin (Синус) |
|---|---|
| 0° | |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0523 |
| 4° | 0.0698 |
| 5° | 0.0872 |
| 6° | 0.1045 |
| 7° | 0.1219 |
| 8° | 0.1392 |
| 9° | 0.1564 |
| 10° | 0.1736 |
| 11° | 0.1908 |
| 12° | 0.2079 |
| 13° | 0.225 |
| 14° | 0.2419 |
| 15° | 0.2588 |
| 16° | 0.2756 |
| 17° | 0.2924 |
| 18° | 0.309 |
| 19° | 0.3256 |
| 20° | 0.342 |
| 21° | 0.3584 |
| 22° | 0.3746 |
| 23° | 0.3907 |
| 24° | 0.4067 |
| 25° | 0.4226 |
| 26° | 0.4384 |
| 27° | 0.454 |
| 28° | 0.4695 |
| 29° | 0.4848 |
| 30° | 0.5 |
| 31° | 0.515 |
| 32° | 0.5299 |
| 33° | 0.5446 |
| 34° | 0.5592 |
| 35° | 0.5736 |
| 36° | 0.5878 |
| 37° | 0.6018 |
| 38° | 0.6157 |
| 39° | 0.6293 |
| 40° | 0.6428 |
| 41° | 0.6561 |
| 42° | 0.6691 |
| 43° | 0.682 |
| 44° | 0.6947 |
| 45° | 0.7071 |
| 46° | 0.7193 |
| 47° | 0.7314 |
| 48° | 0.7431 |
| 49° | 0.7547 |
| 50° | 0.766 |
| 51° | 0.7771 |
| 52° | 0.788 |
| 53° | 0.7986 |
| 54° | 0.809 |
| 55° | 0.8192 |
| 56° | 0.829 |
| 57° | 0.8387 |
| 58° | 0.848 |
| 59° | 0.8572 |
| 60° | 0.866 |
| 61° | 0.8746 |
| 62° | 0.8829 |
| 63° | 0.891 |
| 64° | 0.8988 |
| 65° | 0.9063 |
| 66° | 0.9135 |
| 67° | 0.9205 |
| 68° | 0.9272 |
| 69° | 0.9336 |
| 70° | 0.9397 |
| 71° | 0.9455 |
| 72° | 0.9511 |
| 73° | 0.9563 |
| 74° | 0.9613 |
| 75° | 0.9659 |
| 76° | 0.9703 |
| 77° | 0.9744 |
| 78° | 0.9781 |
| 79° | 0.9816 |
| 80° | 0.9848 |
| 81° | 0.9877 |
| 82° | 0.9903 |
| 83° | 0.9925 |
| 84° | 0.9945 |
| 85° | 0.9962 |
| 86° | 0.9976 |
| 87° | 0.9986 |
| 88° | 0.9994 |
| 89° | 0.9998 |
| 90° | 1 |
Полная таблица синусов для углов от 0° до 360° с шагом всего в 1°
| Угол в градусах | Sin (Синус) |
|---|---|
| 91° | 0.9998 |
| 92° | 0.9994 |
| 93° | 0.9986 |
| 94° | 0.9976 |
| 95° | 0.9962 |
| 96° | 0.9945 |
| 97° | 0.9925 |
| 98° | 0.9903 |
| 99° | 0.9877 |
| 100° | 0.9848 |
| 101° | 0.9816 |
| 102° | 0.9781 |
| 103° | 0.9744 |
| 104° | 0.9703 |
| 105° | 0.9659 |
| 106° | 0.9613 |
| 107° | 0.9563 |
| 108° | 0.9511 |
| 109° | 0.9455 |
| 110° | 0.9397 |
| 111° | 0.9336 |
| 112° | 0.9272 |
| 113° | 0.9205 |
| 114° | 0.9135 |
| 115° | 0.9063 |
| 116° | 0.8988 |
| 117° | 0.891 |
| 118° | 0.8829 |
| 119° | 0.8746 |
| 120° | 0.866 |
| 121° | 0.8572 |
| 122° | 0.848 |
| 123° | 0.8387 |
| 124° | 0.829 |
| 125° | 0.8192 |
| 126° | 0.809 |
| 127° | 0.7986 |
| 128° | 0.788 |
| 129° | 0.7771 |
| 130° | 0.766 |
| 131° | 0.7547 |
| 132° | 0.7431 |
| 133° | 0.7314 |
| 134° | 0.7193 |
| 135° | 0.7071 |
| 136° | 0.6947 |
| 137° | 0.682 |
| 138° | 0.6691 |
| 139° | 0.6561 |
| 140° | 0.6428 |
| 141° | 0.6293 |
| 142° | 0.6157 |
| 143° | 0.6018 |
| 144° | 0.5878 |
| 145° | 0.5736 |
| 146° | 0.5592 |
| 147° | 0.5446 |
| 148° | 0.5299 |
| 149° | 0.515 |
| 150° | 0.5 |
| 151° | 0.4848 |
| 152° | 0.4695 |
| 153° | 0.454 |
| 154° | 0.4384 |
| 155° | 0.4226 |
| 156° | 0.4067 |
| 157° | 0.3907 |
| 158° | 0.3746 |
| 159° | 0.3584 |
| 160° | 0.342 |
| 161° | 0.3256 |
| 162° | 0.309 |
| 163° | 0.2924 |
| 164° | 0.2756 |
| 165° | 0.2588 |
| 166° | 0.2419 |
| 167° | 0.225 |
| 168° | 0.2079 |
| 169° | 0.1908 |
| 170° | 0.1736 |
| 171° | 0.1564 |
| 172° | 0.1392 |
| 173° | 0.1219 |
| 174° | 0.1045 |
| 175° | 0.0872 |
| 176° | 0.0698 |
| 177° | 0.0523 |
| 178° | 0.0349 |
| 179° | 0.0175 |
| 180° |
Полная таблица синусов для углов от 91° до 180°
| Угол | Sin (Синус) |
|---|---|
| 181° | -0.0175 |
| 182° | -0.0349 |
| 183° | -0.0523 |
| 184° | -0.0698 |
| 185° | -0.0872 |
| 186° | -0.1045 |
| 187° | -0.1219 |
| 188° | -0.1392 |
| 189° | -0.1564 |
| 190° | -0.1736 |
| 191° | -0.1908 |
| 192° | -0.2079 |
| 193° | -0.225 |
| 194° | -0.2419 |
| 195° | -0.2588 |
| 196° | -0.2756 |
| 197° | -0.2924 |
| 198° | -0.309 |
| 199° | -0.3256 |
| 200° | -0.342 |
| 201° | -0.3584 |
| 202° | -0.3746 |
| 203° | -0.3907 |
| 204° | -0.4067 |
| 205° | -0.4226 |
| 206° | -0.4384 |
| 207° | -0.454 |
| 208° | -0.4695 |
| 209° | -0.4848 |
| 210° | -0.5 |
| 211° | -0.515 |
| 212° | -0.5299 |
| 213° | -0.5446 |
| 214° | -0.5592 |
| 215° | -0.5736 |
| 216° | -0.5878 |
| 217° | -0.6018 |
| 218° | -0.6157 |
| 219° | -0.6293 |
| 220° | -0.6428 |
| 221° | -0.6561 |
| 222° | -0.6691 |
| 223° | -0.682 |
| 224° | -0.6947 |
| 225° | -0.7071 |
| 226° | -0.7193 |
| 227° | -0.7314 |
| 228° | -0.7431 |
| 229° | -0.7547 |
| 230° | -0.766 |
| 231° | -0.7771 |
| 232° | -0.788 |
| 233° | -0.7986 |
| 234° | -0.809 |
| 235° | -0.8192 |
| 236° | -0.829 |
| 237° | -0.8387 |
| 238° | -0.848 |
| 239° | -0.8572 |
| 240° | -0.866 |
| 241° | -0.8746 |
| 242° | -0.8829 |
| 243° | -0.891 |
| 244° | -0.8988 |
| 245° | -0.9063 |
| 246° | -0.9135 |
| 247° | -0.9205 |
| 248° | -0.9272 |
| 249° | -0.9336 |
| 250° | -0.9397 |
| 251° | -0.9455 |
| 252° | -0.9511 |
| 253° | -0.9563 |
| 254° | -0.9613 |
| 255° | -0.9659 |
| 256° | -0.9703 |
| 257° | -0.9744 |
| 258° | -0.9781 |
| 259° | -0.9816 |
| 260° | -0.9848 |
| 261° | -0.9877 |
| 262° | -0.9903 |
| 263° | -0.9925 |
| 264° | -0.9945 |
| 265° | -0.9962 |
| 266° | -0.9976 |
| 267° | -0.9986 |
| 268° | -0.9994 |
| 269° | -0.9998 |
| 270° | -1 |
Таблица синусов для углов 181° — 270°
| Угол | Sin (Синус) |
|---|---|
| 271° | -0.9998 |
| 272° | -0.9994 |
| 273° | -0.9986 |
| 274° | -0.9976 |
| 275° | -0.9962 |
| 276° | -0.9945 |
| 277° | -0.9925 |
| 278° | -0.9903 |
| 279° | -0.9877 |
| 280° | -0.9848 |
| 281° | -0.9816 |
| 282° | -0.9781 |
| 283° | -0.9744 |
| 284° | -0.9703 |
| 285° | -0.9659 |
| 286° | -0.9613 |
| 287° | -0.9563 |
| 288° | -0.9511 |
| 289° | -0.9455 |
| 290° | -0.9397 |
| 291° | -0.9336 |
| 292° | -0.9272 |
| 293° | -0.9205 |
| 294° | -0.9135 |
| 295° | -0.9063 |
| 296° | -0.8988 |
| 297° | -0.891 |
| 298° | -0.8829 |
| 299° | -0.8746 |
| 300° | -0.866 |
| 301° | -0.8572 |
| 302° | -0.848 |
| 303° | -0.8387 |
| 304° | -0.829 |
| 305° | -0.8192 |
| 306° | -0.809 |
| 307° | -0.7986 |
| 308° | -0.788 |
| 309° | -0.7771 |
| 310° | -0.766 |
| 311° | -0.7547 |
| 312° | -0.7431 |
| 313° | -0.7314 |
| 314° | -0.7193 |
| 315° | -0.7071 |
| 316° | -0.6947 |
| 317° | -0.682 |
| 318° | -0.6691 |
| 319° | -0.6561 |
| 320° | -0.6428 |
| 321° | -0.6293 |
| 322° | -0.6157 |
| 323° | -0.6018 |
| 324° | -0.5878 |
| 325° | -0.5736 |
| 326° | -0.5592 |
| 327° | -0.5446 |
| 328° | -0.5299 |
| 329° | -0.515 |
| 330° | -0.5 |
| 331° | -0.4848 |
| 332° | -0.4695 |
| 333° | -0.454 |
| 334° | -0.4384 |
| 335° | -0.4226 |
| 336° | -0.4067 |
| 337° | -0.3907 |
| 338° | -0.3746 |
| 339° | -0.3584 |
| 340° | -0.342 |
| 341° | -0.3256 |
| 342° | -0.309 |
| 343° | -0.2924 |
| 344° | -0.2756 |
| 345° | -0.2588 |
| 346° | -0.2419 |
| 347° | -0.225 |
| 348° | -0.2079 |
| 349° | -0.1908 |
| 350° | -0.1736 |
| 351° | -0.1564 |
| 352° | -0.1392 |
| 353° | -0.1219 |
| 354° | -0.1045 |
| 355° | -0.0872 |
| 356° | -0.0698 |
| 357° | -0.0523 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° |
Таблица синусов для углов от 271° до 360°
Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.
Чему равен синус 45? …
— А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071
Источник
Сумма и разность синусов и косинусов: вывод формул, примеры
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
Также представим сами углы в виде суммы полусумм и полуразностей.
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
Вывод формулы суммы косинусов
Вывод формулы разности косинусов
Примеры решения практических задач
Пример 1. Проверка формулы суммы синусов двух углов
Пример 2. Применение формулы разности синусов
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Источник