Как найти скорость через сопротивление воздуха

Как найти скорость через сопротивление воздуха

You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.

  • Forums

  • Homework Help

  • Introductory Physics Homework Help

Velocity with air resistance help


  • Thread starter
    PHK

  • Start date
    Sep 29, 2007

  • Tags

    Air

    Air resistance

    Resistance

    Velocity

  • Sep 29, 2007

  • #1
I need to find the velocity with the following information. V=Vo+AT and A=G-KV

so how would i find what V equals from this: V=Vo+(G-KV)T

Answers and Replies

  • Sep 29, 2007

  • #2
Thats right. Is there something else to the question too? What velocity do you have to find?

  • Sep 29, 2007

  • #3
theres nothing else to the problem. i plugged in G-KV in for A in the first equation but now i have V=Vo+(G-KV)T. and i want to find velocity, but can’t because there is velocity in the equation. so i want to know how to simplify the equation so i get V only on one side.

  • Sep 29, 2007

  • #4
did anyone figure it out yet?

  • Sep 29, 2007

  • #5
did anyone figure it out yet?

V=Vo+(G-KV)T

V = Vo + GT – KVT

V + KVT = Vo + GT

etc…

  • Sep 29, 2007

  • #6
I think this is right:

V=Vo+(G-KV)T = Vo+TG-TKV
V-Vo=TG-TKV
V-Vo+TKV=TG
V+TKV=TG+Vo
V(1+TK)=TG+Vo

V=(TG+Vo)/(1+TK)

[EDIT]oops, looks like learningphysics beat me to it.

  • Sep 30, 2007

  • #7
“Replacement by an equal expression” is a procedure that is used a lot.
( like you replaced the “A” by “G-kV” )
“Multiplication, Distributive” ( Phoenix line 1 ) and
its inverse , “Factoring” (Phoenix line 5) are the basis of proportion.
When you add the negative of some term to both sides
(so that term cancels the original term on that side)
and/or divide both sides by the same factor
(so as to “move the factor to the other side”)
… there’s always more than one path that you can take
notice how Phoenix “undid” in line 4 , what he had done in line 2 …
it is okay to take more steps, so long as you keep the goal in mind.

  • Sep 30, 2007

  • #8
thanks the equation works. i got one question tho. how did you get from this V+TKV=TG+Vo
to this V(1+TK)=TG+Vo?

  • Sep 30, 2007

  • #9
I need to find the velocity with the following information. V=Vo+AT and A=G-KV

so how would i find what V equals from this: V=Vo+(G-KV)T

Where did you get the equation V = Vo + AT? This equation is derived from calculus for the special case of constant acceleration. In your case, the acceleration is changing with speed, and is therefore not constant.

  • Sep 30, 2007

  • #10
thanks the equation works. i got one question tho. how did you get from this V+TKV=TG+Vo
to this V(1+TK)=TG+Vo?

he factored out the V… try multiplying out: V(1+TK)… what do you get?

Suggested for: Velocity with air resistance help

  • Dec 6, 2022
  • May 1, 2022
  • Oct 18, 2022
  • Sep 27, 2021
  • May 16, 2022
  • Aug 19, 2020
  • Feb 1, 2021
  • Apr 8, 2021
  • Nov 29, 2020
  • Jun 7, 2019

  • Forums

  • Homework Help

  • Introductory Physics Homework Help

Источник

Трение между воздухом и другим объектом называется сопротивлением воздуха. Рассмотрим, как определить сопротивление воздуха при падении объекта.

Сопротивление воздуха падающего объекта можно рассчитать, умножив плотность воздуха на коэффициент сопротивления, умноженный на площадь, на два, а затем умножив на скорость.

Сила тяжести и сопротивление воздуха — две силы естественного поля, которые двигают все на Земле. Формула сопротивления воздуха для сферы, доказательство формулы сопротивления воздуха, формула сопротивления воздуха для свободного падения и то, как получить среднее сопротивление воздуха, будут рассмотрены более подробно.

Как рассчитать сопротивление воздуха падающего предмета?

Скорость, площадь и форма объекта, проходящего через воздух, влияют на сопротивление воздуха. Проверим, как оценить сопротивление воздуха падающего предмета.

Чтобы определить, какое сопротивление воздуха будет испытывать падающий предмет, используйте формулу FD = 1 / 2 ρv2CDА. В этом уравнении FD означает перетаскивание, ρ – плотность жидкости, v для относительной скорости объекта относительно жидкости, CD для коэффициента лобового сопротивления и A для площади поперечного сечения.

Задача: Огромный пассажирский самолет летит со скоростью 250.0 метров в секунду. A = 500 квадратных метров крыльев самолета подвергаются ветру. Коэффициент аэродинамического сопротивления CD = 0.024. Плотность воздуха ρ = 0.4500 кг на кубический метр на высоте самолета. Какому сопротивлению воздуха подвергается пассажирский самолет?

Решение: Даны данные,

А = 500 квадратных метров

CD = 0.024

ρ = 0.4500 кг на кубический метр

Сопротивление воздуха падающего предмета определяется выражением

FD = 1/2 ρv2CDA

FD =(0.4500 кг/м3 × 0.025 × 510.0 м2)/2 (250.0 м/с) 2

FD = (0.4500 кг/м3 × 0.025 × 510.0 м2)/2 (62500 м2/s2)

FD = 179296 кг.м/с2

Как рассчитать сопротивление воздуха при движении снаряда?

Объект или частица называется снарядом, а его движение называется движением снаряда. Посмотрим, как можно рассчитать сопротивление воздуха при движении снаряда.

Скорость, ускорение, и перемещение должно быть включено при описании движения снаряда в целом, как описано ниже,

  • По осям x и y мы должны расположить их составные части. Предположим, что все силы, кроме силы тяжести, ничтожны.
  • Компоненты ускорения тогда чрезвычайно прямолинейны, если положительное направление определено как восходящее, ay = -g = – 0.98 м / с.2 (-32 фут/с2).
  • Поскольку гравитация вертикальна,x = 0. аx = 0 указывает, что vx = V0x, или что начальная и конечная скорости в направлении x равны.
  • При этих ограничениях на ускорение и скорость кинематическое уравнение x (t) = x0 + (вx) среднийt для движения в униформе гравитационное поле можно записать через уравнение v2y (т) = v2oy + 2аy (г – г0), куда входят и остальные кинематические уравнения движения с ускорением с постоянным ускорением.
  • Кинематические уравнения движения в однородном гравитационном поле переходят в кинематические уравнения сy = -г, аx = 0.
  • Горизонтальное движение, v0x= Vx, х = х0 + Vxt.
  • Вертикальное движение, у = у0 + ½ (в0y + Vy)т; вy = Voy – гт; у = уo + Voyт – ½ гт2, v2y = V2oy – 2г (у – уo).

Задача: Снаряд взлетает в воздух во время фейерверка под углом 75.00 над горизонтом с начальной скоростью 70.0 м/с. Снаряд рассчитан так, что взрыватель сработает именно тогда, когда он будет на максимальной высоте над землей.

  • а. Рассчитайте высоту взрыва снаряда.
  • б. Через какое время снаряд выстрелит и взорвется?
  • в. Что происходит с горизонтальным положением снаряда при его взрыве?
  • д. Как далеко в целом продвинулся объект от места запуска до самой высокой точки?

Решение: (а) Под «высотой» мы подразумеваем высоту над начальной точкой или высоту. Когда vy = 0 достигается высшая точка любой траектории, известная как вершина. Мы используем следующее уравнение, чтобы получить y, потому что мы знаем начальное местоположение, начальную и конечную скорости и начальное положение:

v2y = V2oy – 2г (у – у0)

Уравнение упрощается тем, что yo и vy оба равны нулю.

0 = в2oy – 2г.

Вычислив y, мы получаем, y = v2oy/ 2г.

Теперь нам нужно выяснить, какова начальная компонента скорости y, или v0y, является. Его можно рассчитать по формуле v0y=v0sin θ, где v0 обозначает начальную скорость 70.0 м/с и θo=75° обозначает начальный угол. Таким образом-

v0y=v0sin θ = (70.0 м/с) sin750 = 67.6 м/с и-

у = (67.6 м/с)2 / 2(9.80 м/с2)

у = 233 м.

Начальная вертикальная скорость и максимальная высота положительны, потому что вверх положительна, а ускорение, вызванное силой тяжести, отрицательно. Снаряд с начальной вертикальной составляющей скорости 67.6 м/с достигнет максимальной высоты 233 м. Также имейте в виду, что максимальная высота зависит только от вертикальной составляющей начальной скорости (без учета сопротивления воздуха).

(b) Существуют различные способы определить, когда снаряд достигает высшей точки, как и во многих физических задачах. Самый простой подход в этой ситуации — использовать vy=v0y -гт. Это уравнение становится vy= 0 на вершине

0 = в0y− гт

или,

т = voy/g = (67.6 м/с) / (9.80 м/с2)

t = 6.90 с.

Другой способ найти время – использовать y = yo + ½ (в0y + Vy) т.

в) Сопротивление воздуха мало, следовательно, ах и ау равны нулю. И, как упоминалось ранее, горизонтальная скорость постоянна. Как показывают уравнения x=x0+vxт, где х0 равно нулю, горизонтальное перемещение равно горизонтальной скорости, умноженной на время. Таким образом,

х = vxt,

Когда vx – компонент x скорости, определяется выражением

vx = V0cosθ = (70.0 м/с) cos75°=18.1 м/с.

Поскольку оба движения имеют одинаковое время t, x равно

х = (18.1 м/с) × 6.90 с = 125 м.

Без сопротивления воздуха горизонтальное движение имеет постоянную скорость. Горизонтальное смещение, наблюдаемое здесь, может помочь предотвратить травму зрителей от падающих пиротехнических фрагментов. Немалую роль при взрыве снаряда играет сопротивление воздуха, и многие осколки падают сразу внизу.

(d) Нахождение размера и направления смещения в самой высокой точке — это все, что здесь требуется, поскольку горизонтальная и вертикальная составляющие смещения уже рассчитаны:

s→ = 125 см + 233 см; |ŝ|=√ (1252 + 2332) = 264 м; Φ = загар -1 (233/125) = 61.8°

Как рассчитать сопротивление воздуха при конечной скорости?

Сопротивление воздуха по величине эквивалентно весу падающего тела с предельной скоростью. Рассмотрим метод расчета сопротивления воздуха при предельной скорости.

  • Используя второй закон Ньютона для падающего объекта в качестве отправной точки, мы можем определить сопротивление воздуха при конечной скорости: Fg + Far = ма.
  • Для определения сопротивления воздуха при заданной скорости используются следующие два типа сопротивления воздуха: Far = – bv альтернативно, Far = – бв2.
  • Для расчета сопротивления воздуха при конечной скорости используется закон Ньютона для определения сопротивления воздуха при конечной скорости, поскольку ускорение равно нулю. мг – бв = 0; мг – бв2 = 0.
  • Чтобы определить сопротивление воздуха при заданной скорости, ответом на задачу о скорости является vT = мг/б. Альтернативой является то, что vT  = √(мг/б).

Если m представляет массу в килограммах, g — квадрат ускорения свободного падения, а b — произвольная величина.

Задача: При падении из состояния покоя объект массой 55 кг испытывает силу сопротивления воздуха, определяемую Far = -15В2. Определить конечную скорость объекта.

Решение: используйте формулу vT = √ (мг/б) для определения конечной скорости силы сопротивления вида Far = -bv2. Добавляя к уравнению, получаем,

vT = √(55) × (9.81)/15)

vT = 5.99 м / с

Как рассчитать коэффициент сопротивления воздуха?

Коэффициент сопротивления изменяется как квадратное отношение относительной скорости объекта. Рассмотрим метод расчета коэффициента сопротивления воздуха.

Коэффициент сопротивления воздуха рассчитывается по уравнению с = Fвоздух /v2. В расчете Фвоздух – силовое сопротивление, а c – силовая постоянная в этом уравнении. Жидкости, обычно вода в спортивной среде, также подвержены силе трения, которая не ограничивается только воздухом.

Сопротивление жидкости, сопротивление воздуха и сопротивление — все это относится к одному и тому же.

Проблема: Если объект движется со скоростью 22 мс-1 столкнуться с сопротивлением воздуха 50 Н, какова постоянная силы?

Решение: Даны данные,

v = 22 мс-1

Fвоздух = 50 Н

Формула для коэффициента сопротивления воздуха:

с = Fвоздух /v2

Замените указанные значения в формуле выше. Затем,

с = 50/(22)2

с = 0.103

Как рассчитать аэродинамическое сопротивление парашюта?

Вес пульсирует на шнуре, когда парашют раскрывается. Рассмотрим, как определить аэродинамическое сопротивление парашюта.

  • Чтобы определить аэродинамическое сопротивление парашюта. Уравнение для силы сопротивления парашюта, также известной как его сила сопротивления ветру, имеет вид F.D = 1 / 2 ρv2CDА. Где, ФD – сила сопротивления, r – плотность воздуха, Cd — коэффициент лобового сопротивления, A — площадь парашюта, а v — скорость в воздухе.
  • Чтобы определить сопротивление воздуха парашюта по квадрату скорости, сопротивление возрастает.
  • Чтобы определить сопротивление воздуха парашюта, нет никакой чистой силы, действующей на ракету, когда сопротивление равно весу. F = D – W = 0.
  • Cd = 2 Фd / ρв2A = W для определения аэродинамического сопротивления парашюта.
  • И, наконец, V = sqrt (2W/Cdρ A) используется для определения аэродинамического сопротивления парашюта.

При сравнении двух предметов те, у которых больший вес, меньший коэффициент лобового сопротивления, меньшая плотность газа или меньшая площадь, движутся с большей скоростью.

Как найти сопротивление воздуха через массу и ускорение?

Единственной силой, воздействующей на людей поначалу, является гравитация, которая толкает их со скоростью -9.8 м/с2. Давайте посмотрим, как можно рассчитать сопротивление воздуха, используя массу и ускорение.

  • Чтобы найти сопротивление воздуха с массой и ускорением, мы можем использовать некоторую алгебру, чтобы получить ускорение объекта с точки зрения чистой внешней силы и массы объекта (a = F/m).
  • Чистая внешняя сила (F = W – D) равна разнице между силами веса и силы сопротивления. Тогда ускорение объекта определяется выражением a = (W – D) / m.

Задача: Автомобиль массой около 29 кг движется из Калькутты в Раджастхан со скоростью 50 метров в секунду, а гусеница нагружена железом и весит 84 кг. Определить силу сопротивления автомобиля.

Решение: Даны данные,

Ускорение = 50 м/с2

Вес = 84 кг

Масса = 29 кг

Мы знаем, что a = (W – D) / m

50 = (84 – Д)/ 29

1450 = 84 – Д

-Д = 1450 – 84

Д = – 1366 Н

График сопротивления воздуха

Когда частички воздуха сталкиваются с передней частью объекта, он замедляется. Давайте проверим этот график сопротивления воздуха.

Кредит изображения – График сопротивления воздуха by Кропоткино 113 (говорить) (CC-BY-SA-3.0)

За счет уменьшения угла выпуска можно свести к минимуму влияние сопротивления воздуха на горизонтальную составляющую траектории снаряда. Расстояние и скорость, или скорость, обратно пропорциональны.

Как рассчитать сопротивление воздуха по скорости?

Чем больше частиц воздуха воздействует на объект, тем больше его общее сопротивление увеличивается с площадью поверхности. Давайте рассмотрим, как определить сопротивление воздуха на основе скорости.

Формула, используемая для определения сопротивления воздуха по скорости: c = Fv.2. Сила сопротивления воздуха представлена ​​в технике буквой F, постоянная силы представлена ​​буквой c, а скорость объекта представлена ​​буквой v. Существует линейная зависимость между сопротивлением воздуха и величиной сопротивления воздуха. плотность.

Между скоростью и сопротивлением воздуха создается квадратичная зависимость. Площадь передней кромки объекта, движущегося по воздуху, определяет, какое сопротивление воздуха он будет испытывать. Сопротивление воздуха увеличивается с увеличением площади.

Задача: Если сопротивление воздуха тела равно 34 Н, а силовая постоянная равна 0.04, какова его скорость?

Данные приведены, Fвоздух = 34 Н и с = 0.04

Формула сопротивления воздуха:

Fвоздух = резюме2

v2 = 34 / 0.04

v2 = 850

v = 29.15 м / с.

Как рассчитать силу сопротивления воздуха?

Сила сопротивления воздуха измеряется в Ньютонах (Н). Рассмотрим, как определить силу сопротивления воздуха.

Fвоздух = – резюме2 уравнение, используемое для определения силы сопротивления воздуха. Фвоздух – силовое сопротивление, а c – силовая постоянная в этом уравнении. Знак минус показывает, что объект движется в направлении, противоположном направлению сопротивления воздуха.

Задача: силовая постоянная для самолета, движущегося со скоростью 50 мс.-1 составляет 0.05. Определить сопротивление воздуха.

Решение: Даны данные,

Скорость воздуха, v = 50

Силовая постоянная, c = 0.05

Сила воздуха определяется выражением

F = – резюме2

F = (-) 0.05 × 50 × 50

F = – 125 Н.

Формула сопротивления воздуха для шара

Зависимость между силой сопротивления, действующей на тело, и сопротивлением воздуха обратная. Давайте посмотрим на формулу сопротивления воздуха шара.

Коэффициент сопротивления воздуха для сферических материалов можно рассчитать по следующей формуле: Cd = 2 Фd / ρв2A, где для сферических материалов-

  • Cd = коэффициент сопротивления воздуха, 
  • Fd сопротивление воздуха по Ньютону, 
  • А – площадь формы в плане в квадратных метрах,
  • ρ = плотность сферы, выраженная в килограммах на кубический метр,
  • А вязкость вещества, выраженная в метрах в секунду, известна как v.

Задача: Плотность воздуха 0.4500 кг/м3, а самолет, летящий на высоте, имеет скорость 250 м/с. 500 м2 Крылья самолета открыты ветру. На самолет действует сила сопротивления воздуха 168750 Н. Выполните расчет коэффициента лобового сопротивления.

Решение: Приведенные данные, Сопротивление воздуха для сферических материалов, Fd = 168750 Н

Плотность, ρ = 0.4500 кг/м3

Площадь поперечного сечения, А = 500 м2

Скорость, v = 250 м/с

Мы знаем, что для сферических материалов

Cd = 2 Фd / ρв2A

Cd = 2 × 168750 / (0.4500 × 2502 × 500)

Cd = 0.025

Как рассчитать среднее сопротивление воздуха?

Сопротивление воздуха — это разновидность жидкостного трения, которое влияет на падающие в воздухе предметы. Давайте посмотрим, как определить среднее сопротивление воздуха.

Умножив плотность воздуха, коэффициент сопротивления, площадь и скорость на два, можно рассчитать среднее сопротивление воздуха, которое будет испытывать падающий объект. Гравитация заставляет объекты двигаться вниз, в отличие от трения воздуха, которое действует противоположным образом и замедляет скорость.

Сопротивление воздуха возрастает по мере увеличения площади поверхности, на которую падают предметы.

Заключение

Сопротивление воздуха – это сила, которую испытывает объект при прохождении через воздух, где, если человек движется быстрее, сила сопротивления воздуха возрастает. Безразмерный коэффициент сопротивления CD, который рассчитывается как CD = ФD/1/2 ρАв2 где ρ — плотность жидкости (в данном случае воздуха). Площадь поперечного сечения объекта A = (1/4) ΠD2, а его скорость v.

Источник

Время на прочтение
3 мин

Количество просмотров 9.6K

Немного теории.

Для начала разберемся с тем, что такое лошадиные силы и устроим небольшой экскурс в школьную физику.

1 л.с. – это мощность, затрачиваемая при вертикальном подъёме груза массой 75 кг со скоростью 1 м/с.

F = mg = 75text{ кг} cdot 9.8text{ Н/кг} = 735 text{ Н} - text{сила тяжести груза}

Как известно, мощность показывает, какую работу совершает тело в единицу времени:

P = dfrac{A}{t}

Работа равна произведению силы на перемещение: A = F*S. Учитывая, что скорость V=S/t, получим:

P = Fcdot dfrac{S}{t} = Fcdot V = 735text{ Н} cdot 1 text{ м/с} = 735 text{ Вт}

Получаем формулу для перевода лошадиных сил в принятую в международной системе СИ единицу измерения мощности – Ватт:

1 text{ л.с.} = 735 text{ Вт}

Перейдем к основной части, а именно – к техническим характеристикам автомобиля.

Некоторые характеристики и расчёты будут приводиться приближенно, поскольку мы не претендуем на умопомрачительную точность расчетов, важнее понять физику и математику процесса.

m = 2 тонны = 2000 кг – масса автомобиля (масса авто 1940 кг, считаем что в ней водитель массой 60 кг и больше ничего/никого).
P = 670 л.с. (по паспорту 625 л.с., но реально мощность выше – измерено на динамометрическом стенде в ролике DSC OFF https://www.youtube.com/watch?v=ysg0Depmyjc. В этой статье мы ещё обратимся к замерам отсюда.)
Разгон 0-100 км/ч: 3.2-3.3 с (по паспорту, замерам)
Разгон 100-200 км/ч: 7.5-7.6 с (по паспорту, замерам)

Мощность двигателя генерируется на маховике, потом через сцепление передается в КПП, далее через дифференциалы, привода, карданный вал передается на колёса. В результате эти механизмы поглощают часть мощности и итоговая мощность, поставляемая к колесам, оказывается меньше на 18-28%. Именно мощность на колесах определяет динамические характеристики автомобиля.

У меня нет сомнений в гениальности инженеров БМВ, но, для начала, возьмем для удобства потери мощности 20%.

Вернемся к нашим физическим баранам. Для вычисления разгона нам нужно связать мощность со скоростью и временем разгона. Для этого воспользуемся вторым законом Ньютона:

F = ma, text{где } F - сила, m - text{масса тела}, \a - text{ускорение, сообщаемое силой } F text{ телу массой }m.\a = (V-V_0)/t - ускорение - text{изменение скорости за время } t.\S = x_0 + V_0cdot t + dfrac{at^2}{2} - text{путь, пройденный телом за время }t, \x_0 - text{начальная координата}, V_0 - text{начальная скорость}, a - ускорение. \ text{Для удобства будем считать }x_0 = 0.text{ Для разгона }0-100 dfrac{км}{ч}: V_0 = 0.

Вооружившись этими знаниями, получим конечную формулу:

P = dfrac{FS}{t}=dfrac{macdot S}{t} = dfrac{ma cdot dfrac{at^2}{2}}{t} = dfrac{ma^2t}{2} = dfrac{mleft(dfrac{V-V_0}{t}right)^2 t}{2}=dfrac{m(Delta V)^2}{2t}

Выражая отсюда t, получим итоговую формулу для вычисления разгона:

t = dfrac{m(Delta V)^2}{2P}

На самом деле в паспорте автомобиля указывается максимальная мощность, достигаемая двигателем при определенном числе оборотов. Ниже приведена зависимость мощности двигателя от числа оборотов (синяя линия). Строго говоря, параметры этой кривой зависят от номера передачи, так что для определенности скажем, что график для 5й передачи.

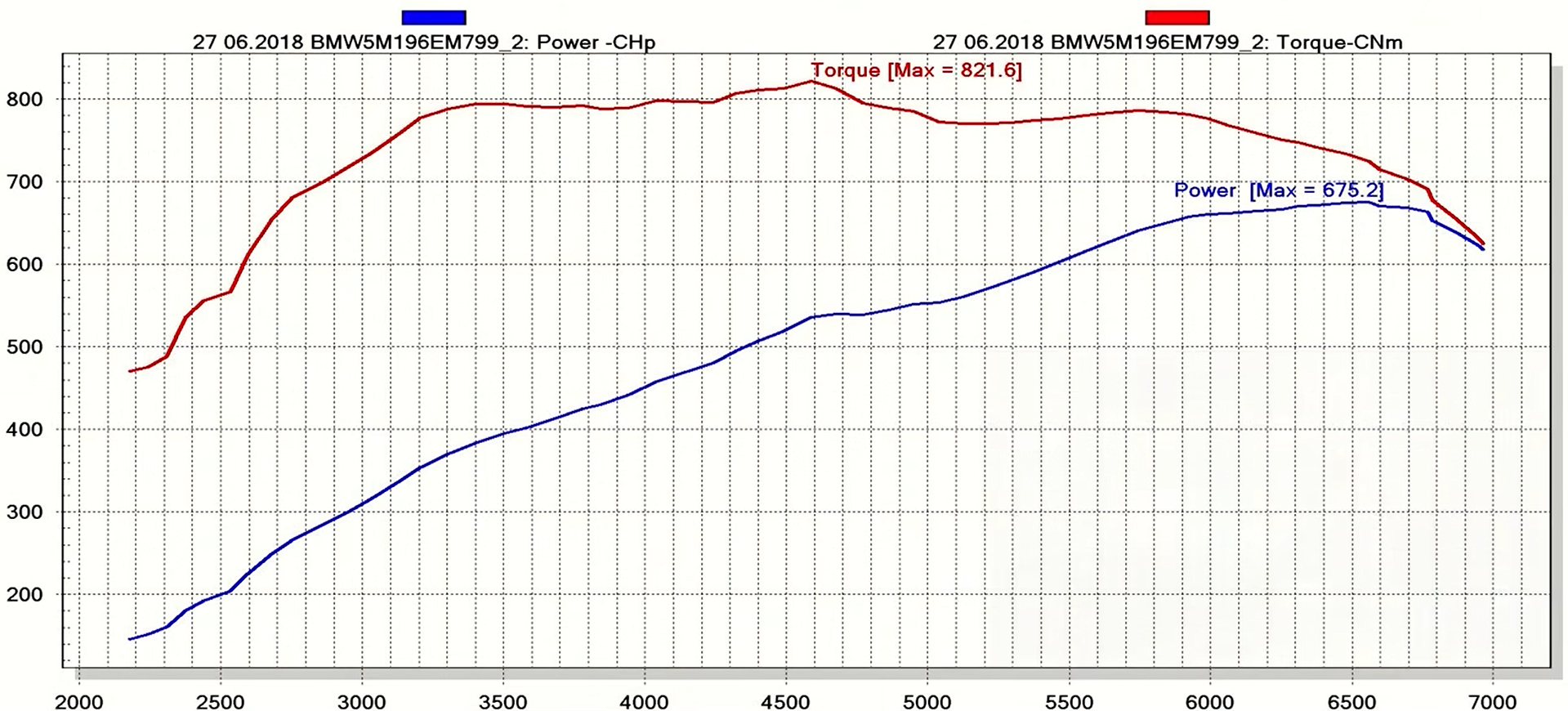
Главное, что мы должны усвоить из этого графика – мощность автомобиля не постоянна во время движения, а увеличивается по мере роста оборотов двигателя.

Перейдем к расчету разгона от 0 до 100 км/ч. Переведем скорость в м/с:

100 dfrac{км}{ч} = 28 dfrac{м}{с}

При разгоне от 0 до 100 км/ч автомобиль практически сразу переключается с первой передачи на вторую, и при достижении около 90 км/ч переключается на третью. Будем считать, что на всём протяжении разгона автомобиль разгоняется на второй передаче, причем максимальная мощность будет меньше 670 л.с., поскольку передача ниже пятой. Возьмём в качестве начальной мощности при 0 км/ч мощность 150 л.с. (при 2000 об/мин), конечную – 600 л.с. (7000 об/мин):

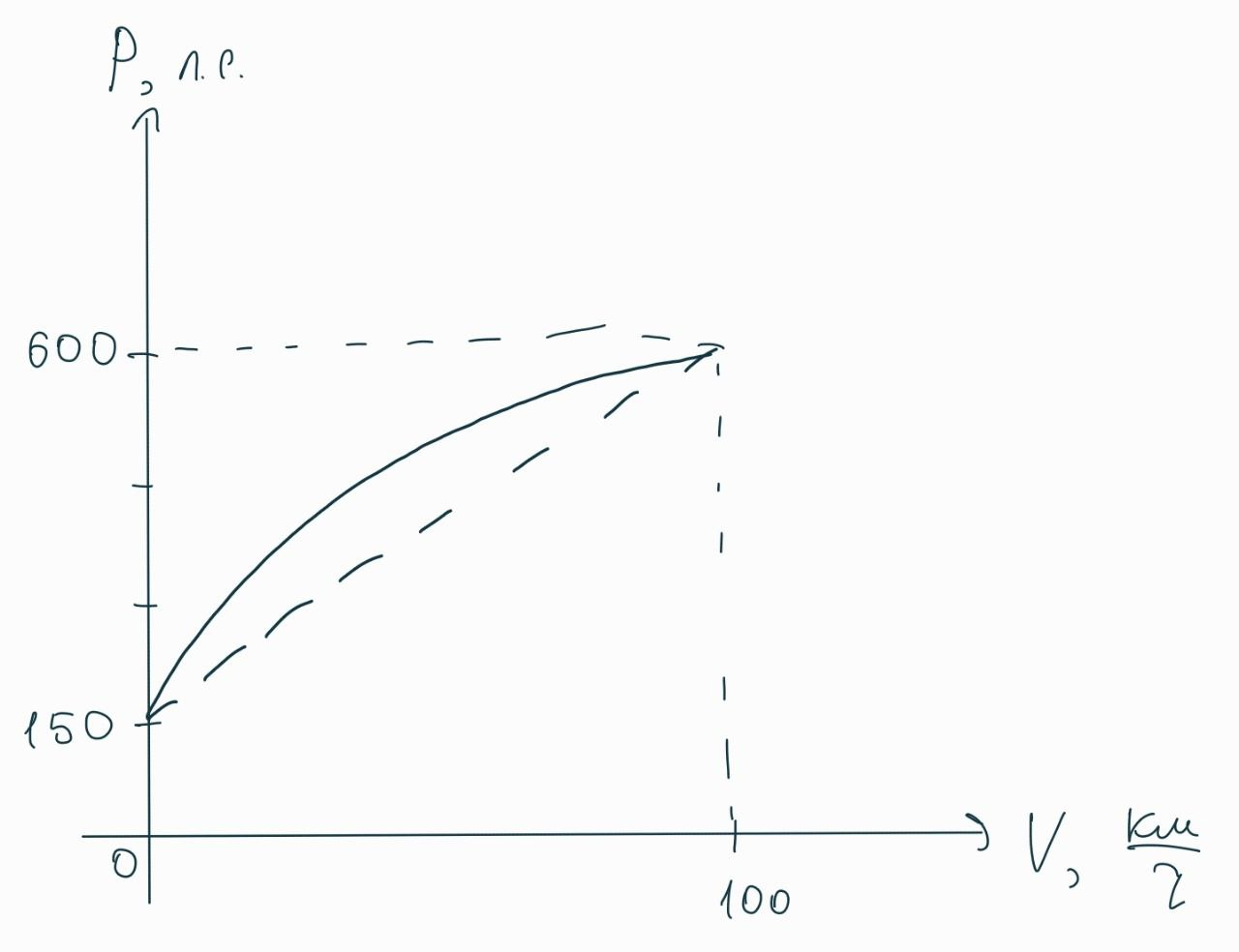
Чтобы не считать сложные интегралы для вычисления средней мощности, скажем следующие слова: учитывая приближенный характер наших расчетов, проскальзывание авто при ускорении, а также сопротивление воздуха (хотя при разгоне от 0 до 100 оно играет не такую большую роль, как при разгоне до 200 км/ч), будем считать, что мощность зависит от скорости линейно, тогда средняя мощность при разгоне от 0 до 100 км/ч составляет:

<P>=dfrac{150+600}{2}=375 text{ л.с.}

Пришло время учесть потери мощности, о которых было сказано ранее, а заодно перевести мощность в кВт (1 кВт = 1000 Вт) для удобства. Потери мощности 20%, значит эффективность 80%=0.8:

P = P_{реальная}=375cdot 735 text{ Вт} cdot 0.8 = 220500 text{ Вт} = 220 text{ кВт}

Теперь подставляем всё в конечную формулу:

t = dfrac{m(Delta V)^2}{2P} = dfrac{2 cdot 10^3 text{ кг}cdot left(28 dfrac{м}{с} right)^2}{2cdot 220 cdot 10^3 text{ Вт}} simeq 3.6 text{ с}

Получили довольно близкий к “паспортным” 3.3 с результат, ура! Специально не стал ничего дополнительно подгонять, дабы подчеркнуть приближенный характер расчёта, хотя это было довольно просто сделать, взяв, например, чуть больше мощность.

Теперь, ради интереса и проверки самих себя, вычислим разгон 100-200 км/ч.

С ростом скорости растёт трение воздуха, для движения используются более высокие передачи КПП (3-я, 4-я, 5-я), но при этом уменьшается проскальзывание колес. Так что оставим среднюю мощность 375 л.с.

Так делать конечно же нельзя! После 2-й передачи двигатель работает на “комфортных” для себя оборотах 4000-7000 об/мин, поэтому средняя мощность будет гораздо выше, поскольку выше будет начальная мощность для каждой передачи. Здесь уже не получится считать, что автомобиль едет только на 4-й передаче на всем протяжении разгона, но можно считать, что он проехал одинаковые промежутки времени на 3-й, 4-й и 5-й передаче, и пусть график зависимости мощности от числа оборотов для них одинаков, поэтому построим общую условную кривую зависимости мощности от скорости:

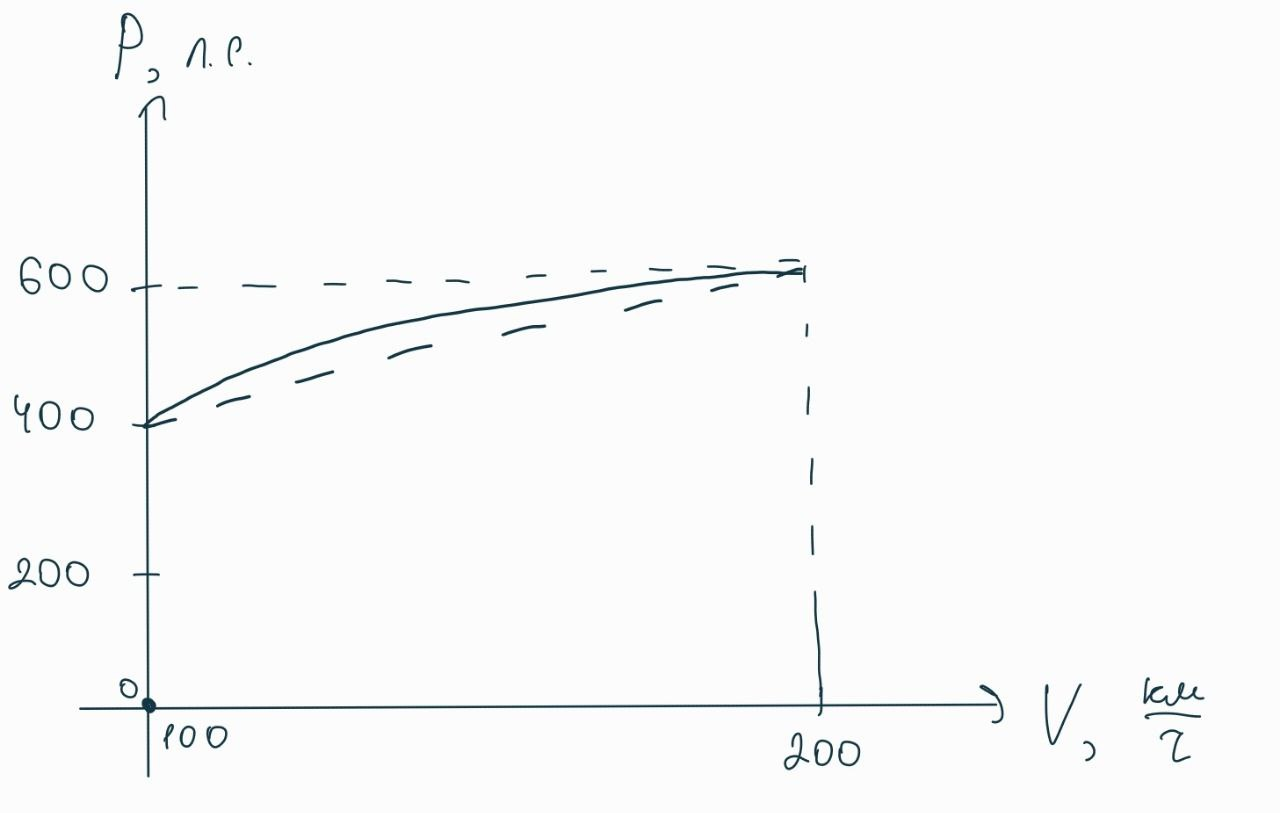
Опять же, считаем для простоты зависимость мощности от скорости линейной, тогда получаем среднюю и реальную мощность:

<P>=dfrac{400+600}{2}=500 text{ л.с.} \P = P_{реальная}=500cdot 735 text{ Вт} cdot 0.8 simeq 300 text{ кВт}

Тогда итоговое время разгона 100-200 км/ч:

t = dfrac{m (V^2 - V_0^2)}{2P} = dfrac{2 cdot 10^3 text{ кг}cdot left[left(56 dfrac{м}{с} right)^2 - left(28 dfrac{м}{с} right)^2 right]}{2cdot 300 cdot 10^3 text{ Вт}} simeq 7.8 text{ с}

Время разгона “по паспорту” 7.6 с. И снова мы оказались близко к истине!

P.S. не хочу объяснять, откуда взялось (V^2 – V_0^2), можете повыводить на досуге 🙂

Ну и в общем-то всё. Приведенные рассуждения и вычисления не претендуют на истину в последней инстанции и большую точность, но показывают, что зная “школьные” формулы по физике, можно решать такие интересные задачки, связанные с жизнью.

Источник

Лекция 7. Уравнение движения автомобиля

План лекции

7.1 Силы сопротивления движению и мощности, затрачиваемые на их преодоление

7. 2. Уравнение движения автомобиля

7. 1 Силы сопротивления движению и мощности, затрачиваемые на их преодоление

Силами сопротивления называются силы, препятствующие Движению автомобиля. Эти силы направлены против его движе­ния.

При движении на подъеме, характеризуемом высотой Нп, длиной проекции Вп на гори­зонтальную плоскость и углом подъема дороги а, на автомобиль действуют следующие силы со­противления (рис. 7.1): сила со­противления качению Рк, равная сумме сил сопротивления каче­нию передних (РК1) и задних (РК2) колес, сила сопротивления подъе­му Рп, сила сопротивления воз­духа Рв и сила сопротивления раз­гону Ри. Силы сопротивления ка­чению и подъему связаны с особенностями дороги. Сумма этих сил называется силой сопротивления дороги Рд.

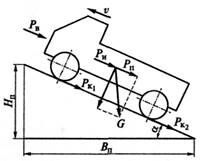
Рис. 7.1. Силы сопротивления движению автомобиля

Сила сопротивления качению

Возникновение силы сопротивления качению при движении обусловлено потерями энергии на внутреннее трение в шинах, поверхностное трение шин о дорогу и образование колеи (на де­формируемых дорогах).

Рекомендуемые материалы

О потерях энергии на внутреннее трение в шине можно судить по рис. 7.2, на котором приведена зависимость между вертикаль­ной нагрузкой на колесо и деформацией шины — ее прогибом fш.

При движении колеса по неровной поверхности шина, испы­тывая действие переменной нагрузки, деформируется. Линия Оа, которая соответствует возрастанию нагрузки, деформирующей шину, не совпадает с линией аО, отвечающей снятию нагрузки. Площадь области, заключенной между указанными кривыми, ха­рактеризует потери энергии на внутреннее трение между отдель­ными частями шины (протектор, каркас, слои корда и др.).

Потери энергии на трение в шине называются гистерезисом, а линия ОаО — петлей гистерезиса.

Потери на трение в шине необратимы, так как при деформа­ции она нагревается и из нее выделяется теплота, которая рассе­ивается в окружающую среду. Энергия, затрачиваемая на дефор­мацию шины, не возвращается полностью при последующем вос­становлении ее формы.

Сила сопротивления качению Рк достигает наибольшего зна­чения при движении по горизонтальной дороге. В этом случае

Рк =fG, где G — вес автомобиля, Н; f — коэффициент сопротивления качению.

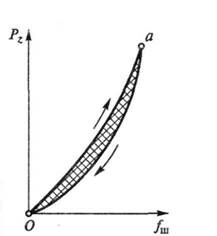
Рис. 7.2. Потери энергии на внутреннее трение в шине:

а — точка, соответствующая мак­симальным значениям нагрузки и прогиба шины

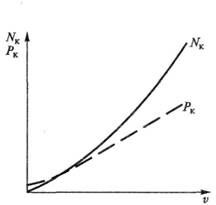
Рис. 7.3. Зависимости силы сопротив­ления качению Рк и мощности NK, не­обходимой для преодоления этого со­противления, от скорости автомобиля

При движении на подъеме и спуске сила сопротивления каче­нию уменьшается по сравнению с Рк на горизонтальной дороге, и тем значительнее, чем они круче. Для этого случая движения сила сопротивления качению

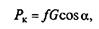
где а — угол подъема, °.

Зная силу сопротивления качению, можно определить мощ­ность, кВт, затрачиваемую на преодоление этого сопротивления:

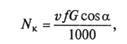
где v — скорость автомобиля, м/с. Для горизонтальной дороги cos 0° = 1 и

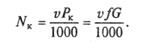
Зависимости силы сопротивления качению Рк и мощности NK от скорости автомобиля v показаны на рис. 7.3.

Коэффициент сопротивления качению

Коэффициент сопротивления качению существенно влияет на потери энергии при движении автомобиля. Он зависит от многих конструктивных и эксплуатационных факторов и определяется экспериментально. Его средние значения для различных дорог при Нормальном давлении воздуха в шине составляют 0,01 …0,1.

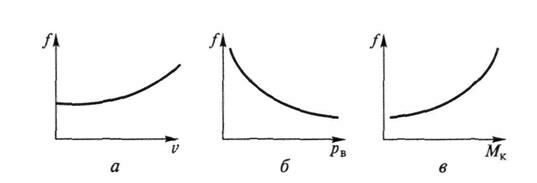
Рис 7.4. Зависимости коэффициента сопротивления качению от

скорости движения (а), давления воздуха в шине (б) и момента,

передаваемого через колесо (в)

Рассмотрим влияние различных факторов на коэффициент со­противления качению.

Скорость движения. При изменении скорости движения в ин­тервале 0…50 км/ч коэффициент сопротивления качению изме­няется незначительно и его можно считать постоянным в указан­ном диапазоне скоростей.

При повышении скорости движения за пределами указанного интервала коэффициент сопротивления качению существенно уве­личивается (рис. 7.4, а) вследствие возрастания потерь энергии в шине на трение.

Коэффициент сопротивления качению в зависимости от ско­рости движения можно приближенно рассчитать по формуле

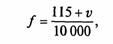
где v — скорость автомобиля, км/ч.

Тип и состояние покрытия дороги. На дорогах с твердым по­крытием сопротивление качению обусловлено главным образом деформациями шины.

При увеличении числа дорожных неровностей коэффициент сопротивления качению возрастает.

На деформируемых дорогах коэффициент сопротивления ка­чению определяется деформациями шины и дороги. В этом случае он зависит не только от типа шины, но и от глубины образую­щейся колеи и состояния грунта.

Значения коэффициента сопротивления качению при рекомен­дуемых уровнях давления воздуха и нагрузки на шину и средней скорости движения на различных дорогах приведены ниже:

Асфальто- и цементобетонное шоссе:

в хорошем состоянии……………………………   0,007…0,015

в удовлетворительном состоянии…………..   0,015…0,02

Гравийная дорога в хорошем состоянии…..    0,02…0,025

Булыжная дорога в хорошем состоянии……   0,025…0,03

Грунтовая дорога сухая, укатанная…………..    0,025…0,03

Песок………………………………………………………        0,1…0,3

Обледенелая дорога, лед………………………….    0,015…0,03

Укатанная снежная дорога……………………….     0,03…0,05

Тип шины. Коэффициент сопротивления качению во многом зависит от рисунка протектора, его износа, конструкции каркаса и качества материала шины. Изношенность протектора, уменьше­ние числа слоев корда и улучшение качества материала приводят к падению коэффициента сопротивления качению вследствие снижения потерь энергии в шине.

Давление воздуха в шине. На дорогах с твердым покрытием при уменьшении давления воздуха в шине коэффициент сопро­тивления качению повышается (рис. 7.4, б). На деформируемых дорогах при снижении давления воздуха в шине уменьшается глу­бина колеи, но возрастают потери на внутреннее трение в шине. Поэтому для каждого типа дороги рекомендуется определенное давление воздуха в шине, при котором коэффициент сопротивле­ния качению имеет минимальное значение.

Нагрузка на колесо. При увеличении вертикальной нагрузки на колесо коэффициент сопротивления качению существенно возрастает на деформируемых дорогах и незначительно — на до­рогах с твердым покрытием.

Момент, передаваемый через колесо. При передаче момента через колесо коэффициент сопротивления качению возрастает (рис. 7.4, в) вследствие потерь на проскальзывание шины в месте ее контакта с дорогой. Для ведущих колес значение коэффициента сопротивления качению на 10… 15 % больше, чем для ведомых.

Коэффициент сопротивления качению оказывает существен­ное влияние на расход топлива и, следовательно, на топливную экономичность автомобиля. Исследования показали, что даже не­большое уменьшение этого коэффициента обеспечивает ощути­мую экономию топлива. Поэтому неслучайно стремление конст­рукторов и исследователей создать такие шины, при использова­нии которых коэффициент сопротивления качению будет незна­чительным, но это весьма сложная проблема.

Сила сопротивления подъему

Вес автомобиля, который движется на подъеме, можно разло­жить на две составляющие (см. рис. 7.1): параллельную и перпен­дикулярную поверхности дороги. Составляющая силы тяжести, параллельная поверхности дороги, представляет собой силу со­противления подъему, Н:

Рп = Gsinα,

где G — вес автомобиля, Н; a — угол подъема, °.

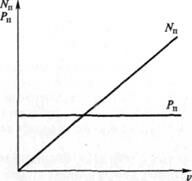
Рис. 7.5. Зависимости силы сопро­тивления подъему Рп и мощности Nп, необходимой для его преодоле­ния, от скорости автомобиля

В качестве характеристики кру­тизны подъема наряду с углом α используют величину i, называе­мую уклоном и равную i = H/Bn, где Нп — высота подъема; Bn — длина его проекции на горизон­тальную плоскость. Сила сопротивления подъему может быть направлена как в сто­рону движения, так и против него. В процессе подъема она дей­ствует в направлении, противоположном движению, и является силой сопротивления движению. При спуске эта сила, направлен­ная в сторону движения, становится движущей.

Зная силу сопротивления подъему, можно определить мощ­ность, кВт, необходимую для преодоления этого сопротивления:

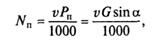
где v — скорость автомобиля, м/с.

Зависимости силы сопротивления подъему Рп „ и мощности Nn, необходимой для преодоления этого сопротивления, от скорости автомобиля v приведены на рис. 7.5.

Сила сопротивления дороги

Сила сопротивления дороги представляет собой сумму сил со­противления качению и сопротивления подъему:

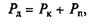
или

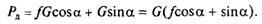
Выражение в скобках, характеризующее дорогу в общем слу­чае, называется коэффициентом сопротивления дороги:

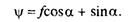
При малых углах подъема (не превышающих 5°), характерных для большинства автомобильных дорог с твердым покрытием, ко­эффициент сопротивления дороги

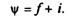
Сила сопротивления дороги в этом случае

Рд =ψG

Зная силу сопротивления доро­ги, можно определить мощность, кВт, необходимую для его преодо­ления:

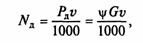
где скорость автомобиля v выражена в м/с, вес G — в Н, мощ­ность NД — в кВт.

Зависимости силы сопротивления дороги Рв и мощности NД, затрачиваемой на его преодоление, от скорости автомобиля v представлены на рис. 7.6.

Сила сопротивления воздуха

При движении действие силы сопротивления воздуха обуслов­лено перемещением частиц воздуха и их трением о поверхность автомобиля. Если он движется при отсутствии ветра, то сила со­противления воздуха, Н:

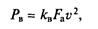
тогда как при наличии ветра

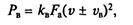
где kв — коэффициент сопротивления воздуха (коэффициент об­текаемости), Н-с2/м4; Fa — лобовая площадь автомобиля, м2; v — скорость автомобиля, м/с; vB — скорость ветра, м/с (знак «+» со­ответствует встречному ветру, знак «-» — попутному).

Коэффициент сопротивления воздуха, зависящий от формы и качества поверхности автомобиля, определяется эксперимен­тально при продувке в аэродинамической трубе.

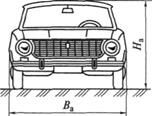
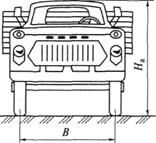
Рис. 7.7. Площади лобового сопротивления легкового (а) и грузового

(б) автомобилей

Коэффициент сопротивления воздуха, Н-с2/м4, составляет 0,2…0,35 для легковых автомобилей, 0,35…0,4 — для автобусов и 0,6…0,7 — для грузовых автомобилей. При наличии прицепов со­противление воздуха увеличивается, так как возрастает наружная поверхность трения и возникают завихрения воздуха между тягачом и прицепами. При этом каждый прицеп вызывает увеличение коэффициента kв в среднем на 15…25 %.

Лобовая площадь автомобиля зависит от его типа (рис. 7.7). Ее приближенное значение, м2, можно вычислить по следующим фор­мулам:

FA = ВНа — для грузовых автомобилей и автобусов;

Fa = 0,78ВаНа — для легковых автомобилей,

где В — колея колес автомобиля, м; На — наибольшая высота автомобиля, м; Bа — наибольшая ширина автомобиля, м.

Мощность, кВт, затрачиваемая на преодоление сопротивле­ния воздуха:

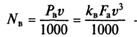 — при отсутствии ветра;

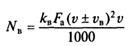 — при наличии ветра.

Зависимости силы сопротивления воздуха Рв и мощности NB, необхо­димой для преодоления этого сопро­тивления, от скорости автомобиля v приведены на рис. 7.8.

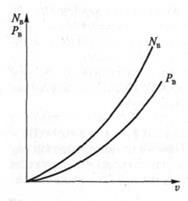
Рис. 7.8. Зависимости силы сопротивле­ния воздуха Рв и мощности Nb, необхо­димой для преодоления этого сопротив­ления, от скорости автомобиля

Сила сопротивления разгону

Сила сопротивления разгону воз­никает вследствие затрат энергии на раскручивание вращающихся частей двигателя и трансмиссии, а также колес при движении автомобиля с ускорением.

Сила сопротивления разгону, Н:

=

где G — вес автомобиля, Н; g — ус­корение силы тяжести, м/с2; 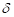вр — коэффициент учета вращающихся масс автомобиля; j — ускорение ав­томобиля, м/с2.

Мощность, кВт, затрачиваемая на разгон:

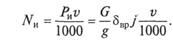
Зависимости силы сопротивления разгону Ри и мощности NK, необходимой для преодоления этого сопротивления, от скорости автомобиля v представлены на рис. 7.9.

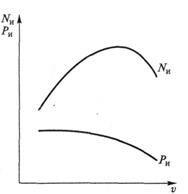
Рис. 7.9. Зависимости силы сопротивления разгону Ря и мощности /Уи, необходимой для преодоления этого сопро­тивления, от скорости авто­мобиля

Коэффициент учета вращающихся масс

Этот коэффициент учитывает дополнительное сопротивление разгону автомобиля, вызванное раскручиванием вращающихся ча­стей двигателя, трансмиссии и колес.

Коэффициент учета вращающихся масс показывает, во сколь­ко раз мощность, затрачиваемая на разгон автомобиля, больше мощности, необходимой для установившегося движения:

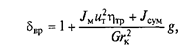
где JM — момент инерции маховика; uТ, 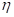Чтр — передаточное число и КПД трансмиссии; Jсум — суммарный момент инерции всех ко­лес автомобиля.

Коэффициент учета вращающихся масс для автомобиля с пол­ной нагрузкой можно приближенно рассчитать по формуле

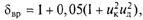
где ик, ид — передаточные числа основной и дополнительной ко­робок передач.

7.2. Уравнение движения автомобиля

Для вывода уравнения движения рассмотрим разгон автомоби­ля на подъеме (рис. 7.10).

Спроецируем все силы, действующие на автомобиль, на по­верхность дороги:

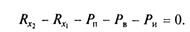(7.1)

Подставим в формулу (7.1) касательные реакции дороги RX1 и RX2, объединим члены с коэффициентом сопротивления каче­нию f и члены с ускорением j и, принимая во внимание соотно­шения f(RZl + RZ2)- Pk и /*, + Л2 = Jк , а также коэффициент уче­та вращающихся масс, получим уравнение движения автомобиля в общем виде:

или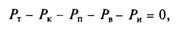

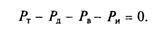(7.2)

Уравнение движения автомобиля выражает связь между дви­жущими силами и силами сопротивления движению. Оно позво­ляет определить режим движения автомобиля в любой момент.

Так, например, при установившемся (равномерном) движе­нии

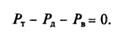
Из уравнения (7.2) следует, что безостановочное движение автомобиля возможно только при условии

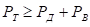
Ещё посмотрите лекцию “18 Дизайн молекул лекарств” по этой теме.

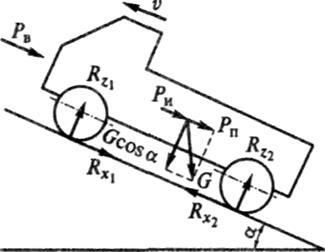
Рис. 7.10. Схема сил, действую­щих на автомобиль на подъеме

данное неравенство связыва­ет конструктивные параметры ав­томобиля с эксплуатационными факторами, обусловливающими сопротивление движению. Одна­ко оно не гарантирует отсутствия буксования ведущих колес. Безо­становочное движение автомоби­ля без буксования ведущих колес возможно лишь при соблюдении условия

Рсц 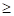 РТ 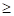 РД + РВ.

Условие равномерного движения при отсутствии буксования ведущих колес записывается в виде

Рсц 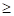 РТ = РД + РВ

Источник

ИНЖЕНЕРНАЯ ПОМОЩЬ

Расчет скорости воздуха в воздуховоде

Расход воздуха L м3/ч
Скорость воздуха
* Скорости в данном диапазоне будут подсвечены 		v1 м/с
v2 м/с

* Сопротивление воздуховода можно посмотреть кликнув по выбранной скорости в таблице

Расчет расхода от скорости L=f(v)

Скорость воздуха в воздуховоде круглого сечения
Ø, мм Ø100 Ø125 Ø160 Ø200 Ø250 Ø280 Ø315 Ø355 Ø400 Ø450 Ø500 Ø560 Ø630 Ø710 Ø800 Ø900 Ø1000 Ø1120 Ø1250 Ø1400 Ø1600 Ø1800 Ø2000
v, м/с
Скорость воздуха в воздуховоде прямоугольного сечения

Источник

Добавить комментарий