Закон Ома назван в честь своего открывателя это ученый Георг Симон Ом. Свои эксперименты в области электричества он начал вдохновляясь опытами Фурье. Ом проводил свои опыты с различными материалами и изучение их электропроводности. Так была разработана знаменитая формула, которая стала краеугольной в современной физике, которая вошла в школьные учебники: I=U/R. Сила тока пропорциональна величине напряжения и имеет обратную пропорциональность сопротивлению.
В статье подробно разобраны области теории и практического применения принципов закона Ома в современной электротехнике. В качестве дополнения, в материале содержатся два обучающих видеоролика и один научный материал на тему статьи.
Закон Ома
Закон Ома показывает отношения между напряжением (U), током (I) и сопротивлением (R). Записано это может быть тремя разными способами:
U = I × R
или
I = V/R
или
R = V/I
Где:
- V – напряжение в вольтах (В);
- I – сила тока в амперах (А);
- R – сопротивление в омах (Ом);
Для большинства схем амперы – слишком большие величины, а омы – слишком маленькие. Поэтому в формулу можно подставлять миллиамперы и килоомы. Если силу тока подставлять в миллиамперах (мА), то сопротивление обязательно должно быть в килоомах (кОм) и наоборот. Напряжение – всегда в вольтах.
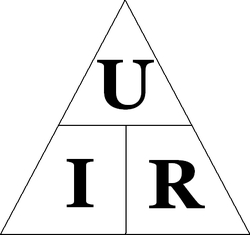
Чтобы проще запомнить три разные версии определения Закона Ома, можно воспользоваться «VIR-треугольником».
- Если надо вычислить напряжение, закрываем пальцем V. У нас остаются I и R. Они на одном уровне, значит между ними ставим знак умножения. Получается: V = I × R .
- Если вычисляем ток, закрываем пальцем I. У нас остаётся V над R. Значит напряжение делится на сопротивление: I = V/R .
- Аналогичным образом поступаем при вычислении сопротивления. Закрываем R. Остаётся V над I. Значит: R = V/I .
Закон Ома, определение: Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Есть также частный случай – Закон Ома для участка цепи – сила тока в участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка.
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Для переменного тока
Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
Для замкнутой цепи
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера применения
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1= I2 ;
- U = U1+ U2 ;
- R = R1+ R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1+ I2 … ;
- U = U1= U2 … ;
- 1 / R = 1 / R1+ 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Друзья, не забывайте подписываться на обновления блога, ведь чем больше читателей подписано на обновления, тем больше я понимаю что делаю что-то важное и полезное и это чертовски мотивирует на новые статьи и материалы.
Закон Ома
Закон Ома — главный закон электротехники, который открыл в 1826 году выдающийся немецкий ученый Георг Симон Ом. Вместе с экспертом разберем формулировку, формулу и задачи на закон Ома с решением

Физика — наука эмпирическая. Ее основные законы вытекают из практического опыта и частенько много лет не имеют теоретических обоснований. Именно так обстоит дело с главным законом электротехники, который открыл в 1826 году выдающийся немецкий ученый Георг Симон Ом.
Электрические явления люди наблюдали сотни лет. Но никак не связывали между собой заряженность потертого янтаря и молнию. Только на исходе XVIII столетия электричество стали внимательно исследовать. В 1795 году Алессандро Вольта изобрел «вольтов столб», химическую батарею, и обнаружил появление тока в проводнике, соединяющем ее полюса. Сферы применения электричества стремительно множились, и появилась острая необходимость в расчетных формулах для инженеров. Эту задачу решали многие ученые, но первым сформулировал главную формулу электротехники именно Георг Ом. Он ввел в обиход понятие сопротивления и опытным путем установил зависимость между основными характеристиками электрической цепи.
Определение закона Ома простыми словами
Электрическая цепь состоит из двухполюсного источника напряжения, то есть батареи, аккумулятора или генератора. Если полюса источника соединить проводами, то по ним потечет электрический ток. Его величина определяется сопротивлением проводников. Наглядное представление этой зависимости — обыкновенный водопровод. Аналогом источника напряжения является насос или водонапорная башня, создающая давление в магистрали, количество воды, прошедшее по трубе, — подобие силы тока, а кран соответствует сопротивлению. Полностью открытый, он не ограничивает поток, по мере закручивания отверстие для воды уменьшается, пока не закроется совсем.
Закон Ома для участка цепи
Опытным путем исследователь установил взаимосвязь характеристик электрической цепи. Классическая формулировка закона Ома звучит так:
«Сила тока на участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению».
Формула закона Ома для участка цепи

В таком виде закон Ома приведен в школьных учебниках физики. Согласно этой простой формуле, для определения уровня тока в проводнике достаточно величину напряжения на его сторонах разделить на некий условно постоянный коэффициент, то есть на сопротивление. Почему «условно»? Потому что величина сопротивления может меняться в зависимости от температуры. Поэтому, кстати, лампы накаливания чаще всего перегорают при включении. Сопротивление холодной спирали ниже, чем нагретой, скачок тока при подаче напряжения вызывает ее резкое расширение и разрыв. Но если этот момент преодолен и нить накала уцелела, то ее сопротивление растет, и ток ограничивается. А при температуре жидкого гелия, например, сопротивление падает до нуля, наступает сверхпроводимость.
Закон Ома для замкнутой полной цепи
Предыдущая формулировка годится только для участка цепи, где отсутствует сам источник электродвижущей силы. В реальности ток течет по замкнутому контуру, где обязательно есть батарея или генератор, имеющий собственное внутреннее сопротивление. Поэтому формула закона Ома для полной цепи выглядит несколько сложнее
Формула закона Ома для замкнутой полной цепи

Применение закона Ома
Георг Ом дал в руки инженеров средство для решения задач, связанных с электрическими цепями. Тепловые и световые приборы, электродвигатели, генераторы, линии электропередач, кабели связи рассчитываются на основе этой простой формулы. Нет такой области электротехники, где она не находит применения. Даже в радиотехнике используется закон Ома, но в дифференциальной форме. «Все гениальное — просто», как считали Еврипид, Леонардо да Винчи, Наполеон Бонапарт и Альберт Эйнштейн, несомненные гении. Закон Ома целиком и полностью подтверждает эту истину.
Сила трения
Единицы измерения силы трения, от чего она зависит и какие виды существуют
подробнее

Задача на закон Ома с решением
Задача для участка электрической цепи
Электрочайник, включенный в сеть с напряжением 220 В, потребляет ток 1,1 А. Каково сопротивление электрочайника.
Дано:
U = 220 В
I = 1,1 А
Решение:
Согласно закону Ома для участка цепи:
R=U/I=220/1,1=200 Ом
Ответ: R = 200 Ом.
Задача для полной замкнутой цепи
Источник постоянного тока с ЭДС E = 24 В и внутренним сопротивлением r = 1,5 Ом замкнут на внешнее сопротивление R = 11 Ом. Определить силу тока в цепи.
Дано:
Е=24 В, r=1,5 Ом, R = 11 Ом
Решение:
По закону Ома для замкнутой цепи: I = E/(R + r) = 24/(11+1,5) = 1,92 А.
Ответ: I=1, 92 А.
Популярные вопросы и ответы
Отвечает Николай Герасимов, старший преподаватель физики в Домашней школе «ИнтернетУрок».
Сколько всего законов Ома в физике?
Существует два закона Ома: закон Ома для участка цепи и закон Ома для полной (замкнутой) цепи. Первый связывает сопротивление участка, силу тока в нём и разность потенциалов (напряжение) на его концах. Кроме того, в нем отражено наличие в цепи источника тока.
Второй учитывает и потребителей электрического тока (электрические лампы, обогреватели, телевизоры и так далее), и его источники (генераторы, батарейки, аккумуляторы). Дело в том, что любой источник тока обладает внутренним сопротивление, которое влияет на силу тока. Именно это и учитывается в законе Ома для полной (замкнутой) цепи.
При каких условиях выполняется закон Ома?
Согласно закону Ома, существует линейная зависимость между силой тока в участке цепи и напряжением на его концах. Он отлично выполняется для металлических проводников при любых напряжениях, а вот для тока в вакууме, газе, растворах или расплавах электролитов, полупроводниках линейная зависимость нарушается, и применять закон Ома в том виде, в котором его изучают в школьном курсе, уже нельзя.
Для чего нужен закон Ома?
Трудно переоценить значимость этого закона. Он позволил производить расчет электрических цепей, без которых практически невозможно представить жизнь современного человека, так как они лежат в основе любого электроприбора, начиная от обычной лампы накаливания и заканчивая самыми современными компьютерами.
В каком классе проходят закон Ома?
В школьном курсе ученики впервые знакомятся с электрическими явлениями и законом Ома для участка цепи в 8 классе. Более подробно о причинах возникновения электрического тока и его источниках ученики знакомятся в курсе старшей школы (10 или 11 класс, в зависимости от программы). Здесь же ученики впервые встречаются и с законом Ома для полной (замкнутой) цепи.
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
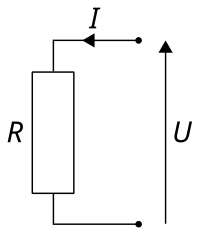
U — напряжение,
I — сила тока,
R — сопротивление
Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника (или электрического напряжения) с силой тока, протекающего в проводнике, и сопротивлением проводника. Установлен Георгом Омом в 1826 году (опубликован в 1827 году) и назван в его честь.
В своей работе[1] Ом записал закон в следующем виде:
где:
- X — показания гальванометра (в современных обозначениях, сила тока I);
- a — величина, характеризующая свойства источника напряжения, постоянная в широких пределах и не зависящая от величины тока (в современной терминологии, электродвижущая сила (ЭДС) ε);
- l — величина, определяемая длиной соединяющих проводов (в современных представлениях соответствует сопротивлению внешней цепи R);
- b — параметр, характеризующий свойства всей электрической установки (в современных представлениях, параметр, в котором можно усмотреть учёт внутреннего сопротивления источника тока r).
Формула (1) при использовании современных терминов выражает закон Ома для полной цепи:
где:
Из закона Ома для полной цепи вытекают следующие следствия:
Часто[2] выражение
где 
Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.
К другой записи формулы (3), а именно:
применима другая формулировка:
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.
Выражение (5) можно переписать в виде
где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный ом» — Мо[3], в Международной системе единиц (СИ) единицей измерения проводимости является си́менс (русское обозначение: См; международное: S), величина которого равна обратному ому.
Мнемоническая диаграмма для закона Ома

Схема, иллюстрирующая три составляющие закона Ома
Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

В соответствии с этой диаграммой формально может быть записано выражение:
которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.
В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:
где:
— удельное электрическое сопротивление материала, из которого сделан проводник,
— его длина
— площадь его поперечного сечения
Закон Ома и ЛЭП
Одним из важнейших требований к линиям электропередачи (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами, задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока 




В таком случае потери мощности будут определяться выражением
Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, желательно всемерное увеличение ЭДС. Однако ЭДС ограничивается электрической прочностью обмотки генератора, поэтому повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в линии возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее практически используемое напряжение в дальних ЛЭП обычно не превышает миллиона вольт.
Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.
Закон Ома в дифференциальной форме
Сопротивление 
Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
где:
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость 
Раздел физики, изучающий течение электрического тока (и другие электромагнитные явления) в различных средах, называется электродинамикой сплошных сред.
Закон Ома для переменного тока
Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновременности достижения напряжением и током своих максимальных значений, то есть учёт фазового сдвига.
Если ток является синусоидальным с циклической частотой ω, а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:
где:
При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, 



Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо. Нелинейность цепи приводит к возникновению гармоник (колебаний с частотой, кратной частоте тока, действующего на цепь), а также колебаний с суммарными и разностными частотами. Вследствие этого закон Ома в нелинейных цепях, вообще говоря, не выполняется.
Трактовка и пределы применимости закона Ома
Закон Ома, в отличие от, например, закона Кулона, является не фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников в приближении небольших частот, плотностей тока и напряжённостей электрического поля, но перестающим соблюдаться в ряде ситуаций.
В классическом приближении закон Ома можно вывести при помощи теории Друде:
Здесь:
Проводники и элементы, для которых соблюдается закон Ома, называются омическими.
Закон Ома может не соблюдаться:
- При высоких частотах, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
- При низких температурах для веществ, обладающих сверхпроводимостью.
- При заметном нагреве проводника проходящим током, в результате чего зависимость напряжения от тока (вольт-амперная характеристика) приобретает нелинейный характер. Классическим примером такого элемента является лампа накаливания.
- При приложении к проводнику или диэлектрику (например, воздуху или изоляционной оболочке) высокого напряжения, вследствие чего возникает пробой.
- В вакуумных и газонаполненных электронных лампах (в том числе люминесцентных).
- В гетерогенных полупроводниках и полупроводниковых приборах, имеющих p-n-переходы, например, в диодах и транзисторах.
- В контактах металл-диэлектрик (вследствие образования пространственного заряда в диэлектрике)[4].
Примечания
- ↑ G. S. Ohm (1827). Die galvanische Kette, mathematisch bearbeitet. Berlin: T. H. Riemann. Архивная копия от 15 марта 2017 на Wayback Machine
- ↑ Преимущественно в школьных учебниках и научно-популярной литературе.
- ↑ Мо / 39422 // Большой энциклопедический словарь / Гл. ред. А. М. Прохоров. — 1-е изд. — М. : Большая российская энциклопедия, 1991. — ISBN 5-85270-160-2.
- ↑ Рез И. С., Поплавко Ю. М. Диэлектрики. Основные свойства и применения в электронике. — М., Радио и связь, 1989, — с. 46-51
Ссылки
- Закон Ома // Элементы.ru. Природа науки, Энциклопедия

{I = dfrac{U}{R}}
На этой странице вы можете рассчитать силу тока, напряжение и сопротивление по закону Ома для участка цепи с помощью удобного калькулятора онлайн
Закон Ома – один из фундаментальных законов электродинамики, который определяет взаимосвязь между напряжением, сопротивлением и силой тока. Он был открыт эмпирическим путем Георгом Омом в 1826 году.
Содержание:
- калькулятор закона Ома
- закон Ома для участка цепи
- формула силы тока
- формула напряжения
- формула сопротивления
- примеры задач
Закон Ома для участка цепи
Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению участка цепи I= dfrac{U}{R}
Формула силы тока
Формула позволяет найти силу тока I через напряжение U и сопротивление R по закону Ома для участка цепи.
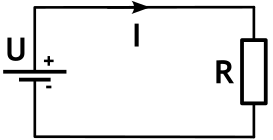
{I = dfrac{U}{R}}
I – сила тока
U – напряжение
R – сопротивление
Сила тока (I) в проводнике прямо пропорциональна напряжению (U) на его концах и обратно пропорциональна его сопротивлению (R).
Формула напряжения
Формула позволяет найти напряжение U через силу тока I и сопротивление R по закону Ома для участка цепи.

{U = I cdot R}
U – напряжение
I – сила тока
R – сопротивление
Падение напряжение на проводнике равно произведению сопротивления проводника на силу тока в нем.
Формула сопротивления
Формула позволяет найти сопротивление R через силу тока I и напряжение U по закону Ома для участка цепи.

{R = dfrac{U}{I}}
R – сопротивление
U – напряжение
I – сила тока
Сопротивление проводника прямо пропорционально напряжению на его концах и обратно пропорционально величине силы тока, протекающего через него.
Примеры задач на нахождение силы тока, напряжения и сопротивления по закону Ома
Задача 1
Найдите силу тока в участке цепи, если его сопротивление 40 Ом, а напряжение на его концах 4 В.
Решение
Воспользуемся формулой силы тока. Подставим в нее значения напряжения и сопротивления, после чего останется произвести простейший математический расчет.
I = dfrac{U}{R} = dfrac{4}{40} = 0.1 А
Ответ: 0.1 А
На этой странице есть калькулятор, который поможет проверить полученный ответ.
Задача 2
Найдите напряжение на концах нагревательного элемента, если его сопротивление 40 Ом, а сила тока 2А.
Решение
Для решения этой задачи нам пригодится формула напряжения.
U = I cdot R = 2 cdot 40 = 80 В
Ответ: 80 В
Проверим получившийся результат с помощью калькулятора .
Задача 3
Найдите сопротивление спирали, сила тока в которой 0.5 А, а напряжение на ее концах 120 В.
Решение
Чтобы найти сопротивление спирали нам потребуется формула сопротивления.
R = dfrac{U}{I} = dfrac{120}{0.5} = 240 Ом
Ответ: 240 Ом
Проверка .
Загрузить PDF
Загрузить PDF
Полное сопротивление, или импеданс, характеризует сопротивление цепи переменному электрическому току. Данная величина измеряется в омах. Для вычисления полного сопротивления цепи необходимо знать значения всех активных сопротивлений (резисторов) и импеданс всех катушек индуктивности и конденсаторов, входящих в данную цепь, причем их величины меняются в зависимости от того, как меняется проходящий через цепь ток. Импеданс можно рассчитать при помощи простой формулы.
Формулы
- Полное сопротивление Z = R или XLили XC (если присутствует что-то одно)
- Полное сопротивление (последовательное соединение) Z = √(R2 + X2) (если присутствуют R и один тип X)
- Полное сопротивление (последовательное соединение) Z = √(R2 + (|XL – XC|)2) (если присутствуют R, XL, XC)
- Полное сопротивление (любое соединение) = R + jX (j — мнимое число √(-1))
- Сопротивление R = I / ΔV
- Индуктивное сопротивление XL = 2πƒL = ωL
- Емкостное сопротивление XC = 1 / 2πƒL = 1 / ωL
-

1
Импеданс обозначается символом Z и измеряется в омах (Ом). Вы можете измерить импеданс электрической цепи или отдельного элемента. Импеданс характеризует сопротивление цепи переменному электрическому току. Есть два типа сопротивления, которые вносят вклад в импеданс:[1]
- Активное сопротивление (R) зависит от материала и формы элемента. Наибольшим активным сопротивлением обладают резисторы, но и другие элементы цепи обладают небольшим активным сопротивлением.
- Реактивное сопротивление (X) зависит от величины электромагнитного поля. Наибольшим реактивным сопротивлением обладают катушки индуктивности и конденсаторы.
-

2
Сопротивление — это фундаментальная физическая величина, описываемая законом Ома: ΔV = I * R.[2]
Эта формула позволит вам вычислить любую из трех величин, если вы знаете две другие. Например, чтобы вычислить сопротивление, перепишите формулу так: R = I / ΔV. Вы также можете измерить сопротивление при помощи мультиметра.- ΔV — это напряжение (разность потенциалов), измеряемое в вольтах (В).
- I — сила тока, измеряемая в амперах (А).
- R — это сопротивление, измеряемое в омах (Ом).
-

3
Реактивное сопротивление имеет место только в цепях переменного тока. Как и активное сопротивление, реактивное сопротивление измеряется в омах (Ом). Есть два типа реактивного сопротивления:
- Индуктивным сопротивлением XC обладают катушки индуктивности, создающие магнитное поле, которое препятствует изменению направления тока в цепи.[3]
Чем быстрее меняется направление тока, тем больше индуктивное сопротивление. - Емкостным сопротивлением XC обладают конденсаторы, которые накапливают электрический заряд. При изменении направления тока в цепи конденсатор неоднократно обнуляет и накапливает электрический заряд. Чем дольше конденсатор заряжается, тем больше емкостное сопротивление.[4]
Поэтому чем быстрее меняется направление тока, тем меньше емкостное сопротивление.
- Индуктивным сопротивлением XC обладают катушки индуктивности, создающие магнитное поле, которое препятствует изменению направления тока в цепи.[3]
-

4
Вычислите индуктивное сопротивление. Это сопротивление прямо пропорционально быстроте изменения направления тока, то есть частоты тока. Эта частота обозначается символом ƒ и измеряется в герцах (Гц). Формула для расчета индуктивного сопротивления: XL = 2πƒL, где L — индуктивность, измеряемая в генри (Гн).[5]
- Индуктивность L зависит от количества витков в катушке индуктивности.[6]
Также вы можете измерить индуктивность. - Если вы знакомы с единичной окружностью, то представьте, что один цикл переменного тока равен одному полному вращению этой окружности (на 2π радиан). Если умножить это значение на ƒ, которая измеряется в герцах (единиц в секунду), вы получите результат, измеряемый в радианах в секунду. Это единица измерения угловой скорости, которая обозначается через ω. Вы можете переписать формулу для вычисления индуктивного сопротивления так: XL=ωL[7]
- Индуктивность L зависит от количества витков в катушке индуктивности.[6]
-

5
Вычислите емкостное сопротивление. Это сопротивление обратно пропорционально быстроте изменения направления тока, то есть частоты тока. Формула для вычисления емкостного сопротивления: XC = 1 / 2πƒC.[8]
С — это емкость конденсатора, измеряемая в фарадах (Ф).- Вы можете измерить электрическую емкость.
- Эту формулу можно переписать так: XC = 1 / ωL (объяснения см. выше).
Реклама
-

1
Если цепь состоит исключительно из резисторов, то импеданс вычисляется следующим образом. Сначала измерьте сопротивление каждого резистора или посмотрите значения сопротивления на схеме цепи.[9]
- Если резисторы соединены последовательно, то полное сопротивление R = R1 + R2 + R3…
- Если резисторы соединены параллельно, то полное сопротивление R = 1 / R1 + 1 / R2 + 1 / R3 …
-

2
Сложите одинаковые реактивные сопротивления. Если в цепи присутствуют исключительно катушки индуктивности или исключительно конденсаторы, то полное сопротивление равно сумме реактивных сопротивлений. Вычислите его следующим образом:[10]
- Последовательное соединение катушек: Xtotal = XL1 + XL2 + …
- Последовательное соединение конденсаторов: Ctotal = XC1 + XC2 + …
- Параллельное соединение катушек: Xtotal = 1 / (1/XL1 + 1/XL2 …)
- Параллельное соединение конденсаторов: Ctotal = 1 / (1/XC1 + 1/XC2 …)
-

3
Вычтите индуктивные и емкостные сопротивления, чтобы получить общее реактивное сопротивление. Так как при возрастании одного типа сопротивления другое уменьшается, то они, как правило, компенсируют друг друга. Чтобы найти общее реактивное сопротивление, вычтите меньшее сопротивление из большего.[11]
- Или воспользуйтесь формулой: Xtotal = |XC – XL|
-

4
Вычислите импеданс по активному и реактивному сопротивлениям в последовательной цепи. Нельзя просто сложить эти величины, так как они меняются с течением времени, но достигают максимальных значений в разное время.[12]
Поэтому воспользуйтесь формулой:Z = √(R2 + X2).[13]
- Вычисления по этой формуле включают в себя использование векторов, но вы можете воспользоваться теоремой Пифагора, представив R и X в качестве катетов прямоугольного треугольника, а сопротивление Z — как гипотенузу.[14]
[15]
- Вычисления по этой формуле включают в себя использование векторов, но вы можете воспользоваться теоремой Пифагора, представив R и X в качестве катетов прямоугольного треугольника, а сопротивление Z — как гипотенузу.[14]
-

5
Вычислите импеданс по активному и реактивному сопротивлениям в параллельной цепи. В этом случае используются комплексные числа (это единственный способ вычислить полное сопротивление в параллельной цепи, в которой есть как активное, так и реактивное сопротивление).
- Z = R + jX, где j — мнимая единица: √(-1). Используйте j вместо i, чтобы не перепутать мнимую единицу (j) с силой тока (I).
- Складывать эти числа нельзя. Например, полное сопротивление может быть представлено так: 60 Ом + j120 Ом.
- Если у вас есть две последовательные цепи, то вы можете отдельно сложить натуральные числа и отдельно — комплексные. Например, если Z1 = 60 Ом + j120 Ом, а к этой цепи последовательно подключен резистор с Z2 = 20Ω, то Ztotal = 80Ω + j120Ω.
Реклама
Советы
- Общее сопротивление (активное и реактивное сопротивления) также может быть выражено через мнимое число.
Реклама
Об этой статье
Эту страницу просматривали 168 436 раз.