Как найти температуру при которой плотность газа

Температура газа при заданной плотности газа Калькулятор

Search
Дом	Химия ↺
Химия	Концепция родинки и стехиометрия ↺
Концепция родинки и стехиометрия	Плотность газов ↺

Температура газа при заданной плотности газа Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Давление газа: 0.215 паскаль –> 0.215 паскаль Конверсия не требуется
Молярная масса: 44.01 Грамм на моль –> 0.04401 Килограмм на моль (Проверьте преобразование здесь)
Плотность газа в г/л: 4.65 Грамм на литр –> 4.65 Килограмм на кубический метр (Проверьте преобразование здесь)

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

0.000244738723498394 Кельвин –> Конверсия не требуется

17 Плотность газов Калькуляторы

Температура газа при заданной плотности газа формула

Температура газа = (Давление газа*Молярная масса)/([R]*Плотность газа в г/л)

T_g = (P_gas*M_molar)/([R]*ρ_g/l)

Что такое уравнение идеального газа?

Идеальный газ определяется как гипотетическое газообразное вещество, поведение которого не зависит от сил притяжения и отталкивания и может быть полностью описано законом идеального газа. PV = nRT Это уравнение известно как закон идеального газа.

Молекулы всех газов при одной и той же
температуре обладают одинаковой средней
кинетической энергией. Причем давление
газа при данной температуре зависит
только от числа молекул в единице объема
газа. В основе объяснений физических
свойств газов и законов газового
состояния лежит кинетическая теория.
Большинство законов газового состояния
было выведено для идеального газа.
Идеальным называют газ, в котором
молекулы рассматриваются как материальные
точки, обладающие массой, но не имеющие
при этом объёма, между которыми отсутствуют
силы взаимодействия.

При
больших объёмах и малых давлениях, когда
расстояние между молекулами во много
раз больше собственных размеров молекул,
а также при высоких температурах, когда
интенсивность хаотического движения
молекул велика и поэтому молекулы слабо
взаимодействуют между собой, складываются
условия, при которых реальный газ можно
с некоторым приближением считать
идеальным.

Закон Бойля — Мариотта.
Английский ученый
Бойль и независимо от него несколько
позднее французский физик Мариотт на
основании экспериментов пришли к выводу
о том, что объем данной
массы газа и его давление находятся в
обратно пропорциональной зависимости.

Эта зависимость между давлением и
объемом газа при постоянной температуре
выражается формулой:

, (1)

где V₁
и Р₁
– объем и абсолютное давление газа до
их изменения; V₂
и Р₂ –
то же, после изменения.

Из данной формулы можно получить
следующие математические выражения:

, (2)

или

при

. (3)

Из последней формулы следует,
что произведение
давления данной массы газа на его объем
постоянно, если температура газа не
меняется.

Закон
имеет практическое применение в газовом
хозяйстве. Он позволяет определять
объем газа при изменении его давленная
и давление газа при изменении его объема
при условии, что температура газа
остаётся постоянной.

Чем больше при постоянной
температуре увеличивается объем газа,
тем меньше становится его плотность.
Зависимость между
объёмом газа и его плотностью при
постоянной температуре выражается
формулой

, (4)

где V₁
и V₂
– объемы, занимаемые газом; ρ₁
и ρ₂
– плотности газа, соответствующие этим
объемам.

Если в формуле (1) заменим отношение
объемов газа отношением их плотностей,
то на основании формулы (4) можно получить.

или

(5)

Из формулы (5) можно сделать
вывод, что при одной
и той же температуре плотности газов
прямо пропорциональны давлениям, под
которым находятся эти газы, т.е. плотность
газа (при постоянной температуре) будет
тем больше, чем больше будет его давление.

Пример.
Объем газа при давлении 760 мм.рт.ст. и
при температуре 0°С составляет 300 м³.
Какой объем займет этот газ при абсолютном
давлении, равном 1520 мм.рт.ст. и при той
же температуре?

760 мм.рт.ст. = 101 320 Па = 101,3 кПа;

1520 мм.рт.ст. = 202 630 Па = 202,6 кПа.

Подставляем заданные
значения V₁,
Р₁,
и Р₂
в формулу (2):

Р₁ =
101,3 кПа; V₁
= 300 м³;
Р₂ =
202,6 кПа;

101,3 х 300 = 202,6 V₂,
откуда V₂
= (101,3
х 300)/202,6 = 150 м³.

Закон Гей-Люссака.
Французский химик Гей-Люссак впервые
установил зависимость объема газа от
температуры при постоянном давлении.
Сущность этой зависимости заключается
в том, что при постоянном
давлении относительное изменение объема
данной массы газа прямо пропорционально
изменению температуры.
Математически эта зависимость между
объемом и температурой газа при постоянном
давлении записывается следующим образом:

, (6)

где V
– объем газа, м³;
Т – абсолютная
температура, К.

Из формулы (6) следует, что
если определенный
объем газа нагревать при постоянном
давлении, то его объем изменится во
столько раз, во сколько раз изменится
его абсолютная температура.

Многочисленные опыты
показывают, что при нагревании газов
на 1 градус при постоянном давлении их
объем увеличивается на постоянную
величину, равную 1/273,2 первоначального
их объема. Эта величина называется
термическим
коэффициентом объемного расширения
и обозначается α
= 1/273,2 град^-1.

С учетом этого закон
Гей-Люссака можно сформулировать так:
объем данной массы
газа при постоянном давлении увеличивается
линейно при повышении температуры

; (7)

; (8)

, (9)

где V_t
и V₀
– объемы газа при
конечной и начальной температурах, м³;
t
и Т – начальная и конечная температуры,
^оС,
К; α – термический коэффициент объёмного
расширения.

Из формулы (9) следует, что
объем газа при постоянном
давлении прямо пропорционален его
абсолютной температуре.

Закон Шарля.
Согласно закону Шарля,
давление данной массы
газа при постоянном объеме прямо
пропорционально абсолютной температуре.
Из этого закона следует, что отношение
давлений массы газа при постоянном
объеме равно отношению его абсолютных
температур. Закон
выражается следующей формулой:

или

, (10)

где Р₁
и Р₂
– абсолютные давления; Т₁
и
Т₂
– абсолютные температуры
газа, К.

Из формулы (10) можно сделать вывод, что
при постоянном объеме давление газа
при нагревании увеличивается во столько
раз, во сколько раз увеличивается его
абсолютная температура.

Пример 1.
При температуре газа 27°С его давление
равно 4 МПа (40 кгс/см²).
Каково будет избыточное давление этого
газа при температуре 47°С?

Начальная абсолютная
температура газа равна:

,

конечная абсолютная
температура газа равна:

.

Атмосферное давление примем
равным 0,1 МПа (1 кгс/см²),
тогда абсолютное давление газа до
нагревания будет:

.

Искомое абсолютное давление
газа Р₂
по формуле (10) равное:

.

Следовательно, избыточное давление
газа после нагревания его до 47°С равно:

.

Пример 2.
Сжатый газ в баллоне при температуре
7°С имел избыточное давление 0,9МПа. После
нагревания давление в баллоне повысилось
до 1,1 МПа. До какой температуры был нагрет
газ?

Начальная абсолютная
температура газа:

.

Начальное абсолютное
давление газа:

.

Конечное абсолютное давление
газа:

.

Из формулы (10) после
преобразования ее относительно
неизвестной Т₂
получаем:

.

Следовательно, газ в баллоне был нагрет
до температуры 63°С.

Закон
Авогадро. Итальянский
ученый Амадео Авогадро выразил
предположение, что различные
газы, занимающие одинаковые объёмы при
равных условиях (одинаковые давление
и температура), содержат одинаковое
число молекул.

Это число для одной
грамм-молекулы (1 моль) любого газа
составляет около N
= 6,064 ^х
10²³
и называется числом Авогадро. В дальнейшем
было экспериментально установлено, что
1 грамм-молекула любого газа при нормальных
условиях занимает объем 22,4л.

В Международной системе
единиц производной является величина,
в 1000 раз большая моля, она называется
киломоль и
обозначается кмоль.
1 кмоль любого газа
при нормальных условиях (0°С и 101,3 кПа)
занимает объем 22,4 м³.
Зная эту величину, можно определить
плотность любого газа по формуле

, (11)

где М —
масса 1 кмоля газа, кг.

Пример 1.
Определить плотность метана при
нормальных условиях (О^оС
и 101,3 кПа):

.

Пример 2. В баллоне находится 100 кг
жидкого этана. Определить объем паров
этана, полученных при его полном испарении
в нормальных условиях.

Решение. Сначала определяют число
киломолей этана:

п = 100 : 30,07 = 3,33 (здесь 30,07 –
молекулярная масса этана).

Зная, что 1 киломоль этана при испарении,
т.е. в газообразном состоянии, занимает
объем 22,4 м³, находят объем паров
этана от испарения всего его количества:

V = 22,4 ^х
3,33 = 74,63 м³.

Уравнение Клапейрона —
Менделеева.
При одновременном изменении объема,
давления и температуры газа справедливы
законы и Бойля — Мариотта и Гей-Люссака.

Французский ученый Клапейрон пришел к
выводу о существовании для газов
некоторой универсальной функции. Русский
ученый Д.И. Менделеев вывел в более общем
виде уравнение состояния идеальных
газов, объединив уравнения законов
Бойля — Мариотта и Гей-Люссака в одно
общее математическое уравнение идеального
газа, которое называется уравнением
Клайперона—Менделеева:

. (12)

Величина

обозначается буквой “R”
называется газовой постоянной. Подставляя
обозначение газовой постоянной в формулу
(12), получаем выражение:

или

. (13)

Это
уравнение закона газового состояния
связывает все три основных параметра
данного количества газа: объем, абсолютное
давление и абсолютную температуру, и
оно относится к 1 молю газа.

Из уравнения следует, что
для определенного
количества газа произведение его объема
на абсолютное давление равно произведению
газовой постоянной на абсолютную
температуру газа. Числовое
значение газовой постоянной зависит
от величин параметров, входящих в
уравнение (13).

В Международной системе универсальная
газовая постоянная для 1 кмоля равна:

,

где 101325 – нормальное давление, Па.

Уравнением Клапейрона —
Менделеева часто пользуются при пересчете
характеристик газа. Формулы (14) и (15),
предназначенные для пересчета параметров,
характеризующих состояние газа в
нормальных и стандартных условиях,
получены путем соответствующих,
преобразований выражения

.

, (14)

, (15)

где V_Н V_ст
– объём газа при нормальных и стандартных
условиях, м³; V_t
– объём газа при реальных условиях, м³;
P_t –
давление газа при реальных условиях,
Па; Р – давление газа при нормальных и
стандартных условиях (101325 Па).

Закон Дальтона.
Смеси газов (паров),
близких по своим свойствам к идеальным,
характеризуются аддитивностью парциальных
давлений. Аддитивность
(от лат. additivus
– прибавляемый), свойство объекта, по
которому величина всего объекта равна
сумме величин частей объекта при любом
разбиении. Так, масса тела равна сумме
масс его частей.

Парциальным давлением
компонента ρ_i
газовой смеси называется то давление,
которое этот компонент оказывал бы,
если бы из смеси удалить все другие
компоненты при сохранении первоначальных
объема и температуры системы. Закон
аддитивности записывается следующим
образом:

(16)

где π — общее давление смеси
газов (паров). Из уравнения

следует, что

(17)

Подставив это выражение в уравнение
(17), получим

(18)

Следовательно

(19)

или

(20)

т.е. парциальное
давление компонента равно давлению
системы, умноженному на мольную долю
этого компонента в газовой фазе.

Пример. Известен молярный состав
смеси газов, %: метан – 90, этан – 5, пропан
– 2, азот – 2, бутаны – 1. Смесь находится
под давлением 12 МПа. Требуется определить
парциальное давление компонентов смеси.

Решение. Пользуясь уравнением, вычисляют
парциальное давление компонентов:

p_C1
= 0,9*12 = 10,8 МПа;

p_C2
= 0,05*12 = 0,6 МПа;

p_C3
= 0,02*12 = 0,24 МПа;

p_C4
= 0,02*12 = 0,24 МПа;

p_C5
= 0,01*12 = 0,12 МПа.

Законы реальных газов.
При повышении давления
объем реального газа становится меньше,
чем идеального. Это
обстоятельство учитывают введением
соответствующих поправок в законы
идеальных газов.

Так,
уравнение состояния реального газа
можно записать в виде:

(21)

где z
— коэффициент сжимаемости, являющийся
функцией приведенного давления Р_пр
= P/P_кр
и приведенной
температуры T_пр
= T/Т_кр;
Р_кр
и Т_кр
— критические давление и температура
(табличные значения).

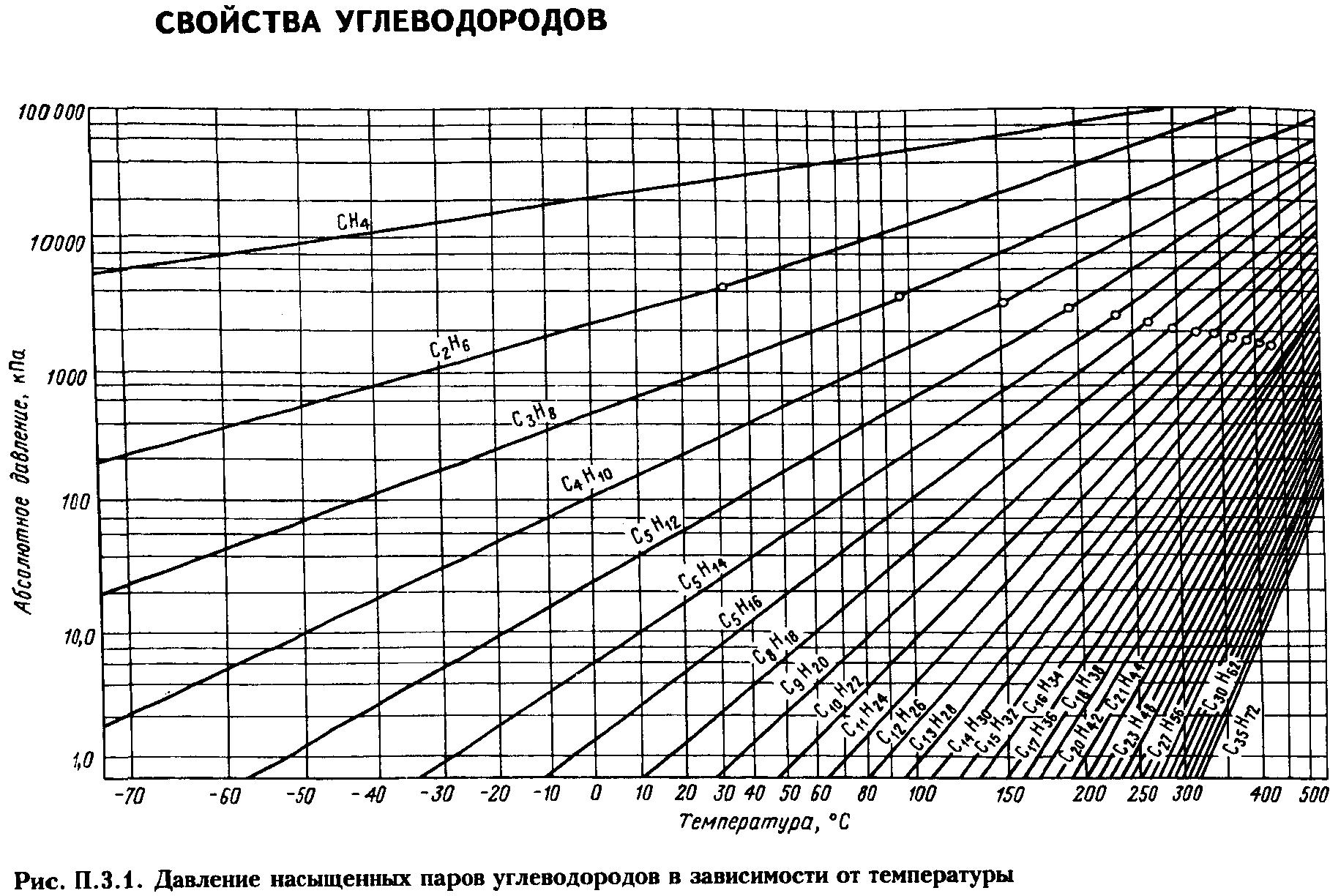
Давление насыщенных
паров. Пары жидкости
могут быть насыщенными и ненасыщенными.
Насыщенным называется
пар, находящийся в равновесии с жидкостью.
Чем выше температура, тем выше давление,
при котором находится данная равновесная
система. Для насыщенных паров существует
однозначная зависимость между давлением
паров и температурой Р
= f(T).

Ненасыщенными (перегретыми)
парами называют пары, которые при данных
температуре и давлении образуют
однофазную систему.
Жидкая фаза отсутствует.

Известно, что жидкость
начинает кипеть при такой температуре,
при которой давление её насыщенных
паров Р
становится равным внешнему давлению
π. Давление насыщенных паров определяют
по табличным данным или эмпирическим
уравнениям (ур-е Антуана, Киреева).

Для определения ДНП
нефтепродуктов, представляющих собой
сложные смеси углеводородов различных
классов, предложены графики и формулы
(Кокса, Ашворта, Вильсона, BWR
и др.)

Закон Рауля. Этот закон
устанавливает зависимость между
парциальным давлением компонента,
входящего в состав раствора, его молярной
концентрацией в жидкой смеси Х
и упругостью пара того же чистого
компонента при заданной температуре
Q.

Парциальное давление компонента в
жидкой смеси равно его молярной
концентрации, умноженной на упругость
его паров в чистом виде при данной
температуре:

(22)

где р – парциальное давление
компонента в растворе.

По закону Рауля, сумма парциальных
давлений всех компонентов равна общему
давлению над смесью или общей упругости
паров смеси:

где
Х_nQ_n
– молярная концентрация и упругость
паров компонента соответственно.

Пример. Жидкая смесь состоит из
этана –60%, пропа­на –25 % и изобутана
–15 % (молярные доли). Требуется оп­ределить
общее давление системы при температуре
10⁰С.

Решение. Сначала из рис. 2.1 (график Кокса)
находим давление насыщенных паров
компонентов в чистом виде при 10°С:

Q_C2
= 0,326 МПа; Q_C3
= 0,63 МПа; Q_C4
= 0,16 МПа

Затем по уравнению определим общее
давление системы:

Данные этого примера показывают, что
если бы указанная смесь транспортировалась
в жидком виде при 10°С, то трубопровод
работал под давлением 2,14 МПа.

Важным выводом, вытекающим из закона
Рауля, является то, что высококипящие
компоненты имеют низкую упругость,
содержатся в паровой фазе в малых
количествах; следователь­но, их
основная доля находится в жидкой фазе.
Что касается низкокипящих компонентов,
обладающих высокой упругостью, то они
легко переходят в газовую фазу. На этом
положении основана работа многих
установок по частичной стабилизации
газового конденсата при выветривании
– ступенчатом снижении давления смеси
с одновременным ее расширением.

23

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Макеты страниц

как посчитать плотность природного газа при заданной температуре

КК

Ученик

(127),
закрыт

14 лет назад