Как найти точки в которых функция положительна

Рассмотрим задания из №6 ЕГЭ, в которых по графику функции требуется определить точки, в которых производная положительна либо отрицательна.

№1

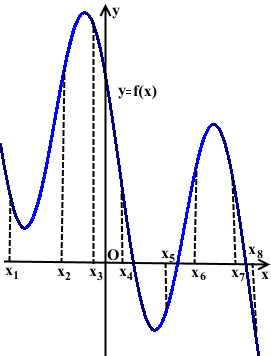
На рисунке изображён график дифференцируемой функции y=f(x). На оси абсцисс отмечены восемь точек: x₁, x₂ ,x₃, x₄, … , x₈. Среди этих точек найдите все точки, в которых производная функции f(x) положительна. В ответе укажите количество найденных точек.

Решение:

Производная функции f'(x) положительна там, где функция y=f(x) возрастает:

f'(x)>0, если f(x) возрастает.

Выделяем промежутки возрастания функции y=f(x) и определяем количество точек, принадлежащих этим промежуткам.

Промежуткам возрастания функции y=f(x) принадлежат три точки:  x₂, x₅ и x₆.

Значит, производная функции в этих трёх точках положительна:

f'(x₂)>0,

f'(x₅)>0,

f'(x₆)>0.

Ответ: 3.

№2

На рисунке изображён график функции y=f(x) и отмечены девять точек на оси абсцисс: x₁, x₂ ,x₃, x₄ …x₈, x₉. В скольких из этих точек производная функции f(x) отрицательна?

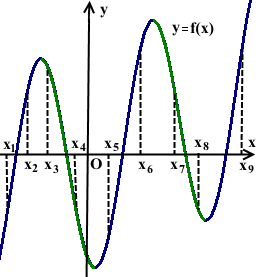
Решение:

Производная функции f'(x) отрицательна там, где функция y=f(x) убывает:

f'(x)<0, если f(x) убывает.

Выделяем промежутки убывания функции y=f(x) и определяем количество точек, принадлежащих этим промежуткам.

Промежуткам убывания функции y=f(x) принадлежат четыре точки:  x₃, x₄, x₇ и x₈. Значит, производная в этих четырёх точках отрицательна:

f'(x₃)<0, f'(x₄)<0, f'(x₇)<0, f'(x₈)<0.

Ответ: 4.

№3

На рисунке изображен график функции y=f(x), определенной на интервале (−6; 12). Определите количество целых точек, в которых производная функции положительна.

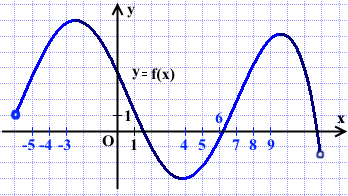
Решение:

Производная функции f'(x) положительна там, где функция y=f(x) возрастает.

Выделяем промежутки возрастания.

Целые точки, входящие в промежутки возрастания: -5; -4; -3; 4; 5; 6; 7; 8; 9.

Всего девять точек.

Ответ: 9.

Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).

Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.

Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.

Ответ: (11.)

Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.

На этой странице вы узнаете

• Где проходит граница между теплом и холодом? 
• Почему успех фильма не всегда зависит от наличия экшн-сцен?
• Чем кофе похож на функцию, ее первообразную и производную?  

Многие из нас чем-то похожи на родителей. Не являясь их точной копией, мы перенимаем определенные черты. То же самое происходит и с графиками. О том, какие особенности “наследуют” друг у друга графики функции, производной и первообразной, поговорим в статье. 

Связь графика функции и производной

Подготовим карандаши и линейки, мы начинаем погружение в мир графиков. Почему графики — это круто? Они дают нам наглядное представление о функции. Мы можем проанализировать ее, не прибегая к сложным формулам и трудоемким вычислениям. 

Воспринимать визуальную информацию всегда легче. А графики — это как раз визуальное описание функции. 

Возьмем график произвольной функции. 

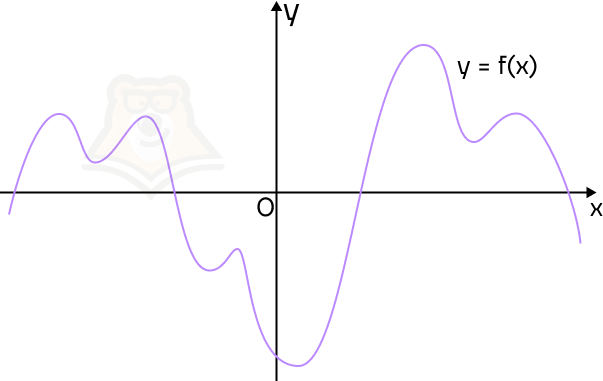
Прежде чем приступать к дальнейшему изучению материала, рекомендуем ознакомиться с «Определением и графиком функции», а также «Производной».

Мы точно видим, на каких промежутках график будет возрастать, а на каких убывать. Если представить, что мы пойдем по направлению оси х, то график будет возрастать на подъемах в горку и убывать на спусках с нее. Отметим промежутки возрастания зеленым фоном, а промежутки убывания красным. 

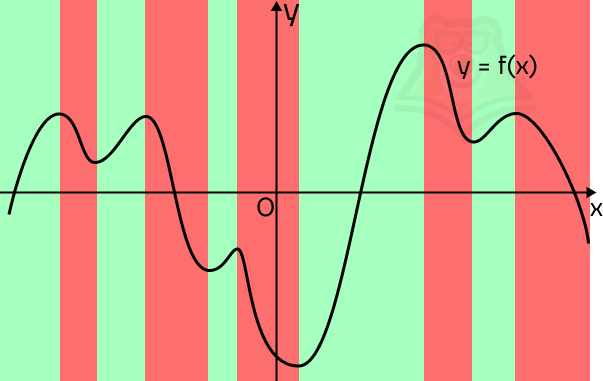
В зеленых промежутках производная будет положительна, а в красных отрицательна. Пока что просто запомним этот факт. 

Обратим внимание на границы между зелеными и красными зонами. В этих точках функция будет менять свой знак с положительного на отрицательный или обратно. Такие точки называются точками экстремума. 

Экстремум — это точка, в которой достигается максимальное или минимальное значение функции на заданном отрезке. 

Точки экстремума — точки, в которых достигается экстремум. 

В точках экстремума производная равна 0.

Теперь попробуем построить примерный график производной. Для начала опустим точки экстремума. Где они будут лежать на графике производной? На оси х. 

Вспомним, что в точках экстремума производная функции будет равна 0. Пусть график будет задан 

y = f'(x), тогда в точках экстремума получаем y = 0. Это и есть ось х. 

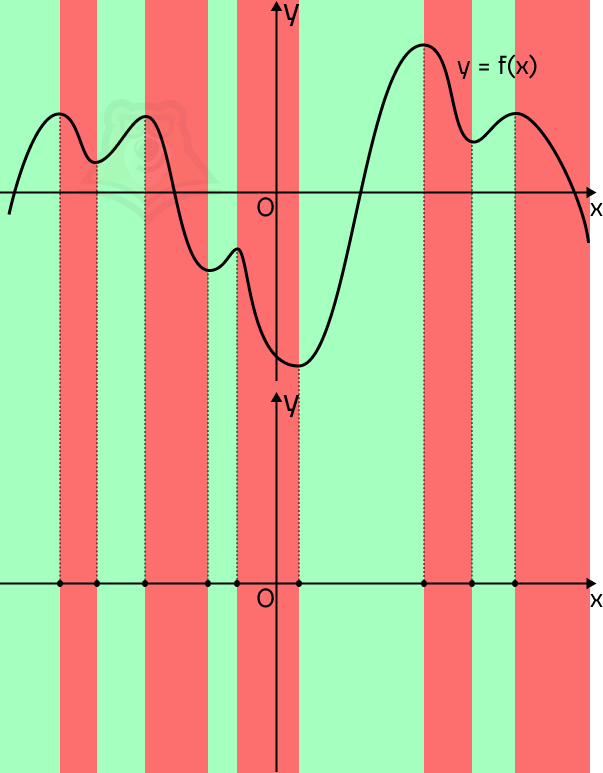
Так мы получили целых 9 точек, через которые пройдет производная. Осталось провести через них примерный график. 

Вспомним, что:

• производная положительна на промежутках возрастания функции;
• производная отрицательна на промежутках убывания функции. 

Как понять, что все точки на графике производной будут положительны или отрицательны? Достаточно посмотреть на то, с какой стороны от оси х они располагаются. 

Положительные значения всегда будут лежать выше оси х. Это связано со значением y: значения функции будут положительны при положительных значениях у, и отрицательны при отрицательных значениях у. 

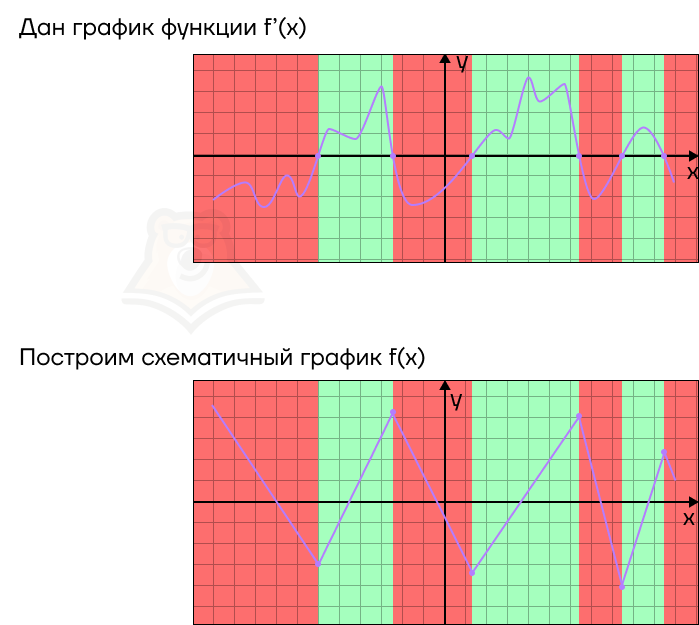
Итак, как нам нарисовать график производной? На зеленых участках ее график будет лежать над осью х, а на красных участках — под ней. 

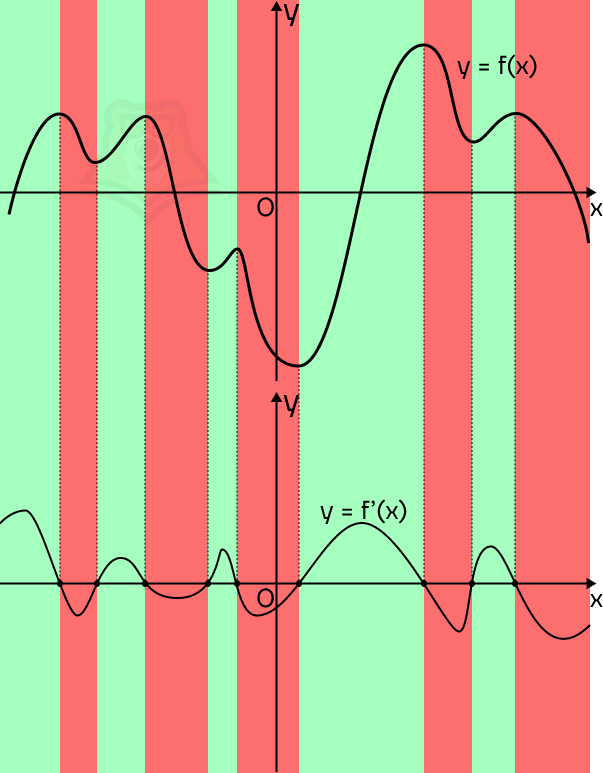
Подведем итоги:

• В точках экстремума функции график производной будет проходить через ось х.
• На промежутках возрастания функции график производной будет лежать выше оси х.
• На промежутках убывания функции график производной будет лежать ниже оси х. 

Эти зависимости можно отследить на любых графиках функции и ее производной. 

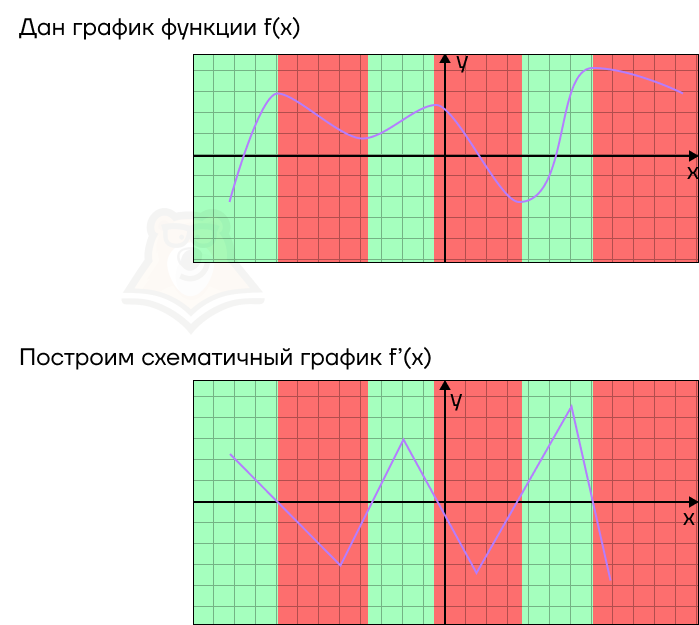
Если провести обратные рассуждения, то по графику производной можно восстановить примерный график функции. В этом случае:

• В точках, где график производной пересекает ось х, будут лежать точки экстремума. При этом если в точке производная меняет значение с положительного на отрицательное, то это точка максимума, а если с отрицательного на положительное, то это точка минимума. 
• На промежутках, где график производной будет лежать выше оси х, функция будет возрастать. 
• На промежутках, где график производной будет лежать ниже оси х, функция будет убывать. 

Разберем несколько примеров, где можно применить эти знания. 

Пример 1. На рисунке изображен график функции f(x) и отмечены пять точек на оси абсцисс: x₁, x₂, x₃, x₄, x₅. В скольких из этих точек производная функции отрицательна?

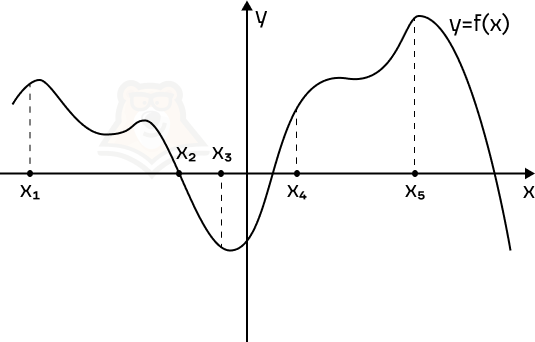
Решение. Производная отрицательна на промежутках убывания функции. Отметим такие промежутки. 

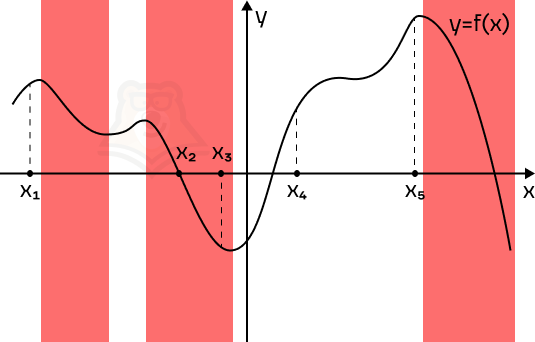
В точках, которые попали в эти промежутки, производная отрицательная. Всего таких точек 2.

Ответ: 2

Пример 2. На рисунке изображен график функции y = f'(x) — производной функции f(x), определенной на интервале (-5; 3). Найдите точку максимума функции f(x).

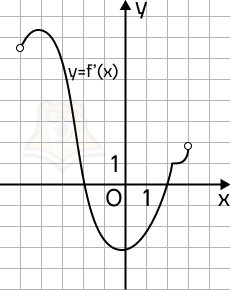
Решение. Точки экстремума на графике производной лежат на оси х. На данном графике таких точки две: x = -2, x = 2. 

Точка максимума — это точка, в которой производная меняет знак с положительного на отрицательный. По графику определяем, что это точка x = -2.

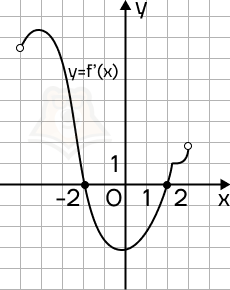
Ответ: -2

Связь графика функции и первообразной

Мы разобрались, как связаны графики функции и ее производной. Есть ли связь между графиком функции и «Первообразной»?

Вспомним один важный факт: если взять производную от первообразной, то получим функцию. 

F'(x) = f(x)

Похоже на функцию и ее производную, верно? На самом деле, ситуации ничем не отличаются. 

В этом случае изначальной функцией будет первообразная, а ее производной — функция. Для наглядности составим таблицу. 

	Было	Взяли производную	Стало
Функция и производная	f(x)	f'(x)	f'(x)
Функция и первообразная	F(x)	F'(x)	f(x)

Получается, для функции и первообразной будут действовать почти те же правила, что и для функции и ее производной. 

При решении заданий с графиками первообразной достаточно проанализировать уравнение F'(x) = f(x). Рассмотрим несколько примеров. 

Пример 3. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x) и отмечены шесть точек на оси абсцисс x₁, x₂, x₃, x₄, x₅, x₆. В скольких из этих точек функция f(x) отрицательна? 

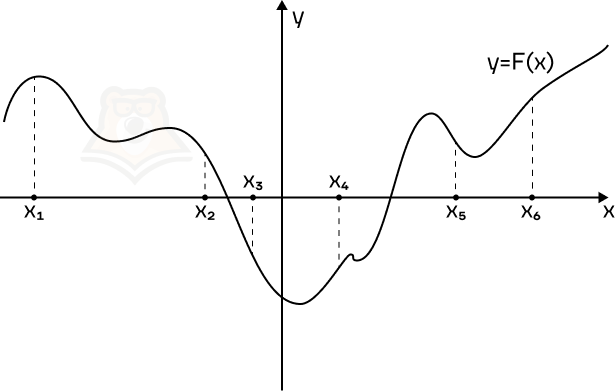
Решение. Поскольку F'(x) = f(x), то функция f(x) будет отрицательна в тех же точках, в которых будет отрицательна F'(x). 

Поскольку на графике изображена функция y = F(x), то ее производная будет отрицательна на промежутках убывания функции. Отметим их красным. 

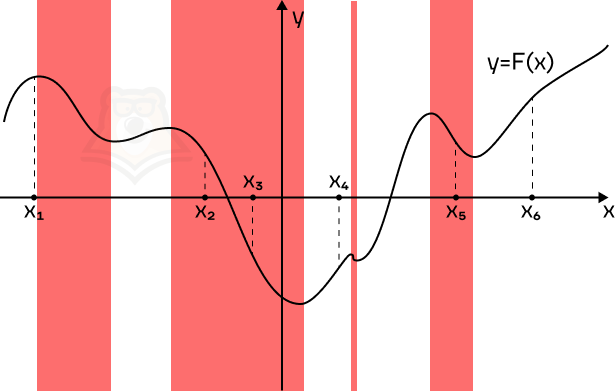
В эти промежутки попадают 3 из 6 точек.  

Ответ: 3. 

Пример 4. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x), определенной на интервале (-6; 7). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-5; 4]. 

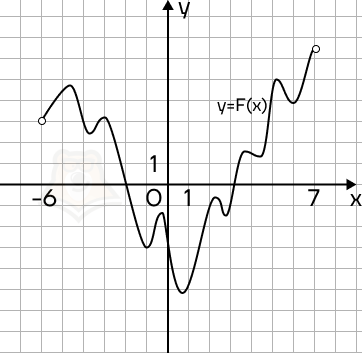
Решение. Вспомним, что F'(x) = f(x). Тогда если f(x) = 0, то и F'(x) = 0. Следовательно, на заданном промежутке нужно найти точки экстремума. 

Отметим заданный промежуток красными линиями. На промежутке всего 9 точек экстремума, значит, в 9 точках f(x) будет равна 0. 

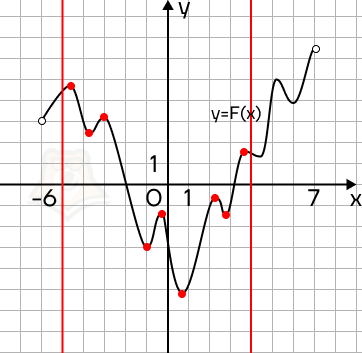
Ответ: 9

Фактчек

• Графики функции, производной и первообразной связаны между собой. 
• В точках экстремума функции график производной будет проходить через ось х.
• На промежутках возрастания функции график производной будет лежать выше оси х.
• На промежутках убывания функции график производной будет лежать ниже оси х. 
• Для решения задач с первообразной необходимо вспомнить, что F'(x) = f(x). Любой график можно проанализировать с помощью этого уравнения также, как анализируются графики функции и ее производной. 

Проверь себя

Задание 1. 
На каких промежутках будет производная функции будет положительна?

1. На промежутках убывания функции.
2. На промежутках возрастания функции.
3. В точках экстремума.
4. Невозможно определить по графику. 

Задание 2. 
На каких промежутках производная функции будет отрицательна?

1. На промежутках возрастания функции.
2. На промежутках убывания функции.
3. В точках экстремума.
4. Невозможно определить по графику. 

Задание 3. 
На рисунке изображен график производной функции f(x), на котором отмечена точка. Чем будет являться эта точка для функции f(x)? 

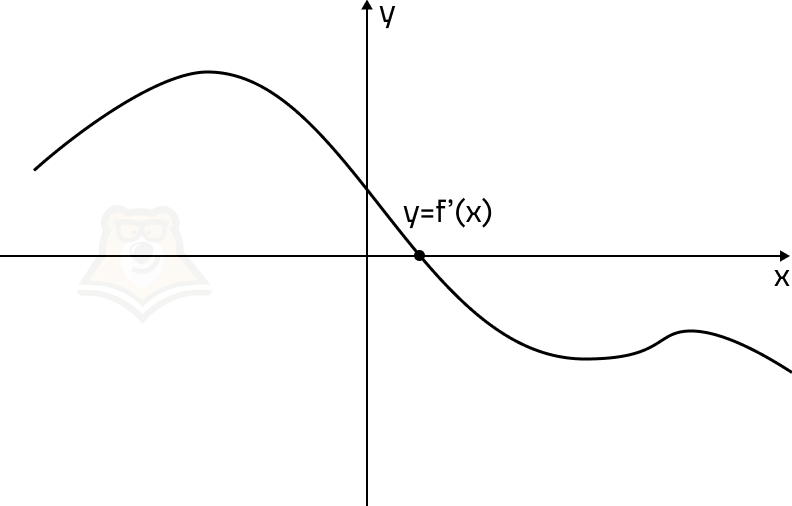
1. Точка максимума функции.
2. Точка минимума функции.
3. Любая произвольная точка на функции.
4. Невозможно определить по графику. 

Задание 4. 
Выберите верный вариант:

1. F(x) = f'(x)
2. F(x) = f(x)
3. F'(x) = f'(x)
4. F'(x) = f(x)

Ответы: 1. — 2 2. — 2 3. — 1 4. — 4

Исследование функции с помощью производной. В этой статье мы с вами разберём некоторые задачи связанные с исследованием графика функции. В таких задачах, даётся график функции y = f (x) и ставятся вопросы, связанные с определением количества точек, в которых производная функции положительна (либо отрицательна), а также  другие. Их относят к заданиям на применение производной к исследованию функций.

Решение таких задач, и вообще задач связанных с исследованием, возможно только при полном понимании свойств производной для исследования графиков функций и геометрического смысла производной. Поэтому настоятельно рекомендую вам изучить соответствующую теорию. Можете изучить статью на блоге, а также посмотреть справочник (но в нём краткое изложение).

Задачи, где дан график производной мы будем также рассматривать в будущих статьях, не пропустите! Итак, задачи:

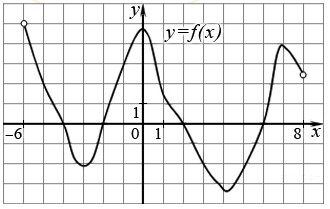
На рисунке изображен график функции у = f (х), определенной на интервале (−6; 8). Определите:

1. Количество целых точек, в которых производная функции отрицательна;

2. Количество точек, в которых касательная к графику функции параллельна прямой у = 2;

3. Количество точек, в которых производная равна нулю;

1. Производная функции отрицательна на интервалах, на которых функция убывает, то есть на интервалах (−6; –3), (0; 4,2), (6,9; 8). В них содержатся целые точки  −5,  −4,  1, 2, 3, 4,  и  7. Получили  7 точек.

2. Прямая  y = 2 параллельная оси ох.  Касательная будет параллельна прямой  y = 2 только в точках  экстремума (в точках, где график меняет своё поведение  с возрастания на убывание или наоборот). Таких точек четыре:  –3; 0; 4,2; 6,9

3. Производная равна нулю в четырёх точках (в точках экстремума), их мы уже указали.

Решите самостоятельно:

Определите количество целых точек, в которых производная функции положительна.

Посмотреть решение.

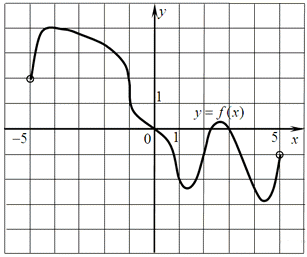
На рисунке изображен график функции у = f (х), определенной на интервале (−5; 5). Определите:

1. Количество целых точек, в которых производная функции положительна;

2. Количество целых точек, в которых касательная к графику функции параллельна прямой у = 3;

3. Количество точек, в которых производная равна нулю;

1. Из свойств производной функции известно, что она положительна на  интервалах, на которых функция возрастает, т. е. на интервалах (1,4; 2,5) и (4,4;5). В них содержится только  одна целая точка х = 2.

2. Прямая  y = 3 параллельная оси ох.  Касательная будет параллельна прямой  y = 3 только в точках  экстремума (в точках, где график меняет своё поведение  с возрастания на убывание или наоборот).

Таких точек четыре:  –4,3; 1,4; 2,5; 4,4

3. Производная равна нулю в четырёх точках (в точках экстремума), их мы уже указали.

Решите самостоятельно:

Определите количество целых точек, в которых производная функции  f (x) отрицательна.

Посмотреть решение.

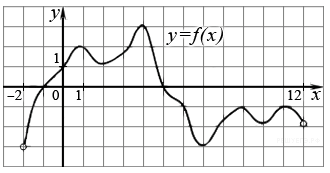
На рисунке изображен график функции у = f (х), определенной на интервале  (−2; 12). Найдите:

1. Количество целых точек, в которых производная функции положительна;

2. Количество целых точек, в которых производная функции отрицательна;

3. Количество целых точек, в которых касательная к графику функции параллельна прямой у = 2;

4. Количество точек, в которых производная равна нулю.

1. Из свойств производной функции известно, что она положительна на  интервалах, на которых функция возрастает, т. е. на интервалах (–2; 1), (2;4), (7; 9) и (10;11). В них содержатся целые точки:   –1, 0, 3, 8. Всего их четыре.

2. Производная функции отрицательна на интервалах, на которых функция убывает, то есть на интервалах (1; 2), (4; 7), (9; 10), (11;12). В них содержатся целые точки  5  и  6. Получили  2 точки.

3. Прямая  y = 2 параллельная оси ох.  Касательная будет параллельна прямой  y = 2 только в точках  экстремума (в точках, где график меняет своё поведение  с возрастания на убывание или наоборот). Таких точек семь:  1; 2; 4; 7; 9; 10; 11.

4. Производная равна нулю в семи точках (в точках экстремума), их мы уже указали.

Решите самостоятельно:

Найдите сумму точек экстремумов функции f (x). Посмотреть решение.

Как видите, ничего сложного нет. Желаю вам успехов!

С уважением, Александр Крутицких

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Печать страницы