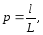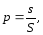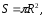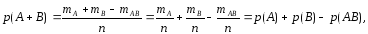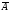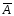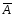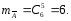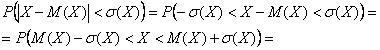Как найти вероятность попадания точки на отрезок - Сайт, где вы сможете решить свои вопросы

Лекция 2.

Геометрические
вероятности. Теорема сложения вероятностей.
Противоположные события. Условные
вероятности. Теорема умножения
вероятностей. Независимые события.
Вероятность появления хотя бы одного
события.

Одним из недостатков
классического определения вероятности
является то, что оно неприменимо к
испытаниям с бесконечным количеством
исходов. В таких случаях можно
воспользоваться понятием геометрической
вероятности.

Пусть на отрезок
L
наудачу брошена точка. Это означает,
что точка обязательно попадет на отрезок
L
и с равной возможностью может совпасть
с любой точкой этого отрезка. При этом
вероятность попадания точки на любую
часть отрезка L
не зависит
от расположения этой части на отрезке
и пропорциональна его длине. Тогда
вероятность того, что брошенная точка
попадет на отрезок l,
являющийся частью отрезка L,
вычисляется по формуле:

(2.1)

где l
– длина
отрезка l,
а L
– длина
отрезка L.

Можно дать
аналогичную постановку задачи для
точки, брошенной на плоскую область S
и вероятности того, что она попадет на
часть этой области s:

(2.1`)

где s
– площадь
части области, а
S
– площадь
всей области.

В трехмерном случае
вероятность того, что точка, случайным
образом расположенная в теле V,
попадет в его часть
v,
задается формулой:

(2.1“)

где v
– объем
части тела, а
V
– объем
всего тела.

Пример 1. Найти
вероятность того, что точка, наудачу
брошенная в круг, не попадет в правильный
шестиугольник, вписанный в него.

Решение. Пусть
радиус круга равен R
, тогда сторона шестиугольника тоже
равна R.
При этом площадь круга

а площадь шестиугольника
Следовательно,

Пример 2. На отрезок
АВ
случайным образом брошены три точки:
С,
D
и М.
Найти вероятность того, что из отрезков
АС, АD
и АМ
можно построить треугольник.

Решение. Обозначим
длины отрезков АС,
АD
и АМ
через x,
y
и
z
и рассмотрим в качестве возможных
исходов множество точек трехмерного
пространства с координатами (х,
у, z).
Если принять длину отрезка равной 1, то
эти множество возможных исходов
представляет собой куб с ребром, равным
1. Тогда множество благоприятных исходов
состоит из точек, для координат которых
выполнены неравенства треугольника: x
+ y
> z,
x
+ z
> y,
y
+ z
> x.
Это часть
куба, отрезанная от него плоскостями x
+ y
= z,
x
+ z
= y,
y
+ z
= x

х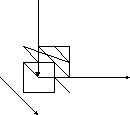Рис.1.

(одна из них,
плоскость x
+ y
= z,
проведена
на рис.1). Каждая такая плоскость отделяет
от куба пирамиду, объем которой равен
.
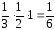
Следовательно, объем оставшейся части

.
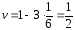
Тогда

Теорема
сложения вероятностей.

Теорема 2.1
(теорема сложения).
Вероятность
р(А
+ В) суммы
событий А
и В
равна

Р(А+В)=р(А)+р(В)–р(АВ).
(2.2)

Доказательство.

Докажем теорему
сложения для схемы случаев. Пусть п
– число возможных исходов опыта, т_А
– число исходов, благоприятных событию
А,
т_В
– число
исходов, благопри-ятных событию В,
а т_АВ
– число
исходов опыта, при которых происходят
оба события (то есть исходов, благоприятных
произведению АВ).
Тогда число исходов, при которых имеет
место событие А
+ В, равно т_А
+ т_В
– т_АВ
(так как в
сумме (т_А
+ т_В)
т_АВ
учтено
дважды: как исходы, благоприятные А,
и исходы, благоприятные В).
Следовательно, вероятность суммы можно
определить по формуле (1.1):

что и требовалось
доказать.

Следствие 1.
Теорему 2.1
можно распространить на случай суммы
любого числа событий. Например, для
суммы трех событий А,
В и
С

Р(А+В+С)=р(А)+р(В)+р(С)–р(АВ)–р(АС)–р(ВС)+р(АВС)
(2.3)

и т.д.

Следствие 2. Если
события А и
В несовместны,
то т_АВ
= 0, и, следовательно, вероятность суммы
несовместных событий равна сумме их
вероятностей:

Р(А+В)=р(А)р(В).
(2.4)

Определение 2.1.
Противоположными
событиями
называют два несовместных события,
образующих полную группу. Если одно из
них назвать А,
то второе принято обозначать
.

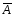
Замечание.
Таким образом,

заключается в том, что событие А
не произошло.

Теорема 2.2.
Сумма
вероятностей противоположных событий
равна 1:

р(А)+р(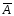)=1.
(2.5)

Доказательство.

Так как А
и

образуют полную группу, то одно из них
обязательно произойдет в результате
опыта, то есть событие А
+
является достоверным. Следовательно,

Р(А+)=1.
Но, так как А
и
несовместны, из (2.4) следует, что
Р(А+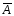)=р(А)+р().
Значит, р(А)+р(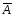)=1,
что и требовалось доказать.

Замечание. В
ряде задач проще искать не вероятность
заданного события, а вероятность события,
противоположного ему, а затем найти
требуемую вероятность по формуле (2.5).

Пример. Из урны,
содержащей 2 белых и 6 черных шаров,
случайным образом извлекаются 5 шаров.
Найти вероятность того, что вынуты шары
разных цветов.

Решение. Событие
,
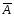
противоположное заданному, заключается
в том, что из урны вынуто 5 шаров одного
цвета, а так как белых шаров в ней всего
два, то этот цвет может быть только
черным. Множество возможных исходов
опыта найдем по формуле (1.5):

а множество исходов,
благоприятных событию

– это число возможных наборов по 5 шаров
только из шести черных:

Тогда

а

Теорема
умножения вероятностей.

Определение 2.2.
Назовем
условной
вероятностью р(В/А)
события В
вероятность
события В
при условии, что событие А
произошло.

Замечание. Понятие
условной вероятности используется в
основном в случаях, когда осуществление
события А
изменяет вероятность события В.

Примеры:

пусть событие А
– извлечение из колоды в 32 карты туза,
а событие В
– то, что и вторая вынутая из колоды
карта окажется тузом. Тогда, если после
первого раза карта была возвращена в
колоду, то вероятность вынуть вторично
туз не меняется:

Если же первая карта в колоду не
возвращается, то осуществление события
А
приводит к тому, что в колоде осталась
31 карта, из которых только 3 туза. Поэтому
если событие А
– попадание в самолет противника при
первом выстреле из орудия, а В
– при втором, то первое попадание
уменьшает маневренность самолета,
поэтому р(В/А)
увеличится по сравнению с р(А).

Теорема 2.3
(теорема умножения). Вероятность
произведения двух событий равна
произведению вероятности одного из них
на условную вероятность другого при
условии, что первое событие произошло:

р(АВ)=р(А)·р(В/А).
(2.6)

Доказательство.

Воспользуемся
обозначениями теоремы 2.1. Тогда для
вычисления р(В/А)
множеством возможных исходов нужно
считать т_А
(так как А
произошло), а множеством благоприятных
исходов – те, при которых произошли и
А,
и В
( т_АВ
). Следовательно,

откуда следует
утверждение теоремы.

Пример. Для поражения
цели необходимо попасть в нее дважды.
Вероятность первого попадания равна
0,2, затем она не меняется при промахах,
но после первого попадания увеличивается
вдвое. Найти вероятность того, что цель
будет поражена первыми двумя выстрелами.

Решение. Пусть
событие А
– попадание при первом выстреле, а
событие В
– попадание при втором. Тогда р
(А)
= 0,2, р
(В/А)
= 0,4, р
(АВ)
= 0,2·0,4 = 0,08.

Следствие.
Если подобным образом вычислить
вероятность события ВА,
совпадающего с событием АВ,
то получим, что р(ВА)=р(В)·р(А/В).
Следовательно,

р(А)·р(В/А)=р(В)·р(А/В).
(2.7)

Определение 2.3.
Событие В
называется независимым
от события
А,
если появление события А
не изменяет вероятности В,
то есть р
(В/А)
= р
(В).

Замечание. Если
событие В
не зависит от А,
то и А
не зависит от В.
Действительно, из (2.7) следует при этом,
что р (А)
· р (В)
= р (В)
· р (А/В),
откуда р
(А/В)
= р (А).
Значит, свойство
независимости событий взаимно.

Теорема умножения
для независимых событий имеет вид:

р (АВ)=р(А)·р(В),
(2.8)

то есть вероятность
произведения независимых событий равна
произведению их вероятностей.

При решении задач
теоремы сложения и умножения обычно
применяются вместе.

Пример. Два стрелка
делают по одному выстрелу по мишени.
Вероятности их попадания при одном
выстреле равны соответственно 0,6 и 0,7.
Найти вероятности следующих событий:

А
– хотя бы одно попадание при двух
выстрелах;

В –
ровно одно попадание при двух выстрелах;

С
– два попадания;

D
– ни одного попадания.

Решение. Пусть
событие Н₁
– попадание первого стрелка, Н₂
– попадание второго. Тогда

А=Н₁+Н₂,
В=Н₁
События Н₁
и Н₂
совместны и независимы, поэтому теорема
сложения применяется в общем виде, а
теорема умножения – в виде (2.8).
Следовательно, р(С)=0,6·0,7
= 0,42, р(А)
= 0,6 + 0,7 – 0,42 = 0,88,

р(B)
= 0,6·0,3 + 0,7·0,4 = 0,46 (так как события

и

несовместны),

р(D)
= 0,4·0,3
= 0,12. Заметим, что события А
и D
являются противоположными, поэтому

р(А)
= 1 – р(D).

Вероятность
появления хотя бы одного события.

Теорема 2.4.
Вероятность появления хотя бы одного
из попарно независимых событий

А₁,
А₂,…,
А_п
равна

р (А)
= 1 – q₁q₂…q_n
, (2.9)

где q_i
– вероятность
события
,
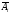
противоположного событию А_i
.

Доказательство.

Если событие А
заключается в появлении хотя бы одного
события из А₁,
А₂,…,
А_п,
то события А
и

противоположны, поэтому по теореме 2.2
сумма их вероятностей равна 1. Кроме
того, поскольку А₁,
А₂,…,
А_п независимы,
то независимы и
,
следовательно, р()=.
Отсюда следует справедливость формулы
(2.9).

Пример. Сколько
нужно произвести бросков монеты, чтобы
с вероятностью не менее 0,9 выпал хотя
бы один герб?

Решение. Вероятность
выпадения герба при одном броске равна
вероятности противопо-ложного события
(выпадения цифры) и равна 0,5. Тогда
вероятность выпадения хотя бы одного
герба при п
выстрелах равна 1- (0,5)^п
. Тогда из
решения неравенства 1- (0,5)^п
> 0,9

следует, что п
>
log₂10
≥ 4.

Соседние файлы в папке Лекции 2 курс

Источник

Геометрическая вероятность

Геометрическая вероятность на прямой
Геометрическая вероятность на плоскости
Геометрическая вероятность в пространстве
Примеры

Понятие геометрической вероятности было сформулировано в §37 данного справочника. В этом параграфе мы рассмотрим различные задачи, при решении которых используется геометрическая вероятность.

п.1. Геометрическая вероятность на прямой

В одномерном случае пространству всех событий соответствует длина отрезка Ω ↔ L. Событие A ↔ l_A – попадание в отрезок l_A ≤ L.
Тогда вероятность события A $$ mathrm{ P(A)=frac{l_A}{L} } $$ Говорят, что мерой множеств событий в одномерном случае является длина.

Например:
Оптический кабель длиной 1 м случайно разрезают ножницами. Какова вероятность того, что длина обрезка составляет не меньше 80 см?

Чтобы получить обрезок не менее 80 см, нужно попасть ножницами в отрезок 20 см справа или слева куска кабеля. Вероятности попадания (mathrm{P_{text{справа}}=frac{l_A}{L}, P_{text{слева}}=frac{l_A}{L}}). По правилу суммы, искомая вероятность при L=100 см, l_A=20 см $$ mathrm{ P_{text{справа}}+P_{text{слева}}=frac{2l_A}{L}, P=frac{2cdot 20}{100}=0,4 } $$ Ответ: 0,4.

п.2. Геометрическая вероятность на плоскости

В двумерном случае пространству всех событий соответствует площадь некоторой замкнутой области Ω ↔ S_Ω.
Событие A ↔ s_A – попадание в замкнутую подобласть с площадью s_A ≤ S_Ω.
Тогда вероятность события A $$ mathrm{ P(A)=frac{s_A}{S_{Omega}} } $$ Говорят, что мерой множеств событий в двумерном случае является площадь.

Например:
Два друга договорились встретиться между 14 и 15 часами. Каждый может прийти в любой момент в течение назначенного часа. Тот, кто пришёл первым, ждёт другого в течение 15 минут, а затем уходит. Чему равна вероятность встречи?

Пусть 0≤x≤60 (мин) и 0≤y≤60 (мин) – моменты прихода первого и второго друга соответственно. Тогда пространство событий – квадрат 60х60.
Область ожидания: |x–y|≤15. Раскроем модуль: –15≤x–y≤15. Получаем систему: (left{ begin{array}{ l} mathrm{yleq x+15} &\ mathrm{ygeq x-15} & end{array}right. ). На графике – это зелёная полоса. Событие A – встреча состоялась – соответствует площади зеленой полосы. Получаем: begin{gather*} mathrm{ S_{Omega}=60cdot 60=3600, s_A=3600-2S_{Delta}=3600-2cdot frac{1}{2}cdot 45^2=1575 }\ mathrm{ P(A)=frac{s_A}{S_{Omega}}=frac{1575}{3600}=frac{7}{16}=0,4375 } end{gather*} Ответ: 0,4375.

п.3. Геометрическая вероятность в пространстве

В трёхмерном случае пространству всех событий соответствует объём некоторой замкнутой области Ω ↔ V_Ω.
Событие A ↔ v_A – попадание в замкнутую подобласть с объёмом v_A ≤ V_Ω.
Тогда вероятность события A $$ mathrm{ P(A)=frac{v_A}{V_{Omega}} } $$ Говорят, что мерой множеств событий в трёхмерном случае является объём.

Например:
Телескоп находится на космической станции. В каждый момент времени он случайно направлен в одну из сторон и наблюдает часть неба. Пусть телескоп способен регистрировать все объекты в радиусе 10000 км. Какова вероятность, что он заметит астероид радиусом 100 км, залетевший в область регистрации?

Пространству всех событий соответствует сфера объемом: $$ mathrm{ V_{Omega}=frac{4}{3}pi R^3, R=10000 text{км} } $$ Событие A – астероид замечен – соответствует объему астероида: $$ mathrm{ v_{A}=frac{4}{3}pi R^3, R=100 text{км} } $$ Вероятность того, что астероид будет замечен: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}}=frac{frac{4}{3}pi R^3}{frac{4}{3}pi R^3}=left(frac{r}{R}right)^3, P(A)=left(frac{100}{10000}right)^3=10^{-6}=0,000001 } $$ Ответ: 0,000001.

п.4. Примеры

Пример 1. Для игры в «Дартс» используется круглая мишень радиусом 40 см. Центральный круг – «десятка» – имеет радиус 4 см. Если игрок всегда попадает в мишень в любую точку с одинаковой вероятностью, какова вероятность попасть в «десятку»?

Мерой для этой задачи является площадь.
Пространство всех событий – круг радиусом R = 40 см. Его площадь (mathrm{ S_{Omega;}=pi R^2}).
Событие A – попадание в «десятку» – круг радиусом r = 4 см. Его площадь (mathrm{ s_{A}=pi r^2}).
Вероятность попадания: $$ mathrm{ P(A)=frac{s_{A}}{S_{Omega}}=frac{pi r^2}{pi R^2}=left(frac{r}{R}right)^2, P(A)=left(frac{4}{40}right)^2=0,01 } $$ Ответ: 0,01.

Пример 2. В правильный треугольник вписан полукруг. В треугольник случайно ставятся точки. Какова вероятность, что точка попадет в полукруг?

Мерой в данной задаче является площадь.
Пусть сторона треугольника a. Тогда пространство всех событий – треугольник площадью (mathrm{ S_{Omega}=frac{sqrt{3}}{4}a^2}).
Найдем радиус вписанного полукруга.
ΔCOB ~ ΔOEB – по двум углам. $$ mathrm{ frac{CO}{OE}=frac{CB}{OB}Rightarrowfrac{acdot sin60^{circ}}{r}=frac{a}{a/2}Rightarrow r=frac{a}{2}cdot sin60^{circ}=frac{sqrt{3}}{4}a } $$ Площадь вписанного полукруга: (mathrm{ s_{A}=frac{pi r^2}{2}=frac{pi}{2}left(frac{sqrt{3}}{4}aright)^2=frac{3pi}{32}a^2}).
Вероятность попасть в полукруг: $$ mathrm{ P(A)=frac{s_{A}}{S_{Omega}}=frac{frac{3pi}{32}a^2}{frac{sqrt{3}}{4}a^2}=frac{sqrt{3}}{8}pi approx 0,68 } $$ Ответ: (mathrm{ frac{sqrt{3}}{8}pi approx 0,68. })

Пример 3. На отрезке [0; 1] случайным образом выбирается точка. Найдите вероятность того, что её координата x удовлетворяет условиям:
1) x² > 0,64
2) (left{ begin{array}{ l} mathrm{0,3x^2leq 0,027} &\ mathrm{2x^2geq 0,08} & end{array}right. )

1) (mathrm{x^2geq 0,64Rightarrow (x^2-0,64)geq 0Rightarrow (x-0,8)(x+0,8)geq 0Rightarrow} left{ begin{array}{ l} mathrm{xleq -0,8} &\ mathrm{xgeq 0,8} & end{array}right. )
Учитывая x ∈ [0; 1], получаем: $$ left{ begin{array}{ l} mathrm{0leq xleq 1} &\ left[ begin{array}{ l} mathrm{xleq -0,8Rightarrow 0,8leq xleq 1} &\ mathrm{xgeq 0,8} & end{array}right.& end{array}right. $$ Мерой в данной задаче является длина: L_Ω = 1, l_A = 1 – 0,8 = 0,2
Вероятность выбора точки при данных условиях: ( mathrm{P(A)=frac{0,2}{1}=0,2} )
begin{gather*} 2) left{ begin{array}{ l} mathrm{0,3x^2leq 0,027} &\ mathrm{2x^2geq 0,08} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{x^2leq 0,009} &\ mathrm{x^2geq 0,004} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{x^2-0,009leq 0} &\ mathrm{x^2-0,004geq 0} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{(x-0,3)(x+0,3)leq 0} &\ mathrm{(x-0,2)(x+0,2)geq 0} & end{array}right. Rightarrow \ Rightarrow left{ begin{array}{ l} mathrm{-0,3leq xleq 0,3} &\ left[ begin{array}{ l} mathrm{xleq -0,2} &\ mathrm{xgeq 0,2} & end{array}right.& end{array}right. Rightarrow left[ begin{array}{ l} mathrm{-0,3leq xleq -0,2} &\ mathrm{0,2leq xleq 0,3} & end{array}right. end{gather*} Учитывая x ∈ [0; 1], получаем: $$ left{ begin{array}{ l} mathrm{0leq xleq 1} &\ left[ begin{array}{ l} mathrm{-0,3leq xleq -0,2} &\ mathrm{0,2leq xleq 0,3} & end{array}right.& end{array}right. Rightarrow 0,2 leq x leq 0,3 $$ Мерой в данной задаче является длина: L_Ω = 1, l_A = 0,3 – 0,2 = 0,1
Вероятность выбора точки при данных условиях: (mathrm{P(A)=frac{0,1}{1}=0,1})
Ответ: 1) 0,2; 2) 0,1.

Пример 4. В сито, наполненное до краёв зерном, уронили жемчужину. Сито представляет собой цилиндр радиусом 20 см и высотой 12 см.
1) Какова вероятность случайно зачерпнуть горсть зерна вместе с жемчужиной, если объём горсти 0,1 л?
2) Если после неудачной попытки, высыпать зерно из горсти обратно в сито, перемешать, и снова зачерпнуть горсть, изменится ли вероятность?
3) Если после неудачной попытки, высыпать зерно из горсти в сторону и зачерпнуть следующую горсть, изменится ли вероятность?
4) Сколько «неудачных» горстей нужно отсыпать в сторону, чтобы вероятность удачи для следующей попытки превысила 1/3?
1) Мерой для этой задачи является объём.
Пространство всех событий – все возможные точки, где может оказаться жемчужина – это цилиндрическое сито, объемом

V_Ω = πR²h, R = 20 см = 2 дм, h = 12 см = 1,2 дм
V_Ω = π · 2² · 1,2 = 4,8 π дм³ = 4,8 π л

Событие A – зачерпнуть жемчужину в горсти объемом v_A = 0,1 л
Вероятность: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}}, P(A)=frac{0,1}{4,8pi} approx 0,0066 } $$ 2) Если высыпать зерно обратно из горсти и перемешать, то пространство всех событий останется тем же, V_Ω = 4,8π л. Вероятность не изменится.

3) Если высыпать зерно в сторону, пространство всех событий уменьшится:

V‘_Ω = V_Ω – v_A = (4,8π – 0,1) л

Вероятность увеличится: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}^{‘}}, P(A)=frac{0,1}{4,8pi -0,1} approx 0,0071 } $$
4) После того, как мы отсыпаем N горстей, пространство всех событий $$ mathrm{ V_{Omega}^{”} = V_{Omega}-Nv_{A}=(4,8pi-0,1N) text{л} } $$ По условию: $$ mathrm{ P(A)frac{0,1}{4,8pi -0,1N}geq frac13 } $$ Получаем: (mathrm{4,8pi -0,1Nlt 0,3Rightarrow Ngt frac{4,8pi-0,3}{0,1}=147,8})
N = 148.
Ответ: 1) 0,0066; 2) нет; 3) увеличится, 0,0071; 4) 148.

Пример 5. Загадываются два действительных числа от 0 до 4.
1) Какова вероятность, что их сумма больше 3?
2) Какова вероятность, что их разность меньше 1?

По условию 0 ≤ x ≤ 4, 0 ≤ y ≤ 4
Мерой для этой задачи является площадь.
Пространство всех событий: квадрат 4х4, S_Ω = 4² = 16.

Ответ: (mathrm{ 1) frac{23}{32}; 2) frac{7}{16}. })

Источник

Алгебра и начала математического анализа, 11 класс

Урок №37. Геометрическая вероятность.

Перечень вопросов, рассматриваемых в теме:

Геометрическая вероятность
Задачи на геометрическую вероятность

Глоссарий по теме

Испытанием называется осуществление определенных действий.

Под событием понимают любой факт, который может произойти в результате испытания.

Любой результат испытания называется исходом.

Достоверным называют событие, которое в результате испытания обязательно произойдёт.

Невозможным называют событие, которое заведомо не произойдёт в результате испытания.

Геометрической вероятностью некоторого события называется отношение P(A) = g/G, где G – геометрическая мера, выражающая общее число всех равновозможных исходов данного испытания, а g – мера, выражающая количество благоприятствующих событию A исходов

Основная литература:

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250

Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики. – 4-е изд. – М.: Просвещение, 1995. – 288 с.: ил. – ISBN 5-09-0066565-9. сс.253-259.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

Вероятность наступления некоторого события A в испытании равна P(A) = g/G, где G – геометрическая мера, выражающая общее число всех равновозможных исходов данного испытания, а g – мера, выражающая количество благоприятствующих событию A исходов.

Пусть на плоскости задана некоторая область D, площадь которой равна S(D), и в ней содержится область d, площадь которой равна s(d). В области D наудачу ставится точка. Тогда вероятность события А – «точка попадает в область d» равна числу P(A) = s(d)/S(D).

Рисунок 1 – иллюстрация геометрической вероятностей

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Вероятность попадания точки на отрезок l равна P(A) = |l|/|L|.

Пусть пространственная фигура d составляет часть фигуры D. В фигуру D наудачу ставится точка. Вероятность попадания точки в фигуру d равна P(A) = V(d)/V(D).

Пример использования геометрического определения вероятности при решении задачи.

Два друга договорились встретиться в определенном месте между 12 и 13 часами. Пришедший первым ждет другого в течении 20 минут, после чего уходит. Чему равна вероятность встречи друзей, если приход каждого из них может произойти

наудачу в течении указанного часа и моменты прихода независимы?

Решение:

х – момент прихода первого друга

y – момент прихода второго друга

0≤х≤60, 0≤у≤60

⎮х-у⎮≤20.

Сделаем рисунок

Рисунок 2 – Иллюстрация к задаче

S=60²–2·1/2·40²=2000

P(A) = 2000/60² = 5/9.

Ответ: вероятность встречи 5/9.

Примеры и разбор решения заданий тренировочного модуля

Пример 1. Метровый шнур случайным образом разрезают ножницами. Найти вероятность того, что длина обрезка составит не менее 80 см.

Решение:

Общему числу исходов соответствует длина шнура 1 м. Чтобы длина обрезка составила не менее 0,8 м, можно отрезать не более 0,2 м. Такие отрезы можно выполнить с любой стороны шнура, их суммарная длина равна 0,2+0,2=0,4 м. По геометрическому определению:

P(A)=l/L=0,4/1=0,4

Ответ: 0,4

Пример 2. В шар брошена случайная точка.

2а) С какой вероятностью она попадёт в центр шара?

Решение:

Объём одной точки (центра шара) равен нулю, значит и искомая вероятность равна 0

Ответ: 0

2б) С какой вероятностью она попадёт на какой-нибудь диаметр шара?

Решение:

Любая точка шара всегда попадает на какой-нибудь диаметр. Поэтому вероятность равна единице.

Ответ: 1.

2в) С какой вероятностью она попадёт в одно, определённое, полушарие?

Решение:

При решении этой задачи используем отношение объемов фигур. Пусть весь объём шара равен V. Все точки шара – трёхмерная фигура Ω. Искомая вероятность равна отношению объёма полушария V(A) к объёму шара V:

Ответ: 0,5

Пример 3. В круг радиуса см вписан равнобедренный прямоугольный треугольник. В круг наудачу ставится точка. Найдите вероятность того, что она не попадёт в данный треугольник. При необходимости в расчетах используйте значение π с точностью до целых.

Решение:

Площадь круга равна

Гипотенуза прямоугольного треугольника, вписанного в круг, равна диаметру круга (прямой угол опирается на диаметр), то есть .

Поскольку треугольник равнобедренный, его катеты равны между собой, и по теореме Пифагора каждый катет равен . Площадь такого треугольника будет равна (можно найти площадь треугольника, не вычисляя длины катета: рассмотрим квадрат со стороной, равной гипотенузе нашего треугольника, площадь такого квадрата в четыре раза больше площади треугольника

Вероятность попадания точки в треугольник равна отношению площадей треугольника и круга:

Ответ: 1/3

Источник

Скачать материал

Сейчас обучается 393 человека из 62 регионов

Сейчас обучается 271 человек из 64 регионов

Описание презентации по отдельным слайдам:

1 слайд

Геометрические вероятности
Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Если предположить, что вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L, то вероятность попадания точки на отрезок l определяется равенством
P= Длина l / Длина L

Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Если предположить, что вероятность попадания брошенной точки на фигуру gпропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g, то вероятность попадания точки в фигуру g определяется равенством
Р= Площадь g/ Площадь G
2 слайд

R
a
p =
Площадь окружности
Площадь квадрата
p =
•R2
a2
•R2
2R2
= = = 0,64

2
Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга.
Внутри круга радиусом R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг квадрата:
3 слайд

Сумма всех трех отрезков равна L, поэтому каждый из отрезков должен быть меньше L/2.
На отрезке АО длины L числовой оси Ох наудачу поставлены две точки: В(х) и С(у). Найти вероятность того, что из трех получившихся отрезков можно построить треугольник.
Решение:
Для того чтобы из трех отрезков можно было построить треугольник, каждый из отрезков должен быть меньше суммы двух других.
Введем в рассмотрение прямоугольную систему координат хОу. Координаты любых двух точек В и С должны удовлетворять двойным неравенствам:
0 < х < L,
0 < у < L.
Этим неравенствам удовлетворяют координаты любой точки М(х ; у), принадлежащей квадрату ОLDL. Таким образом этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют все возможные значения координат точек В и С.
О
L
L
D
х
у
М(х ; у)
№1
4 слайд

1. Пусть точка С расположена правее точки В.
Как указано выше должны выполняться неравенства:
ОВ < L/2,
ВС < L/2,
СА < L/2.
у < L/2,
х – у< L/2,
L – х < L/2.
0
В(х)
С(у)
А
L
х
ОС < L/2,
ВС < L/2,
ВА < L/2.
2. Пусть точка С расположена левее точки В.
Тогда должны выполняться неравенства:
0
С(у)
В(х)
А
L
х
или
или
или
или
х < L/2,
у < х + L/2,
у > L/2.
х < L/2,
у – х < L/2,
L – у < L/2.
у < L/2,
у > х – L/2,
х > L/2.
5 слайд

Таким образом заштрихованные треугольники можно рассматривать как фигуру g, координаты точек которой благоприятствуют интересующему нас события ( из трех отрезков можно построить треугольник). Искомая вероятность:
О
L
L
D
х
у
х < L/2,
у < х + L/2,
у > L/2.
1.
х = L/2
у = L/2
у = х – L/2
у = х + L/2
Е
К
Н
F
М
Эти неравенства выполняются для координат точек треугольника EFH.
у < L/2,
у > х – L/2,
х > L/2.
Эти неравенства выполняются для координат точек треугольника KLM..
2.
Р = = =
Sg
SG
S EFH + S KHM
SOLDL
1
4
Ответ:1/4
6 слайд

В сигнализатор поступают сигналы то двух устройств, причем поступление каждого из сигналов равновозможно в любой момент промежутка времени длительностью Т. Моменты поступления сигналов независимы один от другого. Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше t (t < T). Найдите вероятность того, что сигнализатор срабатывает за время Т, если каждое из устройств пошлет по одному из сигналов.
Решение:
Введем в рассмотрение прямоугольную систему координат хОу. Точки квадрата ОТАТ удовлетворяют данным неравенствам. Этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют все возможные значения моментов поступления сигналов.
О
Т
Т
А
х
у
№2
Обозначим моменты поступления сигналов первого и второго устройств через х и у соответственно. В силу условия задачи:
0 < х < Т,
0 < у < Т.
7 слайд

Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше t, т.е., если у –х < t при у > х и х – у < t при х > у, или, что то же,
у < х + t при у > х,
у > х – t при у < х.
Как видно из рисунка, все точки, координаты которых удовлетворяют этим неравенствам принадлежат заштрихованному шестиугольнику. Таким образом, этот шестиугольник можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими срабатыванию сигнализатора моментами времени х и у.
Искомая вероятность:
Р = = =
Sg
SG
T(2Т –t)
Т2
Т2 -2( Т – t )2/2
Т2
8 слайд

№3
В круг радиуса R вписан правильный треугольник. Внутрь круга наугад брошены четыре точки. Найти вероятности следующих событий:
а) все четыре точки попадут внутрь треугольника;
б) одна точка попадет внутрь треугольника и по одной точке попадет на каждый «малый сегмент».
Решение:
а) Найдем вероятность попадания всех точек в треугольник.
Sкруга=
П R2
R=
a
3
3а
2
а
( )
Sтреугольника =
3а
2
3а
2
а
( )
3а
2
а
( )
а2 3
= =
4
3R2 3
4
Р = = =
Sтреугольника
Sкруга
4П R2
3R2 3
4П
3 3
Вероятность попадания четырех точек в треугольник равна:
4П
3 3
( )4
Вероятность попадания одной точки в треугольник равна:
9 слайд

б) Найдем вероятность, что одна точка попадет внутрь треугольника и по одной точке попадет на каждый «малый сегмент».
4П
3 3
Вероятность попадания одной точки в треугольник равна:
(Sкруга- Sтреугольника):3=
Sсегмента=
3R2 3
4
(П R2 – )/3=
3R2 3
12
4П R2 –
Вероятность попадания одной точки в сегмент равна:
Р = = =
Sодного сегмента
Sкруга
П R2
3R2 3
12
4П R2 –
3 3
12 П
4П –
Вероятность попадания по одной точке на каждый сегмент равна:
3 3
12 П
4П –
( )3
3 3
12 П
4П –
( )3
4П
3 3
n!
Искомая вероятность Р=

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 250 694 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

Рейтинг:
4 из 5

11.01.2021
6260
331

11.01.2021
1366
0

11.01.2021
984
1

11.01.2021
980
0

11.01.2021
1087
9

11.01.2021
1020
1

11.01.2021
1512
6

Вам будут интересны эти курсы:

Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»
Курс повышения квалификации «Правовое обеспечение деятельности коммерческой организации и индивидуальных предпринимателей»
Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
Курс повышения квалификации «Экономика и право: налоги и налогообложение»
Курс повышения квалификации «Экономика предприятия: оценка эффективности деятельности»
Курс повышения квалификации «Этика делового общения»
Курс профессиональной переподготовки «Организация маркетинга в туризме»
Курс повышения квалификации «Организация маркетинга в туризме»
Курс профессиональной переподготовки «Организация деятельности помощника-референта руководителя со знанием иностранных языков»
Курс профессиональной переподготовки «Корпоративная культура как фактор эффективности современной организации»
Курс повышения квалификации «Актуальные вопросы банковской деятельности»
Курс профессиональной переподготовки «Организация деятельности по водоотведению и очистке сточных вод»

Источник

2.2.8. Вероятность попадания в промежуток

Найдём – вероятность того,

что случайная величина примет

какое-нибудь значение из интервала .

В данном случае концы интервала (–1 и 5) находятся в области непрерывности функции распределения поэтому: .
И действительно, на данном интервале находятся значения , вероятности появления которых: .
Вычислим вероятность . Оба

конца этого промежутка не «попадают» в точки разрыва, поэтому:
– вероятность того, что

случайная величина примет

значение из данного промежутка. И в самом деле – на нём находится единственное значение , которое может появиться с вероятностью .

Та же самая история с –

единственное, тут левый конец промежутка равен «минус» бесконечности:
– самостоятельно

проанализируйте, какие значения , и с какими вероятностями располагаются на промежутке

Теперь более занятная ситуация, где нужно особо включать голову: если хотя бы один из концов промежутка «попадает» в точку

разрыва функции , то указанную

выше формулу можно использовать лишь в одном случае из четырёх, а именно для неравенства:

Примечание: если , то

левое неравенство становится строгим, но формула тоже применима.

Найдём . Как быть? – под

правило не подходит! Вспоминаем теоремы тервера. По теореме сложения вероятностей несовместных событий:

– вероятность того, что

случайная величина примет

значение из отрезка .
И действительно, этот отрезок включает в себя два значения , которые появляются с вероятностями .

Тут же рассмотрим три других неравенства:
, т.к. на интервале нет значений случайной величины.

Да-да, так и пишем.

– это «штатный» случай

(см. правило).

И для 2-го полуинтервала используем теорему сложения вероятностей несовместных событий:

Едем дальше:

– поскольку там нет

значений случайной величины.

Кстати, случай с нестрогим неравенством – есть «штатный» случай:
, который можно оформить и

так:
– ведь на функции

распределения «свет клином не сошёлся».
И, наконец, типовая вероятность – того, что значение случайной величины отклонится от своего математического ожидания не более чем на одно среднее квадратическое отклонение. И, как вы догадываетесь, эти характеристики нужно