Как найти время подъема до максимальной высоты - Сайт, где вы сможете решить свои вопросы

1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту

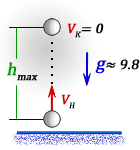
h_max
– максимальная высота достигнутая телом за время t

V_к – конечная скорость тела на пике, равная нулю

V_н – начальная скорость тела

t – время подъема тела на максимальную высоту h

g ≈ 9,8 м/с² – ускорение свободного падения

Формула максимальной высоты (h_max):

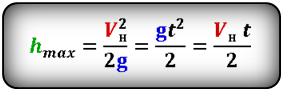
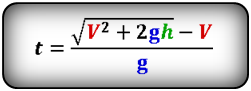
Формула времени за которое тело достигло максимальную высоту (t):

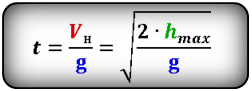
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести

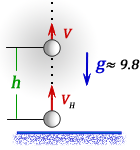
h – расстояние пройденное телом за время t

V_н – начальная скорость тела

V – скорость тела в момент времени t

t – время подъема за которое тело пролетело расстояние h

g ≈ 9,8 м/с² – ускорение свободного падения

Формула скорости тела в момент времени t (V):

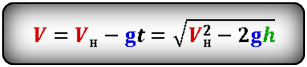
Формула начальной скорости тела (V_н):

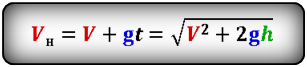
Формулы высоты тела в момент времени t (h):

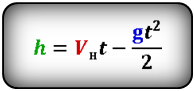
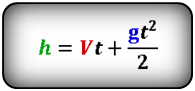
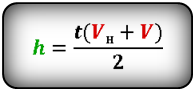
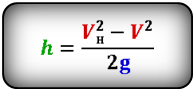
Формулы времени, за которое тело достигло высоту h (t):

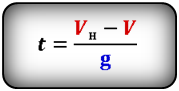
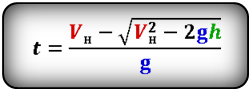
Подробности

Опубликовано: 04 августа 2015

Обновлено: 13 августа 2021

Источник

В статье подробно, начиная с основ и базовых определений, рассказано о движении тела брошенного под углом к горизонту. Здесь вы найдете формулы параметров движения: общее время, дальность полета, максимальная высота. Также в конце приложены примеры задач с решениями.

Определение. Баллистическое движение — это движение некоторого тела в поле тяжести Земли при условии, что тело имеет вертикальную и горизонтальную проекции скорости.

Вначале вспомним основные формулы для равноускоренного движения.

Изменение скорости с течением времени задаётся соотношением

vₓ = v₀ₓ + aₓt,

где vₓ — конечная проекция скорости, v₀ₓ — начальная проекция скорости, aₓ — проекция ускорения тела.

Изменение координаты x во времени можно найти, используя следующее соотношение:

x = x₀ + v₀ₓt + aₓt² / 2,

где x — конечная координата тела, x₀ — начальная координата, v₀ₓ — начальная проекция скорости тела вдоль оси OX, aₓ — проекция ускорения тела.

Рис. 1

Замечание 1. Перемещением тела за время t называется величина Sₓ = x – x₀.

Замечание 2. Так как эти выражения справедливы для проекций, то их можно записать и в векторном виде.

Баллистическое движение — это случай равноускоренного движения (с постоянным ускорением свободного падения g). Любое тело, брошенное под углом α к горизонту, имеет некоторую вертикальную и горизонтальную проекции скорости (рис. 1).

Далее движение необходимо разбить на два участка:

Горизонтальное
Вертикальное

По горизонтали тело движется с одинаковой скоростью (обычно пренебрегаем силами различного трения):

v₁ = v₀cos(α)

А по вертикали это обычное движение тела, брошенного вертикально вверх с начальной скоростью:

v₂ = v₀sin(α)

Общее время движения

Разобьём траекторию на два участка. Первый — участок, на котором тело продолжает подниматься, а второй — участок, где тело спускается. Обозначим t₁ время подъёма тела (от нуля до максимальной высоты подъема), t₂ — время спуска тела.

Из уравнения движения:

v₀sin(α) – gt₁ = 0

(так как конечная проекция скорости в верхней точке траектории равна нулю),

t₁ = v₀sin(α) / g.

Найдём время спуска:

–gt₂ = –v₀sin(α),

(т. к. конечная скорость тела будет такая же, как и начальная),

t₂ = v₀sin(α) / g.

Общее время движения:

t = t₁ + t₂ = 2v₀sin(α) / g.

Замечание.Время спуска и время подъёма тела одинаковые. Это связано с тем, что движение симметрично.

Дальность полета

Так как по горизонтали (вдоль оси ОХ) движение тела равномерное, то, зная общее время движения, найдём дальность полета L:

L = tv₁ = (2v₀sin(α) / g) · v₀cos(α) = 2v₀²sin(α)cos(α) / g.

Замечание. Используя формулу из тригонометрии

2sin(α)cos(α) = sin(2α),

получим:

L = 2v₀²sin(2α) / g.

Следовательно, максимальная дальность полета тела будет при броске под углом 45° к горизонту (так как sin(90°) = 1).

Максимальная высота подъёма тела

Рассмотрим движение тела в проекции на ось OY:

H = v₀sin(α)t₁ – gt₁² / 2.

После подставления времени подъёма получим

H = v₀²sin²(α) / (2g).

Давайте теперь решим некоторые задачи.

Задачи

Задача 1. Пуля, летящая горизонтально со скоростью v = 500 м/с, пробивает первый листок бумаги. Найти, на каком расстоянии S находится второй листок бумаги, если известно, что его пуля пробила на h = 20 см ниже, чем первый.

Решение. Найдём, за какое время пуля прошла расстояние между листами. Нам известно, что за это же время она опустилась на высоту h = 20 см. Тогда:

h = gt² / 2,

t = √(2h/g).

Теперь, зная время движения пули между листами, найдём расстояние, которое прошла пуля за это время:

S = tv = v · √(2h/g) = 100 м.

Ответ: S = 100 м.

Задача 2. Школьник может бросить мяч в спортивном зале с максимальной скоростью v = 25 м/с. Пренебрегая силами сопротивления воздуха, найти максимальную дальность полета мяча в спортивном зале, если высота зала равна h = 4 м. Считать, что мяч не ударяется о потолок.

Решение. Пусть мальчик бросил мяч под некоторым углом α к горизонту. Тогда дальность полета мяча равна:

L = 2v₀²sin(α)cos(α) / g.

Как обсуждалось выше, тело имеет максимальную дальность полета, если его бросить под углом α = 45° к горизонту. Но в данной задаче возможно, что при таком угле мяч ударится о потолок. Проверим, какова максимальная высота подъёма мяча при условии, что угол равен α = 45°.

H = v₀²sin²(α) / (2g) = 16 м.

Следовательно, угол, под которым мальчик бросит мяч, будет значительно меньше. Найдём максимальный угол, при котором мяч не столкнется с потолком. Этот угол будет соответствовать предельному случаю, когда мяч побывает на высоте h = 4 м.

h = v₀²sin²(α) / (2g) => sin²(α) = 2gh / v₀².

Из основного тригонометрического тождества

sin²(α) + cos²(α) = 1

найдём cos²(α):

cos²(α) = 1 – 2gh / v₀².

Подставив все выражения в дальность полета L, получим:

L = 2√(2gh(v₀² – 2gh)) / g = 42 м.

Ответ: L = 42 м.

Замечание. Если в задаче не приведены числовые значения (задача в общем виде), то необходимо записать 2 ответа. Первый ответ при условии высокого потолка, при h > H —

L = 2v₀²sin(α)cos(α) / g, α = 45°.

И при h < H получаем ответ

L = 2√(2gh(v₀² – 2gh)) / g.

Список литературы

Черноуцан А. Учебно-справочное пособие для старшеклассников и абитуриентов. М., 2000.
Белолипецкий С. Н., Еркович О. С., Казаковцева В. А., Цвецинская Т. С. Задачник по физике. М., 2005.

Автор: Роман Федоренко

Источник

Содержание

Как найти скорость подъема тела с поверхности земли брошенного вверх?
Шаг 1. Определите начальную скорость тела.
Шаг 2. Найдите время подъема тела.
Шаг 3. Определите высоту, на которую было брошено тело.
Шаг 4. Определите скорость тела на максимальной высоте.
Шаг 5. Найдите скорость тела на любой другой высоте.
В заключение
Как найти скорость подъема тела с поверхности земли брошенного вверх
Как работает формула подъема тела
Решение задачи на примере
Методы расчета скорости подъема
Итог
Как найти скорость подъема тела с поверхности земли брошенного вверх
Что такое скорость подъема тела?
Как вычислить скорость подъема тела?
Пример расчета скорости подъема тела
Вывод

Как найти скорость подъема тела с поверхности земли брошенного вверх?

Некоторые из нас могут помнить, что на уроках физики в школе они изучили, как найти скорость тела при его движении с постоянной скоростью или ускорении. Но что делать, если тело брошено вверх с начальной скоростью? Как определить скорость его подъема? В этой статье мы разберемся в этом вопросе.

Шаг 1. Определите начальную скорость тела.

Начальная скорость тела — это скорость, с которой оно было брошено вверх. Если у вас есть данные о высоте, на которую было брошено тело, и времени, за которое оно достигло максимальной высоты, вы можете использовать формулу:

v₀ = (h / 2) / t

Здесь v₀ — начальная скорость тела, h — высота, на которую было брошено тело, t — время подъема тела до максимальной высоты.

Шаг 2. Найдите время подъема тела.

Время подъема тела до максимальной высоты можно найти с помощью формулы:

t = √(2h / g)

Здесь t — время подъема тела до максимальной высоты, h — высота, на которую было брошено тело, g — ускорение свободного падения (≈9,81 м/с²).

Шаг 3. Определите высоту, на которую было брошено тело.

Если у вас есть данные о времени подъема тела и максимальной высоте, которую оно достигло, вы можете использовать формулу:

h = (1 / 2)gt²

Здесь h — высота, на которую было брошено тело, g — ускорение свободного падения (≈9,81 м/с²), t — время подъема тела до максимальной высоты.

Шаг 4. Определите скорость тела на максимальной высоте.

На максимальной высоте скорость тела равна нулю. Это происходит потому, что, достигнув максимальной высоты, тело останавливается на короткое время, прежде чем начать падать вниз, ускоряясь вследствие ускорения свободного падения.

Шаг 5. Найдите скорость тела на любой другой высоте.

Скорость тела в любой точке его движения можно найти с помощью формулы:

v = √(v₀² — 2gh)

Здесь v — скорость тела на любой высоте, v₀ — начальная скорость тела, g — ускорение свободного падения (≈9,81 м/с²), h — высота, на которой находится тело.

В заключение

Найденная скорость подъема тела с поверхности земли брошенного вверх может быть полезна в различных задачах, связанных с механикой и физикой. Важно помнить, что для вычисления скорости тела необходимо знание его начальной скорости, высоты броска и времени подъема.

скорость подъема тела
брошенного вверх
начальная скорость тела
высота, на которую было брошено тело
время подъема тела
максимальная высота тела
ускорение свободного падения

Как найти скорость подъема тела с поверхности земли брошенного вверх

Астрофизические и физические процессы окружающего мира не перестают удивлять людей. Одним из таких процессов является движение тела, брошенного вверх с поверхности Земли. Определение скорости подъема этого тела является необходимым при решении физических задач и может быть найдено при помощи различных физических формул. В этой статье мы рассмотрим методы расчета скорости подъема тела с поверхности земли брошенного вверх.

Как работает формула подъема тела

Для начала, рассмотрим, как работает формула, которая позволяет рассчитать скорость подъема тела, брошенного вверх с поверхности Земли. Данная формула описывает движение тела в вертикальном направлении под действием силы тяжести:

v = v₀ — gt

где:

v – скорость тела в момент времени t;
v₀ – начальная скорость тела;
g – ускорение свободного падения, постоянное значение, равное на поверхности Земли 9,8 м/c²;
t – время движения тела в вертикальном направлении.

Из формулы видно, что скорость тела уменьшается пропорционально времени движения, при этом ускорение свободного падения на поверхности Земли остается постоянным.

Решение задачи на примере

Рассмотрим пример, чтобы проиллюстрировать, как работает данная формула и как найти скорость подъема тела, брошенного вверх с поверхности Земли. Пусть мы бросили мяч вертикально вверх со скоростью 15 м/c. На какой высоте от поверхности Земли мяч потеряет скорость, а затем начнет двигаться вниз со скоростью 15 м/c?

Для начала найдем время, за которое мяч остановится на высоте h:

15 – 9.8t = 0

t = 1.53 с

Теперь найдем высоту h:

h = v₀t — 1/2gt²

h = 15*1.53 — 1/2*9.8*1.53²

h = 11.39 м

Таким образом, на высоте 11.39 м от поверхности Земли мяч потеряет свою начальную скорость и будет двигаться вниз со скоростью 15 м/c.

Методы расчета скорости подъема

Существуют различные методы расчета скорости подъема тела, брошенного вверх с поверхности Земли:

Метод использования полной энергии:

При этом методе используется закон сохранения энергии для получения скорости подъема тела. При броске тела вверх его начальная кинетическая энергия преобразуется в потенциальную энергию на высоте максимального подъема. Следовательно, максимальная высота подъема мяча может быть вычислена при помощи формулы:

h = (v₀²) / (2g)

Закон сохранения энергии может быть использован для нахождения скорости подъема мяча на высоте максимального подъема:

v = (2gh)^(1/2)

Метод использования времени полета:

Для получения скорости подъема мяча можно использовать закон движения тела, используя время полета и максимальную высоту подъема. Следовательно, для нахождения скорости подъема мяча при помощи времени полета необходимо знать максимальную высоту подъема мяча и время полета:

v = h / t

Метод использования уравнения пути:

Для нахождения скорости подъема мяча можно использовать уравнение пути. Это уравнение описывает движение тела с учетом времени и начальной скорости. Следовательно, для нахождения скорости подъема мяча необходимо знать максимальную высоту подъема мяча и время полета:

v = (h — 1/2gt²)^(1/2)

Итог

Таким образом, мы рассмотрели, как найти скорость подъема тела, брошенного вверх с поверхности Земли, при помощи формулы подъема тела. Для этого можно использовать различные методы расчета, включая метод использования полной энергии, метод использования времени полета и метод использования уравнения пути. Каждый метод имеет свои преимущества и недостатки, поэтому необходимо определить конкретный метод в зависимости от поставленной задачи.

Как найти скорость подъема тела с поверхности земли брошенного вверх

Бросание предметов вверх является одним из классических экспериментов в физике. Изучение движения тела может быть полезно не только для школьников, но и для профессионалов, занимающихся наукой или инженерией. Одним из важных аспектов движения тела является его скорость.

Что такое скорость подъема тела?

Скорость подъема тела — это скорость, с которой тело движется вверх относительно поверхности земли. Она измеряется в метрах в секунду и обычно является положительным числом. Если тело движется вниз, то его скорость будет отрицательной.

Как вычислить скорость подъема тела?

Существует несколько способов вычисления скорости подъема тела, но мы рассмотрим два наиболее распространенных:

Метод 1: Использование уравнения движения тела для свободного падения

Этот метод требует знаний в области физики и общей кинематики. Сначала мы должны установить высоту, на которой было брошено тело, и время, за которое оно поднялось на максимальную высоту и затем вернулось обратно на землю. Это можно измерить с помощью специального оборудования, такого как камера со замедленной съемкой, или подсчета времени вручную. Затем мы можем использовать уравнение свободного падения:

h = V₀t + ½gt²

где:

h — максимальная высота, достигнутая телом
V₀ — начальная скорость (в данном случае, скорость броска, которая равна 0)
t — время, за которое тело поднимается на максимальную высоту и возвращается обратно на землю
g — ускорение свободного падения, примерно равное 9,8 м/с²

Решив уравнение относительно скорости (V₀), мы можем найти значение скорости, с которой тело было брошено вверх:

V₀ = (h — ½gt²) / t

Метод 2: Использование максимальной высоты, достигнутой телом

Этот метод требует меньше знаний в области физики и более доступен для людей без специального образования. Мы можем измерить максимальную высоту, достигнутую телом, и затем использовать формулу для вычисления времени подъема:

t = √(2h / g)

где:

h — максимальная высота, достигнутая телом
g — ускорение свободного падения, примерно равное 9,8 м/с²

После нахождения времени подъема мы можем использовать уравнение движения для свободного падения, чтобы найти скорость подъема тела:

V = gt

Пример расчета скорости подъема тела

Рассмотрим простой пример. Какова скорость подъема тела, если его бросили вверх с высоты 10 м и он достиг максимальной высоты через 2 секунды?

Метод 1:

Используем уравнение движения тела для свободного падения:

h = V₀t + ½gt²

Решим уравнение относительно скорости (V₀):

V₀ = (h — ½gt²) / t = (10 — ½ * 9,8 * 2²) / 2 = 0 м/с

Скорость броска (V₀) равна нулю, так как в начальный момент тело находится в покое.

Метод 2:

Используем формулу для вычисления времени подъема:

t = √(2h / g) = √(2 * 10 / 9,8) = 1,43 с

Используем уравнение движения для свободного падения, чтобы найти скорость подъема тела:

V = gt = 9,8 * 1,43 = 14,03 м/с

Вывод

Расчет скорости подъема тела, брошенного вверх, может иметь много применений, включая спорт, науку и инженерию. Существует несколько методов для вычисления этой скорости, в том числе метод, основанный на уравнениях движения тела для свободного падения, и метод, основанный на максимальной высоте, достигнутой телом. Независимо от метода, точный расчет скорости подъема тела может помочь улучшить производительность, повысить безопасность и обогатить наши знания в области физики.

Источник

Движение тела, брошенного под углом к горизонту, — движение тела в двумерной системе координат (по двум осям) при изначальном направлении начальной скорости под углом к горизонту. Данное движение является сложным видом механического движения с криволинейной траекторией. Такие типы движений принято рассматривать в проекции на оси выбранной системы координат. В нашем конкретном случае возьмём декартову систему координат и запустим тело под углом displaystyle alpha к оси ОХ (рис. 1).

Рис. 1. Тело бросили под углом к горизонту

Классическая постановка задач на подобную тематику: тело бросили под углом $displaystyle {{upsilon }_{0}}$ к горизонту с начальной скоростью $displaystyle {{upsilon }_{0}}$ , найти различные параметры движения.

Первое, что мы сделаем, это попробуем данное сложное движение представить как сумму простых (рис. 2).

Рис. 2. Тело бросили под углом к горизонту (максимальная высота подъёма, путь по горизонтали, движение)

Рассмотрим само движение. После броска траектория движущегося тела представляет собой параболу (докажем позже). Выберем произвольную точку на параболе и укажем ускорение, с которым движется тело в данный момент (ускорение свободного падения). Направление данного ускорения — вертикально вниз. Проекции данного ускорения на ось ОХ ( $displaystyle {{c}^{2}}$ (м/ $displaystyle {{g}_{y}}=-10$ ), а на ось OY ( $displaystyle {{c}^{2}}$ (м/ $displaystyle {{c}^{2}}$ ).

Тогда, вдоль оси ОХ, тело движется равномерно (т.к. ускорение вдоль этой оси равно 0). Более сложным является движение тела вдоль оси OY: между точками A и B тело движется замедляясь, при этом движение равнозамедленное. Между точками B и C движение равноускоренное (рис.2, подписи). Исходя из установленного вида движения, можем решать задачу.

Рис. 3. Тело бросили под углом к горизонту (проекции скоростей)

Для рассмотрения движения тела вдоль осей, введём начальные скорости движения тела вдоль выбранных нами осей (рис. 3). На рисунке представлена часть траектории в самом начале движения. Начальные скорости движения вдоль осей обозначим $displaystyle {{upsilon }_{0y}}$ и $displaystyle left| {{{vec{upsilon }}}_{0}} right|$ . Исходя из треугольника, катетами которого являются наши проекции (можно построить параллельным переносом), а гипотенузой — модуль вектора начальной скорости ( $displaystyle left| {{{vec{upsilon }}}_{0}} right|$ ), можем найти значения необходимых нам проекций:

$displaystyle {{upsilon }_{0x}}={{upsilon }_{0}}cos alpha$ (1)
$displaystyle {{upsilon }_{0y}}={{upsilon }_{0}}sin alpha$ (2)

Вернёмся к рисунку 2. Попробуем найти полное время полёта ( $displaystyle {{t}_{max }}$ ). Для этого воспользуемся тем, что вдоль оси OY тело движется равнозамедленно, а в точке B движение вдоль этой оси и вовсе останавливается. Таким образом, конечная скорость в этой точке вдоль оси OY равна 0. Тогда, исходя из движения:

$displaystyle 0={{upsilon }_{0y}}-gfrac{{{t}_{max }}}{2}$ (3)

$displaystyle frac{{{t}_{max }}}{2}$ — т.к. время движения от точки А до B, и от B до C одинаково. Тогда:

$displaystyle {{t}_{max }}=frac{2{{upsilon }_{0y}}}{g}$ (4)

И, учитывая (2):

$displaystyle {{t}_{max }}=frac{2{{upsilon }_{0}}sin alpha }{g}$ (5)

Перейдём к вопросу о максимальной дальности броска в горизонтальном направлении ( $displaystyle {{S}_{max }}$ ).

Вдоль горизонта тело движется равномерно (рис. 2). Тогда путь, проделанный телом за время $displaystyle {{t}_{max }}$ :

$displaystyle {{S}_{max }}={{upsilon }_{0x}}{{t}_{max }}$ (6)

А с учётом (1) и (5):

$displaystyle frac{2upsilon _{0}^{2}sin alpha cos alpha }{g}$ = $displaystyle frac{upsilon _{0}^{2}sin (2alpha )}{g}$ = $displaystyle frac{upsilon _{0}^{2}sin (2alpha )}{g}$ (7)

Перейдём к максимальной высоте полёта ( $displaystyle {{H}_{max }}$ ). Данный параметр связан с движением тела вдоль оси OY, которое, как мы выяснили, является равноускоренным/равнозамедленным. Рассмотрим участок BC: для него вдоль соответствующей оси тело без начальной скорости движется с ускорением ( $displaystyle frac{{{t}_{max }}}{2}$ ) в течение времени $displaystyle frac{{{t}_{max }}}{2}$ , формируем уравнение:

$displaystyle {{H}_{max }}=frac{g{{left( {}^{{{t}_{max }}}!!diagup!!{}_{2}; right)}^{2}}}{2}=frac{g{{left( {{t}_{max }} right)}^{2}}}{8}$ (8)

С учётом (5):

$displaystyle frac{upsilon _{0}^{2}{{sin }^{2}}alpha }{2g}$ = $displaystyle frac{upsilon _{0}^{2}{{sin }^{2}}alpha }{2g}$ (9)

Таким образом, ряд параметров движения при броске под углом к горизонту можно вычислить, зная лишь начальные параметры броска.

Рис. 4. Тело бросили под углом к горизонту (конечная скорость)

Далее попробуем найти конечную скорость движения (при таких движениях, конечная скорость — скорость при подлёте к Земле). Рассмотрим конечную точку движения С (рис. 4). Скорость тела направлена под неким углом displaystyle beta . Построим проекции данного вектора на оси OX и OY. На основании построенного треугольника реализуем теорему Пифагора для поиска модуля полной конечной скорости:

$displaystyle left| {vec{upsilon }} right|=sqrt{upsilon _{x}^{2}+upsilon _{y}^{2}}$ (10)

Найдём компоненты вектора displaystyle left| {vec{upsilon }} right| . Т.к. движение вдоль оси OX равномерное, значит, $displaystyle {{upsilon }_{x}}={{upsilon }_{0x}}$ , используя (1):

$displaystyle {{upsilon }_{x}}={{upsilon }_{0}}cos alpha$ (11)

Движение вдоль оси OY от точки B в точку C равноускоренное, причём, без начальной скорости за время $displaystyle frac{{{t}_{max }}}{2}$ , тогда:

$displaystyle {{upsilon }_{y}}=gfrac{{{t}_{max }}}{2}$ (12)

Используя (5), получим:

$displaystyle {{upsilon }_{y}}=gfrac{2{{upsilon }_{0}}sin alpha }{2g}={{upsilon }_{0}}sin alpha$ (13)

Подставим (12) и (13) в (10):

$displaystyle {{upsilon }_{0}}sqrt{{{(cos alpha )}^{2}}+{{(sin alpha )}^{2}}}$ = $displaystyle {{upsilon }_{0}}$ = $displaystyle {{upsilon }_{0}}$ (14)

Для избавления от тригонометрических функций мы воспользовались основным тригонометрическим тождеством. Таким образом, доказано, что конечная скорость такого движения равна начальной, кроме того, из треугольника видно, что тело подлетело к земле под углом displaystyle beta =alpha .

Вывод:

для движения тела, брошенного под углом к горизонту, выведены добавочные формулы: (5), (7), (9), которые могут существенно упростить решение задачи.
представлен один из общих способов нахождения скорости при криволинейном движении (через теорему Пифагора и поиск компонент вектора).

Источник

Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.

Важные факты!График движения тела, брошенного под углом к горизонту:

α — угол, под которым было брошено тело

Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v_0x = v₀cosα. Ее проекция на ось ОУ равна v_0y = v₀sinα.
Проекция мгновенной скорости на ось ОХ равна: v_x = v₀cosα. Ее проекция на ось ОУ равна нулю: v_y = v₀sinα – gt.
Проекция ускорения свободного падения на ось ОХ равна нулю: g_x = 0. Ее проекция на ось ОУ равна –g: g_y = –g.

Кинематические характеристики

Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:

Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:

v_min = v₀cosα = v_h

Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:

v_max = v_o = v

Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: v_y = 0. Время подъема определяется следующей формулой:

Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:

Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:

l = s_x = v_0xt_полн = v₀cosα t_полн

Подставляя в выражение формулу полного времени полета, получаем:

Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:

Учитывая, что x₀ = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v₀cosα, данная формула принимает вид:

x = v₀cosα t

Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:

Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v₀sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:

Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:

Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?

Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:

v₀sinα = gt_под

Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:

Тело, брошенное под углом к горизонту с некоторой высоты

Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.

Важные факты!

График движения тела, брошенного под углом к горизонту с некоторой высоты:

Время падения тела больше времени его подъема: t_пад > t_под.

Полное время полета равно:

t_полн = t_пад + t_под

Уравнение координаты x:

x = v₀cosα t

Уравнение координаты y:

Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.

Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:

x = v₀cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.

Задание EF17562

С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.

Алгоритм решения

1.Записать исходные данные.

2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.

3.Выбрать нулевой уровень для определения потенциальной энергии.

4.Записать закон сохранения энергии.

5.Решить задачу в общем виде.

6.Подставить числовые значения и произвести вычисления.

Решение

Запишем исходные данные:

• Время падения стального шарика: t = 0,4 c.

• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.

• Угол наклона плиты: α = 30^о.

Построим чертеж и укажем на нем все необходимое:

Нулевой уровень — точка D.

Закон сохранения энергии:

E_k0 + E_p0 = E_k + E_p

Потенциальная энергия шарика в точке А равна:

E_pA = mgH

Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.

В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:

EpB=mgl1

Перед ударом кинетическая энергия шарика равна:

EkB=mv22

Согласно закону сохранения энергии:

EpA=EpB+EkB

mgH=mgl1+mv22

Отсюда высота H равна:

H=mgl1mg+mv22mg=l1+v22g

Относительно точки В шарик поднимется на высоту h – l₁. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:

h−l1=v2sin2β2g=v2sin2(90−2α)o2g

Отсюда:

l1=h−v2sin2(90−2α)o2g

Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:

v=gt

Следовательно:

H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g

H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)

H=1,4−10·0,422(sin2(90−60)o−1)

H=1,4−5·0,16(sin230o−1)

H=1,4−0,8((12)2−1)=1,4−0,8(14−1)

H=1,4+0,6=2 (м)

Ответ: 20

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17980

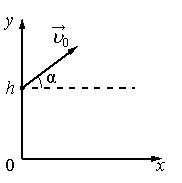
В момент t=0 мячик бросают с начальной скоростью v₀ под углом α к горизонту с балкона высотой h (см. рисунок).

Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).

К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.

Алгоритм решения

Установить вид механического движения, исходя из условий задачи.
Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
Определить, как зависят эти величины от времени.
Установить соответствие между графиками и величинами.

Решение

Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.

Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.

Координата x меняется согласно уравнению координаты x:

Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:

Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:

В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.

Формула проекции скорости мячика на ось ОХ:

Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.

Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.

Остается последний вариант — координата y. Уравнение этой координаты имеет вид:

Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.

Теперь записываем установленные соответствия в порядке АБ: 42.

Ответ: 42

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18741

Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?

Для каждой величины определите соответствующий характер изменения:

увеличивается
уменьшается
не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Сделать чертеж, иллюстрирующий ситуацию.
Записать формулы, определяющие указанные в условии задачи величины.
Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.

Решение

Выполняем чертеж:

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).

Горизонтальная составляющая скорости шарика определяется формулой:

v_x = v₀ cosα

Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).

Ответом будет следующая последовательность цифр — 33.

Ответ: 33

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 42.8k

Источник

Общее время движения

Дальность полета

Максимальная высота подъёма тела

Задачи

Список литературы

Как найти скорость подъема тела с поверхности земли брошенного вверх?

Шаг 1. Определите начальную скорость тела.

Шаг 2. Найдите время подъема тела.

Шаг 3. Определите высоту, на которую было брошено тело.

Шаг 4. Определите скорость тела на максимальной высоте.

Шаг 5. Найдите скорость тела на любой другой высоте.

В заключение

Как найти скорость подъема тела с поверхности земли брошенного вверх

Как работает формула подъема тела

Решение задачи на примере

Методы расчета скорости подъема

Итог

Как найти скорость подъема тела с поверхности земли брошенного вверх

Что такое скорость подъема тела?

Как вычислить скорость подъема тела?

Пример расчета скорости подъема тела

Вывод

Кинематические характеристики

Тело, брошенное под углом к горизонту с некоторой высоты

Вам также может понравиться

Как найти свой авто по гос номеру

Как найти тромб у человека

Что делать если вытягивается рассада капусты как исправить

Добавить комментарий Отменить ответ