Как найти время заряда конденсатора

Думаете все так сложно? А давайте проверим.

Для начала нам нужно знать, что конденсатор накапливает электрический заряд между своими обкладками. Более подробно как это происходит с физической точки зрения можно прочесть в книжках. Для нас сейчас главное понимать его предназначение.

Если подключить к его выводам источник тока, то на обкладках начнет накапливаться разноименный заряд. Важно помнить, что величина заряда одинаковая но разная по полярности.

Емкость есть. Если последовательно с ней подключен резистор, то можно посчитать время за которое зарядится любой конденсатор.

Тут кроется небольшая уловка. Конденсатор заряжается не с постоянной скоростью. Подключив конденсатор к источнику тока с напряжением в 12 Вольт, напряжение в 1В он наберет очень быстро, 2В уже медленнее, 3В уже дольше и так к примеру до 12В.

Величина, которая это описывает называется постоянная времени:

читается как постоянная времени равняется произведению сопротивления в Омах и емкости в Фарадах.

Для примера давайте возьмем цепь состоящую из резистора номиналом 1кОм = 1000 Ом и конденсатора емкостью 1000 мкФ = 0.001Ф. Мы сразу переводим все в Омы и Фарады для расчетов:

Постоянная времени = 1000 х 0.001 = 1;

Что такое 1? Конденсатор зарядится полностью за 1 секунду? – Нет. Это постоянная времени. Она показывает за какое время наш конденсатор наберет 63% от величины напряжения подключенного на него источника. При условии, что до подключения наш конденсатор был полностью разряжен и имел напряжение на обкладках равное 0В.

Почему 63% спросите вы? Так посчитали и вывели. Для более детального разъяснения обратитесь к учебникам ВУЗов.

Значит выяснили, что постоянная времени – это время, за которое наш конденсатор заряжается до 63% от разности между источником питания и напряжением на обкладках.

Так в первую секунду постоянной времени = 1, наш конденсатор зарядится на 63% в течении 1 сек., когда значение постоянной времени = 2, наш конденсатор зарядится до значения в 63% от напряжения источника тока за 2 сек. Это можно продолжать долго. Но суть остается одна, увеличивая постоянную времени, мы изменяем время заряда конденсатора.

Если продолжать и дальше заряжать конденсатор, то произойдет следующий заряд на 63% от оставшейся разности напряжений, между его текущим значением напряжения и напряжением источника тока.

В идеальной вселенной процесс заряда емкости до своего максимального значения может продолжаться очень долго – бесконечно. Но так как у нас все же реальный мир из неидеальных компонентов, то мы можем говорить о том, что емкость зарядится до своего максимума уже при:

Поэтому, можно смело говорить о том, что уже по прошествии 5 х постоянную времени сек., после включения питания, наш конденсатор будет иметь практически полный заряд равный 99% своей емкости.

Главное уловить суть, как заряжается конденсатор. Заряд происходит, как показано на рис.2, условием к данному примеру считать напряжение питания 12В, постоянная времени = 1 сек.:

Немного пояснений:

0 сек. – на обкладках нет напряжения;

1 сек. – постоянная времени равна 1 сек, заряд конденсатора равен 63% от 12В = 7,56В.

2 сек. – постоянная времени равна 2 сек, заряд конденсатора равен:

12В – 7.56В = 4.44В (отнимаем от приложенного напряжения, значение уже имеющегося напряжения на обкладках конденсатора)

4.44 х 0.63 = 2,8 В (высчитываем, какое напряжение от 4.44В будет на долю 63%)

7.56В + 2,8В = 10,36В (напряжение на конденсаторе после 2 сек.)

3 сек. – постоянная времени равна 3 сек, заряд конденсатора равен:

12В – 10.36 = 1,64В (отнимаем от приложенного напряжения, значение уже имеющегося напряжения на обкладках конденсатора)

1,64 х 0,63 = 1,03В (высчитываем, какое напряжение от 1,64В будет на долю 63%)

10,36В + 1,03В = 11,39В (напряжение на конденсаторе после 3 сек.)

Дальше не вижу смысла расписывать, суть вы уловили.

В результате на 5 секунде мы будем иметь практически равное источнику питания напряжение на обкладках конденсатора.

Спасибо, что дочитали статью до конца!

Подписывайтесь на канал РОБОТИП впереди много интересного!

• 

Время заряда конденсатора

Время заряда конденсатора зависит от первоначального напряжения и емкости самого накопителя, ЭДС источника тока, сопротивления всех участков электрической цепи.

Конденсатор

Конденсатор – устройство для накопления электрического заряда, состоящее из двух и более проводников (обкладок), разделенных диэлектриком. По предназначению он напоминает батарейку.

Если замкнуть цепь с заряженным конденсатором, он будет отдавать энергию и разряжаться, потечет ток. Когда же он разрядится полностью, поток электронов останавливается.

Главной характеристикой конденсатора является емкость (С), т.е. способность накапливать электрический заряд. Она определяется отношением этого показателя (Q) к напряжению (U):

С = Q/U

Время, необходимое для зарядки конденсатора

В идеальных условиях, когда источник напряжения мощный, нет препятствий потоку электричества, конденсатор безупречен, время зарядки конденсатора будет равно 0.

На практике же на каждом участке цепи существует явное (резисторы) или неявное (провода, источник напряжения и т.п.) сопротивление. В этом случае время заряда конденсатора будет зависеть от сопротивления во всей цепи и его емкости.

В самом начале заряда на обкладках накопителя много свободного места, напряжение равно нулю. Начальный ток в этот момент максимален. По мере заполнения конденсатора заряженными частицами их поток постепенно снижается, U растет все медленнее. Когда не останется свободного места на обкладках, ток прекратится, напряжение станет максимальным и равным таковому источника.

Экспонента увеличения энергии в конденсаторе изображена на рисунке. Сама формула зависимости нарастания напряжения от времени заряда имеет следующий вид:

U=Uc*[1-e^(-t/τ)]

где Uс – электродвижущая сила источника, t – время заряда, τ – постоянная времени, равная R*C (R – сопротивление).

За время τ зарядка конденсатора дойдет до (1 – 1/e)*100% ≈ 63% от U.

За 3τ – до (1 – 1/e³)*100% ≈ 95% от U.

За 5τ – до (1 – 1/e⁵)*100% ≈ 99% от U.

Время заряда конденсатора точно до уровня напряжения источника длится бесконечно долго.

Из вышеприведенной формулы вычисления напряжения можно вывести расчет времени зарядки накопителя до определенных показателей:

t = – ln (1 – U/Uc) * RC

Калькулятор расчета времени зарядки конденсатора до 99.2% и других ее параметров от источника постоянной ЭДС приведен на сайте planetcalc.ru

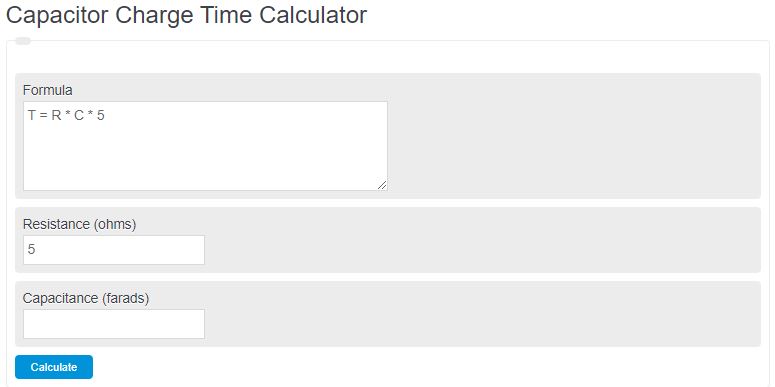
Unit Converter

Enter the resistance in ohms and capacitance in farads into the calculator to determine the total time to charge a capacitor.

• RC Time Constant Calculator
• Battery Run Time Calculator
• Capacitor Discharge Calculator
• Capacitance Calculator
• Capacitor Size Calculator

The following formula can be used to calculate the charge time of a capacitor.

• Where T is the time (seconds)
• R is the resistance (ohms)
• C is the capacitance (farads)

To calculate the capacitor charge time in seconds, multiply the resistance by the capacitance, then again by 5.

Capacitor Charge Time Definition

A capacitor charge time is defined as the time it takes a capacitor to charge to 99%. This value is equal to 5 capacitor time constants.

Capacitor Charge Time Example

How to calculate capacitor charge time?

1. First, determine the resistance.

   Measure the resistance of the capacitor.

2. Next, determine the capacitance.

   Calculate the capacitance of the capacitor.

3. Finally, calculate the charge time.

   Calculate the capacitor charge time using the equation above.

FAQ

How long does a capacitor take to charge?

A capacitor will reach a 99% charge after 5-time constants and 63.2% after just one time constant. The time constant is calculated using the formula t = R*C. Typically either 4 or 5-time constants a capacitor is considered a full charge. (It will never reach 100% charge.

How long does a capacitor take to discharge?

Conversely, a capacitor will discharge only 36.8% after one time constant, but also reach near 99% discharge at around 5-time constants.

Время заряда конденсатора

Время заряда конденсатора зависит от первоначального напряжения и емкости самого накопителя, ЭДС источника тока, сопротивления всех участков электрической цепи.

Конденсатор

Конденсатор – устройство для накопления электрического заряда, состоящее из двух и более проводников (обкладок), разделенных диэлектриком. По предназначению он напоминает батарейку.

Если замкнуть цепь с заряженным конденсатором, он будет отдавать энергию и разряжаться, потечет ток. Когда же он разрядится полностью, поток электронов останавливается.

Главной характеристикой конденсатора является емкость (С), т.е. способность накапливать электрический заряд. Она определяется отношением этого показателя (Q) к напряжению (U):

Время, необходимое для зарядки конденсатора

В идеальных условиях, когда источник напряжения мощный, нет препятствий потоку электричества, конденсатор безупречен, время зарядки конденсатора будет равно 0.

На практике же на каждом участке цепи существует явное (резисторы) или неявное (провода, источник напряжения и т.п.) сопротивление. В этом случае время заряда конденсатора будет зависеть от сопротивления во всей цепи и его емкости.

В самом начале заряда на обкладках накопителя много свободного места, напряжение равно нулю. Начальный ток в этот момент максимален. По мере заполнения конденсатора заряженными частицами их поток постепенно снижается, U растет все медленнее. Когда не останется свободного места на обкладках, ток прекратится, напряжение станет максимальным и равным таковому источника.

Экспонента увеличения энергии в конденсаторе изображена на рисунке. Сама формула зависимости нарастания напряжения от времени заряда имеет следующий вид:

где Uс – электродвижущая сила источника, t — время заряда, τ — постоянная времени, равная R*C (R — сопротивление).

За время τ зарядка конденсатора дойдет до (1 — 1/e)*100% ≈ 63% от U.

За 3τ — до (1 — 1/e 3 )*100% ≈ 95% от U.

За 5τ — до (1 — 1/e 5 )*100% ≈ 99% от U.

Время заряда конденсатора точно до уровня напряжения источника длится бесконечно долго.

Из вышеприведенной формулы вычисления напряжения можно вывести расчет времени зарядки накопителя до определенных показателей:

Источник

Конденсатор в цепи постоянного тока

Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление.

Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление. Формулы, по которым идет расчет, приведены под калькуляторами.

Заряд конденсатора от источника постоянной ЭДС

Разряд конденсатора через сопротивление

Понять приводимые ниже формулы поможет картинка, изображающая электрическую схему заряда конденсатора от источника постоянной ЭДС (батареи):

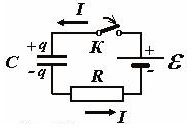
Итак, при замыкании ключа К в цепи пойдет электрический ток, который будет приводить к заряду конденсатора.
По закону Ома сумма напряжений на конденсаторе и резисторе равна ЭДС источника, таким образом:

При этом заряд и сила тока зависят от времени. В начальный момент времени на конденсаторе нет заряда, сила тока максимальна, также как и максимальна мощность, рассеиваемая на резисторе.

Во время зарядки конденсатора, напряжение на нем изменяется по закону

где величину

называют постоянной времени RC-цепи или временем зарядки конденсатора.
Вообще говоря, согласно уравнению выше, заряд конденсатора бесконечно долго стремится к величине ЭДС, поэтому для оценки времени заряда конденсатора используют величину
— это время, за которое напряжение на конденсаторе достигнет значения 99,2% ЭДС.
Заряд на конденсаторе:

Энергия, запасенная в конденсаторе:

Работа, выполненная источником ЭДС:

Источник

Заряд и разряд конденсатора

Значение диэлектрика

Кроме общего размера обкладок и расстояния между ними, существует ещё один параметр, влияющий на ёмкость — используемый тип изолятора. Фактор, по которому определяется способность диэлектрика повышать ёмкость конденсатора в сравнении с вакуумом, называется диэлектрической проницаемостью и описывается для разных материалов постоянной величиной от 1 и до бесконечности (теоретически):

• вакуум: 1,0000;
• воздух: 1,0006;
• бумага: 2,5—3,5;
• стекло: 3—10;
• оксиды металлов 6—20;
• электротехническая керамика: до 80.

Кроме конденсаторов с твёрдым диэлектриком (керамических, бумажных, плёночных) существуют также электролитические. В последних используют алюминиевые или танталовые пластины с оксидным изолирующим слоем в качестве одного электрода и раствор электролита в качестве другого.

Энергия, которую способны накопить большинство конденсаторов, обычно невелика — не больше сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому конденсаторы не могут заменить, например, аккумуляторные батареи в качестве источника питания. И хотя они способны эффективно выполнять только одну работу (сохранение заряда), их применение весьма многообразно в электрических цепях. Конденсаторы используются как фильтры, для сглаживания сетевого напряжения, в качестве устройств синхронизации и для других целей.

Синтаксис

Для пользователей XMPP клиентов, используется команда

где ключи это известные параметры, параметра=значение, разделенные точкой с запятой

Обязателен ключ key=razryad при расчете разаряда конденсатора

и zaryad при расчете заряда

Так как при других параметрах ключах будут рассчитываться совершенно другие формулы. Например баллистического движения или давления над уровнем моря.

Заметьте, чем данный калькулятор отличается от других:

Во первых: данные можно вводить не переводя из наноФарад в Фарады, а килоОмы в Омы. Если уж заданы параметры в единицах измерения то так и пишите. Если не напишите то считается что данные заданы в основным единицах СИ ( то есть метр, Фарад, Ом)

Во вторых: Расчет ведётся по тем параметрым которые можно рассчитать зная исходные.Это очень удобно, когда нужно рассчитать любой из параметров в формуле, когда известны все остальные. Другие известные калькуляторы могут рассчитывать только по определенному алгоритму и только в одну сторону.

Разряд конденсатора

После того как конденсатор зарядился, отключим источник питания и подключим нагрузку R. Так как конденсатор уже заряжен, он сам превратился в источник питания. Нагрузка R образовала проход между пластинами. Отрицательно заряженные электроны, накопленные на одной пластине, согласно силе притяжения между разноименными зарядами, двинутся в сторону положительно заряженных ионов на другой пластине.

В момент подключения R, напряжение на конденсаторе то же, что и после окончания переходного периода зарядки. Начальный ток по закону Ома будет равняться напряжению на обкладках, разделенном на сопротивление нагрузки.

Как только в цепи пойдет ток, конденсатор начнет разряжаться. По мере потери заряда, напряжение начнет падать. Следовательно, ток тоже упадет. По мере понижения значений напряжения и тока, будет снижаться их скорость падения.

Время зарядки и разрядки конденсатора зависит от двух параметров – емкости конденсатора C и общего сопротивления в цепи R. Чем больше емкость конденсатора, тем большее количество заряда должно пройти по цепи, и тем больше времени потребует процесс зарядки/разрядки ( ток определяется как количество заряда, прошедшего по проводнику за единицу времени). Чем больше сопротивление R, тем меньше ток. Соответственно, больше времени потребуется на зарядку.

Продукт RC (сопротивление, умноженное на емкость) формирует временную константу ? (тау). За один ? конденсатор заряжается или разряжается на 63%. За пять ? конденсатор заряжается или разряжается полностью.

Для наглядности подставим значения: конденсатор емкостью в 20 микрофарад, сопротивление в 1 килоом и источник питания в 10В. Процесс заряда будет выглядеть следующим образом:

Заряд конденсатора. Ток

По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.

Рассмотрим принцип работы плоского конденсатора. Если подключить к нему источник питания, на одной пластине проводника начнут собираться отрицательно заряженные частицы в виде электронов, на другой – положительно заряженные частицы в виде ионов. Поскольку между обкладками находиться диэлектрик, заряженные частицы не могут «перескочить» на противоположную сторону конденсатора. Тем не менее, электроны передвигаются от источника питания — до пластины конденсатора. Поэтому в цепи идет электрический ток.

В самом начале включения конденсатора в цепь, на его обкладках больше всего свободного места. Следовательно, начальный ток в этот момент встречает меньше всего сопротивления и является максимальным. По мере заполнения конденсатора заряженными частицами ток постепенно падает, пока не закончится свободное место на обкладках и ток совсем не прекратится.

Время между состояниями «пустого» конденсатора с максимальным значением тока, и «полного» конденсатора с минимальным значением тока (т.е. его отсутствием), называют переходным периодом заряда конденсатора.

Формула

Нахождение тока конденсаторного заряда происходит по формуле, представленной ниже. Измеряется он в фарадах, что равно кулону или вольту.

Формула нахождения заряда конденсатора

В целомэто элемент электросети, накапливающий и сохраняющий напряжение в ней. Бывает разного типа и размера, к примеру, электролитическим, керамическим и танталовым. Состоит, в основном, из нескольких токопроводящих обкладок с диэлектриком. Его емкость зависит от размеров диэлектрика и заполнителя между обкладками. Заряжается благодаря электричеству. Определить ток конденсаторного заряда можно измерительными приборами и формулой.

Устройство и принцип работы

В простейшем варианте конструкция состоит из двух электродов в форме проводящих пластин (называемых обкладками), разделённых диэлектриком, толщина которого ничтожно мала по сравнению с размерами обкладок. Практически применяемые радиоэлектронные компоненты содержат много слоёв диэлектрика и электродов. В качестве обозначения конденсатора на схеме используются два параллельных отрезка с пространством между ними. Они символизируют металлические пластины обкладок физического прибора, электрически разделённые между собой.

Многие считают Майкла Фарадея автором изобретения, но на самом деле это не так. Но он сделал главное — продемонстрировал первые практические примеры и способы использования этого прибора для хранения электрического заряда в своих экспериментах. Благодаря Фарадею человечество получило способ измерять возможность накапливать заряд. Эта величина называется ёмкостью и измеряется в Фарадах.

Работу конденсатора можно проиллюстрировать на примере событий, проходящих во вспышке цифровой фотокамеры за отрезок времени между нажатием кнопки и тем моментом, когда вспышка погаснет. Основой электронной схемы этого осветительного устройства является конденсатор, в котором происходит следующее:

• Зарядка. После нажатия кнопки поток электронов приходит в конденсатор и останавливается на одной из его пластин благодаря диэлектрику. Этот поток называется зарядным током.
• Накопление. Поскольку под действием электродвижущей силы всё больше и больше электронов будут поступать на обкладку и распределяться по ней, отрицательный заряд обкладки может расти до момента, пока накопленный потенциал не будет отталкивать поступающий избыточный поток электронов. Вторая пластина из-за дефицита электронов приобретает положительный заряд, по модулю равный отрицательному на первой. Зарядный ток будет протекать до тех пор, пока напряжение на обеих пластинах не сравняется с приложенным. Сила или скорость тока зарядки будет находиться на максимальном уровне в момент, когда пластины полностью разряжены, и приблизится к нулю в момент, когда напряжение на обкладках и источнике будут равны.
• Сохранение. Поскольку обкладки заряжены противоположно, ионы и электроны будут притягиваться друг к другу, но не смогут соединиться из-за диэлектрической прослойки, создавая электростатическое поле. Благодаря этому полю конденсатор удерживает и сохраняет заряд.
• Разряд. Если в цепи появляется возможность для электронов протечь другим путём, то напряжение, накопленное между положительными и отрицательными зарядами обкладок, мгновенно реализуется в электрический ток, импульс которого в лампе вспышки преобразуется в световую энергию.

Определение заряда

Определить, заряжен ли проводник, можно специальным измерительным прибором. К примеру, сделать это можно при помощи индикаторной отвертки. При разряде избыточные виды электронов, имеющих левую пластину, будут перемещены через некоторое время по проводам к правой части пластины, то есть они будут смещены к местам, где их недостаточно.

Обратите внимание! Когда число электронов будет одинаковым, то разряд прекратится и проводная энергия вместе с сопротивлением исчезнет. Использование измерительного оборудования для определения конденсаторного заряда

Использование измерительного оборудования для определения конденсаторного заряда

Процессы зарядки и разрядки конденсаторов.

С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:

Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?

Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:

В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.

Как видите, здесь нет ничего сложного

Относительная диэлектрическая проницаемость

Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме.

Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации – смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.

Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.

Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.

Бумага – от 2.5 до 3.5

Стекло – от 3 до 10

Слюда – от 5 до 7

Порошки оксидов металлов – от 6 до 20

Плоский конденсатор.

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:

Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.

Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:

Каждая из обкладок конденсатора в отдельности создает электрическое поле:

• положительно заряженная пластина (+q) создает поле, напряженность которого равна E_
• отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_

Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:

Здесь sigma– это поверхностная плотность заряда: sigma = frac, а varepsilon – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:

Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:

А какая же будет величина напряженности вне конденсатора? А все просто – слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0

От чего зависит емкость

Емкость это свойство накопления и удержания электрозаряда. Чем она больше, тем больше заряд, увеличивающий вместимость сосуда с газовым баллоном. Она зависит от того, какова форма и размер электродов. Также зависит от того, какое расположение и свойство имеет диэлектрик, разделяющий электрод. Есть плоский конденсаторный источник с параллельной и цилиндрической пластиной.

Имеет не только специально предусмотренное устройство, но и несколько проводников, которые разделены при помощи диэлектрика. Емкость существенно влияет на электротехнические установки переменного тока. К примеру, источник с определенной емкостью имеется электрический провод с живым электрическим кабелем, жилой и металлической кабельной оболочкой.

От чего зависит емкость

Емкость и энергия конденсатора.

Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда конденсатора q одного из проводников к разности потенциалов между проводниками:

Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:

Здесь у нас d – это расстояние между пластинами конденсатора, а q – заряд конденсатора. Подставим эту формулу в выражение для емкости:

Если в качестве диэлектрика у нас выступает воздух, то во всех формулах можно подставить varepsilon = 1.

Для запасенной энергии конденсатора справедливы следующие выражения:

Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.

Итак, мы сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики! Так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку. Не пропустите!

Источник