Изобразим данные, представленные в
таблице, на графике, создав кривую
производственных возможностей.
Существует два определения КПВ, в
каждом из которых содержатся важные
нюансы данной модели:
|
Определение |
|
|
Кривая |
|
Определение |
|
|
Кривая |
Обратим внимание на различия в этих
определениях: первое определяет КПВ
как геометрическое место точек,
отражающих эффективное производство
в нашей экономике, а второе – как границу
всего допустимого производства.
|
ВАЖНЫЙ |
|
|
На кривой производственных возможностей |
Иногда кривую производственных
возможностей называют кривой
трансформации (transformation
curve). Причина этого в том,
что в процессе перехода от одной
альтернативы к другой, скажем, от В к С,
мы как будто «превращаем» одно благо в
другое, переключая ресурсы с производства
блага A на производство
блага B.
|
Обратите |
|
|
На самом деле мы не превращаем благо |
1.4. Форма кривой производственных возможностей
Мы уже выяснили, что КПВ непременно
является убывающей функцией, вследствие
ограниченности ресурсов. Но любая ли
убывающая функция может являться КПВ?
|
1.4.1.
В нашем примере с футбольным матчем |
|
|
Определение |
|
|
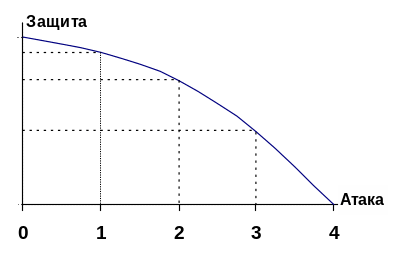
Неоднородные |
|
|
Посмотрим на график. Первыми в атаку |
тяжело
больного, и такой тренер провел бы за
свою карьеру не больше одного матча).
Но аналогично нашему разумному тренеру
поступит и любой другой рационально
мыслящий экономический агент. Сначала
мы включаем в производство самые лучшие
ресурсы, затем – лучшие из оставшихся,
итд.
Пусть
мы хотим последовательно увеличивать
производство одного блага на одну и ту
же величину. Тогда если ресурсы
неоднородны, производство второго блага
будет каждый раз снижаться на все большую
и большую величину, то есть будет
действовать закон возрастания
альтернативных издержек. Поэтому КПВ
будет выпуклой.
|
Обратите |
|
|
КПВ выпуклая, если:
|
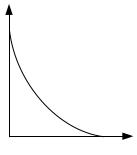
В математике примером уравнения выпуклой
КПВ могут быть уравнения окружности
или эллипса:
A2
= R2 – B2
nA2 = R2
– mB2
|
1.4.2.
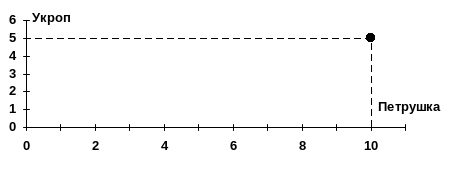
Представьте себе, что у себя на даче |
|
ку, на которой собираетесь
посадить укроп или петрушку. Очевидно,
что на каждом кусочке этой маленькой
грядки (допустим, ее площадь всего 1м2)
укроп будет расти совершенно одинаково.
Причем нам не важно, сколько на этой
грядке может в итоге вырасти петрушки,
а сколько – укропа (в конце концов, мы
изучаем экономику, а не агрономию), но
мы понимаем, что и для петрушки каждый
квадратный сантиметр грядки пригоден
абсолютно одинаково (по крайней мере,
предположим это). В этом случае мы можем
сказать, что наши ресурсы (земля на
грядке, наш труд, садовый инвентарь,
вода для поливки) являются однородными.
|
Определение |
|
|
Однородные |
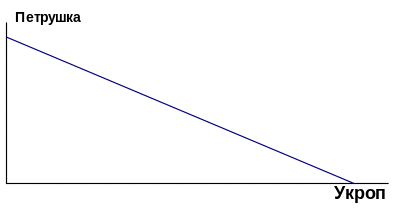
Поэтому мы можем сажать на грядке укроп
и петрушку в любой пропорции, но каждый
раз, одинаково увеличивая
производство укропа, мы будем
пропорционально снижать производство
петрушки.
|
Рассмотрим такую ситуацию на графике:
|
Еще раз отметим, что совершенно не |
|
Обратите |
|
|
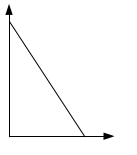
Если ресурсы однородны, КПВ является |
В математике уравнение линейной КПВ
имеет вид линейной функции B
= Bmax – kA, но
график такой функции может располагаться
только в I четверти
координатной плоскости (поскольку
нельзя произвести отрицательное
количество блага).
|
Задача |
|
|
|
Задание 3. Вид КПВ Постройте 1) Весь 2) В 3) В 4) Приближается |
|
1.4.3.
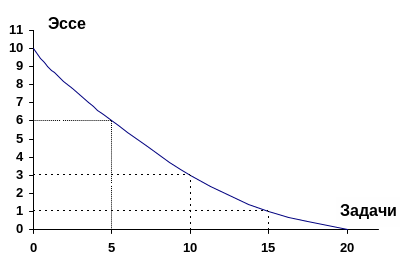
Представьте себе, что вы и ваши |
|
вдруг узнаете, что за
ближайший час вашему классу (всем вместе)
предстоит решить некоторое количество
олимпиадных задач по математике.
Предположим, что в вашем классе 20 человек,
каждый ученик класса может решить за
час одну сложную математическую задачу,
а способности к написанию эссе у всех
различны: пятеро коллективно могут
написать четыре эссе за час, еще пятеро
– три эссе, пятеро следующих напишут
два эссе, а оставшаяся пятерка – одно.
Итого «производственные» возможности
класса составляют 10 эссе за час.
|
Изобразим ваши возможности при помощи |
|
|
|
номисты» и за час вы не напишете |
|
рии – невозможно3. |
|
Обратите |
|
|
В рамках этой темы КПВ считается |
|
1.4.4.
Но вернемся к занятию фермерством |
|
а
арендован у вашей знакомой тетушки
Марфы. На участке есть 10 небольших
грядок, шесть из которых вы можете
использовать как под укроп, так и под
петрушку (они маленькие, то есть ресурсы
однородны). Еще на двух грядках по прихоти
тетушки Марфы можно выращивать только
укроп, а на двух оставшихся участках –
петрушку (вот такая она капризная, ваша
тетушка). Предположим, что на каждой
грядке может вырасти 1 килограмм укропа
или 2 килограмма петрушки. Построим КПВ
для всего участка. Обратите внимание,
что тетушка Марфа не заставляет вас
становиться «счастливым фермером» и
засаживать все грядки, а лишь разрешает
выращивать урожай, то есть на КПВ мы
показываем не результат, а возможности
производства на этом участке.
|
|
Мы можем максимально засеять восемь
|
не прибавится. Этот участок КПВ будет
параллелен оси, на которой отражается
производство укропа (кстати, именно на
этих грядках мы будем сажать укроп в
первую очередь).
-
На
6 грядках мы можем сеять как укроп, так
и петрушку (отказываясь от укропа). КПВ
будет убывающей линией, так как ресурсы
ограничены и (в нашей модели) однородны. -
Еще на двух грядках
мы можем сеять лишь петрушку (или не
сеять ничего). КПВ, иллюстрирующая
производство, здесь будет параллельна
оси, на которой отражается производство
петрушки. И сеять петрушку мы начнем с
этих двух грядок, ведь здесь мы не будем
жертвовать производством укропа.
|
Обратите |
|
|
Участок КПВ параллелен оси блага, если |
|
Задача |
|
|
Задание 3. Уравнение КПВ Постройте |
|
Обратите |
|
|
1. Участок КПВ параллелен оси блага, 2. Вертикальный и |
|
Задача |
|
|
Задание 3. Построение КПВ для Постройте |
1.4.5.
КПВ – точка
|
|
Представим себе, что на следующий год |
Теперь наши ресурсы столь специфичны,
что, снижая производство одного блага,
мы вовсе не получим приращение другого.
|
Обратите |
|
|
КПВ имеет форму точки (является |
|
ВАЖНЫЙ |
|
|
1. Если ресурсы однородны, КПВ – линейная 2. Если 3. Если ресурсы |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
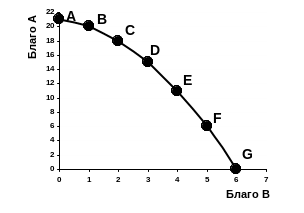
Кривая производственных возможностей
Любая точка на КПВ называется эффективной: она представляет комбинацию благ, при которой невозможно увеличить производство одного блага без соответствующего сокращения производства другого. 
Классификация точек на КПВ
- A — все ресурсы направлены для производства блага Y;
- B — эффективное производство, все ресурсы используются полностью;
- C — эффективное производство, все ресурсы используются полностью;
- D — все ресурсы направлены для производства блага X;
- F — не эффективное производство, не рациональное использование ресурсов. Увеличение одного блага может происходить при увеличении другого, производственные мощности экономической системы не загружены;
- E — недосягаемая для данной экономической системы.
Пути достижения до точки E: 1) интенсивный путь развития (НТП, повышение производительности); 2) экстенсивный путь развития (вовлечение дополнительных ресурсов);
Классификация кривых производственных возможностей 
- нелинейная: выпуклая форма КПВ — закон возрастающих альтернативных издержек (увеличение производства предметов потребления на каждую следующую единицу требует сокращения средств производства на все большую величину). Рисунок 1;
- линейная: увеличение на одну единицу одного блага требует уменьшения на такую же одну единицу второго блага. Полная взаимозаменяемости двух благ. Рисунок 2;
Виды производственных функций:
- Производственная функция Кобба-Дугласа.
- Линейная производственная функция.
- Производственая функция Леонтьева.
Построение кривой производственных возможностей
Закон возрастающих альтернативных издержек
Альтернативные (вмененные) издержки — это количество одного блага, которым необходимо пожертвовать для увеличения производства другого блага.
Альтернативные издержки — ценность лучшего из худших альтернативных способов имеющихся благ (ресурсов).
Движение от точки к точке на КПВ: B => C. Потребление блага X на dX , но теряем потребление блага Y на dY .
dY / dX — альтернативные издержки производства 1 ед. балага X;
dX / dY — альтернативные издержки производства 1 ед. балага Y;
2.1 Кривая производственных возможностей


Определение 1
Кривая производственных возможностей, о которой пойдет речь в данной теме, показывает все возможные комбинации производства различных благ при условии полного и эффективного использования имеющихся ограниченных ресурсов.
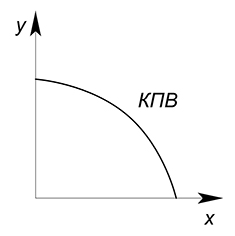 Предпосылки построения КПВ:
Предпосылки построения КПВ:
- В экономике производятся только два вида товаров/услуг;
- В экономике должна применятся самая эффективная технология из всех существующих на данный момент.
Обратимся к графику некоторой КПВ:
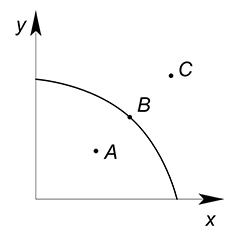
Область, ограниченная графиком КПВ, показывает все доступные нам точки при данном запасе ресурсов и данной технологии.
Рассмотрим $3$ точки:
Точка $A$ лежит под графиком КПВ. Данная точка является неэффективной по Парето (был такой итальянский учёный), потому что можно увеличить объём производства одного блага, не уменьшая количество другого.
Точка $B$ является эффективной по Парето, ибо нельзя увеличить объём производства одного блага, не уменьшая объём производства другого блага.
Точка $C$ является недостижимой при имеющемся количестве ресурсов и данной технологии.
В неэффективную точку можно попасть, если ресурсы используются неэффективно
Функция КПВ
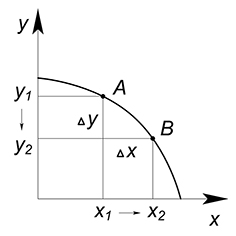
КПВ — невозрастающая функция.
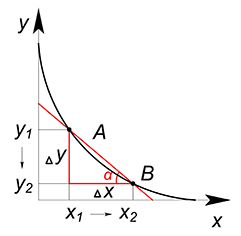
В большинстве случаев КПВ является убывающей функцией. Возьмем произвольную точку $A$, лежащую на графике функции КПВ. В данной точке уже задействованы в производстве товаров $x$ и $y$ все имеющиеся ресурсы. Чтобы увеличить производство товара $x$ ($x_1 to x_2$), нам придётся уменьшить количество производимого товара $y$ ($y_1 to y_2$) (уменьшая объём производства товара $y$, мы освобождаем некоторое количество ресурсов, которые теперь пойдут на производство дополнительных единиц товара $x$). Таким образом, мы имеет положительный прирост аргумента $(x_2-x_1 > 0)$ и отрицательный прирост значения функции $(y_2-y_1 Delta y_1$). Товар может обладать возрастающей альтернативной стоимостью, ибо при увеличении количества одного товара для его производства используются всё менее и менее приспособленные ресурсы. Вогнутость КПВ обусловлена невзаимозаменяемостью ресурсов.
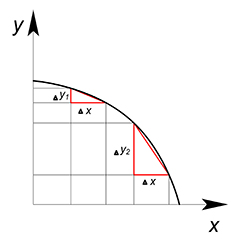 Линейная функция обладает постоянной альтернативной стоимостью на всём своём протяжении. Её альтернативная стоимость вычисляется также как и у вогнутой функции (только работаем мы теперь не с касательной и секущей, а с графиком самой функции). Товар может обладать постоянной альтернативной стоимостью, если ресурсы, необходимые для его производства являются более или менее взаимозаменяемыми.
Линейная функция обладает постоянной альтернативной стоимостью на всём своём протяжении. Её альтернативная стоимость вычисляется также как и у вогнутой функции (только работаем мы теперь не с касательной и секущей, а с графиком самой функции). Товар может обладать постоянной альтернативной стоимостью, если ресурсы, необходимые для его производства являются более или менее взаимозаменяемыми.
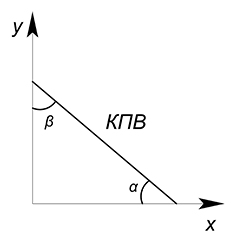
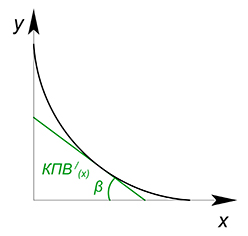
Также нельзя забывать про существование выпуклых функций КПВ. Подобные КПВ обладают убывающей альтернативной стоимостью из-за возрастающей отдачи от масштаба: если мы задействуем в производстве товара много ресурсов, то получается производить его с меньшими издержками. $AC$ данных функций измеряется также, как и любых других, и равна тангенсу угла наклона касательной, проведенной в точку касания при бесконечно делимом $x$ ($AC_x=tgbeta$) или тангенсу угла наклона секущей ($AC_x=tgalpha$) при работе с дискретными величинами.
Ещё существуют КПВ с разной выпуклостью на разных участках.
07. Классификация кривых второго порядка (КВП)
Где A²+ B²+ C² ≠ 0 , называется уравнением кривой второго порядка в прямоугольной системе координат OXY. Преобразуем систему координат таким образом, чтобы уравнение (1) приняло наиболее простой вид.
1. Если в уравнении коэффициент B ≠ 0, то можно повернуть систему координат OXY на угол α такой, что в новой системе координат O’X’Y’ уравнение (1) не будет содержать член с произведением X’Y’.
Действительно, согласно формулам поворота x = x’cosα – y’sinα, y = y’sinα + y’cosα.. Подставляя значения X и Y В (1) легко подсчитать, что коэффициент при X’Y’ примет вид
-2ACosα sinα + B²cos²α — B²sin²α + 2CSinα cosα.
 ,
,
Таким образом, в дальнейшем предполагаем, что уравнение КВП имеет вид
2. Если в уравнении (2) А ≠ 0 и D ≠ 0, либо с ≠ 0 и Е ≠ 0, то, осуществляя параллельный перенос системы координат ОХУ, получаем уравнение КВП, не содержащее член с Х, соответственно У.
Действительно, пусть А ≠ 0, D ≠ 0. Выделим полный квадрат при переменной Х в (2).

Применим формулы параллельного переноса
 ,
,  ,
, 
Тогда уравнение примет вид

Где  . Если же С ≠ 0 и Е ≠ 0, то аналогичным образом исключаем в полученном уравнении член с У.
. Если же С ≠ 0 и Е ≠ 0, то аналогичным образом исключаем в полученном уравнении член с У.
Итак, можно считать, что КВП представляется одним из трёх видов уравнений:
Если – (А/с) › 0 и – (B/C) › 0, то это уравнение эллипса.
Если – (A/C) ‹ 0 b – (B/C) ‹ 0, то получаем пустое множество точек на плоскости.
Аналогичным образом получим гиперболу, вытянутую вдоль оси ОУ.
Если A и B – разных знаков, то всегда можно считать, что А › 0,
Уравнение будет задавать две пересекающиеся прямые Ax  By = 0
By = 0
Если же a и b одного знака, то уравнению удовлетворяет единственная точка О (0,0).
Вывод: любая кривая второго порядка является эллипсом, гиперболой, параболой, парой пересекающихся прямых, парой параллельных прямых, прямой, точкой или пустым множеством.
источники:
http://iloveeconomics.ru/e.conomism/tema-2-alternativnaya-stoimost-krivaya-proizvodstvennyh-vozmozhnostey-poleznost/21
http://matica.org.ua/metodichki-i-knigi-po-matematike/krivye-vtorogo-poriadka/07-klassifikatciia-krivykh-vtorogo-poriadka-kvp

Кривая производственных возможностей
Крива́я произво́дственных возмо́жностей (англ. production possibilities curve) — это кривая, показывающая различные комбинации максимальных объёмов производства нескольких благ (товаров или услуг), которые могут быть созданы в условиях полной занятости при использовании всех имеющихся в экономике ресурсов
Кривая производственных возможностей является частью задачи оптимального распределения ресурсов.
Определение[править | править код]
Согласно К. Р. Макконнеллу и С. Л. Брю кривая производственных возможностей — кривая, демонстрирующая различные комбинации двух товаров или услуг, которые могут быть произведены в условиях полной занятости и полного объёма производства в экономике с постоянными запасами ресурсов и неизменной технологией[1].
Формальное определение[править | править код]
Формальное определение отражает математическую взаимосвязь между различными комбинациями товаров и услуг. Эта зависимость может быть задана уравнением на плоскости:
Вывод[править | править код]
Предположения[править | править код]
Построение кривой производственных возможностей опирается на ряд предположений[1]:
- Экономика эффективна, то есть в экономике достигается полная занятость и полный объём производства.
- Количество и качество ресурсов в экономике постоянно в течение некоторого периода времени.
- Уровень технологий является постоянным.
- Экономика является двухсекторной.
Графический вывод[править | править код]
На графике кривая производственных возможностей обычно представляется выпуклой вверх гладкой линией, полностью лежащей в первой четверти координатной плоскости. На осях отложены количества выпускаемых благ. Точки пересечения с осями соответствуют ситуациям, когда все ресурсы сосредоточены в производстве одного из благ. Выпуклость вверх означает, что ради увеличения производства одного блага на единицу нужно жертвовать все большим количеством второго блага. Тем самым кривая отражает закон убывающей предельной отдачи.
Точки А, Б, В, Г, Д лежат на кривой и отражают различные комбинации выпуска при полном использовании ресурсов. Точка E внутри графика с соответствует неполному (нерациональному) использованию имеющихся ресурсов. Точка Ж над графиком недостижима при заданном количестве ресурсов и имеющемся уровне технологий. Попасть в эту точку можно, если увеличить количество используемых ресурсов или усовершенствовать технологии производства, повысив производительность труда. Например, можно заменить ручной труд на машинный.
Формальный вывод[править | править код]
Кривую производственных возможностей для двухсекторной экономики можно получить формально из следующих предположений.
- Производство каждого товара описывается неоклассической производственной функцией:
.
- Количество капитала в каждом секторе задано :
.
- Уровень технологий не меняется:
.
- Количество труда в целом в экономике задано:
Тогда построение кривой сводится к поиску значений выпуска при различных вариантах использования трудовых ресурсов в экономике. Переток рабочей силы из одного сектора экономики в другой приводит к росту выпуска в первом секторе и падению во втором. Так как предельная отдача труда является убывающей функцией, то изменение выпуска в разных секторах не являются одинаковыми. В первом секторе предельная отдача падает, а во втором растет. Это приводит к тому, что кривая имеет выпуклую (вверх) форму.
Пример формального вывода[править | править код]
Предположим, что количество капитала и уровень технологий в обоих секторах одинаков. Выпуск описывается производственной функций Кобба-Дугласа с одинаковыми параметрами 


Аналогичным образом можно получить границу производственных возможностей для произвольных значений параметров (общей факторной производительности, капитала, параметра производственной функции и т. д.), а также для произвольного количества благ. Для произвольного количества благ граница производственных возможностей будет являться поверхностью (гиперповерхностью) в n-мерном пространстве.
Свойства[править | править код]
Кривая производственных возможностей, или граница производственных возможностей (англ. production possibility frontier (PPF)), или кривая трансформации продукции, представляет собой график сравнения темпов производства двух товаров, на которые используется некоторое ограниченное значение факторов производства. Кривая PPF показывает возможный перечисленный уровень производства одного товара, в результате дающий уровень производства другого. Таким образом можно определить эффективность производства так, чтобы производство одного товара давало максимальный уровень производства другого товара. Период времени обусловлен также и технологиями производства. Товар может быть сопоставлен с благом или услугой.
Кривая производственных возможностей показывает все достижимые комбинации производства продукции, а лежащие вне кривой производственных возможностей, недостижимы из-за редкости ресурсов.
При движении по кривой возможен только один, лучший вариант движения, который дает максимальный результат при минимальных затратах. Кривая производственных возможностей показывает совокупность всех точек или решений, в пределах которых следует выбирать оптимальный вариант. Все остальные точки представляют собой упущенные возможности или альтернативные затраты[1].
Количество других товаров, от которых необходимо отказаться, чтобы получить некоторое количество данного товара, называется альтернативными издержками. Кривая — убывающая, что подразумевает существование альтернативных издержек. Форма кривой производственных возможностей показывает цену одного товара, выраженную в альтернативном количестве другого. Цена КПВ в рыночной экономике — это отражение альтернативной стоимости альтернативных издержек или издержек упущенных возможностей. Она может выражаться в товарах, в деньгах или во времени[1].
Кривая, как правило, изображается как выпуклая вверх («выгнутая») от начала координат, но также может быть представлена как выпуклая вниз или линейная (прямая), в зависимости от ряда факторов. Вогнутость показывает увеличение альтернативных издержек[1].
Практическое применение[править | править код]
Кривая производственных возможностей показывает:
- Тенденции роста альтернативных издержек производства в условиях увеличения производства одного из товаров.
- Уровень эффективности производства.
КПВ может отражать различия в производственных возможностях разных стран.
Кривая может быть использована для представления ряда экономических понятий, таких как нехватка ресурсов, альтернативные издержки, эффективность производства, эффективность распределения ресурсов, а также экономии за счёт масштабов. Кроме того, внешнее смещение кривой — результат роста доступности ресурсов, таких как физический капитал, рабочая сила и технический прогресс наших знаний. С другой стороны, кривая будет смещаться внутрь, если сокращается рабочая сила, запасы исходного сырья исчерпываются или стихийное бедствие уменьшит запас физического капитала. Комбинация представляет собой точку на кривой, где экономика работ показывает приоритеты или выбор экономики, как выбор между производством большего числа товаров производственного назначения и меньшего товаров народного потребления, или наоборот.
Согласно К. Р. Макконнеллу и С. Л. Брю возможными областями практического применения кривой производственных возможностей являются[1]:
- использование в качестве микроэкономического инструмента в части бюджетного ограничения, набора альтернативных возможностей;
- в части анализа производственных возможностей в критические периоды, например перед вступлением в войну и во время войны, когда необходимо увеличить производство при уже достигнутой полной занятости;
- при анализе различных дискриминаций, когда их устранение придаёт существенный прирост экономики;
- в части инструмента при выборе взаимоисключающих альтернатив, например сохранения окружающей среды и увеличения вредного производства;
- в части инструментария при анализе увеличения производительности труда, когда необходимо выбрать текущий уровень инвестиций за счет снижения текущего уровня потребления;
- использование во внешнеторговом анализе, когда страна за счёт внешней торговли имеет возможность достичь уровень выше своей границы производственной возможности и создания торгового дефицита;
- использование в качестве инструментария в экологической экономике, анализ последствий смещения кривой производственных возможностей влево;
- при анализе наложения торгового эмбарго на страну, и анализ последствий смещения кривой производственных возможностей влево.
Эффективность[править | править код]
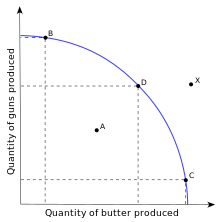
An example PPF with illustrative points marked
Кривая показывает все возможные комбинации нескольких товаров, которые могут быть произведены одновременно в течение определённого периода времени, при прочих равных условиях. Как правило, она принимает форму кривой, показанной на рисунке справа. Для экономики, при увеличении количества одного произведённого товара, производство другого товара должно быть уменьшено. Так, производство сливочного масла должно быть сокращено для того, чтобы производить больше оружия. Кривые показывают, какова зависимость между уменьшением объёмов последнего производства и увеличением первого, и наоборот.
Примечания[править | править код]
- ↑ 1 2 3 4 5 6 Макконнелл К. Р., Брю С. Л. Экономикс: принципы, проблемы и политика : [рус.] = Economics: Principles, Problems, and Policies. — М. : Республика, 1992. — Т. 1. — С. 39—41, 45-47. — ISBN 5-250-01486-0.
Иван может получить на своем поле либо 400 т пшеницы, либо 1000 т картофеля. Для Петра альтернативной стоимостью выращивания одной тонны картофеля будет производство 0,25 т пшеницы при максимальном урожае картофеля, равном 1200 т. Два фермера – Иван и Петр – решили объединить свои усилия. Это не увеличит их производительности.
а) Построить кривую производственных возможностей «коллективного» хозяйства.
б) Верно ли, что альтернативной стоимостью производства первых 1200 т картофеля является производство 400 т пшеницы?
в) Верно ли, нельзя произвести 600 т картофеля и 550 т пшеницы?
г) Верно ли, что при производстве 1700 т картофеля альтернативной стоимостью увеличения производства картофеля на 20 т является отказ от 8 т пшеницы?
д) Верно ли, что для увеличения производства пшеницы с 200 т на 550 т нужно пожертвовать снижением урожая картофеля на 1100 т.
Решение:
а) Кривая производственных возможностей – это кривая, каждая точка которой показывает все возможные сочетания максимального производства двух экономических благ, в условиях полной занятости ресурсов и неизменной технологии.
Найдём координаты точек перелома:
А: Максимальное производство пшеницы обоих фермеров – 700 тонн. На поле Ивана можно вырастить 400 тонн, на поле Петра – 300 тонн:
1200 × 0,25 = 300.
При этом объём картофеля будет нулевым.
В: Далее определим, на каком из двух полей следует начать выращивать картофель, если фермер решит выращивать хотя бы небольшое его количество.
Для этой цели выберем из двух полей то, на котором выращивание каждой единицы картофеля приведёт к наименьшим потерям объёма пшеницы. То есть выберем то поле, где альтернативные издержки выращивания картофеля наименьшие.
На поле Ивана альтернативные издержки 1 т картофеля равны 0,4 т пшеницы.
А на поле Петра альтернативные издержки 1 т картофеля равны 0,25 т пшеницы.
0,25 меньше чем 0,4, значит, для производства первых тонн картофеля выгоднее использовать поле Петра.
Максимально на его поле можно вырастить 1200 т картофеля, пожертвовав при этом 300 тонн пшеницы.
Точка В будет иметь координаты: 1200 тонн картофеля, 400 тонн пшеницы.
С: Максимальное количество картофеля, которое можно вырастить на двух полях равно 2200 тонн (1000 тонн на поле Ивана и 1200 тонн на поле Петра). При этом объём пшеницы будет нулевым.
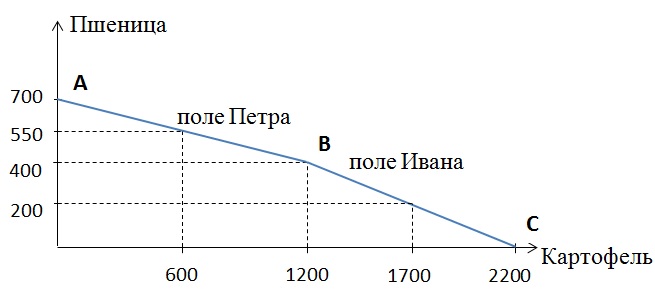
б) Неверно, так как альтернативной стоимостью производства первых 1200 т картофеля является производство 300 т пшеницы.
в) Точка, в которой производится 600 тонн картофеля, соответствует верхнему участку КПВ, отражающему производственные возможности поля Петра.
КПВ поля Петра является линейной функцией вида:
Y = a – b × X,
где а – максимально возможный объём пшеницы, когда все ресурсы используются только в производстве пшеницы,
b – коэффициент, характеризующий наклон КПВ и отражающий величину альтернативных издержек выращивания 1 т картофеля.
Итак, КПВ поля Петра описывается уравнением:
Y = 700 – 0,25 × X,
При производстве 600 тонн картофеля можно максимально вырастить:
Y = 700 – 0,25 × 600 = 550 тонн пшеницы.
Таким образом, можно произвести 600 т картофеля и 550 т пшеницы.
г) Точка, в которой производится 1700 т картофеля соответствует нижнему участку КПВ, отражающему производственные возможности поля Ивана.
На поле его поле альтернативные издержки 1 т картофеля равны 0,4 т пшеницы.
Альтернативной стоимостью увеличения производства картофеля на 20 т является отказ от 8 т пшеницы:
8 / 20 = 0,4 т пшеницы – верно.
д) Да, это так.
1700 – 600 = 1100
Как известно, главной проблемой экономики является удовлетворение (а точнее его невозможность) безграничных человеческих потребностей в условиях ограниченности располагаемых ресурсов. Ограниченное количество имеющихся у нас ресурсов позволяет произвести конечное количество благ и услуг.
Определение 1
Кривая производственных возможностей, о которой пойдет речь в данной теме, показывает все возможные комбинации производства различных благ при условии полного и эффективного использования имеющихся ограниченных ресурсов.
 Предпосылки построения КПВ:
Предпосылки построения КПВ:
- В экономике производятся только два вида товаров/услуг;
- В экономике должна применятся самая эффективная технология из всех существующих на данный момент.
Обратимся к графику некоторой КПВ:

Область, ограниченная графиком КПВ, показывает все доступные нам точки при данном запасе ресурсов и данной технологии.
Рассмотрим $3$ точки:
Точка $A$ лежит под графиком КПВ. Данная точка является неэффективной по Парето (был такой итальянский учёный), потому что можно увеличить объём производства одного блага, не уменьшая количество другого.
Точка $B$ является эффективной по Парето, ибо нельзя увеличить объём производства одного блага, не уменьшая объём производства другого блага.
Точка $C$ является недостижимой при имеющемся количестве ресурсов и данной технологии.
В неэффективную точку можно попасть, если ресурсы используются неэффективно
Функция КПВ

КПВ – невозрастающая функция.
В большинстве случаев КПВ является убывающей функцией. Возьмем произвольную точку $A$, лежащую на графике функции КПВ. В данной точке уже задействованы в производстве товаров $x$ и $y$ все имеющиеся ресурсы. Чтобы увеличить производство товара $x$ ($x_1 to x_2$), нам придётся уменьшить количество производимого товара $y$ ($y_1 to y_2$) (уменьшая объём производства товара $y$, мы освобождаем некоторое количество ресурсов, которые теперь пойдут на производство дополнительных единиц товара $x$). Таким образом, мы имеет положительный прирост аргумента $(x_2-x_1 > 0)$ и отрицательный прирост значения функции $(y_2-y_1<0)$. Большему значению аргумента соответствует меньшее значение функции, следовательно, данная функция является убывающей.
Альтернативная стоимость и КПВ
Определение 2
Альтернативная стоимость показывает от какого количества единиц другого блага (например, блага $y$) нужно отказаться для производства одной дополнительной единицы первого блага (например, блага $x$)
Геометрический смысл альтернативной стоимости
Наиболее часто встречающимися графиками КПВ являются линейная и вогнутая функции.
Разберем геометрический смысл $AC$ на примере вогнутой функции:
Если мы работаем с дискретными величинами, прирост $x$ и прирост $y$ являются целыми числами, альтернативная стоимость дополнительной единицы $x$ равна $dfrac{Delta y}{Delta x}=tgalpha$, то есть тангенсу угла наклона секущей. (Деля $Delta y$ на $Delta x$ мы ищем сколько единиц товара $y$ приходится на дополнительную единицу товара $x$).
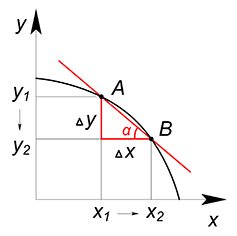
Но во многих экономических задачах товары считаются бесконечно делимыми. В таком случае нам нужно посчитать то количество товара $y$ от которого нам пришлось отказаться, чтобы произвести дополнительное бесконечно малое количество товара $x$. В данной ситуации альтернативная стоимость товара $x$ в некоторой точке $A$ (АС приращения $x_A$ на бесконечно малую величину) – это угол наклона касательной в этой точке, то есть производная функции КПВ.
Подробнее о производных и секущих вы можете узнать здесь.
Закон, актуальный для вогнутых функций:
При увеличении объёмов производства товара его альтернативная стоимость растет ($Delta y_2>Delta y_1$). Товар может обладать возрастающей альтернативной стоимостью, ибо при увеличении количества одного товара для его производства используются всё менее и менее приспособленные ресурсы. Вогнутость КПВ обусловлена невзаимозаменяемостью ресурсов.
 Линейная функция обладает постоянной альтернативной стоимостью на всём своём протяжении. Её альтернативная стоимость вычисляется также как и у вогнутой функции (только работаем мы теперь не с касательной и секущей, а с графиком самой функции). Товар может обладать постоянной альтернативной стоимостью, если ресурсы, необходимые для его производства являются более или менее взаимозаменяемыми.
Линейная функция обладает постоянной альтернативной стоимостью на всём своём протяжении. Её альтернативная стоимость вычисляется также как и у вогнутой функции (только работаем мы теперь не с касательной и секущей, а с графиком самой функции). Товар может обладать постоянной альтернативной стоимостью, если ресурсы, необходимые для его производства являются более или менее взаимозаменяемыми.
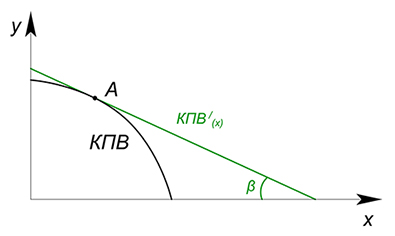
$AC_x=tgalpha$
$AC_y=tgbeta$

Также нельзя забывать про существование выпуклых функций КПВ. Подобные КПВ обладают убывающей альтернативной стоимостью из-за возрастающей отдачи от масштаба: если мы задействуем в производстве товара много ресурсов, то получается производить его с меньшими издержками. $AC$ данных функций измеряется также, как и любых других, и равна тангенсу угла наклона касательной, проведенной в точку касания при бесконечно делимом $x$ ($AC_x=tgbeta$) или тангенсу угла наклона секущей ($AC_x=tgalpha$) при работе с дискретными величинами.


Ещё существуют КПВ с разной выпуклостью на разных участках.