Кенгуру как найти число

Кенгуру как найти число

  1. Главная
  3. Олимпиада по математике
  5. Разборы задач Олимпиад по математике
  7. Разбор заданий конкурса Кенгуру по математике. 18 марта 2021. 7 класс

Решения:

Задача 1
Правильный ответ: В

Диагональ разбила четырехугольник на два треугольника, у которых она является общей стороной. Для сторон треугольника должно выполняться неравенство: сумма двух, даже самых маленьких сторон, должна быть больше третьей. Подбираем возможные варианты. Из предложенных чисел можно составить только два треугольника: один – со сторонами 1, 2, 2,8, а другой – 2,8; 5; 7,5. Общей стороной является сторона длиной 2,8 – значит, это и есть искомая диагональ.

Задача 2
Правильный ответ: А

Ось симметрии есть только у одного из этих знаков – это Стрелец. Она совпадает с центральной линией «стрелки». Остальные приведенные знаки симметрией не обладают

Задача 3
Правильный ответ: Д

Фиксируем вертикальный диаметр, и серый цвет из фигур справа от диаметра переносим в равные им фигуры слева от диаметра. Закрасится полкруга, 50%

Задача 4
Правильный ответ: Б

Строим их, начиная с самого маленького: 1234, 2345, 3456, 4567, 5678, 6789. Всего 6.

Задача 5
Правильный ответ: А

Складывая паззл, получим пример 2–102. Ответ: -100

Задача 6
Правильный ответ: Б

Складываем столбиком, опираясь на решенный верно пример для двухзначных чисел, или используя сумму разрядных слагаемых. Ясно, что В+D=7 или 17, а А+С=13 или 12. Для суммы четырехзначных чисел получится: 1000∙(А+С)+100∙(В+D)+10∙(С+А)+1∙(В+D) = 1000∙13+100∙7+10∙13+1∙7=13837. Для второго варианта ответ тот же.

Задача 7
Правильный ответ: Б

По условию каждое колесико поворачивается на половину оборота. На колесике цифры: 0 и 5, 1 и 6, 2 и 7, 3 и 8, 4 и 9 — будут находиться диаметрально противоположно. Поэтому для ответа выбираем диаметрально противоположные цифры для 6348. Получим число 1893. Это вариант Б.

Задача 8
Правильный ответ: Д

Достаточно изобразить отрезками рост мальчиков, и ответ будет ясен.
Другой вариант: пусть рост Антона — х, тогда Бори – (х+5), Вани – (х+15), Гриши – (х+25), Димы – (х+30). Значит Дима выше Антона (или Антон ниже Димы, как предложено в ответах) на 30 см.

Решения:

Задача 9
Правильный ответ: Г

Согласно условию, одна сторона шоколадки содержит 6 квадратов (12÷2=6) а другая 11 квадратов (9+2=11). Ясно, что отламывали от шоколадки с разных сторон плитки. Всего в плитке 11∙6=66 квадратов. Съели 12+9=21 квадрат, тогда осталось 66-21=45 квадратов.

Задача 10
Правильный ответ: Д

Пусть вес банки равен х, а вес воды в полной банке у.
Тогда по условию имеем: (х+ 4/5у)–(х+ 1/5у)=740–560.
Отсюда находим у — вес воды в банке (у), он равен 300 г.
Теперь по первому условию получаем: 560–300÷5=500 г – вес пустой банки.

Задача 11
Правильный ответ: В

Согласно условию, сторона большого квадрата будет равна 4 см (т.к. площадь равна 16 кв.см). Находим площадь белого треугольника. Его основание будет равно 2 см, и высота тоже 2. По формуле площадь одного такого треугольника равна 2 кв.см, а площади четырех таких треугольников — 8 кв.см. Тогда площадь черных фигур – это площадь большого квадрата минус площади четырех серых квадратов и четырех белых треугольников. 16–8–4=4 кв.см.

Задача 12
Правильный ответ: В

Обозначим сторону самого большого квадрата как у. Тогда сторона нижнего левого квадрата будет иметь длину (у-1), сторона верхнего левого – длину (у-2), а верхнего справа от него – длину (у-3). Используя это выражение, получим, что длина самого большого квадрата может быть записана как (у-4)+h. Но она же у нас была принята за у.
Получаем: (у-4)+h=у. Отсюда находим, что h=4.
Разбор заданий конкурса Кенгуру по математике. 18 марта 2021. 7 класс

Задача 13
Правильный ответ: Б

Пусть х – количество вопросов с правильными ответами, у – с неправильными, z – вопросы без ответов.
Тогда имеем: х+у+z =20, 7х–4у=100. Тогда 7х=100+4у.
Подбираем у, учитывая, что 100+4у кратно 7. Подходит у=3. В этом случае х=(100+4∙3)÷7=16, а z=20-3-16=1.
Отметим, что также подходит у=10, но в этом случае х=20, не соответствует условию (всего 20 вопросов). Значит ответ: 1 вопрос остался без ответа.

Задача 14
Правильный ответ: В

У прямоугольника с площадью Р стороны равны х и 4, значит Р=4х. Стороны треугольника с углом 450 равны между собой и равны 4 см, и этот треугольник является половиной квадрата со стороной 4 и площадью 16 (т.к в этом месте лист согнут в два слоя). Площадь Q в 2 раза меньше площади Р и будет равна 4х÷2=2х. Площадь всего прямоугольника равна 13∙4=52. Тогда получаем: 4х+2х+16=52. Отсюда находим, что х=6.

Задача 15
Правильный ответ: Д

Пусть в корзине лежит 2А яблок, и такое же количество фруктов получила Кристи. Пусть у нее х яблок, тогда груш (2А–х). Лили получила А фруктов, у нее яблок (2А–х), и их количество равно количеству груш у Кристи.

Задача 16
Правильный ответ: В

Данная дробь — а/b. Новая дробь, которую получили увеличением числителя на 40% — 1,4а/хb и она вдвое больше исходной.
Получим: 2а/b=1,4а/хb.
Отсюда 2ахb=1,4аb. Получаем, что х=0,7.
Это означает, что х=70% от b. Значит, знаменатель b уменьшили на 30%

Решения:

Задача 17
Правильный ответ: Г

Вершина пирамиды – D. Второй ряд содержит ядра с буквами А,В,С. Третий ряд – ядра с буквами В,Е,D,С,Е,А. Четвертый ряд – D,Е,С,А,Е,В,С,В,А и невидимое ядро с неизвестной буквой. Так как каждая буква должна присутствовать на 4 ядрах, то проверяем и находим, что не достает метки D.

Задача 18
Правильный ответ: Б

Число 1ABCDE умножаем на 3 столбиком. При умножении Е на 3 на конце 1, значит, Е=7, запоминаем 2.
D умножаем на 3 и прибавляем 2, на конце 7, значит, D=5, запоминаем 1.
С умножаем на 3 и прибавляем 1, на конце 5, значит, С=8, запоминаем 1.
В умножаем на 3 и прибавляем 2, на конце 8, значит, В=2
А умножаем на 3, на конце стоит 2, значит, А=4, запоминаем 1.
1 умножаем на 3 прибавляем 1, получим 4 – это А.
Все сошлось. Число 142857. Сумма его цифр равна 27.

Задача 19
Правильный ответ: Б

Задача на принцип Дирихле. Сумму всех фишек примем за х. Тогда наименьшее количество фишек каждого цвета будет равняться:
х–26 = зеленые
х–24 = красные
х–21 = синие
х–16 = желтые.
Складывая, получим уравнение: 4х–87=х, откуда получаем, что х=29 – наименьшее количество фишек.

Задача 20
Правильный ответ: Г

10 шестиугольников на видимой части мяча и столько же на невидимой. Всего 20.

Задача 21
Правильный ответ: Г

Возможны два случая отбора для образования пар: один случай — 20 рыцарей и 2000 лжецов, второй случай – 21 рыцарь и 1999 лжецов.
Рассмотрим первый вариант: 20 рыцарей и 2000 лжецов. Возможно три варианта пар: (лжец, лжец) – пусть х пар, (лжец, рыцарь) = (2000–2х÷у) – у пар по количеству рыцарей, которые вошли в эту пару; (рыцарь, рыцарь) – (20–у) ÷2 пар.
Первая пара назовет рыцарями 2х человек, лжецами никого; вторая пара назовет лжецами (2000–2х+у) человек, рыцарями никого; третья пара назовет рыцарями (20–у) человек, лжецами никого.
Всего 1010 пар, 20 человек названы лжецами и 2000 человек названы рыцарями, составляем уравнения:
х+у+(20–у)÷2 = 1010
2х+20–у=2000
2000–2х+у=20.
Решая их, получим х=995 – столько было пар лжецов.
Второй случай не подойдет, так как х получится не целым числом, что противоречит условию.

Задача 22
Правильный ответ: В

Соединим точку К со всеми вершинами четырехугольника, тогда образуется 8 треугольников. Будем сравнивать их площади, применяя свойство площадей треугольников: площади треугольников, у которых высота одинаковая, относятся как основания. Площадь треугольника МКВ (см. рисунок в первом комментарии) примем за х, а площадь треугольника ВКР за у. На рисунке указаны площади других треугольников, выраженные через х и у. Нужно найти (х+у). Используя четырехугольник с площадью 18, получим уравнение: 6+2у+2х=18, откуда х+у=6.

Разбор заданий конкурса Кенгуру по математике. 18 марта 2021. 7 класс

Задача 23
Правильный ответ: Б

Считаем окрашенные грани. Они будут у 8 кубиков в вершинах и у 3 кубиков на одном ребре, кроме тех, которые образуют вершины. Итого на всех ребрах получится 3∙12=36 кубиков. Внутри каждой грани останется 9 покрашенных кубиков, которые не в вершинах и не на сторонах. Тогда во всех гранях 9∙6=54 кубика. Складываем и получаем общее количество интересующих нас кубиков: 8+36+54=98.

Задача 24
Правильный ответ: Г

Точка пересечения вершин всех треугольников является общей вершиной 5 равных углов, сумма которых 360 градусов. Тогда один угол равен 360÷5=72 градуса. Другой острый угол треугольников будет равен 90-72=18 градусов. Чтобы построить звезду нужно 360÷18=20 треугольников.

Источник

Перейти к содержимому

Всем известная олимпиада Кенгуру претерпела некоторые изменения и превратилась в 3 олимпиады для разных возрастных групп.

ИГРА «СМАРТИК» для первоклассников 25-28 января 2022 1 класс smartik.org
КОНКУРС-ИГРА «Смарт КЕНГУРУ» 25 января 2022 2-10 классы mathkang.ru
ТЕСТИРОВАНИЕ «Смарт ЕГЭ» 25-28 января 2022 11 класс mathkang.ru

Кенгуру 2022

Кенгуру 2022 — математика для всех

Математический конкурс «Кенгуру» проходит ежегодно и является одним, пожалуй, самым популярным в мире. В нем принимают участи около 6 миллионов школьников, 2 миллиона которых из РФ. Каждый, желающий может проверить свои силы и принять участие. Сложность заданий зависит возраста участников. Различают задания для 2 класса, для 3 и 4, для 5 и 6, для 7 и 8, для 9 и 10 классов.

Содержание статьи

  • Кенгуру 2022
  • Задания и ответы олимпиады Кенгуру прошлых лет

Кенгуру 2022

С 25 января 2022 года начнется игра «Смартик», конкурс-игра «Смарт КЕНГУРУ» и тестирование «Смарт ЕГЭ». Подведение итогов игры «Смартик» и тестирования «Смарт ЕГЭ» будет происходить до конца марта, а вот итоги конкур-игры Смарт КЕНГУРУ будут подводиться до конца учебного года. Всем участникам вручается сертификат, в котором указывается место по стране, району и школе. Кроме того, победителям и призёрам вручаются ценные призы. В данном разделе вы сможете ознакомиться с конкурсными заданиями за предыдущие годы.

Задания и ответы олимпиады «Кенгуру» за прошлые годы

2021: 2 класс, 3-4 класс, 5-6 класс, 7-8 класс, 9-10 класс
2020: 2 класс, 3-4 класс, 5-6 класс, 7-8 класс, 9-10 класс

2019 год
 2 класс  3-4 класс 5-6 класс
7-8 класс  9-10 класс
2018 год
 2 класс  3-4 класс 5-6 класс
 7-8 класс  9-10 класс
2017 год
 2 класс  3-4 класс 5-6 класс
7-8 класс  9-10 класс
2016 год
 2 класс  3-4 класс 5-6 класс
7-8 класс  9-10 класс
2015 год
 2 класс 3-4 класс 5-6 класс
7-8 класс  9-10 класс
2014 год
 2 класс  3-4 класс 5-6 класс
7-8 класс  9-10 класс
2013 год
 2 класс  3-4 класс 6-7 класс
7-8 класс  9-10 класс
2012 год
 2-3 класс  4-5 класс 6-7 класс
7-8 класс  9-10 класс

Источник

Кенгуру 2023 ответы

Согласно Правилам международного комитета конкурса Кенгуру, публикация заданий и решений до 16 апреля категорически запрещена

Содержание

  1. Кенгуру ответы 1-2 класс
  2. Кенгуру ответы 3-4 класс
  3. Кенгуру ответы 5-6 класс
  4. Кенгуру ответы 7-8 класс
  5. Кенгуру ответы 9-11 класс

Кенгуру ответы 1-2 класс

  • Сколько кругов изображено на рисунке?

Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: 8

  • Кенгуру построили фигуру из пяти кубиков. Как Выглядит эта фигура, если смотреть на нее сверху?

Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: Б

  • Имеется пять стеклянных ваз. В какой лежат шары с написанными на них номерами. В какой вазе сумма чисел на всех шарах наибольшая?

Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: А

  • Миша разрезал квадрат так. как показано на рисунке 1. Из получившихся кусочков он составил фигуру (рисунок 2). Какой из кусочков Миша не использовал, когда составлял фигуру?

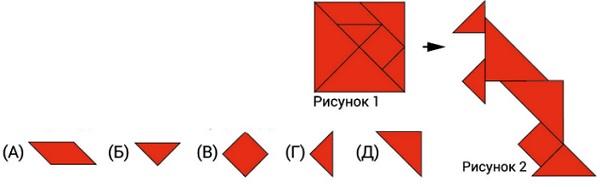
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: А

  • Петя нарисовал кораблик. На его кораблике нарисовано больше одного круга. Треугольников на нём на 2 больше, чем квадратов. Какой из корабликов нарисовал Петя?

Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: Д

  • На каком рисунке фигуры не являются отражением друг друга относительно пунктирной линии?

Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: Б

  • На день рождения дедушке преподнесли торт со свечками, обозначающими возраст именинника. Большая тёмная свечка означает 10 лет, а маленькая светлая — 1 год. Сколько лет исполнилось дедушке?

Ответ:

  • Водитель едет из точки А в точку Б. На каждом перекрёстке они отмечены красными кружками он делает остановку, а затем двигается дальше, не меняя направления. Сколько раз он остановится на пути от точки А до точки Б.

Ответ:

  • В парке растёт 5 деревьев. Юля может видеть только два из них, так как они загораживают ей остальные деревья. В какой точке находится Юля?

Ответ:

  • В верном равенстве два одинаковых числа были закрыты квадратиками со знаками вопроса. Какие числа были закрыты?

Ответ:

  • Люся нарисовала таблицу размером 5*6 ячеек. Сначала она закрасила все ячейки в третьей и шестой строках, а затем все ячейки в третьем и четвёртом столбцах. Сколько ячеек осталось не закрашено?

Ответ: 16 ячеек

  • Лист бумаги сложили пополам и вырезали в нём два отверстия: квадратное и круглое (смотри рисунок). Как будет выглядеть лист, когда его развернут обратно?

Ответ:

  • Улитка ползёт в гости к подруге 3 часа, если нет дождя. Если идёт дождь, она ползёт в 2 раза быстрее. Во сколько улитка окажется в гостях, если она выползла ровно в 9 часов утра, а ровно в 10 часов пошёл дождь?

Ответ: в 11 часов

Кенгуру ответы 3-4 класс

  • У Вани было пять одинаковых свечей. Он зажёг их одновременно, а затем погасил каждую в своё время. После этого свечи стали выглядеть так, как показано на рисунке. Какую свечу Ваня потушил первой?

Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: D

  • В верном равенстве два одинаковых числа были закрыты квадратами со 20+10+10+?+?+1=51 знаками вопроса. Какие числа были закрыты?

Ответ: 5

  • Диск с двумя отверстиями накладывают на циферблат часов и вращают вокруг центра. Какую ещё пару чисел можно увидеть одновременно?

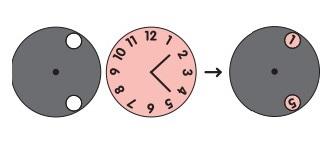
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: 5 и 9

  • У Алисы есть четыре кусочка пазла. Какие два кусочка она должна сложить вместе, чтобы получить полный квадрат?

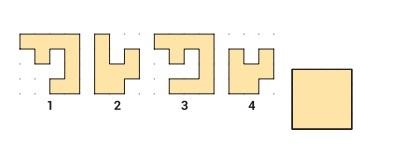
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: 1 и 4

  • Светотехник в театре включает цветные прожекторы по такому плану. В течение первой минуты светит только синий прожектор. В последние две минуты светят жёлтый и синий прожекторы. Суммарно в течение скольких минут светят ровно два прожектора одновременно?

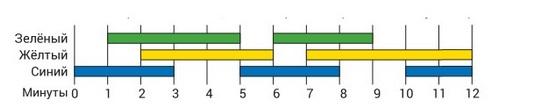
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: 8 минут

  • Костя сложил лист прозрачной плёнки по пунктирной линии, как показано на рисунке. Какое изображение он увидел?

Ответ:

  • У Аллы есть четыре диска разных размеров. Она хочет построить такую башню из трёх дисков, где каждый следующий диск меньше, чем предыдущий. Сколько различных вариантов таких башен Алла может построить?

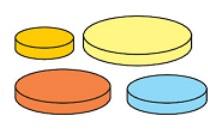
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: 4

  • Дима наклеил два кусочка бумаги поверх круга. Какую из изображённых фигур он не мог получить?

Ответ:

  • Фигуру на рисунке можно составить из пяти элементов. Какой из этих элементов должен содержать точку?

Ответ:

  • Имеется шесть гирь массой 1, 2, 3, 4, 5 и 6 кг. Пять их них поставили на весы так, как показано на рисунке. При этом одна гиря осталась в стороне. Весы пришли в равновесие. Какая гиря осталась в стороне?

Ответ:

  • У Юры есть линейка длиной 60 см. Некоторые из делений на ней стёрлись. Несмотря на это, он может измерить любую из длин 10, 20, 30 ,40, 50 и 60 см, используя свою линейку только один раз. Какая из следующих линеек принадлежит Юре?

Ответ:

  • На светофоре стоят 8 машин. В каждой машине находится 2 или 3 человека. Всего в этих машинах 19 человек. В скольких автомобилях находится ровно 2 человека?

Ответ:

  • Севернее дороги А расположено 7 домов, южнее дороги А- 5 домов, восточнее дороги В — 8 домов. Сколько домов расположено западнее дороги B?

Ответ:

  • На Линии метро имеется 6 станций: A, B C D E F. Поезд останавливается на каждой станции. Когда он прибывает на конечную станцию, он разворачивается и движется в обратном направлении. Водитель поезда начал движение на станции B, и его первая остановка была на станции C. На какой станции будет его 96-я остановка?

Ответ:

Кенгуру ответы 5-6 класс

  • Валера заполняет таблицу числами от 1 до 40 подряд, как показано на рисунке. Какой кусочек он сможет вырезать из таблицы, когда заполнит её до конца?

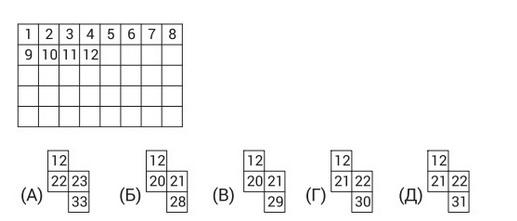
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: В

  • Кенгуру составляет числа из спичек. Цифры от 0 до 9 он всегда составляет так, как показано на рисунке. Например, чтобы составить таким способом число 15 или 8, ему потребуется семь спичек. Какое наибольшее положительное число кенгуру может составить из семи спичек?

Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: 711

  • У Иры есть развёртка, из которой она складывает кубик. Какой из следующих пяти кубиков у неё получился из этой развёртки?

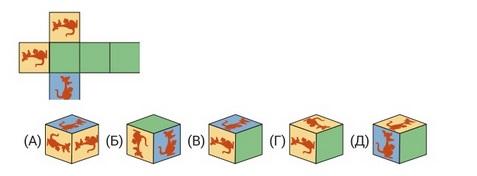
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: Б

  • Альпинист взбирается по цилиндрической башне снизу вверх. Его путь отмечен на рисунке чёрным цветом. Все шаги альпиниста одинакового размера. Девять шагов видны на изображении. Сколько его шагов не видны?

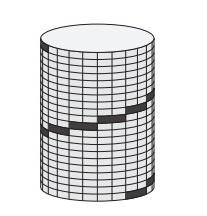
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: 12

  • У Саши есть пять дисков разных размеров. Он хочет построить такую башню из четырёх дисков, где каждый следующий диск меньше, чем предыдущий. Сколько различных вариантов таких башен Саша может построить?

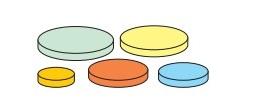
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: 5

Кенгуру ответы 7-8 класс

  • Решётка на рисунке состоит из вертикальных и горизонтальных линий. Одна часть этой решётки была скрыта. Какой из следующих кусочков является скрытой частью решётки?

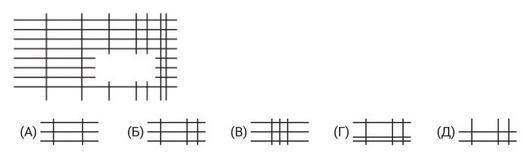
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: Б

  • Какую из следующих фигур нельзя разделить на две трапеции одной прямой линией?

Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: А

  • Диск с двумя отверстиями наложен на циферблат часов так, как показано на рисунке. Диск вращают вокруг центра до тех пор, пока в одном из отверстий не появится цифра 8. Какие два других числа возможно увидеть одновременно с ней?

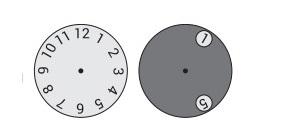
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: 4 или 12

  • Коля хочет расставить по одному числу в каждой вершине ромба так, чтобы число, написанное на ребре, равнялось сумме двух чисел в вершинах, которые это ребро соединяет. Какое число должно стоять на месте вопросительного знака?

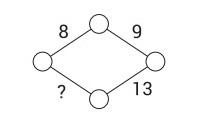
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: 12

  • У Кристины есть кусок прозрачной плёнки с нарисованными на ней линиями. Она складывает его пополам, как показано на рисунке. Что она увидит?

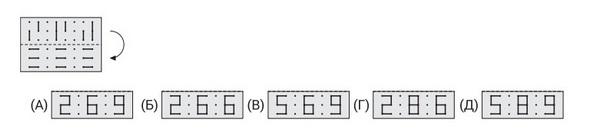
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: В

  • Мастер хочет выложить плиткой пол, используя плитки только одной формы. Зазоры и пропуски не допускаются. Плитка какой формы не может быть использована?

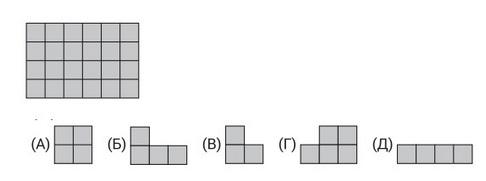
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: Г

  • У Жени имеется 150 монет. Когда она бросила их на стол, 40% из них легли орлом вверх, и 60% — решкой вверх. Сколько монет, упавших решкой вверх, ей нужно перевернуть, чтобы количество монет, лежащих орлом вверх, и количество монет, лежащих решкой вверх, стало равным?

Ответ: 15

Кенгуру ответы 9-11 класс

  • По дороге в школу Маше пришлось бежать, чтобы успеть на автобус. Через две остановки она вышла и пошла дальше пешком. Какой из следующих графиков зависимости скорости от времени лучше всего представляет её дорогу до школы?

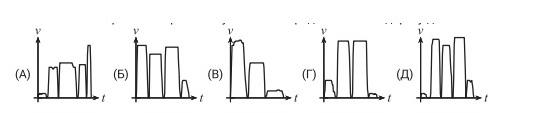
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: Г

  • Целые положительные числа m и n являются нечётными. Какое из следующих целых чисел также является нечётным?

Ответ: mn+2

  • Внутри большого квадрата со стороной 10 см расположен меньший квадрат со стороной 4 см (смотри рисунок). Соответствующие стороны двух квадратов параллельны, и их центры совпадают. Какой процент площади большого квадрата закрашен серым цветом?

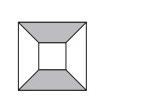
Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: 42%

  • Сегодня четверг. Какой день недели будет через 2023 дня?

Ответ: четверг

  • Прямоугольник ABCD составлен из 30 одинаковых квадратов. Периметр закрашенной фигуры равен 240 см. Чему равна площадь прямоугольника ABCD?

Кенгуру 2023 ответы на тестирование Кенгуру – выпускникам

Ответ: 1920 см2

  • Семья состоит из пяти человек. Сумма их возрастов — 80 лет. Двум самым младшим членам этой семьи — 6 и 8 лет. Какова была сумма возрастов членов этой семьи 7 лет назад?

Ответ: 46

  • Деревянный забор состоит из ряда вертикальных досок, каждая из которых соединена со следующей четырьмя горизонтальными досками. Первая и последняя доски в заборе вертикальные. Какое из следующих чисел может быть общим количеством досок в заборе?

Ответ: 96

  • В выражении a/5=7/b буквы a и b заменяют целыми положительными числами так, чтобы равенство было верным. Сколькими различными способами это может быть сделано?

Ответ: 1

  • После того как Вся выиграл 200 партий в шахматы, процент его побед составил 49%. Какое наименьшее количество дополнительных игр ему нужно выиграть, чтобы увеличить процент побед до 50%?

Ответ: Г

  • В каждой вершине треугольной пирамиде записано по целому положительному числу, а на каждом ребре указана сумма двух чисел, записанных в вершинах, которое это ребро соединяет. Какое число должно стоять на месте знака вопроса?

Ответ: Д

  • Женя решила экономить воду. Она сократила время, в течение которого умывается, на четверть. Она так же снизила напор воды, чтобы на четверть уменьшить скорость ее вытекания из крана. На какую долю Женя уменьшила общее количество воды, которое она использует для умывания?

Ответ: 3/8

  • На рисунке изображены три квадрата со сторонами 3 см, 5 см, 8 см. Какова площадь закрашенной фигуры?

Ответ: 55/4^2

  • Провод длиной 95 м разрезали на 3 части так, чтобы длина каждого следующего куска была на 50% больше, чем длина предыдущего. Какова длина самого большого куска провода?

Ответ: 45 м.

  • М и N – середины двух противоположных сторон прямоугольника. Какая часть прямоугольника закрашена?

Ответ: 1/4

  • У исследователя есть два сплава: первый сплав содержит 90% золота, а второй 54% золота. Он смешал 320 граммов первого и 160 граммов второго сплава, получив третий сплав. Сколько процентов золота содержится в получившимся сплаве?

Ответ: 78%

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 мая 2022 года; проверки требует 1 правка.

В вычислительной теории чисел[en] и вычислительной алгебре алгоритм «кенгуру» Полларда (а также лямбда-алгоритм Полларда, см. раздел «Название» ниже) — это алгоритм решения задачи дискретного логарифмирования. Алгоритм был предложен в 1978 специалистом в области теории чисел Дж. М. Поллардом[en] в той же статье[1], что и его более известный ρ-алгоритм для решения той же задачи. Хотя Поллард описывает применение этого алгоритма для задачи дискретного логарифмирования в мультипликативной группе по модулю простого p, он является, фактически, общим алгоритмом дискретного логарифмирования — он будет работать на любой циклической конечной группе.

Алгоритм[править | править код]

Пусть G — конечная циклическая группа порядка n, генерируемая элементом alpha , и мы ищем дискретный логарифм x элемента beta по основанию alpha . Другими словами, мы ищем {displaystyle xin Z_{n}}, такое, что {displaystyle alpha ^{x}=beta }. Лямбда-алгоритм позволяет нам искать x в некотором подмножестве {displaystyle {a,ldots ,b}subset Z_{n}}. Мы можем искать полный набор возможных логарифмов, приняв a=0 и {displaystyle b=n-1}, хотя в этом случае ρ-алгоритм будет эффективнее. Поступаем следующим образом:

1. Выбираем множество S целых чисел и определяем псевдослучайное отображение[en] {displaystyle f:Grightarrow S}.

2. Выберем целое число N и вычислим последовательность элементов группы {displaystyle {x_{0},x_{1},ldots ,x_{N}}} согласно формулам:

3. Вычислим

{displaystyle d=sum _{i=0}^{N-1}f(x_{i})}.

Заметим, что

{displaystyle x_{N}=x_{0}alpha ^{d}=alpha ^{b+d},.}

4. Начинаем вычислять вторую последовательность элементов группы {displaystyle {y_{0},y_{1},ldots }} по формулам

и соответствующую последовательность целых чисел согласно формуле

{displaystyle d_{n}=sum _{i=0}^{n-1}f(y_{i})}.

Заметим, что

{displaystyle y_{i}=y_{0}alpha ^{d_{i}}=beta alpha ^{d_{i}}} для {displaystyle i=0,1,ldots ,N-1}

5. Прекращаем вычисления {displaystyle {y_{i}}} и {displaystyle {d_{i}}}, когда выполняется одно из условий

A) {displaystyle y_{j}=x_{N}} для некоторого j. Если последовательности {x_i} и {displaystyle {y_{j}}} «сталкиваются» таким способом, мы имеем:

{displaystyle x_{N}=y_{j}Rightarrow alpha ^{b+d}=beta alpha ^{d_{j}}Rightarrow beta =alpha ^{b+d-d_{j}}{pmod {n}}Rightarrow xequiv b+d-d_{j}{pmod {n-1}}}
так что мы нашли требуемое.
B) {displaystyle d_{i}>b-a+d}. Если это случилось, алгоритм потерпел неудачу в поиске x. Может быть сделана другая попытка путём изменения множества S или/и отображения f.

Сложность[править | править код]

Поллард указал для алгоритма временную сложность {displaystyle {scriptstyle O({sqrt {b-a}})}}, основываясь на вероятностной аргументации, что вытекает из предположения, что f действует псевдослучайно. Заметим, что в случае, когда размер множества {a, …, b} измеряется а битах, что обычно в теории сложности, множество имеет размер log(b − a), так что алгоритмическая сложность равна {displaystyle {scriptstyle O({sqrt {b-a}})=O(2^{{frac {1}{2}}log(b-a)})}}, что является экспонентой от размера задачи. По этой причине лямбда-алгоритм Полларда считается алгоритмом экспоненциальной сложности. За примером подэкспоненциального по времени алгоритма см. Алгоритм исчисления порядка.

Название[править | править код]

Алгоритм известен под двумя названиями.

Первое название — алгоритм «кенгуру» Полларда. Имя относится к аналогии, используемой в статье, где алгоритм был предложен. В статье алгоритм объясняется в терминах использования ручного кенгуру для поимки дикого. Как объяснял Поллард[2], эта аналогия была навеяна «обворожительной» статьёй, опубликованной в том же выпуске журнала Scientific American, что и публикация RSA криптосистемы с открытым ключом. Статья[3] описывает эксперимент, в котором «энергетическая цена движения кенгуру, измеренная в терминах потребления кислорода на различных скоростях, была определена путём помещения кенгуру на беговую дорожку».

Второе название — лямбда-алгоритм Полларда. Очень похоже на имя другого алгоритма Полларда для дискретного логарифмирования, ρ-алгоритма, и это имя связано с похожестью визуализации алгоритма с греческой буквой лямбда (lambda ). Короткая линия буквы лямбда соответствует последовательности {x_i}. Соответственно, длинная линия соответствует последовательности {displaystyle {y_{i}}}, которая «сталкивается с» первой последовательностью (подобно встрече короткой и длинной линии буквы).

Поллард предпочитает использование названия «алгоритм кенгуру»[4], чтобы избежать путнаницы с некоторыми параллельными версиями ρ-алгоритма, которые тоже носят название «лямбда-алгоритмы».

См. также[править | править код]

  • Радужная таблица

Примечания[править | править код]

  1. ↑ Pollard, 1978.
  2. ↑ Pollard, 2000, с. 437—447.
  3. ↑ Dawson, 1977, с. 78—89.
  4. ↑ jmptidcott2. Дата обращения: 5 ноября 2016. Архивировано 17 августа 2016 года.

Литература[править | править код]

  • J. Pollard. Monte Carlo methods for index computation mod p // Mathematics of Computation. — 1978. — Т. 32.
  • J. Pollard. Kangaroos, Monopoly and Discrete Logarithms // Journal of Cryptology. — 2000. — Т. 13. — С. 437—447.
  • T. J. Dawson. Kangaroos // Scientific American. — 1977. — С. 78—89.
Источник

Перейти к содержимому

Официальная олимпиада-игра Смарт - Кенгуру 3-4 класс по математике 2023 (задания и ответы) Олимпиаду по математике Кенгуру пишут школьники по всей России. Ниже предоставлены официальные задания и ответы для игры «СМАРТ КЕНГУРУ». Официально олимпиаду пишут 31 января

Смотреть полные официальные задания и ответы: Перейти

Некоторые задания и решения

1. Смартик сложил из одинаковых палочек число 2023 два раза. На сколько палочек больше он использовал во второй раз?
Ответ: В

2. Смартик придумал шифр: если число находится в круге — это означает, что к нему прибавляется 5, а если в квадрате, то вычитается 4. Какое число зашифровано на рисунке?
Ответ: Г

3. В ряду 10 стульев. Маша села на седьмой стул справа, а Лена — на седьмой стул слева. Сколько стульев между ними?
Ответ: Б

4. В точке О находится колодец. Из какой точки нельзя добраться до колодца, двигаясь по дорожкам?
Ответ: В

5. Коала Клара обозначает сотни кругами, десятки — квадратами и единицы — треугольниками. Она сосчитала листья на своем эвкалипте. Результат её подсчётов изображен на рисунке. Сколько листьев на эвкалипте?
Ответ: Б

6. Уроки в школе начинаются в 9 часов. В 8 часов 45 минут Петя был на полпути от дома до школы. Если он будет идти с той же скоростью, то придёт в школу за 10 минут до уроков. Сколько минут занимает у него весь путь от дома до школы?
Ответ: А

7. Два одинаковых квадратных листа бумаги наложили друг на друга. После этого, не смещая листы, сделали два разреза по пунктирным линиям, как показано на рисунке. Сколько частей получилось?
Ответ: Г

8. Какое утверждение про число 999 неверно?
Ответ: Д

Вам будет интересно:

Кенгуру и Смарт Кенгуру — математический конкурс 2022-2023 (задания и ответы)

* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР

Поделиться:

Источник

Добавить комментарий