Нахождение радиуса круга: формула и примеры
В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.
Формулы вычисления радиуса круга

1. Через длину окружности/периметр круга
Радиус круга/окружности рассчитывается по формуле:

C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:
C = 2 π R
π – число, приближенное значение которого равно 3,14.
2. Через площадь круга
Радиус круга/окружности вычисляется таким образом:

S – это площадь круга; равна числу π , умноженному на квадрат его радиуса:
S = π R 2
Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
Радиус — что это такое и как найти радиус окружности
Через длину стороны

Формула для нахождения длины окружности через радиус:
, где r — радиус окружности.
Найти радиус круга, зная окружность
Окружность круга P
Результат

Радиус и диаметр
Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.

Обозначается диаметр также первой буквой своего слова – D или d.
Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.
Длина диаметра равна удвоенной длине радиуса.

Вычисление радиуса
Радиус можно посчитать разными способами.
Если известен диаметр
Этот способ самый простой. Диаметр равен двум радиусам. Поэтому радиус будет высчитываться по формуле r=d/2.
Если известна длина окружности круга
Также несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.
Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так:

Означает данное значение отношение длины окружности к диаметру той же окружности.
Если известна площадь круга
Формула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса:

В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса.
Как найти радиус круга, все школьники учат на геометрии. Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок.
Способ расчета радиуса круга:

Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга: 
где P – длина окружности, pi – число π, равное примерно 3.14

Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга: 
где S – площадь круга, pi – число π, равное примерно 3.14
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Как посчитать радиус зная длину окружности
Чему равен радиус (r) если длина окружности C?
Формула
r = C /2π , где π ≈ 3.14
Свойства радиуса
В отношении радиуса действуют несколько важных правил:
- Радиус составляет половину диаметра. Это мы продемонстрировали только что.
- У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.


Радиус, который перпендикулярен хорде, делит ее на две равные части.
Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.

По площади сектора и центральному углу


- Например, если площадь сектора равна 50 см 2 , а центральный угол равен 120 градусов, формула запишется следующим образом: .




Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла .

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах , получаем



В случае, когда величина α выражена в в радианах , получаем



Формулы для площади круга и его частей
 ,
,
где R – радиус круга, D – диаметр круга
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |  |
| Площадь круга |
 |
 ,
,
где R – радиус круга, D – диаметр круга
Площадь сектора

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь сегмента

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Центральный угол, вписанный угол и их свойства
Связанные определения
- Центральный угол в окружности — это угол , образованный двумя радиусами.
- Радиус кривизны кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.
Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла .

В случае, когда величина α выражена в градусах , справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах , справедлива пропорция

из которой вытекает равенство:

Уравнение окружности
r 2 = ( x – a ) 2 + ( y – b ) 2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:
| < | x = a + r cos t |
| y = b + r sin t |
Углы между двумя хордами
Случай 1: два секущие пересекаются внутри окружности.

Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны Случай 2: две секущие пересекаются вне окружности.
Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Основные свойства касательных к окружности

3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
Обобщения
Радиусом множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, радиус n-размерного гиперкуба со стороной s равен
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.

- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Площадь круга, онлайн расчет
Как найти площадь круга по формуле через радиус либо диаметр круга.
Площадь круга, онлайн расчет
Вместо заключения
Чтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так.

Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности. А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.
Круг. Окружность (центр, радиус, диаметр)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

Данный урок посвящён изучению окружности и круга. Также учитель научит отличать замкнутые и незамкнутые линии. Вы познакомитесь с основными свойствами окружности: центром, радиусом и диаметром. Выучите их определения. Научитесь определять радиус, если известен диаметр, и наоборот.
[spoiler title=”источники:”]
http://exceltut.ru/radius-chto-eto-takoe-i-kak-najti-radius-okruzhnosti/
http://interneturok.ru/lesson/matematika/3-klass/tema-umnozhenie-i-delenie/krug-okruzhnost-tsentr-radius-diametr
[/spoiler]
Как найти радиус круга, диаметр и длину окружности – формула, решение задач
В этом онлайн уроке рассказывается о том, как найти радиус круга, диаметр и длину окружности – формула, решение задач. По всей видимости, круг является одной из самых главных геометрических фигур нашей вселенной. Достаточно всего лишь посмотреть на форму орбит планет, или то, что можно увидеть на молекулярном уровне. Круг встречается в нашей жизни постоянно. На этом занятии речь пойдет об основных свойствах и параметрах круга. В простом понимании круг представляет собой множество точек, одинаково удаленных от центра. Расстояние от точки до центра круга называется радиусом. Величина, которая характеризует ширину круга, т.е. максимальное расстояние между точками круга, называется диаметром. Диаметр равен по длине двум радиусам и это понятно из определения. Расстояние по границе круга называется длиной окружности. В этом видео уроке будет изучена формула для нахождения длины окружности по радиусу. Здесь также рассмотрено несколько примеров с решением задач по этой теме. Видео урок «Как найти радиус круга, диаметр и длину окружности – формула, решение задач» вы можете смотреть онлайн совершенно бесплатно в любое время. Успехов!
- Длительность: 11:00
- Рейтинг: 0.0/0
- 1
- 2
- 3
- 4
- 5
Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.
Как найти радиус окружности
Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.
Выбирайте формулу в зависимости от известных величин.
Через площадь круга
- Разделите площадь круга на число пи.
- Найдите корень из результата.
- R — искомый радиус окружности.
- S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
Через длину окружности
- Умножьте число пи на два.
- Разделите длину окружности на результат.
- R — искомый радиус окружности.
- P — длина окружности (периметр круга).
- π (пи) — константа, равная 3,14.
Через диаметр окружности
Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.
- R — искомый радиус окружности.
- D — диаметр.
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника
- Перемножьте три стороны треугольника.
- Разделите результат на четыре площади треугольника.
- R — искомый радиус окружности.
- a, b, с — стороны вписанного треугольника.
- S — площадь треугольника.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Через площадь сектора и его центральный угол
- Умножьте площадь сектора на 360 градусов.
- Разделите результат на произведение пи и центрального угла.
- Найдите корень из полученного числа.
- R — искомый радиус окружности.
- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Через сторону вписанного правильного многоугольника
- Разделите 180 градусов на количество сторон многоугольника.
- Найдите синус полученного числа.
- Умножьте результат на два.
- Разделите сторону многоугольника на результат всех предыдущих действий.
- R — искомый радиус окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✂️📌
- Как найти периметр прямоугольника
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
Содержание:
- § 1 Понятие окружности и дуги
- § 2 Радиус окружности
- § 3 Диаметр окружности и хорда
§ 1 Понятие окружности и дуги
В этом уроке Вы познакомитесь с такими понятиями, как окружность и круг, узнаете, что такое дуга, радиус, диаметр и хорда окружности.
Итак, начнем с определения, что же такое окружность?
Окружность – это геометрическая фигура на плоскости, все точки которой равноудалены от данной точки – центра окружности. Обычно центр окружности принято обозначать точкой О.

Как можно построить окружность? С помощью циркуля!
Ножку с иголкой устанавливают в точку О – центр окружности, а ножка с грифелем опишет замкнутую линию, которую и называют окружностью.
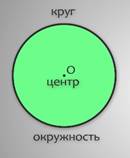
Любая окружность разделяет плоскость на 2 части. Ту часть плоскости, которая лежит внутри окружности вместе с самой окружностью, называют кругом. Точка О является как центром окружности, так и центром круга.
Таким образом, нетрудно заметить, что геометрическая фигура круг имеет площадь, а окружность нет, она имеет только длину, так как является замкнутой линией.
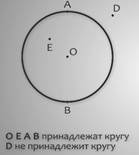
Как Вы догадались, точки могут лежать на окружности, т.е. мы будем говорить, принадлежать окружности, а могут и не лежать на ней, т.е. не принадлежать окружности. Например, точки А и В принадлежат окружности с центром в точке О; точки О, Е и D не принадлежат окружности с центром в точке О; точки О, Е, А, В принадлежат кругу с центром в точке О, а точка D не принадлежит этому кругу. Точки А и В делят окружность на две части, каждую из которых называют дугой окружности; ну а сами точки А и В – концами дуг. Значит, дуга – это часть окружности, ограниченная двумя точками.
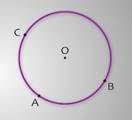
Давайте выполним следующее задание: назовите дуги, на которые делят окружность точки А, В и С.
Решение: давайте сначала назовем дуги с концами в точках А и В: это дуга АВ, а вторая дуга АСВ, мы ее назвали по трем точкам, чтобы различать их, теперь назовем дуги с концами в точках В и С: дуга ВС, дуга ВАС, ну и остались дуги с концами в точках А и С: дуга АС, дуга АВС.
§ 2 Радиус окружности
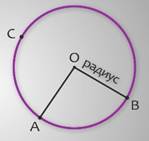
На рисунке вы видите, что отрезки ОА и ОВ соединяют центр окружности с точками, лежащими на окружности. Их называют радиусами. Таким образом, радиус – это отрезок, соединяющий центр окружности с одной из её точек. Радиусы принято обозначать латинской буквой R или r. В каждой окружности все радиусы равны между собой!
А как вы думаете, сколько радиусов можно провести в одной окружности? Бесконечное множество!
§ 3 Диаметр окружности и хорда
А теперь давайте выполним следующие построения: начертим окружность с центром в точке О и радиусом 3 см.
Это значит надо при помощи линейки раствор циркуля сделать равным трем сантиметрам, ножку с иголкой поместить в точку О, а ножкой с грифелем описать окружность.
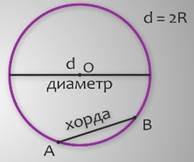
Затем, отметим на данной окружности две точки – А и В. Соединим их отрезком, получили хорду АВ. То есть, отрезок, соединяющий две точки окружности, называют хордой. Кстати, самую большую хорду, ту, которая проходит через центр окружности, называют диаметром. Диаметр принято обозначать латинскими буквами d или D. Между прочим, диаметр равен удвоенному радиусу, пишут d = 2R. Диаметр делит круг на два полукруга, а окружность – на две полуокружности.
Таким образом, в этом уроке Вы узнали, что такое окружность и круг, научились их строить, а также познакомились с таким понятиями как дуга, радиус, диаметр и хорда окружности.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. – М: 2013.
- Дидактические материалы по математике 5 класс. Автор – Попов М.А. – 2013 год
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор – Минаева С.С. – 2014 год
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. – 2010 год
- Контрольные и самостоятельные работы по математике 5 класс. Авторы – Попов М.А. – 2012 год
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009.
Окружность радиус диаметр видеоурок

Математика 3 класс (Урок№33 – Круг. Окружность (центр, радиус, диаметр)

Что такое круг окружность радиус

